1.1 What is Mathematics?
Figure it out (Page 2):
1. Can you think of other examples where mathematics helps us in our everyday lives?
Answer:
Some examples where mathematics helps us in our everyday lives are:
(i) Mathematics helps us in counting things such as money.
(ii) Mathematics helps us when deciding how and where to invest our money.
(iii) It helps us in calculating sizes of objects.
(iv) It helps us calculating distances and time taken to cover the distances.
(v) When sharing an item among several people, maths helps us decide how much of the item to give to each person.
(vi) To determine the quantity of food required to serve a certain number of guests.
(vii) When buying items from the store, we need mathematics to find the best deals and discounts
(viii) To determine whether your electricity bill is accurate.
(ix) To calculate the number of balls of wool required to knit a sweater.
(x) Maths helps us determine how fast an object is moving.
(xi) To determine the quantity of paint is required to paint a house.
2. How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Answer:
Mathematics has helped propel humanity forward in the following ways:
(i) It has helped us build roads, highways and flyovers.
(ii) It has helped us engineer many different forms of transport such as cars, buses, trains (including modern bullet trains), aeroplanes etc.
(iii) It has helped us engineer computers (including supercomputers) and computer programs such as the internet.
(iv) It has helped us tackle cybercrime by helping us implement next-generation security measures.
(v) It has helped us build smartphones and smartphone applications.
(vi) Mathematics has played an essential role in building complex navigation systems.
(vii) Maths has also played a huge role in developing medicines and other technology which have helped cure complex diseases.
1.2 Patterns in Numbers
Figure it out (Page 3):

1. Can you recognize the pattern in each of the sequences in Table 1?
Answer:
| Number Sequences | Pattern Description |
| 1, 1, 1, 1, 1, 1, 1, … (All 1’s) | Each number in the sequence is 1. |
| 1, 2, 3, 4, 5, 6, 7, … (Counting numbers) | Each number in the sequence is 1 more than the previous number, starting from 1. |
| 1, 3, 5, 7, 9, 11, 13, … (Odd numbers) | Each number in the sequence is 2 more than the previous number, starting from 1. |
| 2, 4, 6, 8, 10, 12, 14, … (Even numbers) | Each number in the sequence is 2 more than the previous number, starting from 2. |
| 1, 3, 6, 10, 15, 21, 28, … (Triangular numbers) | Triangular numbers are numbers you get by adding up dots to form a triangle: 1, 3 (1+2), 6 (1+2+3), 10 (1+2+3+4), and so on! |
| 1, 4, 9, 16, 25, 36, 49, … (Squares) | Numbers in the sequence are squares of consecutive numbers, starting from 1. |
| 1, 8, 27, 64, 125, 216, … (Cubes) | Numbers in the sequence are cubes of consecutive numbers, starting from 1. |
| 1, 2, 3, 5, 8, 13, 21, … (Virahānka numbers) | Each number in the sequence is obtained by adding the preceding two numbers. |
| 1, 2, 4, 8, 16, 32, 64, … (Powers of 2) | This series shows numbers that keep doubling each time, starting from 1. |
| 1, 3, 9, 27, 81, 243, 729, … (Powers of 3) | Numbers in the sequence are obtained by multiplying each preceding number by 3. |
2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Answer:
(i) 1, 1, 1, 1, 1, 1, 1, …
The next three numbers in the sequence are 1, 1, 1.
Rule: Each number in the sequence is = 1.
(ii) 1, 2, 3, 4, 5, 6, 7, …
The next three numbers in the sequence are 8, 9, 10.
Rule: Each number in the sequence is 1 more than the previous number, starting from 1.
(iii) 1, 3, 5, 7, 9, 11, 13, …
The next three numbers in the sequence are 15, 17, 19.
Rule: Each number in the sequence is 2 more than the previous number, starting from 1.
(iv) 2, 4, 6, 8, 10, 12, 14, …
The next three numbers in the sequence are 16, 18, 20.
Rule: Each number in the sequence is 2 more than the previous number, starting from 2.
(v) 1, 3, 6, 10, 15, 21, 28, …
The next three numbers in the sequence are 36, 45, 55.
Rule: You get eachnumber by progressively adding consecutive numbers starting from 1.
1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10 etc.
(vi) 1, 4, 9, 16, 25, 36, 49, …
The next three numbers in the sequence are 64, 81, 100.
Rule: Numbers in the sequence are obtained by multiplying consecutive numbers, starting from 1, by themselves.
(vii) 1, 8, 27, 64, 125, 216, …
The next three numbers in the sequence are 343, 512, 729.
Rule: Numbers in the sequence are obtained by multiplying consecutive numbers, starting from 1, by themselves twice.
(viii) 1, 2, 3, 5, 8, 13, 21, …
The next three numbers in the sequence are 34, 55, 89.
Rule: Each number in the sequence is obtained by adding the preceding two numbers.
(ix) 1, 2, 4, 8, 16, 32, 64, …
The next three numbers in the sequence are 128, 256, 512.
Rule: This series shows numbers that keep doubling each time, starting from 1.
(x) 1, 3, 9, 27, 81, 243, 729, …
The next three numbers in the sequence are 2187, 6561, 19683.
Rule: Numbers in the sequence are obtained by multiplying each preceding number by 3.
1.3 Visualising Number Sequences
Figure it out (Page 5):
1. Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!
Answer:
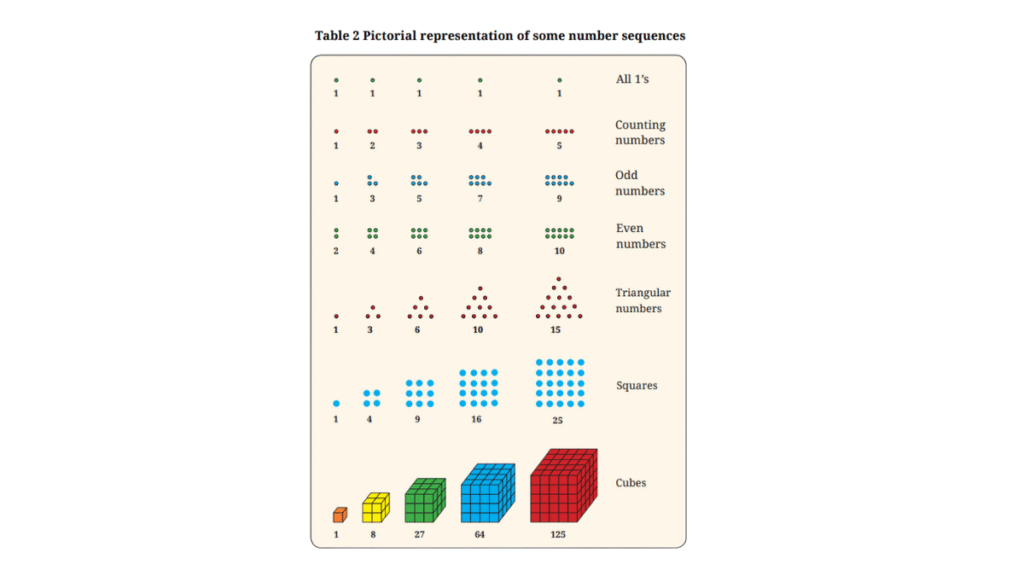
The next picture in each sequence is shown below:

2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?
Answer:
1, 3, 6, 10, 15, … are called triangular numbers because they can be arranged as dots in the form of equilateral triangles.
1, 4, 9, 16, 25, … called square numbers or squares because they can be arranged as dots in the form of squares.
1, 8, 27, 64, 125, … called cubes because they can be arranged in the form of cubes.
3. You will have noticed that 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures in your notebook illustrating this!
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
Number 36:

Number 16:

Number 28:

4. What would you call the following sequence of numbers?
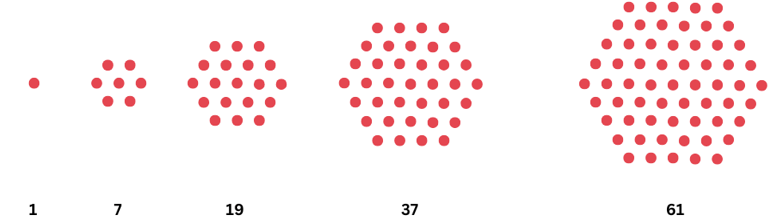
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Answer:
The hexagonal numbers are drawn below:

The next number in the series is 61 as shown below:

5. Can you think of pictorial ways to visualise the sequence of Powers of 2? Powers of 3?
Here is one possible way of thinking about Powers of 2:
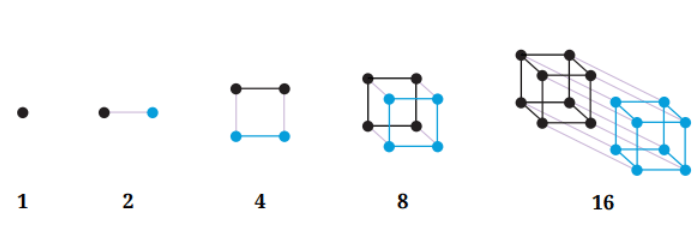
Answer:
Powers of 3:
1.4 Relations among Number Sequences
Figure it out (Page 8):
1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?
Answer:
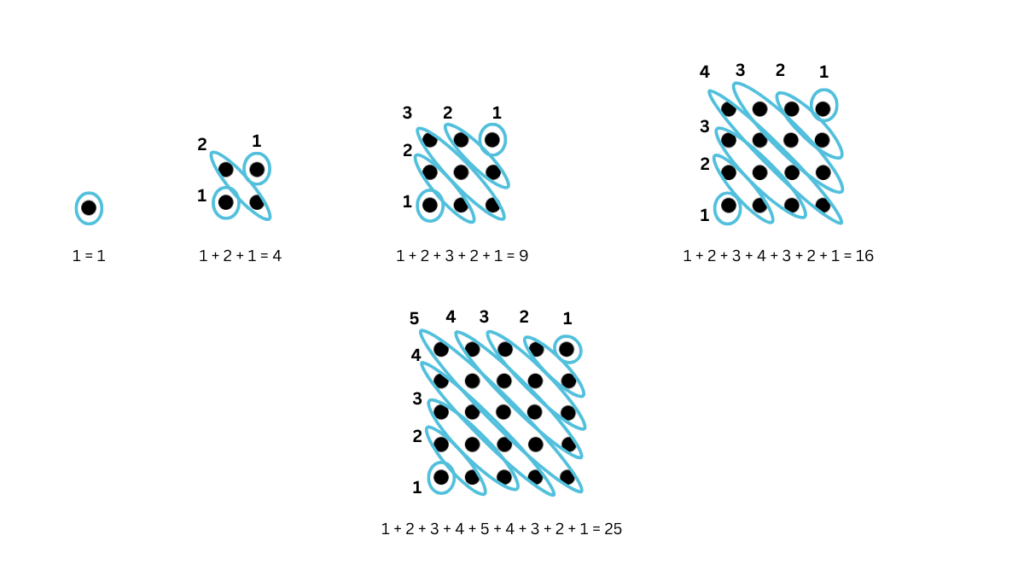
2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1?
Answer:
Let us observe the pattern below:
The sequence (1 + 2 + 1) forms a square with side length = 2.
The sequence (1 + 2 + 3 + 2 + 1) forms a square with side length = 3.
The sequence (1 + 2 + 3 + 4 + 3 + 2 + 1) forms a square with side length = 4.
The sequence (1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1) forms a square with side length = 5.
Similarly, the sequence (1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1) forms a square with side length = 100.
Therefore, the sum of (1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1) = 100 × 100 = 10000.
3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?
Answer:
The All 1’s sequence is as follows: (1, 1, 1, 1, ….).
Adding the All 1’s sequence up:
1 = 1
1 + 1 = 2
1 + 1 + 1 = 3
1 + 1 + 1 + 1 = 4
Therefore, we get the Counting numbers sequence (1, 2, 3, 4, ….)
Adding the All 1’s sequence up and down:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
Therefore, we get the Squares number sequence.
4. Which sequence do you get when you start to add the Counting numbers up? Can you give a smaller pictorial explanation?
Answer:
Counting numbers are as follows: (1, 2, 3, 4, 5, …..)
When we start to add the Counting numbers up we get:
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
We get Triangular numbers (1, 3, 6, 10, …)
A pictorial explanation is shown below:

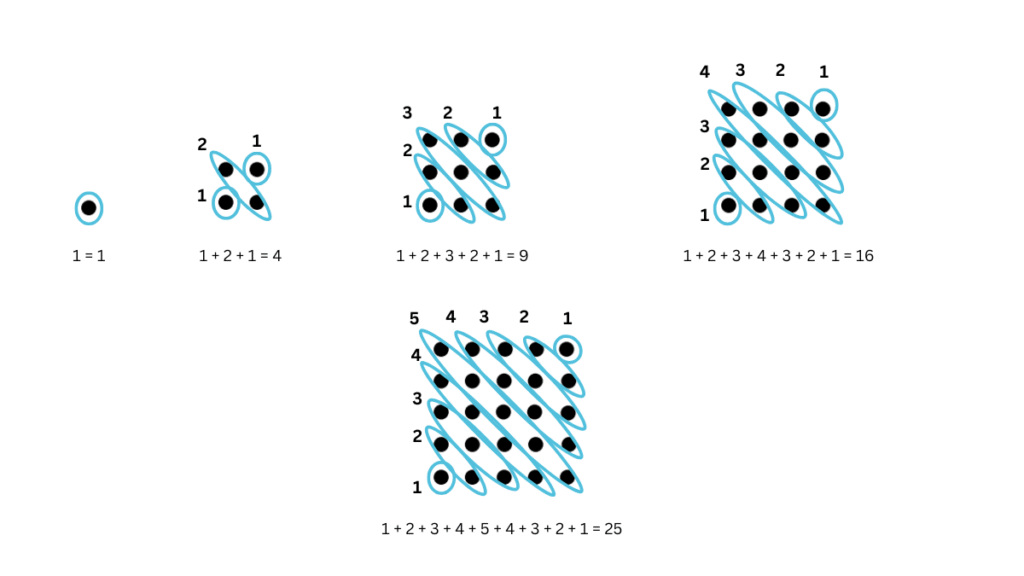
5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, ….? Which sequence do you get? Why? Can you explain it with a picture?
Answer:
1 + 3 = 4
3 + 6 = 9
6 + 10 = 16
10 + 15 = 25
6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, ….? Now add 1 to each of these numbers—what numbers do you get? Why does this happen?
Answer:
We get,
1 = 1
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
The sequence is (1, 3, 7, 15, …)
Adding 1 to each of these numbers we get,
1 + 1 = 2
1 + 3 = 4
1 + 7 = 8
1 + 15 = 16
The sequence is (2, 4, 8, 16, …), which can also be written as (21, 22, 23, 24, ….).
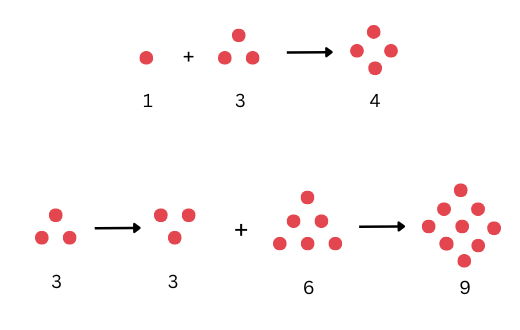
7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Answer:
Triangular numbers:
1, 3, 6, 10, 15, …
Multiplying by 6 and adding 1:
1 × 6 + 1, 3 × 6 + 1, 6 × 6 + 1, 10 × 6 + 1, 15 × 6 + 1, …
= 7, 19, 37, 61, 91
The sequence is Hexagonal numbers.
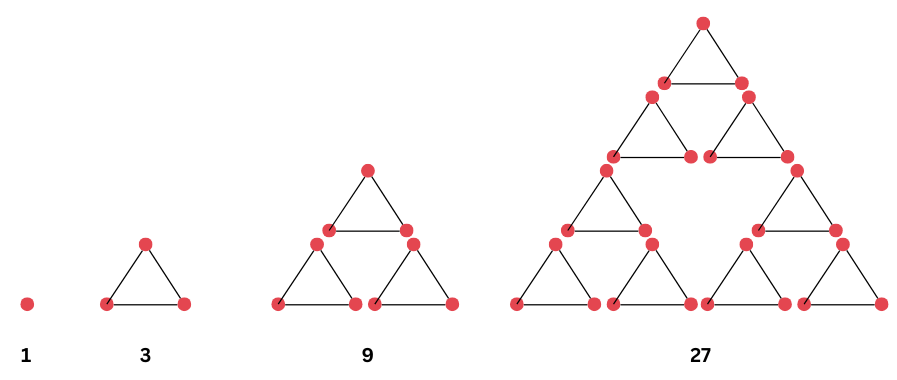
8. What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, …? Which sequence do you get? Can you explain it using a picture of a cube?
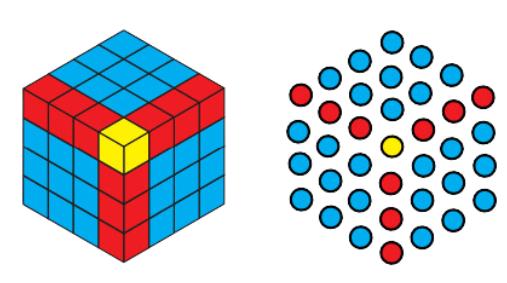
Answer:
1 = 1
1 + 7 = 8
1 + 7 + 19 = 27
1 + 7 + 19 + 37 = 64
The sequence is 1, 8, 27, 64, …. Which is the sequence of cubes.
Explanation using picture of cube:
- In the first step, you start out with a single cube.
- In the second step, you add a hexagon of 7 dots, which forms a larger cube comprising of 8 smaller cubes. This larger cube has dimensions 2 × 2 × 2.
- In the third step, you add a hexagon of 19 dots, which forms a larger cube comprising of 27 smaller cubes. This larger cube has dimensions of 3 × 3 × 3.
- We keep adding larger hexagons to form the Sequence of cubes.
9. Find your own patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?
Answer:
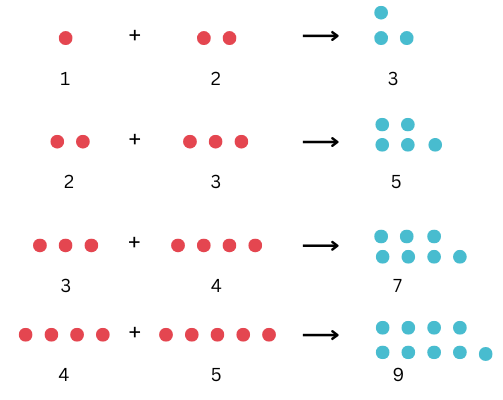
The Counting number sequence is as follows: 1, 2, 3, 4, 5, ….
We can see by adding consecutive counting numbers that:
1 + 2 = 3
2 + 3 = 5
3 + 4 = 7
4 + 5 = 9
Now adding 1 to the beginning to the beginning of the series we get the Odd number sequence as follows: 1, 3, 5, 7, 9, …
This can be explained with the help of a picture as follows:
Section 1.5
Figure it Out (Page 11):
1. Can you recognise the pattern in each of the sequences in Table 3?
Answer:
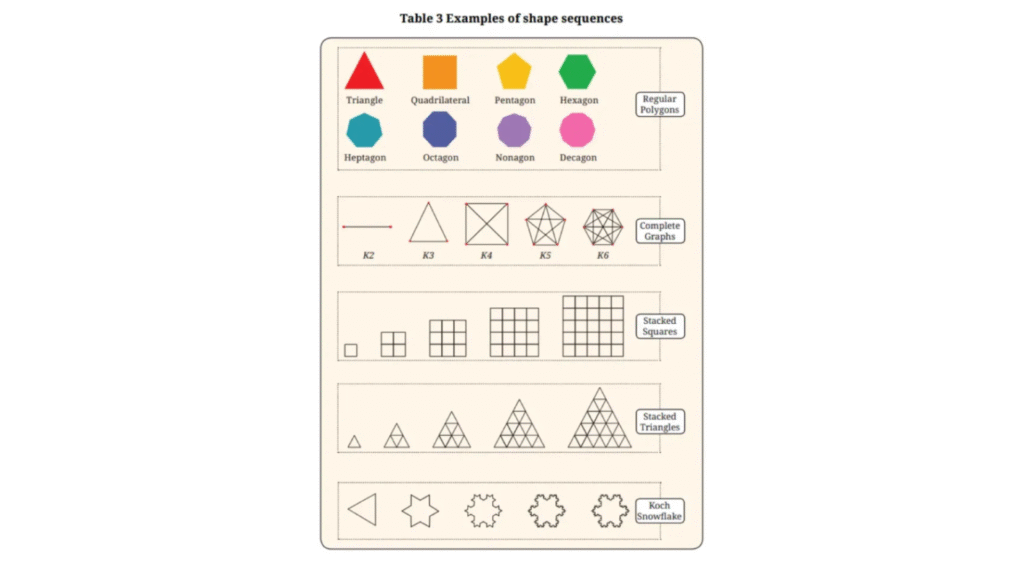
Regular Polygons: This sequence has polygons with increasing number of equal sides, starting from 3: (3, 4, 5, 6, 7, 8, 9, 10, …). Since they have equal sides they are called regular polygons.
Complete Graphs: This sequence can be written as Kn, where n represents the number of vertices. All vertices of each shape are joined together.
Stacked Squares: The number of stacked squares in the shapes is according to Squares series (1, 4, 9, 16, 25, ….).
Stacked Triangles: The number of stackedtriangles in the shapes is according to Squares series (1, 4, 9, 16, 25, ….).
Koch Snowflake: Each line segment in each shape bends to form one triangle as the sequence progresses.
2. Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Answer:

Rule: The number of sides increases by 1, starting from 3.

Rule: The number of vertices increases by 1, starting from 2.
Rule: Each side of the stacked squares increases by one small square.
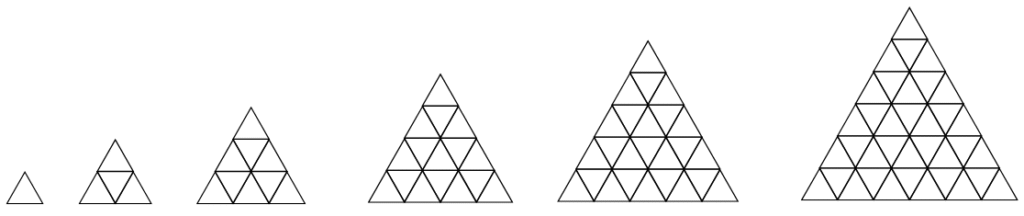
Rule: In each shape in the sequence, the number of triangles follow a Triangular series pattern.

Rule: Each sideof each shapebends to form two more sides as shown below:

The next shape in the Koch Snowflake sequence cannot be drawn due to the minute size of the lines which will make it impossible to see with the naked eye.
Figure it Out (Page 11):
1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Answer:
Counting the number of sides in each shape in the sequence of Regular Polygons, we get the following number sequence: 3, 4, 5, 6, 7, 8, 9, 10, ….
This is the Counting Numbers sequence starting from 3.
Counting the number of corners in each shape in the sequence of Regular Polygons, we get the following number sequence: 3, 4, 5, 6, 7, 8, 9, 10, …. This is also the Counting Numbers sequence starting from 3.
Therefore, we get the same number sequence because the number of sides = number of corners in a regular polygon.
2. Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?
Answer:
Counting the number of lines in each shape in the sequence of Complete Graphs, we get the following sequence: 1, 3, 6, 10, 15, …which is the Triangular number sequence.
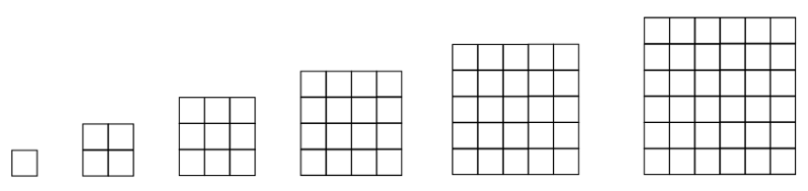
3. How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Answer:
Number of squares in each shape:
First shape = 1
Second shape = 4
Third shape = 9
Fourth shape = 16
Fifth shape = 25
This gives us the Squares number sequence: 1, 4, 9, 16, 25, … The reason is that the smaller squares have been stacked to form larger perfect squares.
4. How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why? (Hint: In each shape in the sequence, how many triangles are there in each row?)
Answer:
The number of little triangles that are there in each shape of the Stacked Triangles sequence:
First shape = 1
Second shape = 4
Third shape = 9
Fourth shape = 16
Fifth shape = 25
Therefore, we have the Triangular number sequence: 1, 4, 9, 16, 25, …
Adding the number of triangles in each row, we get:
First shape = 1
Second shape = 1 + 3 = 4
Third shape = 1 + 3 + 5 = 9
Fourth shape = 1 + 3 + 5 + 7 = 16
This gives us Triangular number sequence.
5. To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’ by a ‘speed bump’ . As one does this more and more times, the changes become tinier and tinier with very very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, …, i.e. 3 times Powers of 4; this sequence is not shown in Table 1)
Answer:
The number of line segments in each shape after counting:
First shape = 3
Second shape = 12 = 3 × 41
Third shape = 3 × 42
Fourth shape = 3 × 44
Therefore, the sequence is 3 times Powers of 4.


