Figure it Out (Page 108):
1. At what number is ‘idli-vada’ said for the 10th time?
Answer:
The first number for which the players said ‘idli-vada’ for the 1st time is 15, which is a multiple of 3, and also a multiple of 5.
We see that:
15 × 1 = 15,
15 × 2 = 30,
15 × 3 = 45,
And so on….
Continuing on in the same way, we see:
15 × 10 = 150
Therefore, ‘idli-vada’ is said for the 10th time at the number 150.
2. If the game is played for the numbers from 1 till 90, find out:
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
c. How many times would the children say ‘idli-vada’?
Answer:
a. The children say ‘idli’ when the number is a multiple of 3.
The multiples of 3 between 1 and 90 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90.
Total number of multiples of 3 from 1 to 90 = 30.
Therefore, the children said ‘idli’ 30 times.
b. The children say ‘vada’ when the number is a multiple of 5.
The multiples of 5 between 1 and 90 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90.
Total number of multiples of 5 from 1 to 90 = 18.
Therefore, the children said ‘vada’ 18 times.
c. The children say ‘idli-vada’ when the number is a multiple of both 3 and 5.
The multiples of 3 and 5 between 1 and 90 are: 15, 30, 45, 60, 75, 90.
Therefore, the children said ‘idli-vada’ 6 times.
3. What if the game was played till 900? How would your answers change?
Answer:
Total number of multiples of 3 from 1 to 90 = 30.
We observe that, 900 = 90 × 10.
Therefore, number of multiples of 3 from 1 to 900 = 30 × 10 = 300.
Therefore, the children said ‘idli’ 300 times.
Total number of multiples of 5 from 1 to 90 = 18.
Similarly, number of multiples of 5 from 1 to 900 = 18 × 10 = 180.
Therefore, the children said ‘vada’ 180 times.
Total number of multiples of 15 from 1 to 90 = 6.
Similarly, number of multiples of 15 from 1 to 900 = 6 × 10 = 60.
Therefore, the children said ‘idli-vada’ 60 times.
4. Is this figure somehow related to the ‘idli-vada’ game?
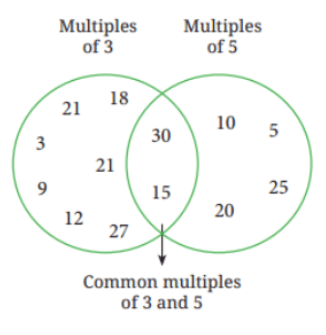
Hint: Imagine playing the game till 30. Draw the figure if the game is played till 60.
Answer:
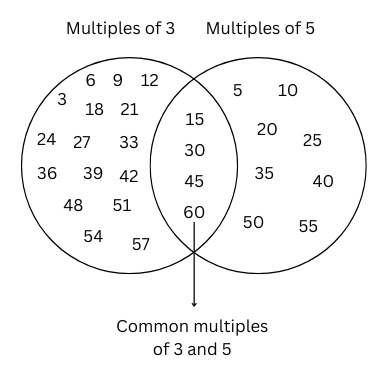
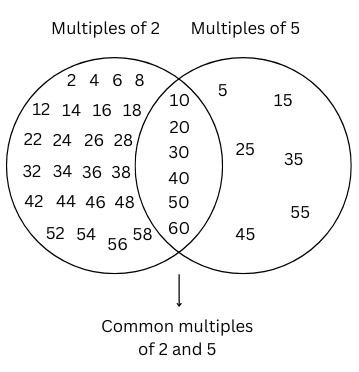
In-text Questions (Page 108):
Let us now play the ‘idli-vada’ game with different pairs of numbers:
a. 2 and 5,
b. 3 and 7,
c. 4 and 6.
We will say ‘idli’ for multiples of the smaller number, ‘vada’ for multiples of the larger number and ‘idli-vada’ for common multiples. Draw a figure similar to Fig. 5.1 if the game is played up to 60.
Answer:
a. 2 and 5
b. 3 and 7

c. 4 and 6
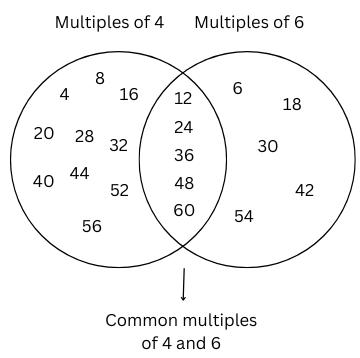
In-text Questions (Page 109):
Which of the following could be the other number:
2, 3, 5, 8, 10?
Answer:
The first number = 4.
The other number must be 8 because every multiple of 8 is also a multiple of 4. Hence, the second number = 8.
In-text Questions (Page 110):
What jump size can reach both 15 and 30? There are multiple jump sizes possible. Try to find them all.
Answer:
Factors of 15 = 1, 3, 5, 15.
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30.
Common factors of 15 and 30 are 1, 3, 5, 15.
Therefore, the jump size which can reach both 15 and 30 are 1, 3, 5, 15.
Look at the table below. What do you notice?

In the table,
1. Is there anything common among the shaded numbers?
2. Is there anything common among the circled numbers?
3. Which numbers are both shaded and circled? What are these numbers called?
Answer:
1. The shaded numbers are multiples of 3.
2. The circled numbers are multiples of 4.
3. The numbers which are both shaded and circled are multiples of both 3 and 4.
Figure it Out (Page 110):
1. Find all multiples of 40 that lie between 310 and 410.
Answer:
All multiples of 40 that lie between 310 and 410 can be done as follows:
40 × 8 = 320, 40 × 9 = 360, 40 × 10 = 400.
Therefore, all multiples of 40 that lie between 310 and 410 are 320, 360 and 400.
2. Who am I?
a. I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
b. I am a number less than 100. Two of my factors are 3 and 5. One of my digits is 1 more than the other.
Answer:
a. Let us take all numbers which are less than 40 with one factor as 7.
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
We see that the sum of the digits of 35 = 3 + 5 = 8.
Therefore, the required number is 35.
b. Two of the factors of the number are 3 and 5.
All such numbers less than 100 are as follows:
1 × (3 × 5) = 15
2 × (3 × 5) = 30
3 × (3 × 5) = 45
4 × (3 × 5) = 60
5 × (3 × 5) = 75
6 × (3 × 5) = 90
The only number in which one of the digits is 1 more than the other is 45.
Therefore, the required number is 45.
3. A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14 and 28. Their sum is 56 which is twice 28. Find a perfect number between 1 and 10.
Answer:
Factors of 6 = 1, 2, 3, 6.
Sum of the factors of 6 = 1 + 2 + 3 + 6 = 12.
12 is two times the number 6.
Therefore, a perfect number between 1 and 10 is 6.
4. Find the common factors of:
a. 20 and 28 b. 35 and 50
c. 4, 8 and 12 d. 5, 15 and 25
Answer:
a. 20 and 28
The factors of 20 = 1, 2, 4, 5, 10, 20.
The factors of 28 = 1, 2, 4, 7, 14, 28.
Therefore, the common factors of 20 and 28 = 1, 2, 4.
b. 35 and 50
The factors of 35 = 1, 5, 7.
The factors of 50 = 1, 2, 5, 10, 25, 50.
The common factors of 35 and 50 = 1, 5.
c. 4, 8 and 12
The factors of 4 = 1, 2, 4.
The factors of 8 = 1, 2, 4, 8.
The factors of 12 = 1, 2, 3, 4, 6, 12.
The common factors of 4, 8 and 12 = 1, 2, 4.
d. 5, 15 and 25
The factors of 5 = 1, 5.
The factors of 15 = 1, 3, 5, 15.
The factors of 25 = 1, 5, 25.
The common factors of 5, 15 and 25 = 1, 5.
5. Find any three numbers that are multiples of 25 but not multiples of 50.
Answer:
The multiples of 25 are: 25, 50, 75, 100, 125, 150, 175, 200.
The multiples of 50 are: 50, 100, 150, 200.
Comparing, we get the three numbers that are multiples of 25 but not multiples of 50 are: 25, 75, 125, 175.
6. Anshu and his friends play the ‘idli-vada’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idlivada’ is after the number 50. What could the two numbers be which are assigned ‘idli’ and ‘vada’?
Answer:
For pair (7, 8):
Multiples of 7 = 7, 14, 21, 28, 35, 42, 49, 56.
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56.
The first common multiple of 7 and 8 = 56 and is the first time anybody says ‘idlivada’. Therefore, one pair of numbers is (7, 8).
For pair (7, 9):
Multiples of 7 = 7, 14, 21, 28, 35, 42, 49, 56, 63.
Multiples of 9 = 9, 18, 27, 36, 45, 54, 63.
The first common multiple of 7 and 9 = 63 and is the first time anybody says ‘idlivada’. Therefore, one pair of numbers is (7, 9).
For pair (8, 9):
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72.
Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72.
The first common multiple of 8 and 9 = 72 and is the first time anybody says ‘idlivada’. Therefore, one pair of numbers is (8, 9).
7. In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Answer:
In the treasure hunting game, Grumpy has kept treasures on 28 and 70.
Therefore, the jump sizes that will land on both the numbers will be common factors of both 28 and 70.
Factors of 28 = 1, 2, 4, 7, 14, 28.
Factors of 70 = 1, 2, 5, 7, 10, 14, 35, 70.
Common factors of 28 and 70 = 1, 2, 7, 14.
8. In the diagram below, Guna has erased all the numbers except the common multiples. Find out what those numbers could be and fill in the missing numbers in the empty regions.
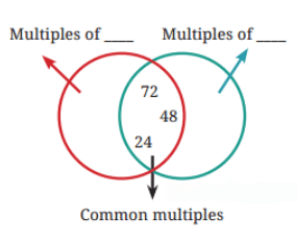
Answer:
(6, 8) is one pair of numbers whose common multiples are 24, 48, 72. The empty regions for the pair (6,8) filled out is shown below:
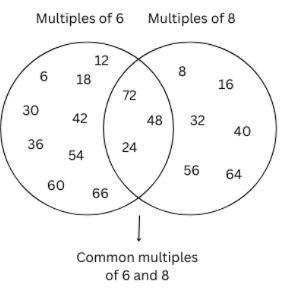
(3, 8) is another pair of numbers whose common multiples are 24, 48, 72. The empty regions for the pair (3, 8) filled out is shown below:
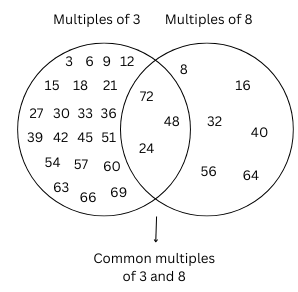
(8, 12) is another pair of numbers whose common multiples are 24, 48, 72. The empty regions for the pair (8, 12) filled out is shown below:

9. Find the smallest number that is a multiple of all the numbers from 1 to 10 except for 7.
Answer:
The smallest number that is a multiple of all the numbers from 1 to 10 except for 7 will be the LCM of 1, 2, 3, 4, 5, 6, 8, 9, 10. The LCM can be found as below:

LCM = 2 × 2 × 3 × 5 × 2 × 3 = 360.
Therefore, the smallest number that is a multiple of all the numbers from 1 to 10 except for 7 is 360.
10. Find the smallest number that is a multiple of all the numbers from 1 to 10.
Answer:
The smallestnumber that is a multiple of all the numbers from 1 to 10 will be the LCM of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The LCM can be found as below:

LCM = 2 × 2 × 3 × 5 × 7 × 2 × 3 = 2520.
Therefore, the smallest number that is a multiple of all the numbers from 1 to 10 is 2520.
In-Text Questions (Page 113):
How many prime numbers are there from 21 to 30? How many composite numbers are there from 21 to 30?
Answer:
There are 2 prime numbers from 21 to 30: 23 and 29.
There are 8 composite numbers from 21 to 30: 21, 22, 24, 25, 26, 27, 28, 30.
Figure it Out (Page 114-115):
1. We see that 2 is a prime and also an even number. Is there any other even prime?
Answer:
No, there are no other even primes other than 2.
Reason: All even numbers other than 2 are divisible by numbers other than 1 and the number itself.
2. Look at the list of primes till 100. What is the smallest difference between two successive primes? What is the largest difference?
Answer:
Looking at the list of primes till 100, we can see that:
The smallest difference between two successive primes = 3 – 2 = 1.
The largest difference between two successive primes = 97 – 89 = 8.
3. Are there an equal number of primes occurring in every row in the table on the previous page? Which decades have the least number of primes? Which have the most number of primes?
Answer:
No, every row in the table on the previous page do not have an equal number of primes.
The decade 91-100 has the least number of primes with only 1 prime number which is 97.
The decades 1 – 10, 11 – 20 have the most number of primes (4 each).
4. Which of the following numbers are prime? 23, 51, 37, 26
Answer:
The numbers 23 and 37 are prime numbers as 1 and the number itself are the only factors in both cases.
5. Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Answer:
The pairs of prime numbers less than 20 whose sum is a multiple of 5 are as follows:
(2, 3) = 2 + 3 = 5
(3, 7) = 3 + 7 = 10
(2, 13) = 2 + 13 = 15
(7, 13) = 7 + 13 = 20
(3, 17) = 3 + 17 = 20
6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Answer:
Pairs of prime numbers up to 100 having the same digits are 17 and 71, 37 and 73, 79 and 97.
7. Find seven consecutive composite numbers between 1 and 100.
Answer:
Seven consecutive composite numbers between 1 and 100 are 90, 91, 92, 93, 94, 95, 96.
8. Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between 1 and 100.
Answer:
Twin primes between 1 and 100 are: (5, 7), (11, 13), (29, 31), (41, 43), (59, 61), (71, 73).
9. Identify whether each statement is true or false. Explain.
a. There is no prime number whose units digit is 4.
b. A product of primes can also be prime.
c. Prime numbers do not have any factors.
d. All even numbers are composite numbers.
e. 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Answer:
a. True.
Explanation: A prime number whose units digit is 4 cannot be a prime number because it will always be divisible by at least 2, being an even number.
b. False.
Explanation: A product of primes cannot be prime because a prime number has exactly two distinct factors: 1 and itself (e.g., 2, 3, 5, 7). A product of two or more primes always has more than two factors, making it composite, not prime.
c. False.
Explanation: A prime number has exactly two distinct factors: 1 and itself.
d. False.
Explanation: The smallest even number 2 is a prime number.
e. True.
Explanation: Except 2, all other prime numbers are odd. Therefore, if you add 1 to them, you get an even number which is composite.
10. Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Answer:
The numbers 45, 60, 91, 105, 330 divided into prime factors are shown below:
45 = 3 × 3 × 5
60 = 2 × 2 × 3 × 5
91 = 7 × 13
105 = 3 × 5 × 7
330 = 2 × 3 × 5 × 7
Therefore, 105 is the product of exactly three distinct prime numbers 3, 5 and 7.
11. How many three-digit prime numbers can you make using each of 2, 4 and 5 once?
Answer:
We can make 0 three-digit numbers using each of 2, 4 and 5 once.
The numbers can end with 2, 4 or 5.
If the numbers end with 2 or 4, they will always be divisible by 2.
If the numbers end with 5, they will always be divisible by 5.
Hence, we can make 0 three-digit numbers using each of 2, 4 and 5 once.
12. Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Answer:
Yes, the other primes for which doubling and adding 1 gives another prime are as follows:
2 × 2 + 1 = 5 (Prime)
5 × 2 + 1 = 11 (Prime)
11 × 2 + 1 = 23 (Prime)
23 × 2 + 1 = 47 (Prime)
29 × 2 + 1 = 59 (Prime)
Therefore, 2, 5, 11, 23 and 29 are five such examples.
In-text Questions (Page 115):
Where should Grumpy place the treasures so that Jumpy cannot reach both the treasures?
Check if these pairs are safe:
a. 15 and 39 b. 4 and 15
c. 18 and 29 d. 20 and 55
Answer: (b) and (c) are safe.
Explanation:
a. 15 and 39
15 = 3 × 5
39 = 3 × 13
3 is a common factor and so the above pair is not co-prime. Hence, the above pair is not safe because if the jump size is chosen to be 3, then Jumpy will reach both 15 and 39.
b. 4 and 15
4 = 2 × 2
15 = 3 × 5
Therefore, 4 and 15 are co-prime numbers and hence is a safe pair.
c. 18 and 29
18 = 2 × 3 × 3
29 = 1 × 29
Therefore, 18 and 29 are co-prime and hence is a safe pair.
d. 20 and 55
20 = 2 × 2 × 5
55 = 5 × 11
5 is a common factor and so the above pair is not co-prime. Hence, the above pair is not safe because if the jump size is chosen to be 5, then Jumpy will reach both 20 and 55.
In-text Questions (Page 116):
Which of the following pairs of numbers are co-prime?
a. 18 and 35 b. 15 and 37 c. 30 and 415
d. 17 and 69 e. 81 and 18
Answer:
a. 18 and 35
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 35 = 1, 5, 7, 35
Since, 18 and 35 have no common factors, they are co-prime.
b. 15 and 37
Factors of 15 = 1, 3, 5, 15
Factors of 37 = 1, 37
Since, 15 and 37 have no common factors, they are co-prime.
c. 30 and 415
Factors of 30 = 1, 2, 3, 5, 6, 15, 30
Factors of 415 = 1, 5, 83, 415.
Common factor = 5.
Since, 30 and 415 have 5 as a common factor, they are not co-prime.
d. 17 and 69
Factors of 17 = 1, 17
Factors of 69 = 1, 3, 23, 69
Since, 17 and 69 have no common factors, they are co-prime.
e. 81 and 18
Factors of 81 = 3, 9, 27, 81
Factors of 18 = 1, 2, 3, 6, 9, 18
Common factors = 3, 9
Since, 81 and 18 have 3 and 9 as common factors, they are co-prime.
In-text Questions (Page 116):
Observe the following thread art. The first diagram has 12 pegs and the thread is tied to every fourth peg (we say that the thread-gap is 4). The second diagram has 13 pegs and the thread-gap is 3. What about the other diagrams? Observe these pictures, share and discuss your findings in class.
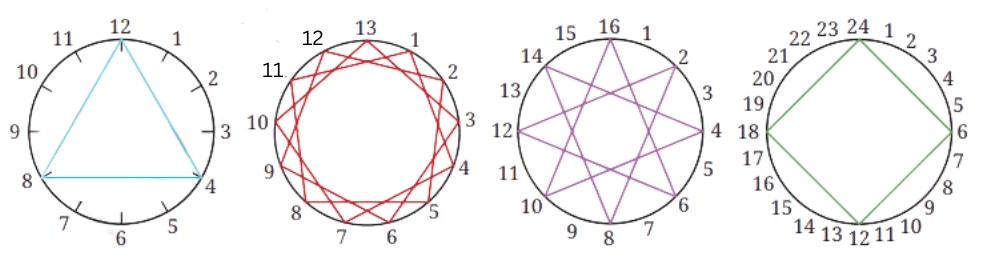
In some diagrams, the thread is tied to every peg. In some, it is not. Is it related to the two numbers (the number of pegs and the thread-gap) being co-prime?
Make such pictures for the following:
a. 15 pegs, thread-gap of 10 b. 10 pegs, thread-gap of 7
c. 14 pegs, thread-gap of 6 d. 8 pegs, thread-gap of 3
Answer:
Answer:
Third Diagram: 16 pegs, thread gap of 6
Fourth Diagram: 24 pegs, thread gap of 6
The thread is tied to every peg if the two numbers (the number of pegs and the thread-gap) are co-prime. This is seen only in the third diagram where the number of pegs (13) and thread-gap (3) are co-prime.
a. 15 pegs, thread-gap of 10

b. 10 pegs, thread-gap of 7
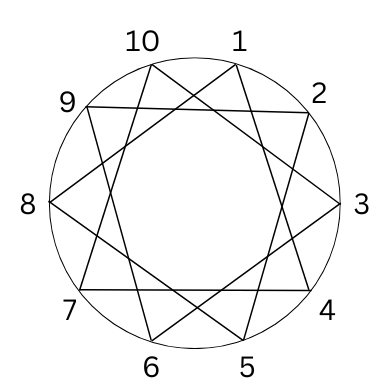
c. 14 pegs, thread-gap of 6
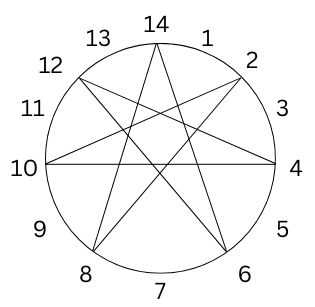
d. 8 pegs, thread-gap of 3
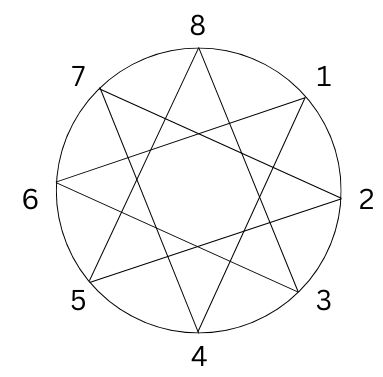
In-text Questions (Page 117):
But where did Anshu go wrong?
Answer:
Anshu was wrong was incomplete factorisation. He did not break up the numbers 56 and 63 into its prime factors to check whether any common factors exist. Hence, he arrived at the wrong conclusion.
Figure it Out (Page 120):
1. Find the prime factorisations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Answer:
64 = 2 × 2 × 2 × 2 × 2 × 2
104 = 2 × 2 × 3 × 13
105 = 3 × 5 × 7
243 = 3 × 3 × 3 × 3 × 3
320 = 2 × 2 × 2 × 2 × 2 × 2 × 5
141 = 3 × 47
1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
729 = 3 × 3 × 3 × 3 × 3 × 3
1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
1331 = 11 × 11 × 11
1000 = 2 × 2 × 2 × 5 × 5 × 5
2. The prime factorisation of a number has one 2, two 3s, and one 11. What is the number?
Answer:
The number will be the product of its prime factors.
Therefore,
Number = 2 × 3 × 3 × 11 = 198
3. Find three prime numbers, all less than 30, whose product is 1955.
Answer:
Prime factorisation of 1955 = 5 × 17 × 23
Therefore, the three prime numbers are 5, 17 and 23.
4. Find the prime factorisation of these numbers without multiplying first
a. 56 × 25 b. 108 × 75 c. 1000 × 81
Answer:
a. 56 × 25
Prime factorisation is shown below:
56 = 2 × 2 × 2 × 7 and
25 = 5 × 5
Therefore,
56 × 25 = 2 × 2 × 2 × 5 × 5 × 7
b. 108 × 75
Prime factorisation is shown below:
108 = 2 × 2 × 3 × 3 × 3 and
75 = 3 × 5 × 5
Therefore,
108 × 75 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
c. 1000 × 81
Prime factorisation is shown below:
1000 = 2 × 2 × 2 × 5 × 5 × 5
81 = 3 × 3 × 3 × 3
Therefore,
1000 × 81 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 5
5. What is the smallest number whose prime factorisation has:
a. three different prime numbers?
b. four different prime numbers?
Answer:
a. To find the smallest number whose prime factorisation hasthree different prime numbers, we need the three smallest prime numbers: 2, 3, 5.
Prime factorisation = 2 × 3 × 5 = 30.
b. To find the smallest number whose prime factorisation hasfour different prime numbers, we need the four smallest prime numbers: 2, 3, 5, 7.
Prime factorisation = 2 × 3 × 5 × 7 = 210.
Figure it Out (Page 122):
1. Are the following pairs of numbers co-prime? Guess first and then use prime factorisation to verify your answer.
a. 30 and 45 b. 57 and 85
c. 121 and 1331 d. 343 and 216
Answer:
a. 30 and 45
My guess is that the numbers are not co-prime.
Prime factorisation:
30 = 2 × 3 × 5
45 = 3 × 3 × 5
Common factors = 3, 5.
Therefore, these numbers are not co-prime. My guess was correct.
b. 57 and 85
My guess is that the numbers are co-prime.
Prime factorisation:
57 = 3 × 19
85 = 5 × 17
There are no common factors.
Therefore, these numbers are co-prime. My guess was correct.
c. 121 and 1331
My guess is that the numbers are co-prime.
Prime factorisation:
121 = 11 × 11
1331 = 11 × 11 × 11
Common factor = 11
Therefore, these numbers are not co-prime. My guess was incorrect.
d. 343 and 216
My guess is that the numbers are co-prime.
Prime factorisation:
343 = 7 × 7 × 7
216 = 2 × 2 × 2 × 3 × 3 × 3
There are no common factors.
Therefore, these numbers are co-prime. My guess was correct.
2. Is the first number divisible by the second? Use prime factorisation.
a. 225 and 27 b. 96 and 24
c. 343 and 17 d. 999 and 99
Answer:
a. 225 and 27
We can say that if one number is divisible by another, then the prime factorisation of the second number is included in the prime factorisation of the first number.
Prime Factorisation:
225 = 3 × 3 × 5 × 5
27 = 3 × 3 × 3
225 has two 3’s and 27 has three 3’s as factors.
Therefore, the entire prime factorisation of 27 is not included in 225 and we conclude that 225 is not divisible by 27.
b. 96 and 24
We can say that if one number is divisible by another, then the prime factorisation of the second number is included in the prime factorisation of the first number.
Prime Factorisation:
96 = 2 × 2 × 2 × 2 × 2 × 3
24 = 2 × 2 × 2 × 3
The entire prime factorisation of 24 is included in 96 and hence we conclude that 96 is divisible by 24.
c. 343 and 17
We can say that if one number is divisible by another, then the prime factorisation of the second number is included in the prime factorisation of the first number.
Prime Factorisation:
343 = 7 × 7 × 7
17 = 1 × 17
Therefore, the entire prime factorisation of 17 is not included in 343 and we conclude that 343 is not divisible by 17.
d. 999 and 99
We can say that if one number is divisible by another, then the prime factorisation of the second number is included in the prime factorisation of the first number.
Prime Factorisation:
999 = 3 × 3 × 3 × 37
99 = 3 × 3 × 11
Therefore, the entire prime factorisation of 99 is not included in 999 and we conclude that 999 is not divisible by 99.
3. The first number has prime factorisation 2 × 3 × 7 and the second number has prime factorisation 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Answer:
Prime factorisation:
First Number = 2 × 3 × 7
Second Number = 3 × 7 × 11
The two numbers have two common factors: 3 and 7. Therefore, they are not co-prime.
Neither number divides the other because the prime factors of each are different.
4. Guna says, “Any two prime numbers are co-prime”. Is he right?
Answer:
The statement that any two prime numbers are co-prime is right. This is because the only common factor that prime numbers have is 1.
In-text Questions (Page 123):
Consider this statement: Numbers that are divisible by 10 are those that end with ‘0’. Do you agree?
Answer:
I agree with the statement that numbers that are divisible by 10 are those that end with ‘0’. For example, 20, 400, 1500 and 10,000 all end with 0 and are divisible by 10.
In-text Questions (Page 123):
Consider this statement: Numbers that are divisible by 5 are those that end with either a ‘0’ or a ‘5’. Do you agree?
Answer:
I agree with the statement that numbers that are divisible by 5 are those that end with either a ‘0’ or a ‘5’.
If 5 is multiplied by an even number the product ends in 0 and if 5 is multiplied by an odd number the product ends in 5.
We observe that 15, 20, 75, 100, 1225, 15000, 15005 are all divisible by 5.
In-text Questions (Page 124):
Consider this statement:
Numbers that are divisible by 2 are those that end with ‘0’, ‘2’, ‘4, ‘6’ or ‘8’. Do you agree?
What are all the multiples of 2 between 399 and 411?
Answer:
I agree with the statement that numbers that are divisible by 2 are those that end with ‘0’, ‘2’, ‘4, ‘6’ or ‘8’. The reason is that for a number to be divisible by 2, it must be an even number. All even numbers end with the digits ‘0’, ‘2’, ‘4, ‘6’ or ‘8’.
The multiples of 2 between 399 and 411 are 400, 402, 404, 406, 408, 410.
In-text Questions (Page 124):
Find numbers between 330 and 340 that are divisible by 4. Also, find numbers between 1730 and 1740, and 2030 and 2040, that are divisible by 4. What do you observe?
Answer:
Numbers divisible by 4 between 330 and 340: 332, 336, 340
Numbers divisible by 4 between 1730 and 1740: 1732, 1736, 1740
Numbers divisible by 4 between 2030 and 2040: 2032, 2036, 2040
We observe that last two-digits of the numbers (32, 36 and 40) are divisible by 4. Therefore, we conclude that if the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
In-text Questions (Page 124):
Is 8536 divisible by 4?
Answer:
We observe that last two-digits of the number 8636 i.e. 36 are divisible by 4. Therefore, the number 8536 is divisible by 4.
In-text Questions (Page 124):
Consider these statements:
a. Only the last two digits matter when deciding if a given number is divisible by 4.
b. If the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
c. If the original number is divisible by 4, then the number formed by the last two digits is divisible by 4.
Do you agree? Why or why not?
Answer:
a. True.
Reason: It has been observed that if the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
b. True.
Reason: It has been observed that if the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
c. True.
Reason: It has been observed that if the number formed by the last two digits is divisible by 4, then the original number is divisible by 4. Therefore, the converse is also true.
In-text Questions (Page 125):
Find numbers between 120 and 140 that are divisible by 8. Also find numbers between 1120 and 1140, and 3120 and 3140, that are divisible by 8. What do you observe?
Answer:
It has been observed that if the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
The numbers between 120 and 140 divisible by 8are 120, 128 and 136.
The numbers between 1120 and 1140 divisible by 8are 1120, 1128 and 1136.
The numbers between 3120 and 3140 divisible by 8are 3120, 3128 and 3136.
Observation: If the number formed by the last three digits is divisible by 8, then the original number is divisible by 8.
In-text Questions (Page 125):
Change the last two digits of 8560 so that the resulting number is a multiple of 8.
Answer:
We change the last two digits of 8560 to get the following numbers: 8528, 8544, 8576. These numbers are all multiples of 8 because the last three digits are multiples of 8.
In-text Questions (Page 125):
Consider this statement:
a. Only the last three digits matter when deciding if a given number is divisible by 8.
b. If the number formed by the last three digits is divisible by 8, then the original number is divisible by 8.
c. If the original number is divisible by 8, then the number formed by the last three digits is divisible by 8.
Do you agree? Why or why not?
Answer:
a. True.
Reason: If the number formed by the last three digits is divisible by 8, then the original number is divisible by 8.
b. True.
Reason: If only the number formed by the last three digits is divisible by 8, then the original number is divisible by 8.
c. True.
Reason: If the number formed by the last three digits is divisible by 8, then the original number is divisible by 8. Therefore, the converse is also true.
Figure it Out (Page 125):
1. 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, except for those years that are evenly divisible by 100 but not 400.
a. From the year you were born till now, which years were leap years?
b. From the year 2024 till 2099, how many leap years are there?
Answer:
a. I was born in the year 2011. Till now the leap years were 2012, 2016, 2020 and 2024.
b. From the year 2024 till 2099, the leap years were 2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, 2096.
Therefore, there were 19 leap years.
2. Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Answer:
Largest 4-digit numbers that are divisible by 4 and are palindromes = 8888.
Smallest 4-digit numbers that are divisible by 4 and are palindromes = 2112.
3. Explore and find out if each statement is always true, sometimes true or never true. You can give examples to support your reasoning.
a. Sum of two even numbers gives a multiple of 4.
b. Sum of two odd numbers gives a multiple of 4.
Answer:
a. Sum of two even numbers gives a multiple of 4.
Sometimes true.
Explanation: There are cases where sum of two even numbers give a multiple of 4:
4 + 8 = 12, which is a multiple of 4.
6 + 10 = 16, which is a multiple of 4.
There are cases where sum of two even numbers does not give a multiple of 4:
4 + 2 = 6, which is not a multiple of 4.
10 + 12 = 22, which is not a multiple of 4.
b. Sum of two odd numbers gives a multiple of 4.
Sometimes true.
Explanation: There are cases where sum of two odd numbers give a multiple of 4:
7 + 9 = 16, which is a multiple of 4.
3 + 17 = 20, which is a multiple of 4.
There are cases where sum of two odd numbers does not give a multiple of 4:
7 + 11 = 18, which is not a multiple of 4.
5 + 9 = 14, which is not a multiple of 4.
4. Find the remainders obtained when each of the following numbers are divided by i) 10, ii) 5, iii) 2.
78, 99, 173, 572, 980, 1111, 2345.
Answer:
78:
(i) 78 ÷ 10 leaves a remainder of 8.
(ii) 78 ÷ 5 leaves a remainder of 3.
(iii) 78 ÷ 2 leaves a remainder of 0.
99:
(i) 99 ÷ 10 leaves a remainder of 9.
(ii) 99 ÷ 5 leaves a remainder of 4.
(iii) 99 ÷ 2 leaves a remainder of 1.
173:
(i) 173 ÷ 10 leaves a remainder of 3.
(ii) 173 ÷ 5 leaves a remainder of 3.
(iii) 173 ÷ 2 leaves a remainder of 1.
572:
(i) 572 ÷ 10 leaves a remainder of 2.
(ii) 572 ÷ 5 leaves a remainder of 2.
(iii) 572 ÷ 2 leaves a remainder of 0.
980:
(i) 980 ÷ 10 leaves a remainder of 0.
(ii) 980 ÷ 5 leaves a remainder of 0.
(iii) 980 ÷ 2 leaves a remainder of 0.
1111:
(i) 1111 ÷ 10 leaves a remainder of 1.
(ii) 1111 ÷ 5 leaves a remainder of 1.
(iii) 1111 ÷ 2 leaves a remainder of 1.
2345:
(i) 2345 ÷ 10 leaves a remainder of 5.
(ii) 2345 ÷ 5 leaves a remainder of 0.
(iii) 2345 ÷ 2 leaves a remainder of 1.
5. The teacher asked if 14560 is divisible by all of 2, 4, 5, 8 and 10. Guna checked for divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Answer:
The required numbers are 8 and 10.
Explanation:
If 14560 is divisible by 8, then it will be divisible 2, 4 because 2,4 are factors of 8.
If 14560 is divisible by 10, then it will be divisible by 2, 5 because 2, 5 are factors of 10.
6. Which of the following numbers are divisible by all of 2, 4, 5, 8 and 10: 572, 2352, 5600, 6000, 77622160.
Answer:
| Divisibility by 2 | Divisibility by 4 | Divisibility by 5 | Divisibility by 8 | Divisibility by 10 | Divisibility by All | |
| 572 | Number ends with 2, hence it is divisible by 2. | The number formed by the last two digits, i.e. 72 is divisible by 4, hence number is divisible by 4. | Number does not end with 0 or 5, hence number is not divisible by 5. | Last 3-digits of number 572 is not divisible by 8, so number is not divisible by 8. | Last digit of the number ends with 2 and not with 0, hence number is not divisible by 10. | No |
| 2352 | Number ends with 2, hence it is divisible by 2. | The number formed by the last two digits, i.e. 52 is divisible by 4, hence number is divisible by 4. | Number does not end with 0 or 5, hence number is not divisible by 5. | Last 3-digits i.e. 352 of number is divisible by 8, so number is divisible by 8. | Last digit of the number ends with 2 and not with 0, hence number is not divisible by 10. | No |
| 5600 | Number ends with 0, hence it is divisible by 2. | The number formed by the last two digits, i.e. 00 is divisible by 4, hence number is divisible by 4. | Number ends with 0, hence number is divisible by 5. | Last 3-digits of number i.e. 600 is divisible by 8, so number is divisible by 8. | Last digit of the number ends with 0, hence number is divisible by 10. | Yes |
| 6000 | Number ends with 0, hence it is divisible by 2. | The number formed by the last two digits, i.e. 00 is divisible by 4, hence number is divisible by 4. | Number ends with 0, hence number is divisible by 5. | Last 3-digits of number i.e. 000 is divisible by 8, so number is divisible by 8. | Last digit of the number ends with 0, hence number is divisible by 10. | Yes |
| 77622160 | Number ends with 0, hence it is divisible by 2. | The number formed by the last two digits, i.e. 60 is divisible by 4, hence number is divisible by 4. | Number ends with 0, hence number is divisible by 5. | Last 3-digits of number i.e. 160 is divisible by 8, so number is divisible by 8. | Last digit of the number ends with 0, hence number is divisible by 10. | Yes |
Therefore, the numbers are divisible by all of 2, 4, 5, 8 and 10 are 5600, 6000, 77622160.
7. Write two numbers whose product is 10000. The two numbers should not have 0 as the units digit.
Answer:
Prime factorisation = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 = (2 × 2 × 2 × 2) × (5 × 5 × 5 × 5) = 16 × 625.
Therefore, two numbers whose product is 10000 and which have 0 as the units digit are 16 and 25.
In-text Questions (Page 127):
Below are some boxes with four numbers in each box. Within each box try to say how each number is special compared to the rest. Share with your classmates and find out who else gave the same reasons as you did. Did anyone give different reasons that may not have occurred to you?!

Answer:
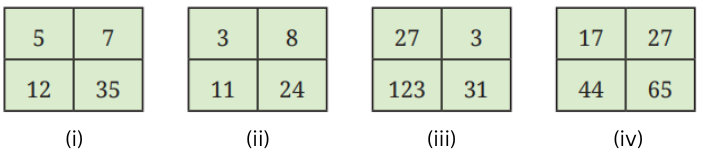
(i) 12 is special compared to the rest. The reason is that 5 and 7 are factors of 35, whereas 12 is not.
(ii) 11 is special compared to the rest. The reason is that 3 and 8 are factors of 24, whereas 11 is not.
(iii) 31 is special compared to the rest. The reason is that the other numbers are multiples of 3, whereas 31 is not.
(iv) 17 is special compared to the rest because 17 is a prime number.
In-text Questions (Page 127):
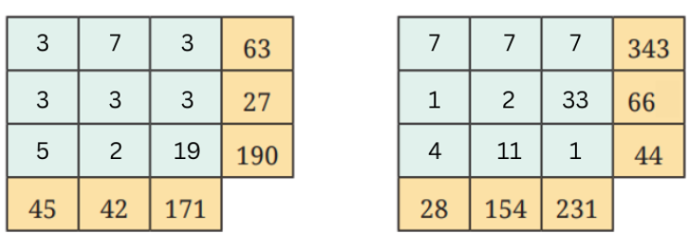
A Prime Puzzle
The figure on the left shows the puzzle. The figure on the right shows the solution of the puzzle. Think what the rules can be to solve the puzzle.
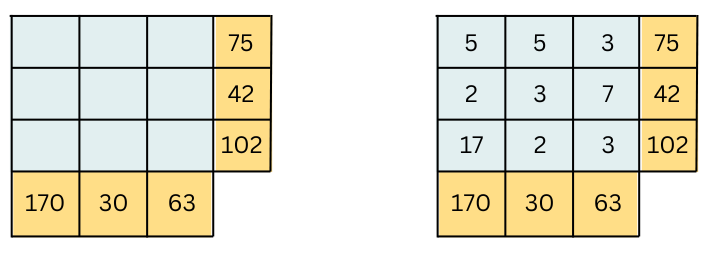
Answer:
Rule: The product of each row is the number to the right of the row and the product of each column is the number below the column.
Rules (Page 127)
Fill the grid with prime numbers only so that the product of each row is the number to the right of the row and the product of each column is the number below the column.
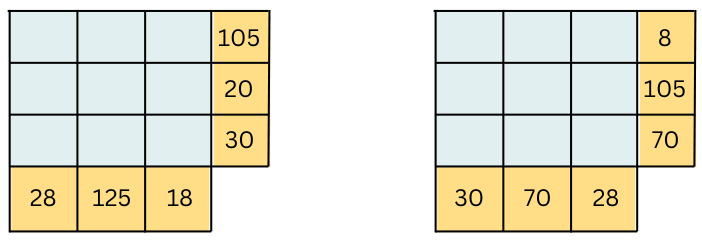
Answer:
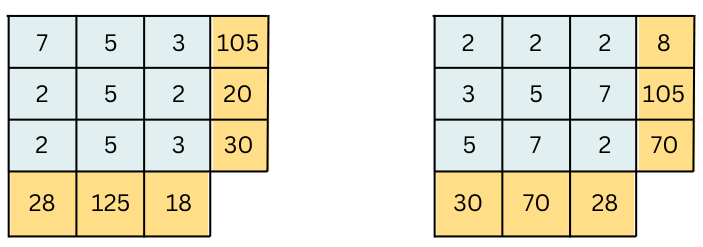
Page 128:
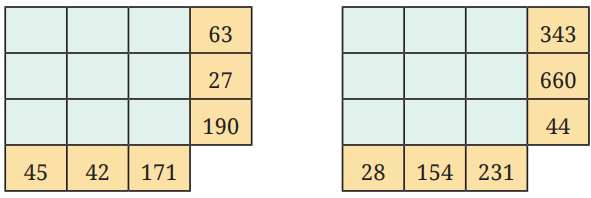
Answer: