Figure it Out (Page 15):
1.

Can you help Rihan and Sheetal find their answers?
Answer:
Rihan can draw countless or infinite number of lines that pass through the point.
Sheetal can draw only one line that passes through both of the points.
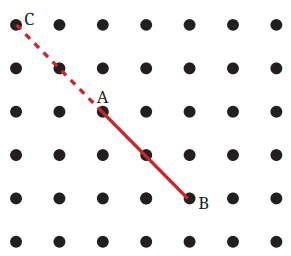
2. Name the line segments in Fig. 2.4. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?
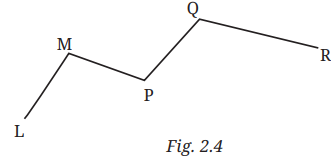
Answer:
The line segments in Fig. 2.4 are as follows: ,
,
,
.
Points L and R are on exactly one of the line segments. Points M, P, Q are on two of the line segments.
3. Name the rays shown in Fig. 2.5. Is T the starting point of each of these rays?
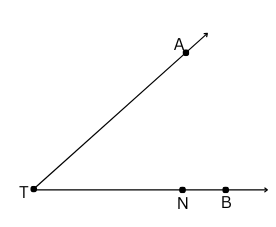
Answer:
The rays shown in Fig. 2.5 are: ,
,
,
. T is not the starting point of ray
.
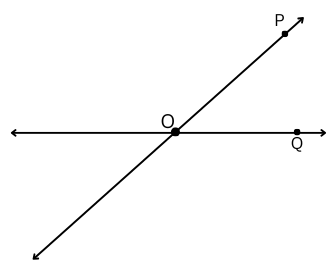
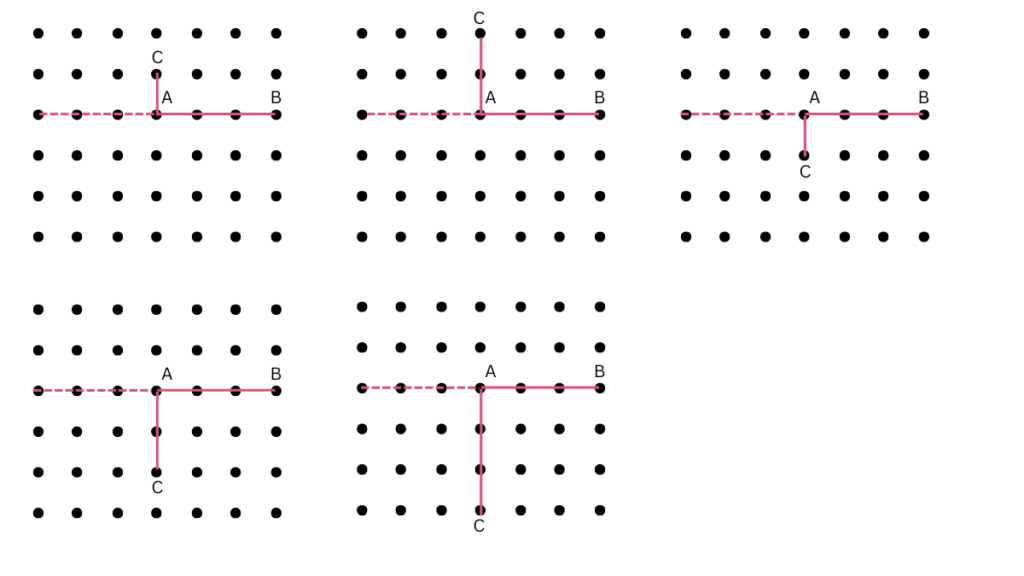
4. Draw a rough figure and write labels appropriately to illustrate each of the following:
a. and
meet at O.
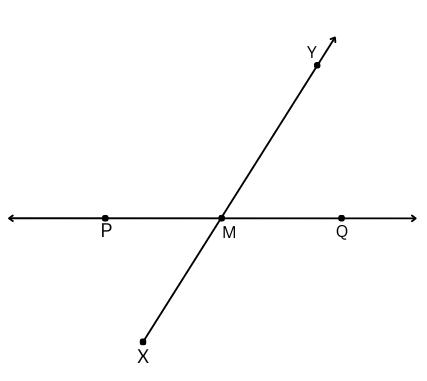
b. and
intersect at point M.
c. Line l contains points E and F but not point D.
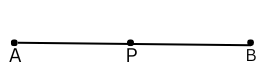
d. Point P lies on AB.
Answer:
a. The figure is shown below:
b. The figure is shown below:
c. The figure is shown below:
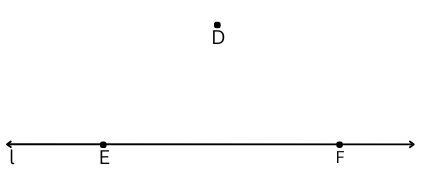
d. The figure is shown below:
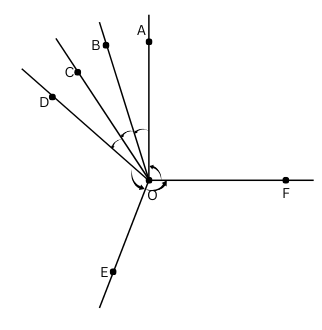
5. In Fig. 2.6, name:
a. Five points
b. A line
c. Four rays
d. Five line segments
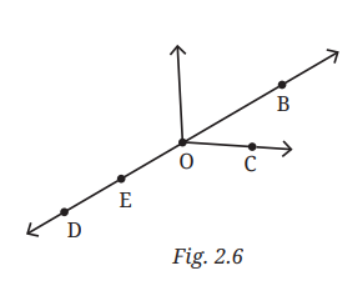
Answer:
a. Five points are O, B, C, E and D.
b. is the line.
c. ,
,
,
are four rays.
d. ,
,
,
,
ae five line segments.
6. Here is a ray (Fig. 2.7). It starts at O and passes through the point A. It also passes through the point B.
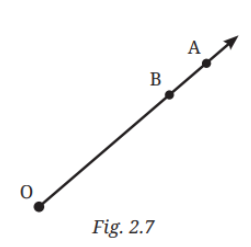
a. Can you also name it as ? Why?
b. Can we write as
? Why or why not?
Answer:
a. A ray starts from an initial point and passes through another point. Since the ray passes through point B as well, it can also be named as
.
b. cannot be written as
because they are opposite in direction.
starts from point O and passes through A and
starts from A and passes through O, hence they are opposite in direction.
Figure it Out (Page 19):
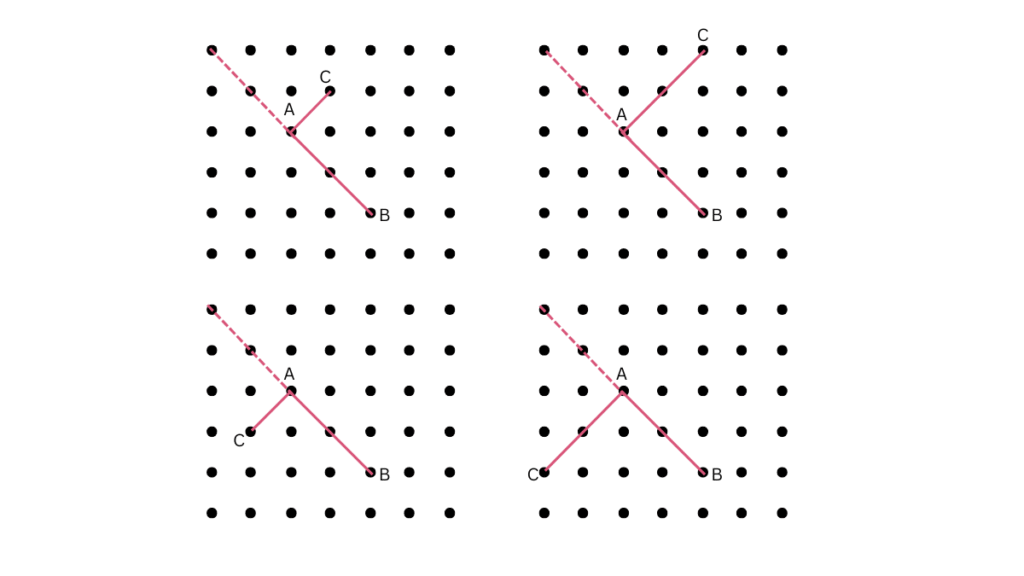
1. Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.

Answer:
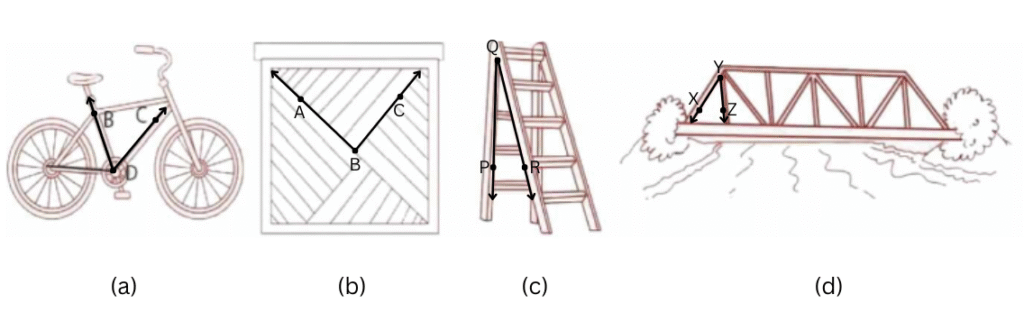
For Figure (a):
D is the vertex, and
are the rays.
For Figure (b):
B is the vertex, and
are the rays.
For Figure (c):
Q is the vertex, and
are the rays.
For Figure (d):
Y is the vertex, and
are the rays.
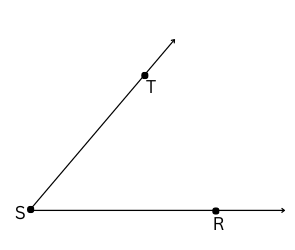
2. Draw and label an angle with arms ST and SR.
Answer:
In ∠ TSR shown below, S is the vertex and and
are the rays.
3. Explain why ∠APC cannot be labelled as ∠P.
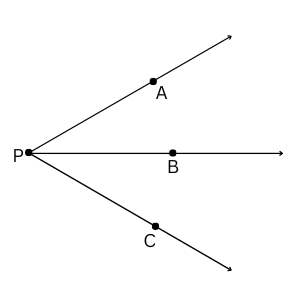
Answer:
∠APC cannot be labelled as ∠P because there are three angles, namely ∠APB, ∠BPC and ∠APC, with the same vertex P.
4. Name the angles marked in the given figure.
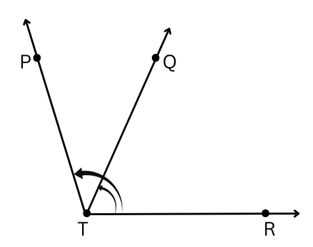
Answer:
The angles marked in the given figure are ∠RTQ and ∠RTP.
5. Mark any three points on your paper that are not on one line. Label them A, B, C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. 2.9.
Answer:
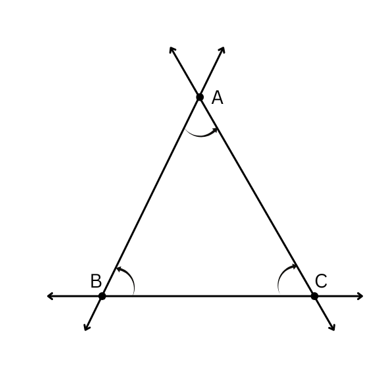
Three points A, B and C are drawn such that they are not on one line, as shown above.
Lines ,
and
are the three lines we can drawgoing through pairs of these points.
The angles that can be named using A, B and C are ∠ABC, ∠ACB and ∠BAC.
6. Now mark any four points on your paper so that no three of them are on one line. Label them A, B, C, D. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C, D? Write them all down, and mark each of them with a curve as in Fig. 2.9.
Answer:
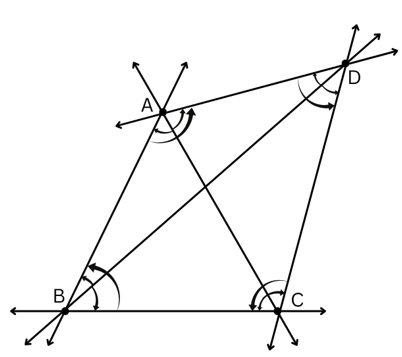
A, B, C and D are four points so that no three of them are on one line.
Lines ,
,
,
,
,
are the lines going through pairs of these points.
The angles that can be named using A, B, C, D are ∠ABC, ∠ABD, ∠DBC, ∠BCD, ∠BCA, ∠DCA, ∠BAD, ∠BAC, ∠DAC, ∠ADC, ∠ADB and ∠BDC.
Figure it Out (Page 23):
1. Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?
Answer:
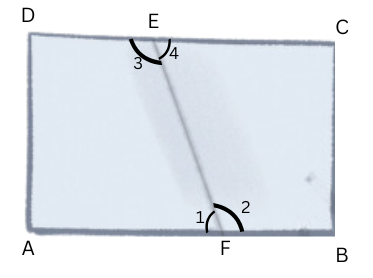
Angles formed between the fold and the sides of the paper are ∠AFE (marked by 1), ∠BFE (marked by 2), ∠DEF (marked by 3) and ∠CEF (marked by 4).
In the figure shown above, ∠DEF and ∠BFE are the largest angles and ∠AFE and ∠CEF are the smallest angles.
2. In each case, determine which angle is greater and why.
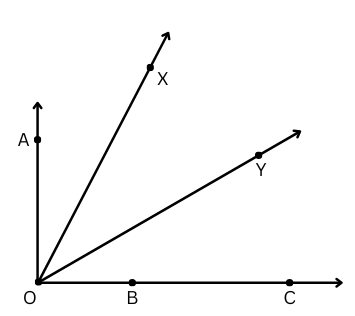
a. ∠AOB or ∠XOY
b. ∠AOB or ∠XOB
c. ∠XOB or ∠XOC
Discuss with your friends on how you decided which one is greater.
Answer:
a. ∠AOB > ∠XOY because ∠XOY occupies only a portion of the space of ∠AOB.
b. ∠AOB > ∠XOB. The ray turns more than the ray
, starting from the same initial ray
.
c. ∠XOB = ∠XOC because they are exactly superimposable.
3. Which angle is greater: ∠XOY or ∠AOB? Give reasons.
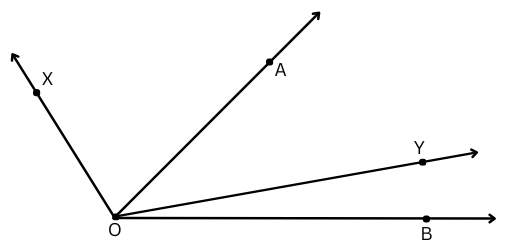
Answer:
It is easy to see that ∠XOA opens wider than ∠YOB. Hence, ∠XOA < ∠YOB.
If we add ∠AOY to ∠XOA we get ∠XOY.
If we add same angle ∠AOY to ∠YOB we get ∠AOB.
Therefore, we can say that ∠XOY > ∠AOB.
Figure it Out (Page 29):
1. How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?
Answer:
The classroom window shown below contains 16 right angles.
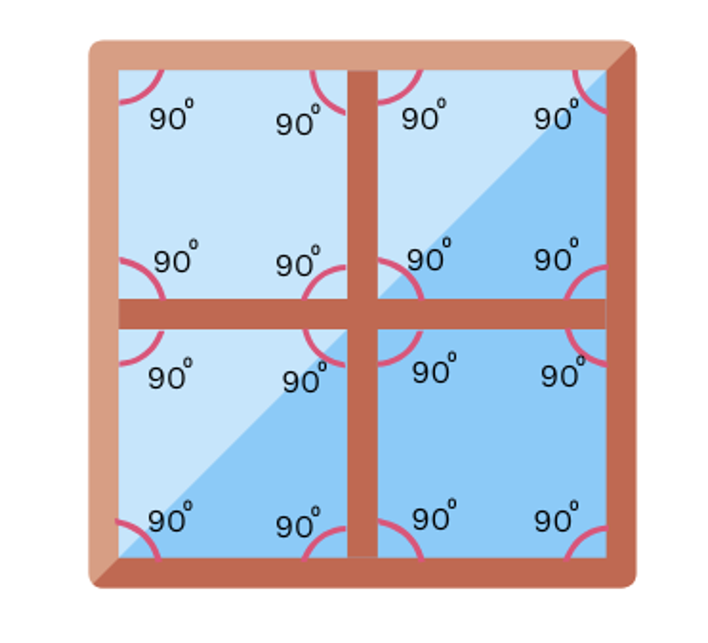
Other right angles in the classroom can be seen in doors, tables, chairs, blackboard, ruler, geometry box, pencil box, notebook etc.
2. Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?
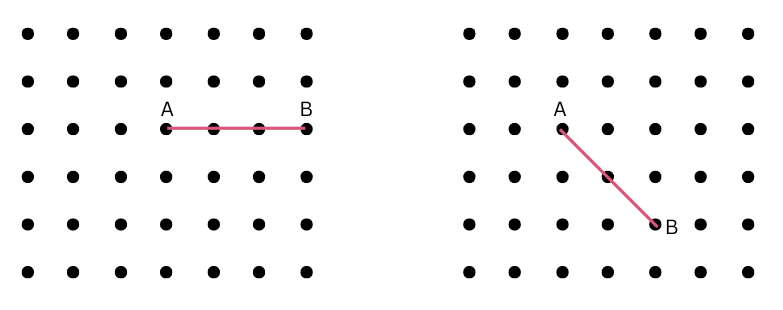
Answer:
The different ways of joining A to other grid points in the figure by a straight line to get a straight angle are shown below:


The point of this exercise was to show you that the straight angle will not change depending on the length of the line.
3. Now join A to other grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?
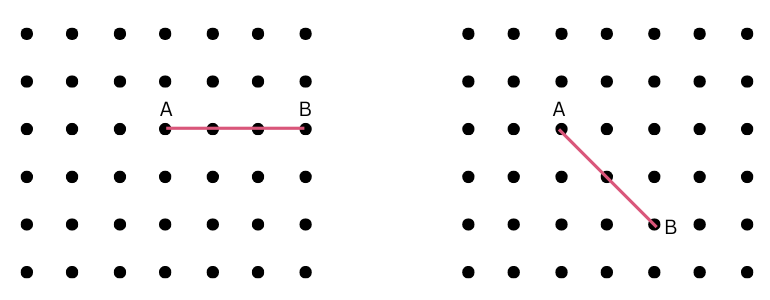
Hint: Extend the line further as shown in the figure below. To get a right angle at A, we need to draw a line through it that divides the straight angle CAB into two equal parts.
Answer:
Let us draw a line through it that divides the straight angle CAB into two equal parts.
All the different ways of joining A to other grid points in the figure by a straight line to get a right angle are shown below:
For grid on the left:
For grid on the right:
4. Get a slanting crease on the paper. Now, try to get another crease that is perpendicular to the slanting crease.
a. How many right angles do you have now? Justify why the angles are exact right angles.
b. Describe how you folded the paper so that any other person who doesn’t know the process can simply follow your description to get the right angle.
Answer:
a. We have four right angles: ∠AOB, ∠BOC, ∠COD, ∠AOD as shown below:
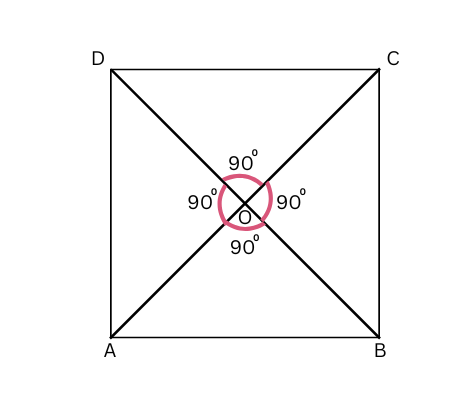
We can justify that ∠AOD and ∠COD by folding the paper along OD and matching end A with end C.
∠AOD and ∠COD are exactly superimposable. Hence, ∠AOD = ∠COD.
However, ∠AOC is a straight angle = 180o.
Since ∠AOD and ∠COD are equal and together form straight angle ∠AOC, we can say that ∠AOD = ∠COD = 90o.
Similarly, we can prove that ∠AOB and ∠COB are right angles.
b. The following folding process was followed to get the right angles:
- A square piece of paper was chosen for convenience.
- It is folded such that the first corner and the third corner (going anticlockwise) match.
- It is then opened and folded again such that the second corner and the fourth corner (going anticlockwise) match.
- Following this process, we get four right angles at the centre of the square.
Figure it Out (Page 31):
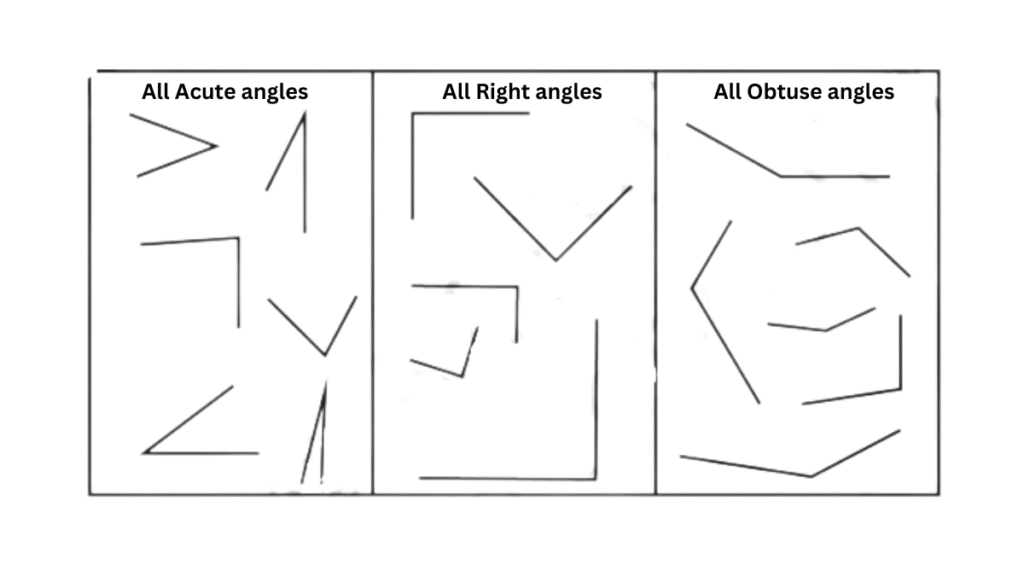
1. Identify acute, right, obtuse and straight angles in the previous figures.
Answer:
The acute, right and obtuse angles are shown in the previous figures:
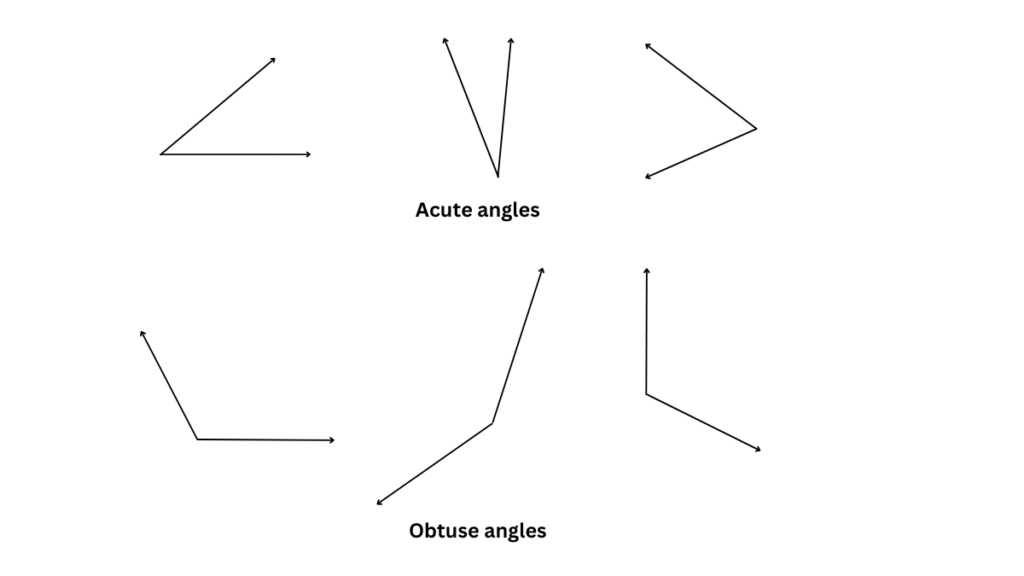
2. Make a few acute angles and a few obtuse angles. Draw them in different orientations.
Answer:
A few acute angles and a few obtuse angles drawn in different orientations are shown below:
3. Do you know what the words acute and obtuse mean? Acute means sharp and obtuse means blunt. Why do you think these words have been chosen?
Answer:
An acute angle is less than 90°, which makes it look sharp and narrow, like the point of a knife or a needle. Hence it is called acute, which means ‘sharp’.
An obtuse angle is more than 90° but less than 180°, giving it a wide, open, and rounded appearance. Hence it is called obtuse, which means ‘blunt’.
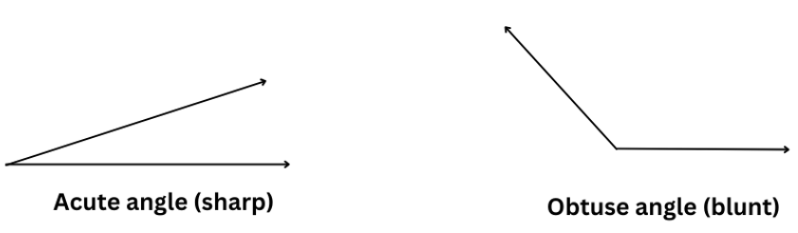
4. Find out the number of acute angles in each of the figures below.
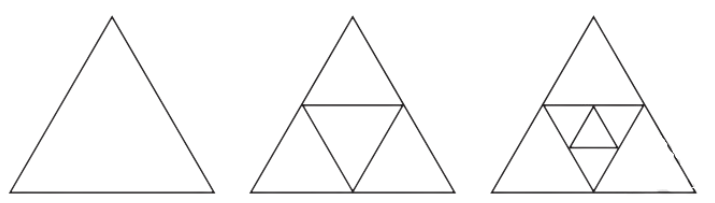
What will be the next figure and how many acute angles will it have? Do you notice any pattern in the numbers?
Answer:
The next figure is shown below to extreme right. It will have 30 acute angles.
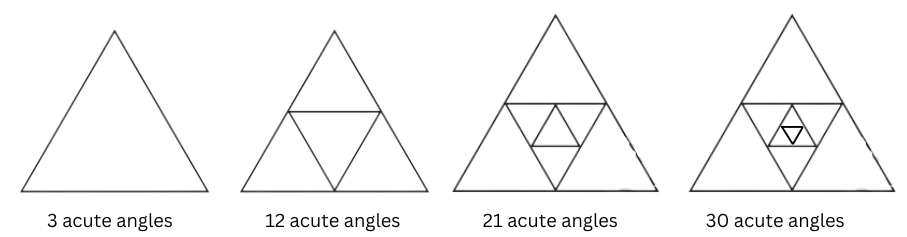
The pattern in the numbers is that each successive number increases by 9.
Figure it Out (Page 40):
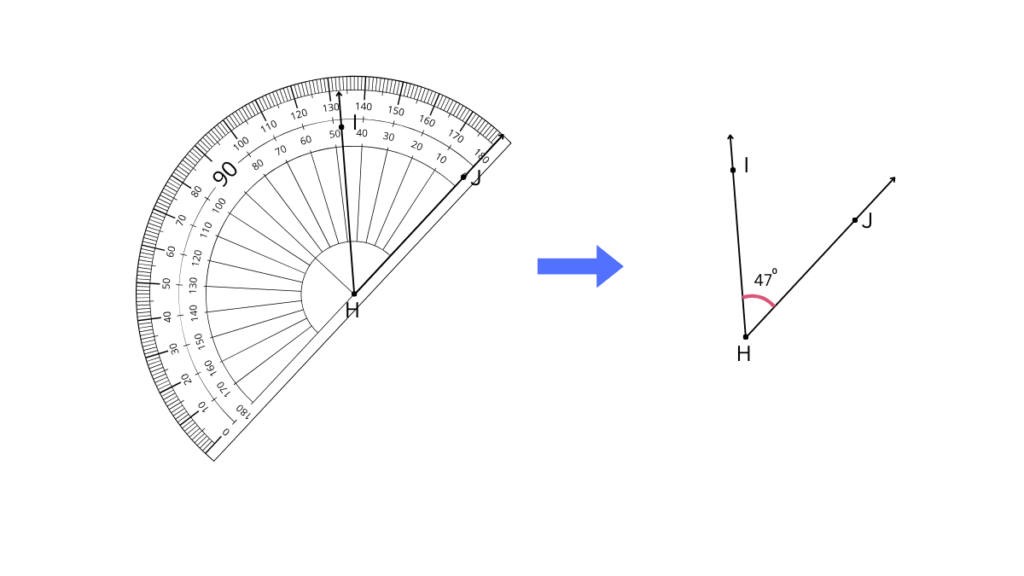
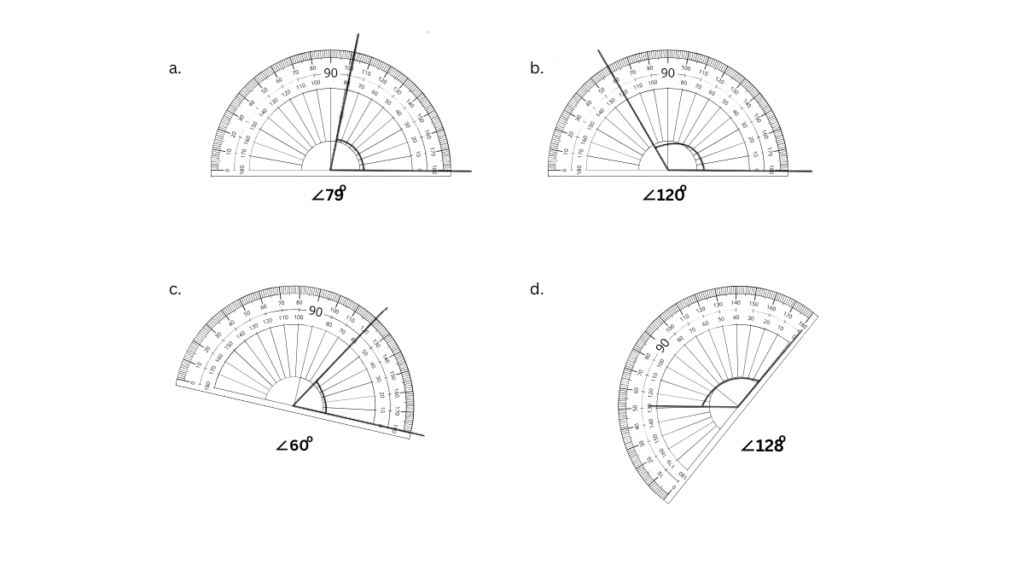
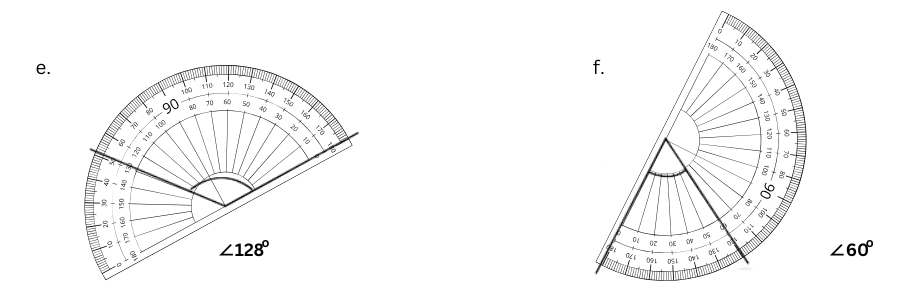
1. Find the degree measures of the following angles using your protractor.
Answer:
The first angle can be measured to be 47o as shown below:
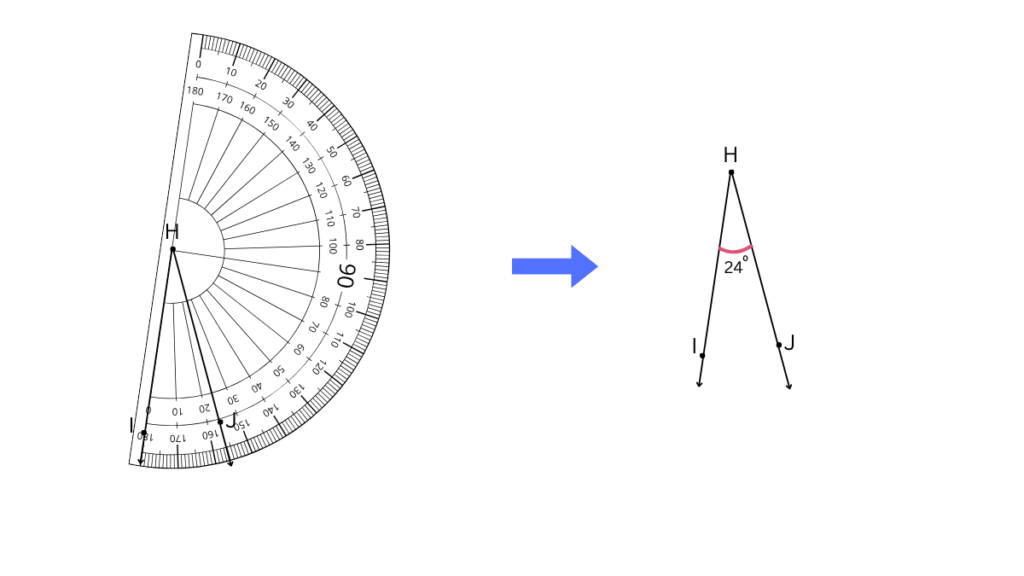
The second angle can be measured to be 24o as shown below:
The third angle can be measured to be 110o as shown below:
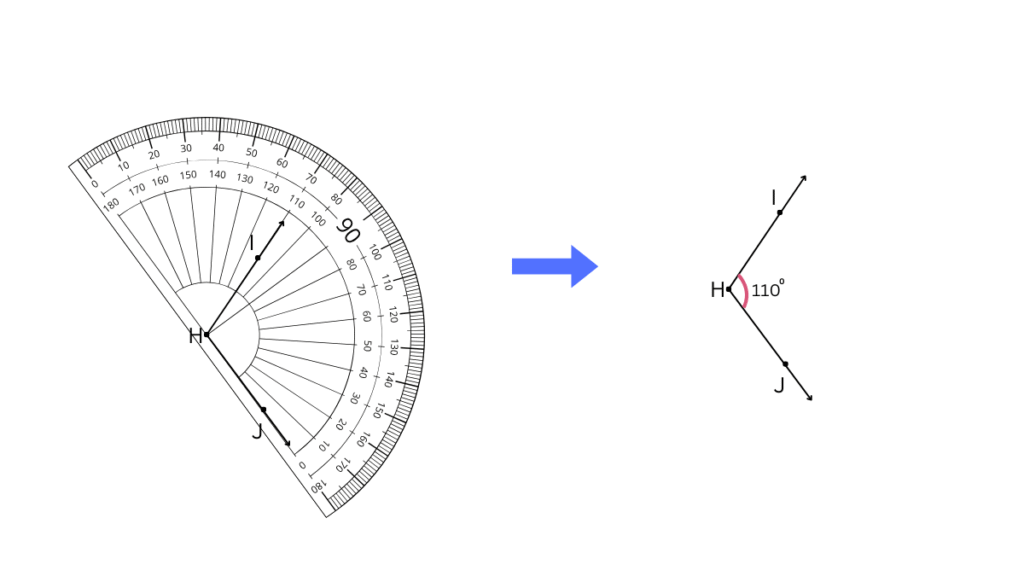
2. Find the degree measures of different angles in your classroom using your protractor.
Answer:
The degree measures of different angles in my classroom using the protractor are shown below:
Window pane: 90o
Edges of blackboard: 90o
Angles between blades of 3-bladed fan: 120o
Slanting desk: 10o
Window slightly opened: 10o
Some similar examples are shown below:
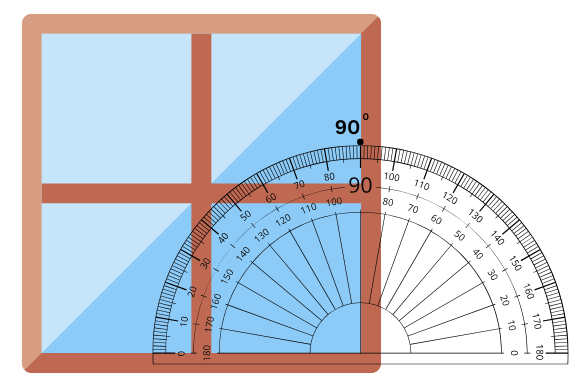
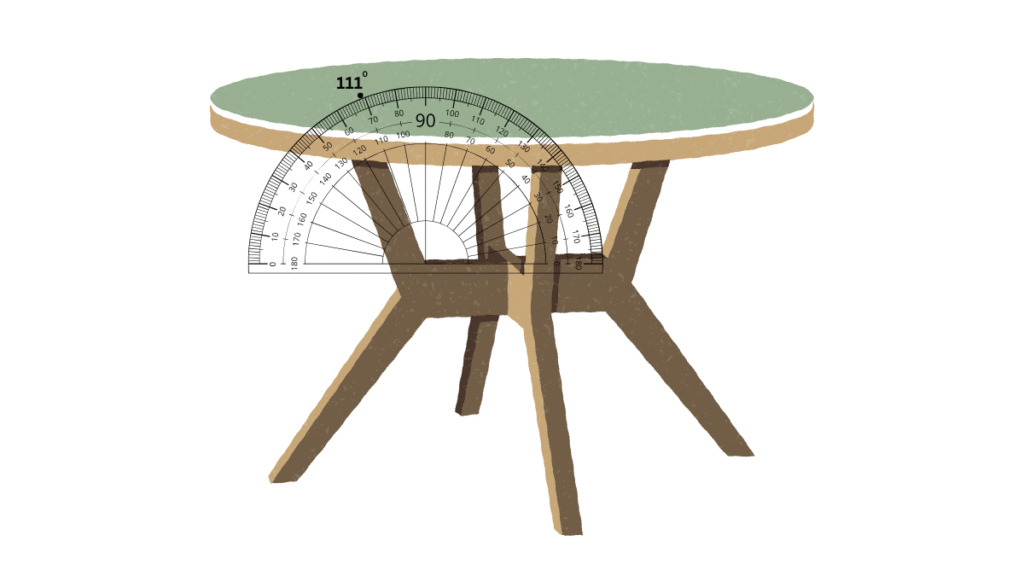
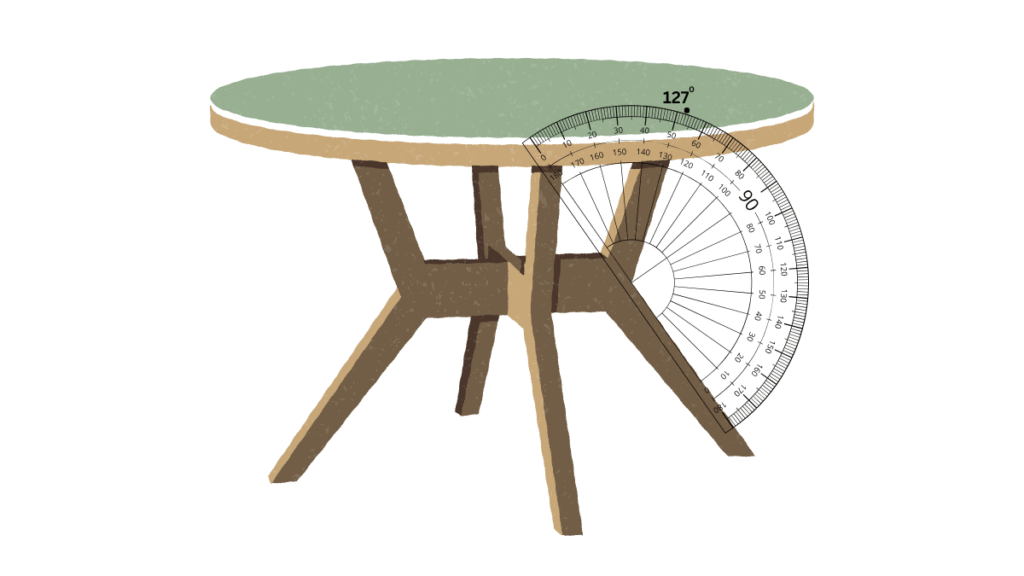
3. Find the degree measures for the angles given below. Check if your paper protractor can be used here!
Answer:
The first angle can be measured as 42o as shown below:

The second angle can be measured as 118o as shown below:

4. How can you find the degree measure of the angle given below using a protractor?
Answer:
- For convenience measure the smaller angle with the help of a protractor. The angle is found to be 101o.
- The bigger angle can be found by subtracting the smaller angle from 360o as shown: 360o – 101o = 259o.

5. Measure and write the degree measures for each of the following angles:

Answer:
6. Find the degree measures of ∠BXE, ∠CXE, ∠AXB and ∠BXC.
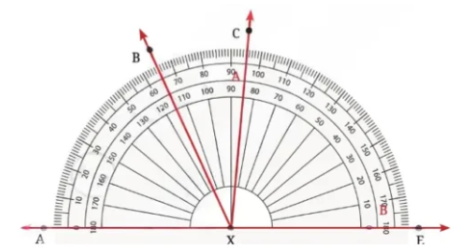
Answer:
∠BXE = 115o
∠CXE = 85o
∠AXB = 65o
∠BXC = ∠AXC – ∠AXB = 95o – 65o = 30o
7. Find the degree measures of ∠PQR, ∠PQS and ∠PQT.
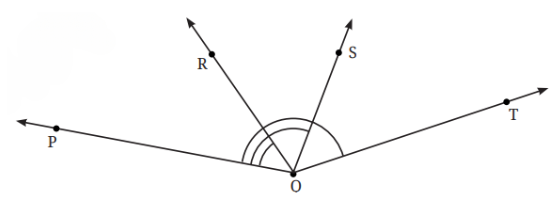
Answer:
We place the center of the protractor on the vertex Q. Align the protractor so that the arm passes through the 180º mark as in the picture below.
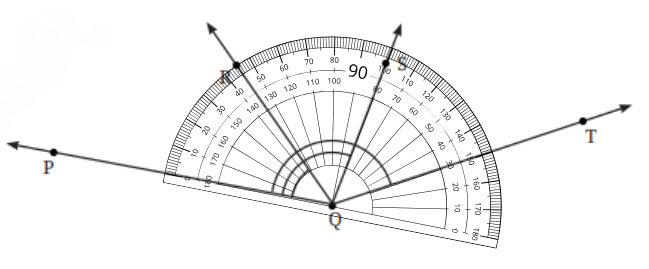
∠PQR = 45o
∠PQS = 100o
∠PQT = 150o
8. Make the paper craft as per the given instructions. Then, unfold and open the paper fully. Draw lines on the creases made and measure the angles formed.
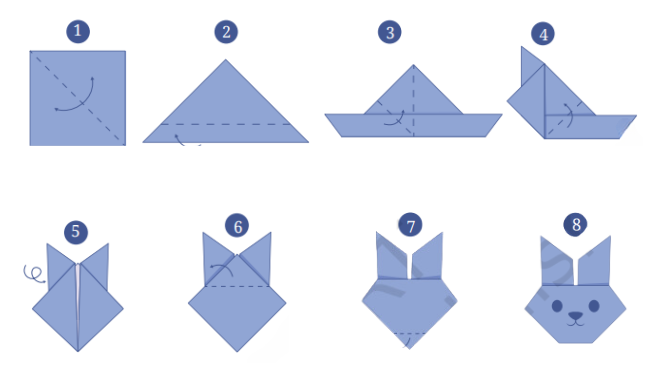
Answer:
Have fun doing this activity by yourself.
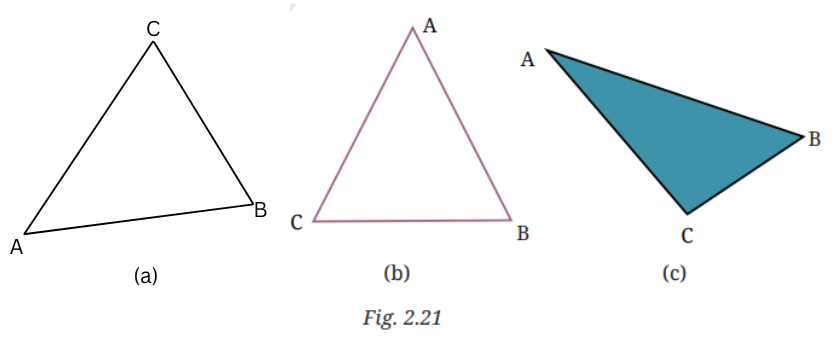
9. Measure all three angles of the triangle shown in Fig. 2.21 (a), and write the measures down near the respective angles. Now add up the three measures. What do you get? Do the same for the triangles in Fig. 2.21 (b) and (c). Try it for other triangles as well, and then make a conjecture for what happens in general! We will come back to why this happens in a later year.
Answer:
For triangle (a) in Fig. 2.21:
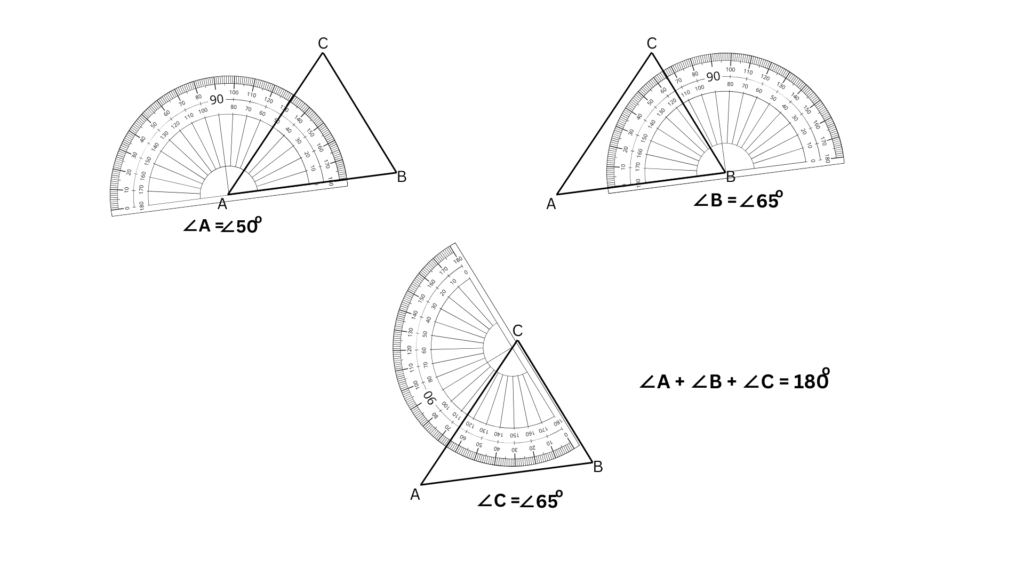
For triangle (b) in Fig. 2.21:
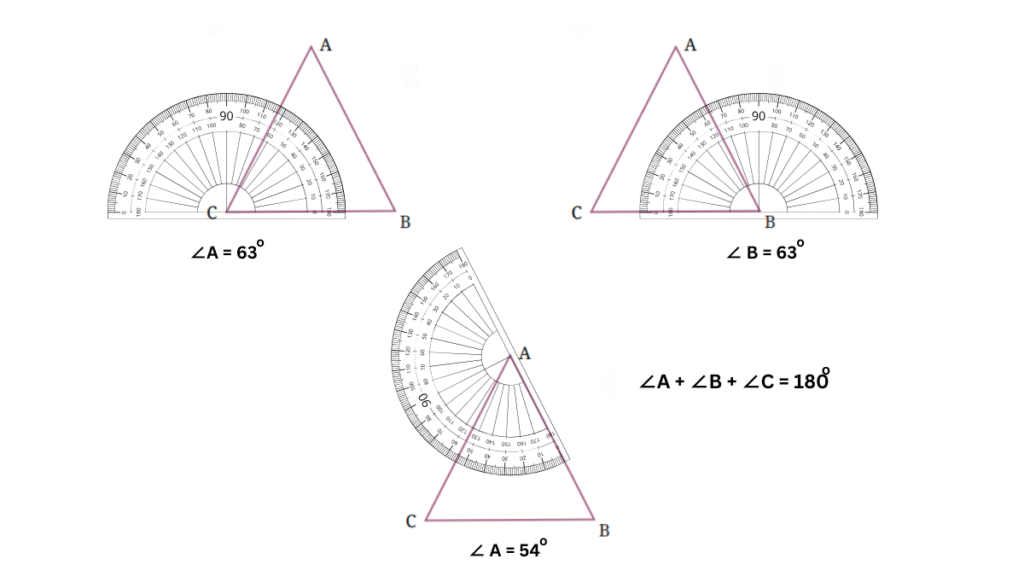
For triangle (c) in Fig. 2.21:
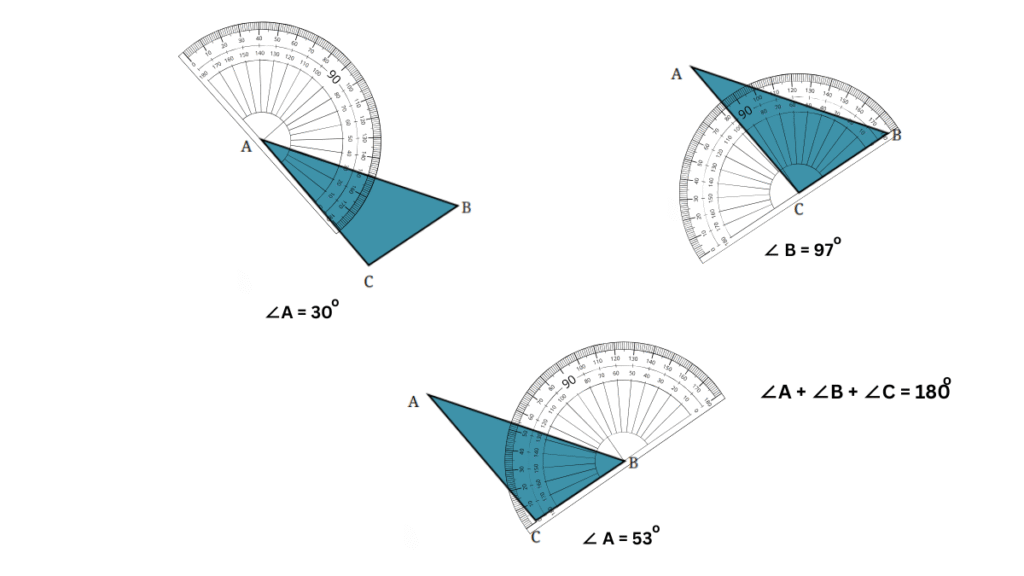
The angles of each triangle sum up to 180o. I tried it out for several other triangles and the result was the same.
Thus, we can make a conjecture that sum of angles in a triangle = 180o.
Figure it Out (Page 45):
Where are the angles?
1. Angles in a clock:
a. The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?

b. What will be the angle at 2 o’clock? And at 4 o’clock? 6 o’clock?
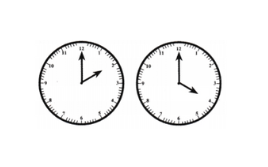
c. Explore other angles made by the hands of a clock.
Answer:
In the clock, there are 12 numbers spread out over an angle of 360o. We can say that the clock is divided into 12 parts by the numbers.
a. 1 o’clock represents 1 part.
Therefore, the angle between the hands at 1 o’clock = 360o/12 = 30o.
b. 2 o’clock represents 2 parts.
Therefore, the angle between the hands at 2 o’clock = (360o/12) × 2 = 60o.
4 o’clock represents 4 parts.
Therefore, the angle between the hands at 4 o’clock = (360o/12) × 4 = 120o.
4 o’clock represents 4 parts.
Therefore, the angle between the hands at 6 o’clock = (360o/12) × 6 = 180o.
c. The angle made by the hands at 8 o’clock = (360o/12) × 8 = 240o.
The angle at made by the hands at 5 o’clock = (360o/12) × 5 = 150o.
The angle made by the hands of the clock after one complete rotation = (360o/12) × 12 = 360o.
2. The angle of a door:
Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle and what will be the arms of the angle?

Answer:
Yes, it is possible to express the amount by which a door is opened using an angle.
The vertex of the angle will be the hinge of the door, one arm will along the door and the other arm will be along the open doorway as shown below:

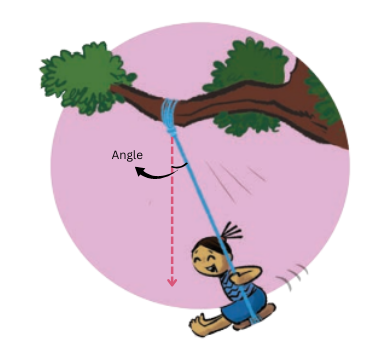
3. Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle?

Answer:
We draw a line vertically downwards from the point of attachment of the rope with the tree. The angle is shown below:
4. Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs? What are the arms of each angle? Which arm is visible and which is not?

Answer:
Yes, angles be used to describe the slopes of the slabs.
One arm of the angles is along the slope and the other is horizontal as shown below:

The arm of the angle along the slope is visible, but the angle along the horizontal is not visible.
Note: You will find that the steeper the slope, the faster the ball rolls. In this case, the slope at the top is the steepest when compared with the horizontal, which makes the top angle the steepest. Hence, the ball will roll down fastest along the top slope.
5. Observe the images below where there is an insect and its rotated version. Can angles be used to describe the amount of rotation? How? What will be the arms of the angle and the vertex?
Hint: Observe the horizontal line touching the insects.

Answer:
Yes, angles can be used to describe the amount of rotation of the insects.
For each insect, one arm of the angle must be along the bottom portion of the insect while it is horizontal. The other arm of the angle must be along the bottom portion of the insect while it is vertical. The two arms meet at the vertex of the angle. These are shown below:

The angle in both cases can be measured to be 90o.
The insect on the left was rotated counterclockwise 90o from horizontal to vertical position.
The insect on the right was rotated clockwise 90o from horizontal to vertical position.
Figure it Out (Page 49):
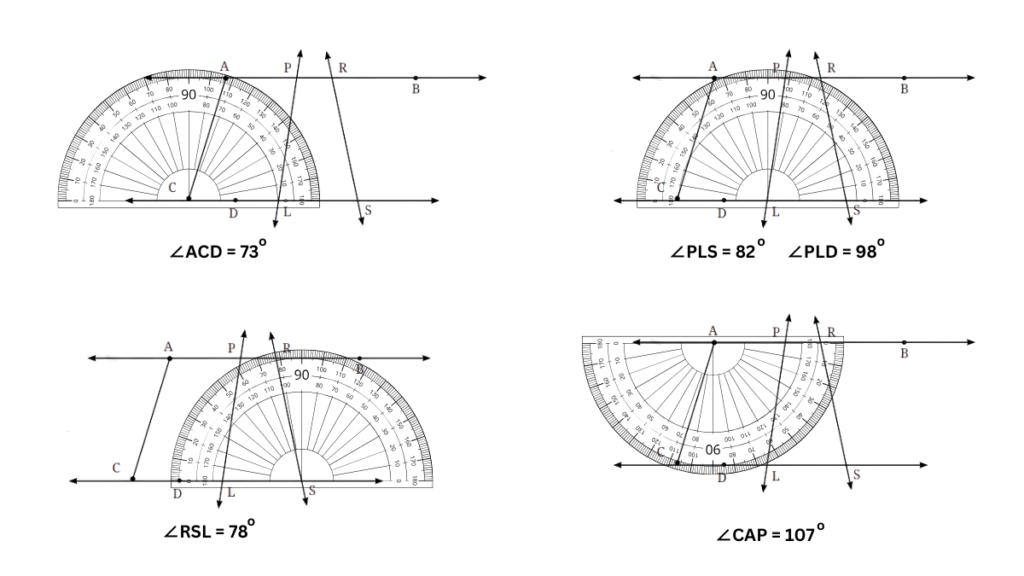
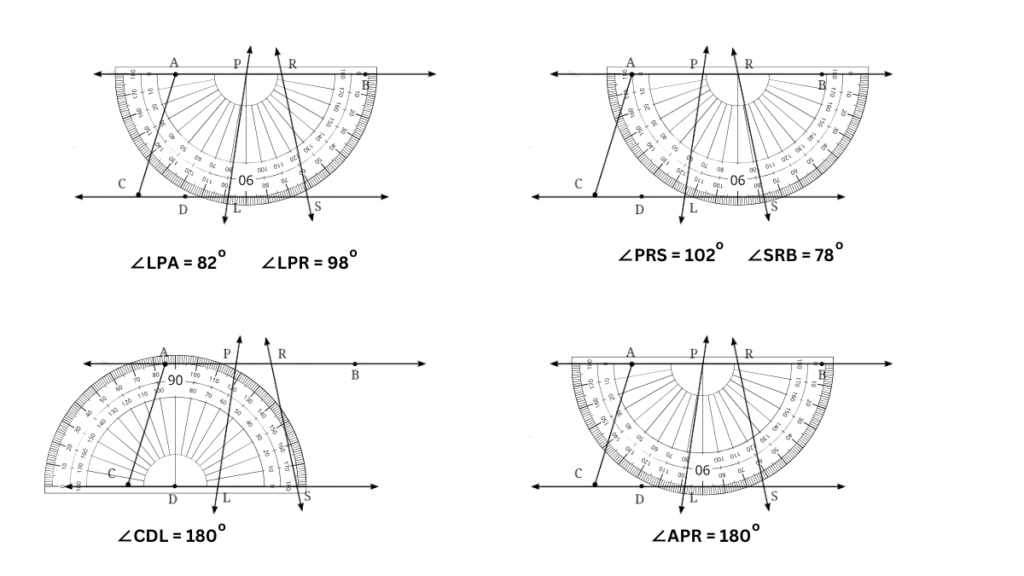
1. In Fig. 2.23, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.
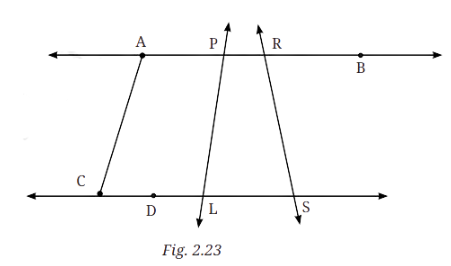
Answer:
The estimated values of all the different angles and their actual values measured with a protractor are recorded in the table below:
| Angle | Guessed Value | Actual Values |
| ∠ACD | 70o | 73o |
| ∠PLS | 80o | 82o |
| ∠PLD | 100o | 98o |
| ∠RSL | 80o | 78o |
| ∠CAP | 105o | 107o |
| ∠LPA | 80o | 82o |
| ∠LPR | 100o | 98o |
| ∠PRS | 100o | 102o |
| ∠SRB | 80o | 78o |
| ∠CDL | 180o | 180o |
| ∠APR | 180o | 180o |
Each of the angles were measured using a protractor as shown below:
2. Use a protractor to draw angles having the following degree measures:
a. 110° b. 40° c. 75° d. 112° e. 134°
Answer:
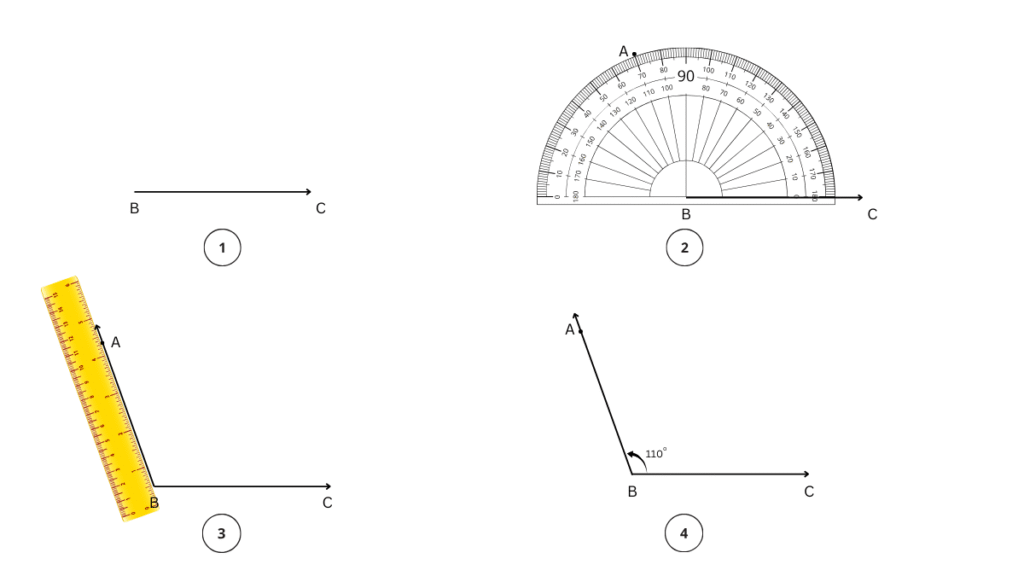
a. 110°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on B and align BC to the 0 line.
Step 3: Now, starting from 0, count your degrees (0, 10, 30) up to 110o on the protractor. Mark point A at the label 110°.
Step 4: Using a ruler join the point B and A. ∠ABC = 110° is the required angle.
b. 40°
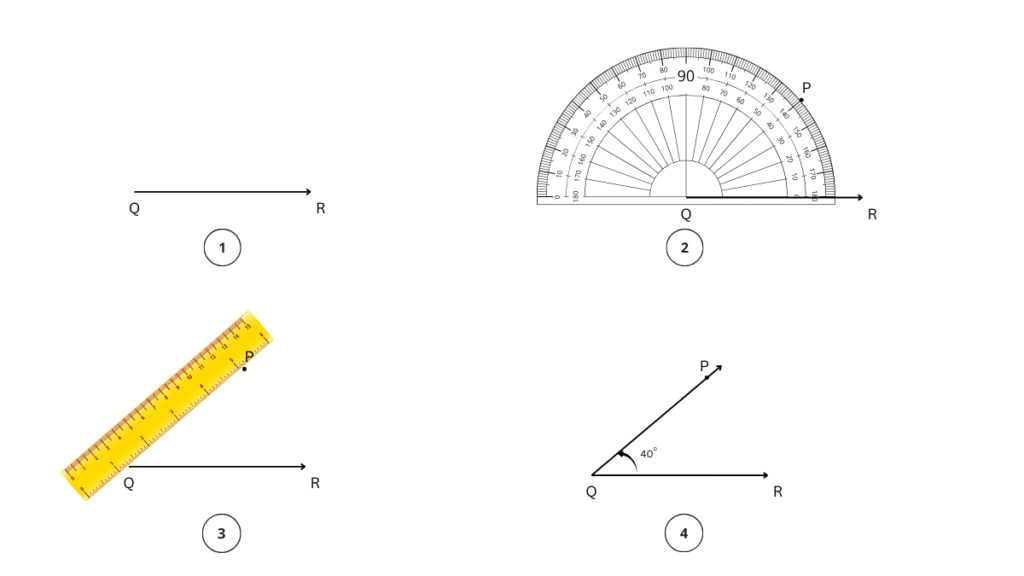
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on Q and align QR to the 0 line.
Step 3: Now, starting from 0, count your degrees (0, 10, 30) up to 40o on the protractor. Mark point P at the label 40°.
Step 4: Using a ruler join the point Q and P. ∠PQR = 40° is the required angle.
c. 75°
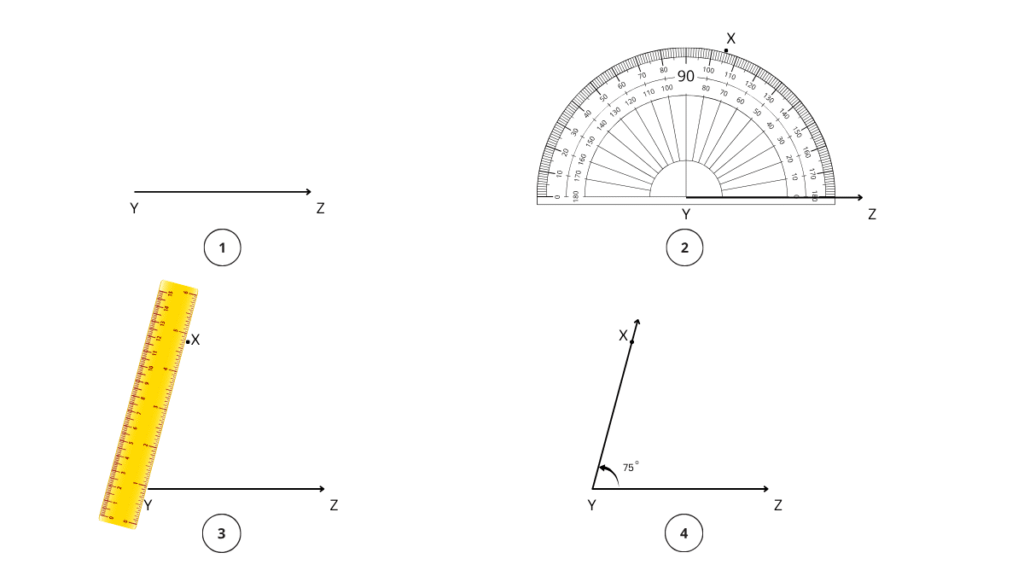
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on Y and align YZ to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 75o on the protractor. Mark point X at the label 75°.
Step 4: Using a ruler join the point Y and X. ∠XYZ = 75° is the required angle.
d. 112°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on M and align MN to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 112o on the protractor. Mark point L at the label 112°.
Step 4: Using a ruler join the point M and L. ∠LMN = 112° is the required angle.
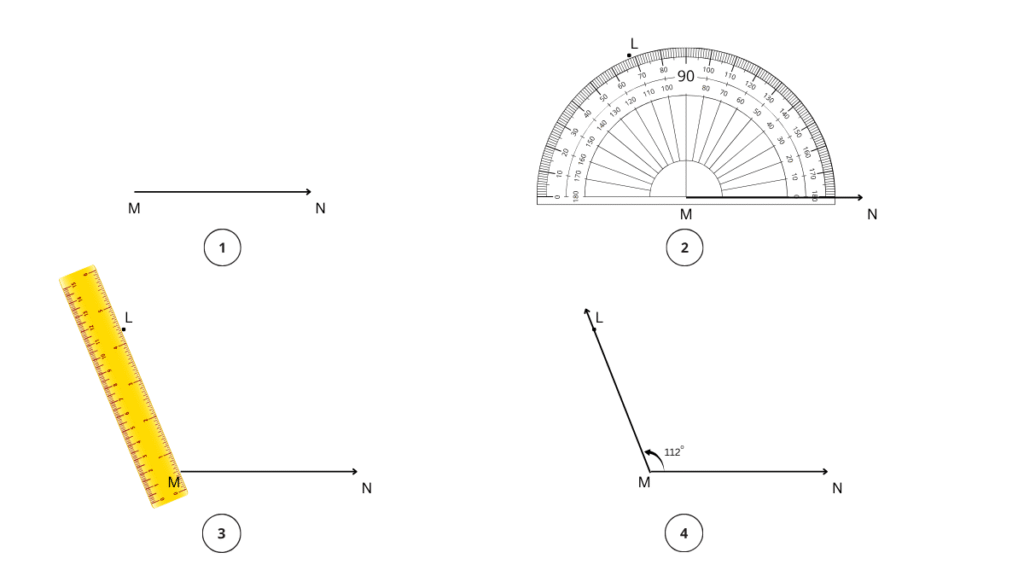
e. 134°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on E and align EF to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 134o on the protractor. Mark point D at the label 134°.
Step 4: Using a ruler join the point E and D. ∠DEF = 134° is the required angle.

3. Draw an angle whose degree measure is the same as the angle given below:
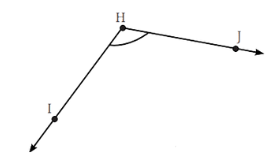
Also, write down the steps you followed to draw the angle.
Answer:
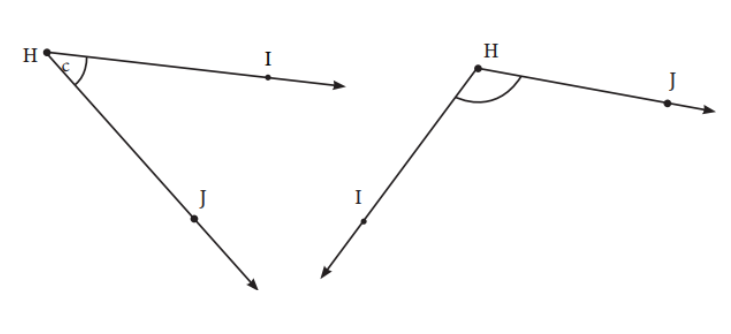
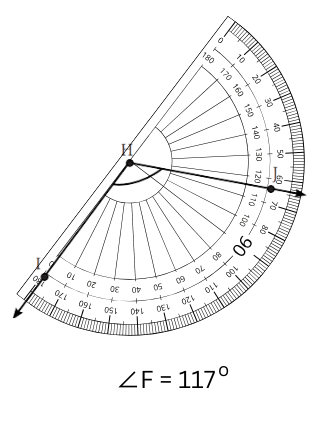
First, we measure the ∠JHI. The following steps were followed:
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on H and align HI to the 0 line.
Step 3: Now, starting from 0, count the degrees where meets the dial of the protractor.
Step 4: Read the measure of ∠JHI = 117o.
Secondly, we draw the ∠ABC with the same measure.
Step 5: We begin with the base and draw .
Step 6: We will place the centre point of the protractor on B and align BC to the 0 line.
Step 7: Now, starting from 0, count your degrees up to 117o on the protractor. Mark point A at the label 117°.
Step 8: Using a ruler join the point B and A. ∠ABC = 117° is the required angle.
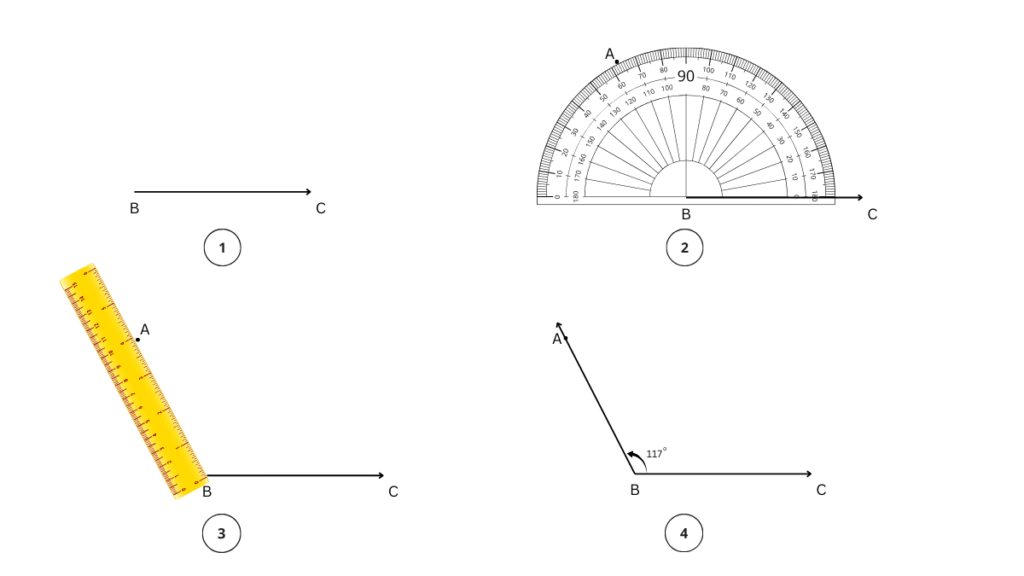
Figure it Out (Page 51):
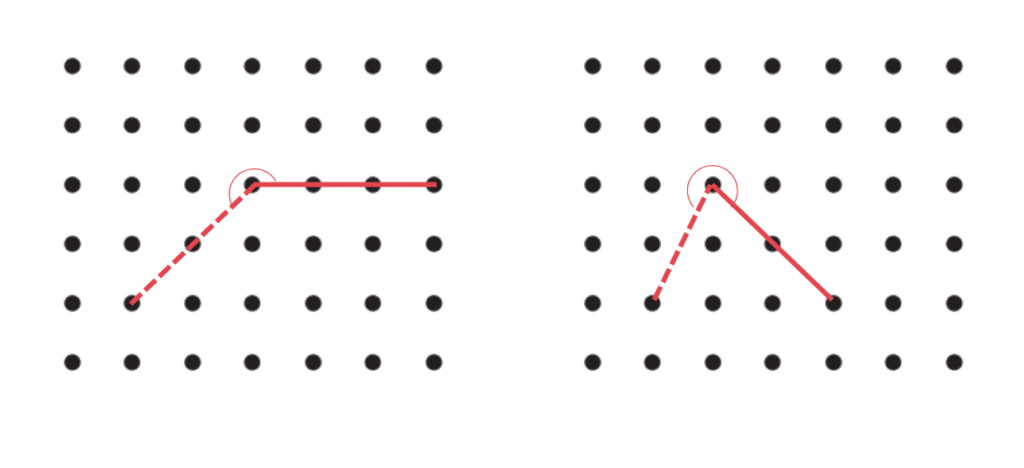
1. In each of the below grids, join A to other grid points in the figure by a straight line to get:
a. An acute angle

b. An obtuse angle
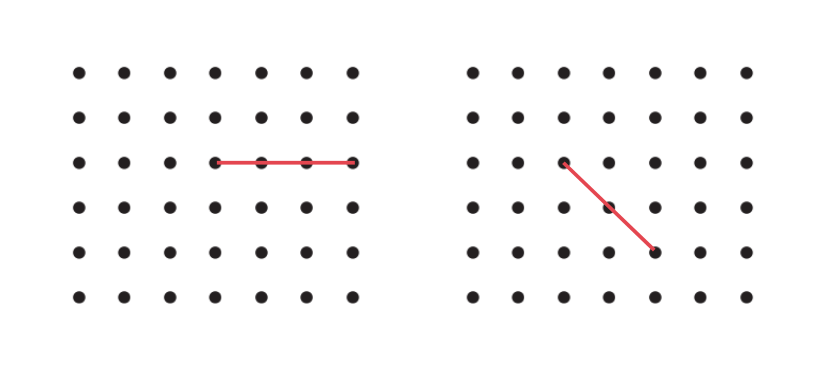
c. A reflex angle
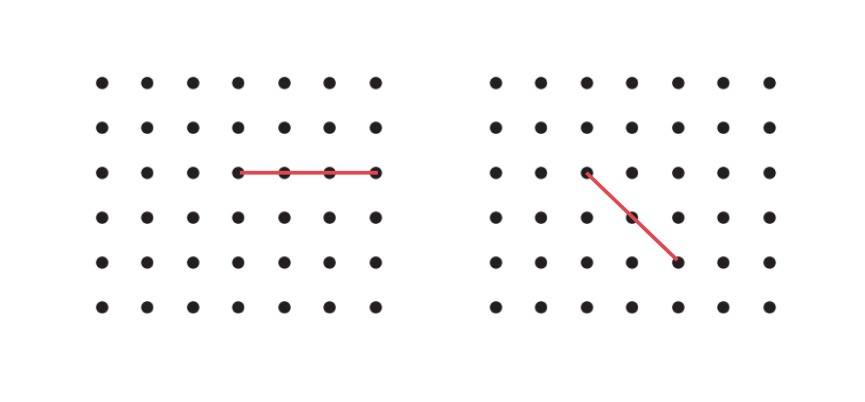
Mark the intended angles with curves to specify the angles. One has been done for you.
Answer:
a. An acute angle
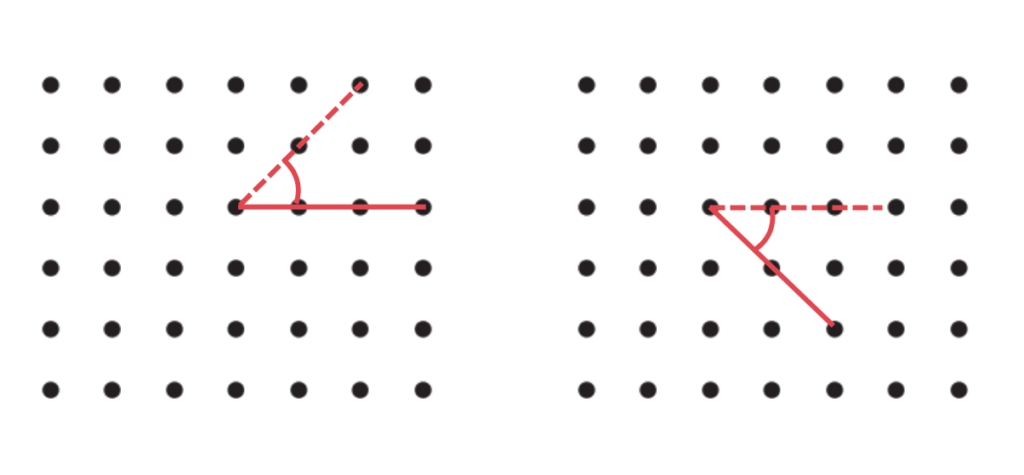
b. An obtuse angle
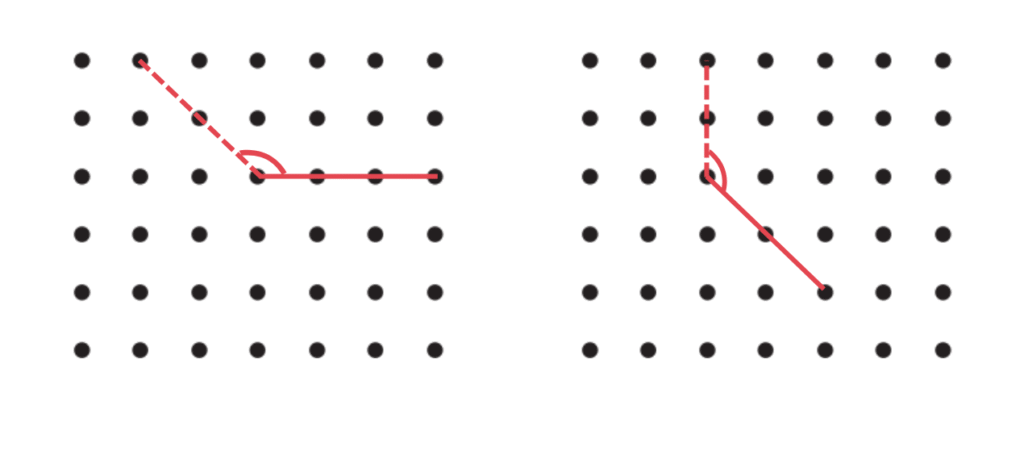
c. A reflex angle
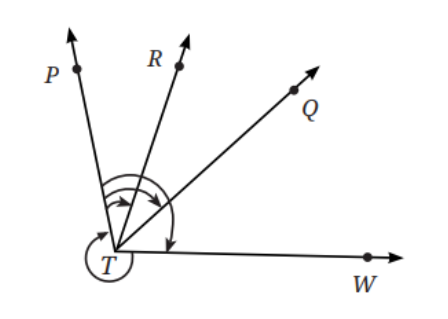
2. Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.
a. ∠PTR b. ∠PTQ c. ∠PTW d. ∠WTP
Answer:
We follow the below steps:
Step 1: We will place the centre point of the protractor on T and align TP to the outer 0 line.
Step 2: Read off the values for ∠PTR, ∠PTQ, ∠PTW, ∠WTP.
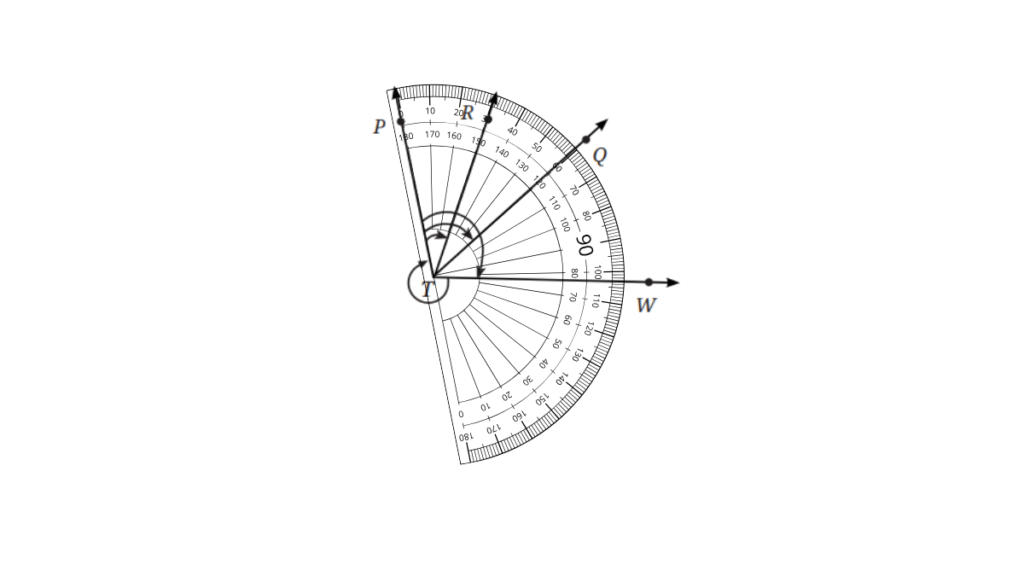
We get,
(a) ∠PTR = 30o. Therefore, it is an acute angle.
(b) ∠PTQ = 60o. Therefore, it is an acute angle.
(c) ∠PTW = 103o. Therefore, it is an obtuse angle.
(d) ∠WTP = 360o – 103o = 257o. Therefore, it is a reflex angle.
Figure it Out (Page 53):
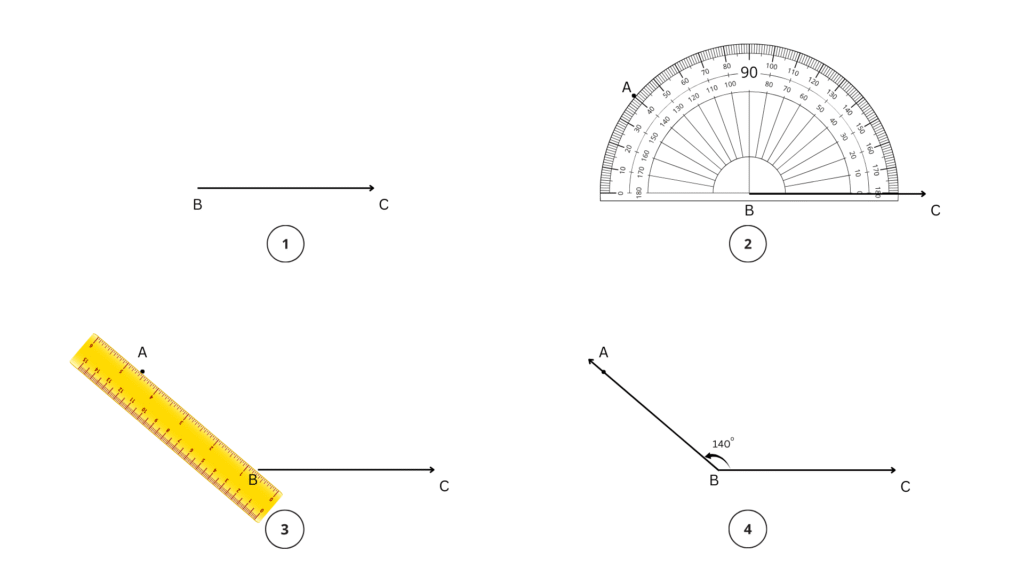
1. Draw angles with the following degree measures:
a. 140° b. 82° c. 195° d. 70° e. 35°
Answer:
a. 140°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on B and align BC to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 140o on the protractor. Mark point A at the label 140°.
Step 4: Using a ruler join the points A and B. ∠ABC = 140° is the required angle.
b. 82°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on Q and align QR to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 82o on the protractor. Mark point P at the label 82°.
Step 4: Using a ruler join the points P and Q. ∠ABC = 82° is the required angle.
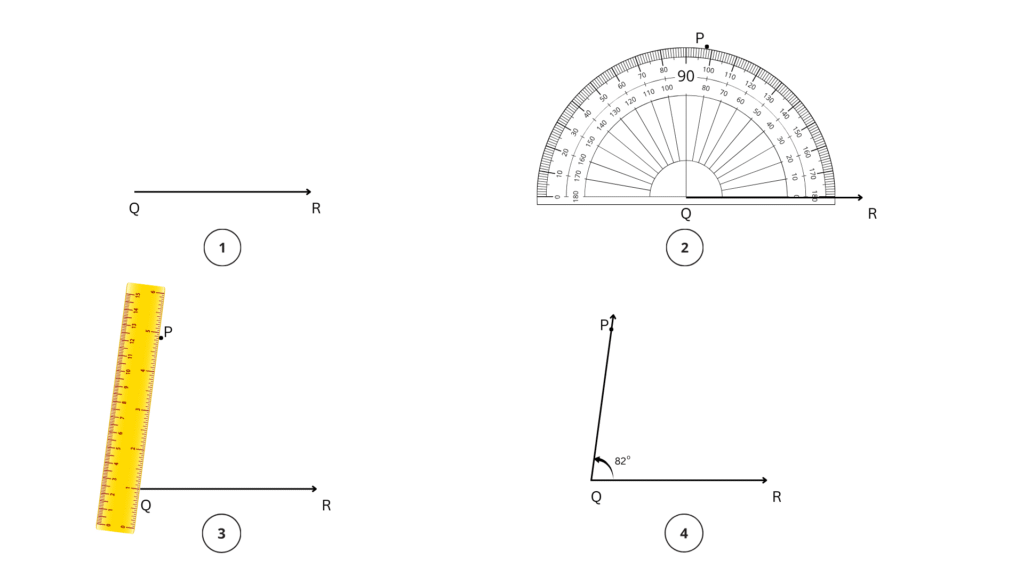
c. 195°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the inverted protractor on M and align MN to the 0 line on the outer ring.
Step 3: Now, starting from 0, count your degrees up to 195o on the protractor. Mark point L at the label 195°.
Step 4: Using a ruler join the points M and L. ∠NML = 195° is the required angle.

d. 70°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on Y and align YZ to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 70o on the protractor. Mark point X at the label 70°.
Step 4: Using a ruler join the points X and Y. ∠ABC = 70° is the required angle.
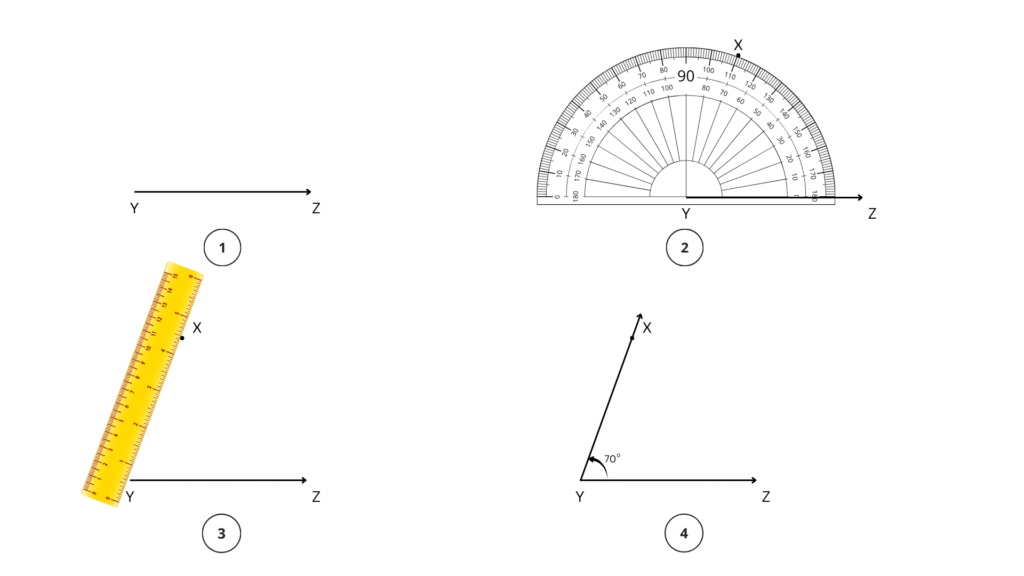
e. 35°
Step 1: We begin with the base and draw .
Step 2: We will place the centre point of the protractor on E and align EF to the 0 line.
Step 3: Now, starting from 0, count your degrees up to 35o on the protractor. Mark point D at the label 35°.
Step 4: Using a ruler join the points D and E. ∠DEF = 35° is the required angle.
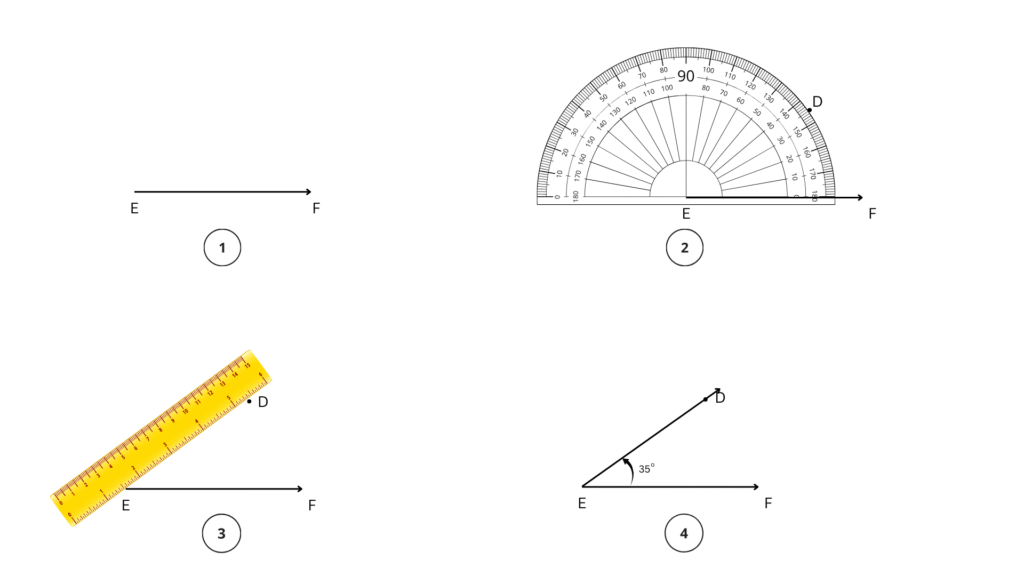
2. Estimate the size of each angle and then measure it with a protractor:

Classify these angles as acute, right, obtuse or reflex angles.
Answer:
The angles are measured using a protractor as shown below:
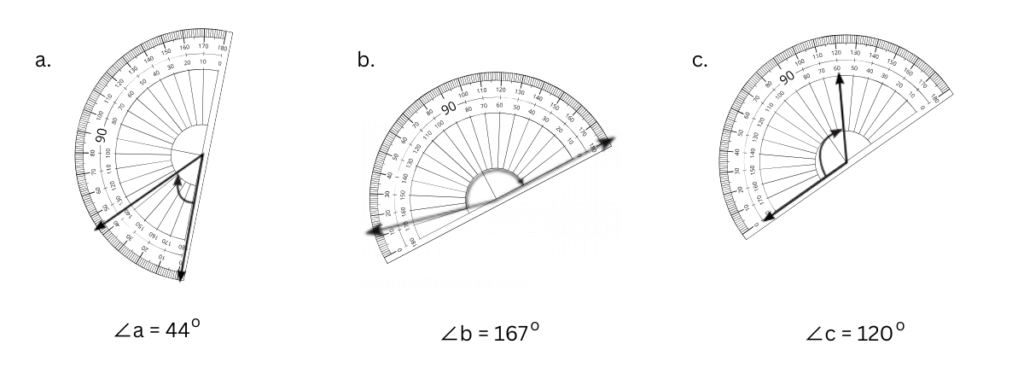

The estimated values of all the different angles and their actual values measured with a protractor are recorded in the table below:
| Angle | Estimated Value | Actual Value | Type of Angle |
| ∠a | 45o | 44o | Acute |
| ∠b | 170o | 167o | Obtuse |
| ∠c | 120o | 120o | Obtuse |
| ∠d | 30o | 32o | Acute |
| ∠e | 950 | 98o | Obtuse |
| ∠f | 350o | 349o | Reflex |
3. Make any figure with three acute angles, one right angle and two obtuse angles.
Answer:
In the figure below,
Acute angles: ∠AOC, ∠BOC, ∠COD
Right angle: ∠AOF
Obtuse angles: ∠DOE, ∠EOF
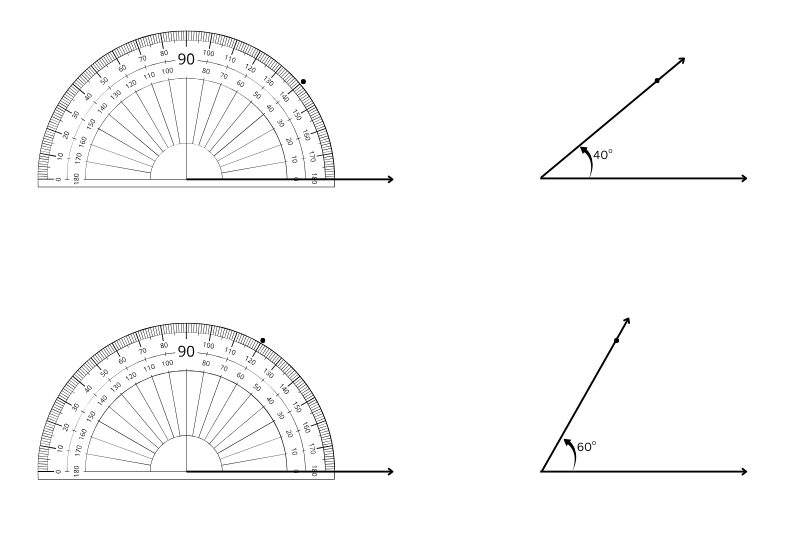
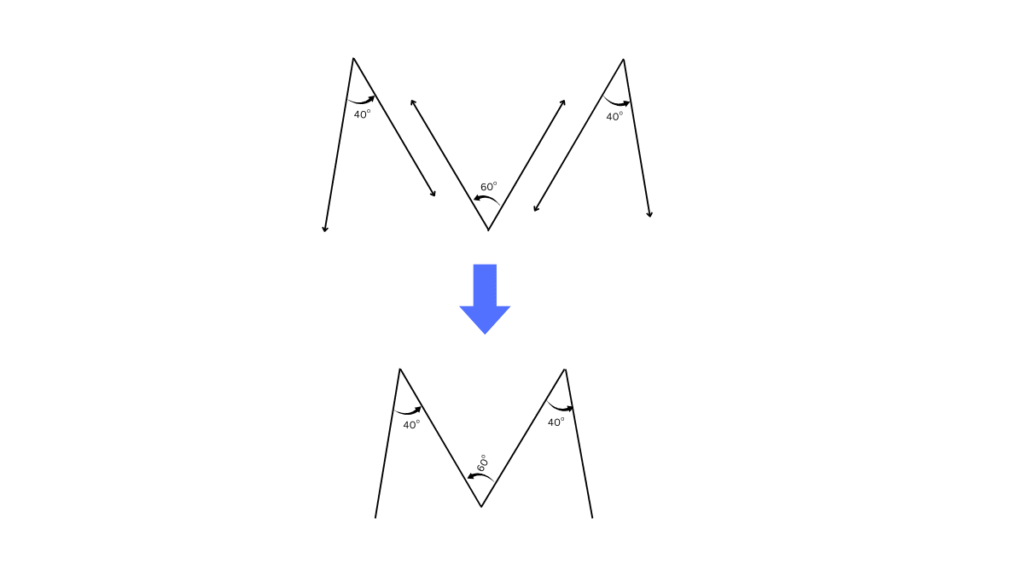
4. Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Answer:
First, we draw the angles 40o and 60o as shown below:
Then we realign them to form the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°, as shown below:
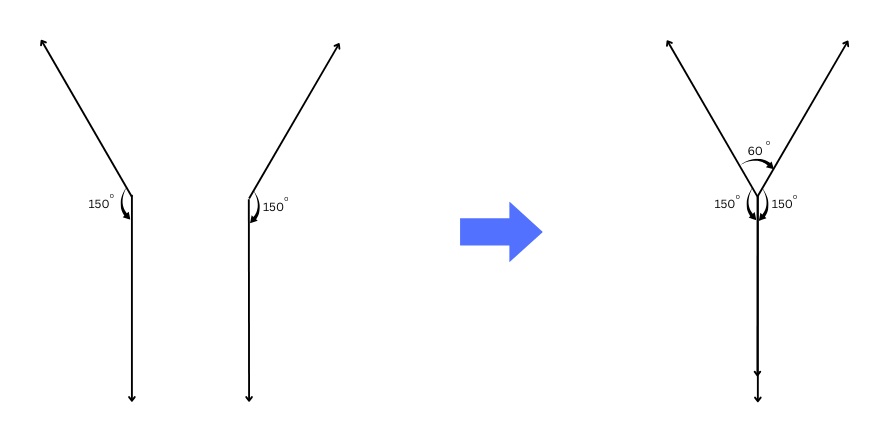
5. Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.
Answer:
First, we draw two 150o angles as shown below:
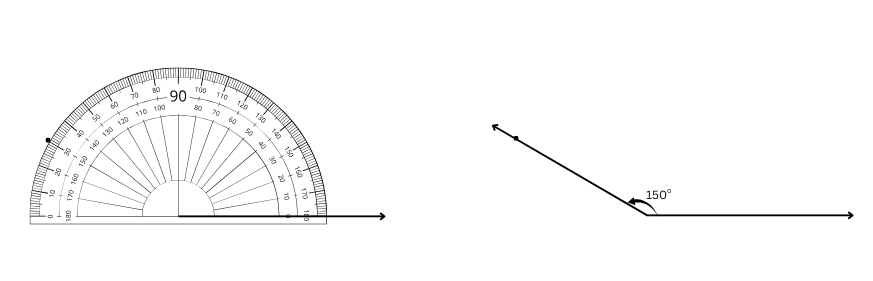
Then we realign the two 150o angles to draw the letter ‘Y’ as shown below:
6. The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?

Answer:
The 24 spokes in Ashoka Chakraare arranged in a circle.
The total angle in the centre is 360o.
There are 24 spokes in all forming an angle of 360o.
Therefore, the angle between any two spokes right next to each other = 360o/24 = 15o.
We observe that the largest acute angle formed between two spokes = 15o × 5 = 75o.
7. Puzzle: I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle measure. What are the possibilities for my measure?
Answer:
According to the problem,
If you double the measure of the acute angle, we get an acute angle.
If you triple the measure, we get an acute angle again.
If you quadruple the measure, we get an acute angle yet again.
If you multiply the acute angle by 5, you get an obtuse angle measure.
Therefore, we can write the following,
4 × acute angle < 90o
or, acute angle < 22 1/2o
5 × acute angle > 90o
or, acute angle > 18o
Therefore, the acute angle lies between 18o and 22 1/2o.
We can choose values such as 19o, 20o, 21o, 22o for the acute angle values.


