Figure it Out (Page 75):
Naresh and Navya decided to go to each student in the class and ask what their favourite game is. Then they prepared a list.
Navya is showing the list:
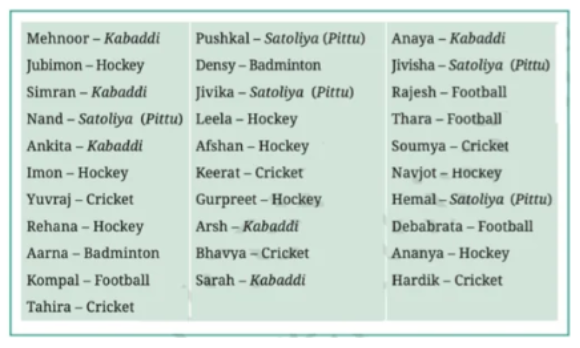
She says (happily), “I have collected the data. I can figure out the most popular game now!”
A few other children are looking at the list and wondering, “We can’t yet see the most popular game. How can we get it from this list?”
Answer:
To find the most popular game among Naresh’s and Navya’s classmates, we make a table with two columns. The column on the left will consist of the names of the games and the column on the right will consist of the number of times the games have been mentioned by the classmates. The game with the highest mentions will be the most popular game.
The required table is given below:
| Game | Number of Students |
| Kabaddi | 6 |
| Hockey | 7 |
| Satoliya (Pittu) | 5 |
| Cricket | 6 |
| Football | 4 |
| Badminton | 2 |
The advantage of this method is that it represents the data in a form that is easy to visualize.
We can easily see that the most popular game is hockey because it has been mentioned the maximum number of times (7 times).
Figure it Out (Page 75-76):
1. What would you do to find the most popular game among Naresh’s and Navya’s classmates?
Answer:
To find the most popular game among Naresh’s and Navya’s classmates, we make a table with two columns. The column on the left will consist of the names of the games and the column on the right will consist of the number of times the games have been mentioned. The game with the highest mentions will be the most popular game.
2. What is the most popular game in their class?
Answer:
The most popular game in their class is hockey because it has been mentioned 8 times.
3. Try to find out the most popular game among your classmates.
Answer:
To find out the most popular game among your classmates, you make a table with two columns. The column on the left will consist of the names of the games and the column on the right will consist of the number of times the games have been mentioned. The game with the highest mentions will be the most popular game.
The classmates’ responses were recorded using the procedure above and it was found that football was the favourite game.
4. Pari wants to respond to the questions given below. Put a tick (✓) for the questions where she needs to carry out data collection and put a cross (X) for the questions where she doesn’t need to collect data. Discuss your answers in the classroom.
a. What is the most popular TV show among her classmates?
b. When did India get independence?
c. How much water is getting wasted in her locality?
d. What is the capital of India?
Answer:
a. What is the most popular TV show among her classmates? ✓
Explanation: The preference of TV shows can vary among her classmates and people can have the same choices. Hence, data collection is needed.
b. When did India get independence? X
Explanation: This is a fixed number, so no data collection is needed.
c. How much water is getting wasted in her locality? ✓
Explanation: Data collection is needed to monitor the water getting wasted in her locality because it can happen from various sources.
d. What is the capital of India? X
Explanation: The capital of India is fixed, hence this situation does not need data collection.
Figure it Out (Page 76):
1. Complete the table to help Shri Nilesh to purchase the correct numbers of sweets:
• How many students chose jalebi? _______
• Barfi was chosen by _______ students?
• How many students chose gujiya? _______
• Rasgulla was chosen by _______ students?
• How many students chose gulab jamun? _______
Shri Nilesh requested one of the staff members to bring the sweets as given in the table. The above table helped him to purchase the correct numbers of sweets.
Answer:
• How many students chose jalebi? 6
• Barfi was chosen by _______ students? 3
• How many students chose gujiya? 13
• Rasgulla was chosen by 7 students?
• How many students chose gulab jamun? 9
2. Is the above table sufficient to distribute each type of sweet to the correct student? Explain. If it is not sufficient, what is the alternative?
Answer:
No, the above table is not sufficient to distribute each type of sweet to the correct student because it does not specify which particular student wants which particular sweet. The alternative is to add another column in the table which mentions the names of all the students who want a particular sweet, beside the name of that sweet.
Figure it Out (Page 77):
1. Help her to figure out the following –
• The largest shoe size in the class is _________
• The smallest shoe size in the class is _________
• There are _________ students who wear shoe size 5.
• There are _________ students who wear shoe sizes larger than 4.
Answer:
• The largest shoe size in the class is 7.
• The smallest shoe size in the class is 3.
• There are 10 students who wear shoe size 5.
• There are 15 students who wear shoe sizes larger than 4.
2. How did arranging the data in ascending order help to answer these questions?
Answer:
Arranging the data in ascending order helps to answer these questions in the following ways:
(i) It groups identical values in the data together, so it is easy to observe and count them.
(ii) It shows you at a glance the lowest and highest values in the data set.
3. Are there other ways to arrange the data?
Answer:
You can arrange the data in descending order, by starting with the larger values first and ending with the smallest values. This is another way of grouping identical values first, making them easy to observe and count. It also easily shows you the lowest and highest values in the data set.
4. Write the names of a few trees you see around you. When you observe a tree on the way from your home to school (or while walking from one place to another place), record the data and fill in the following table—
| Tree | No. of Trees |
| Peepal | |
| Neem | |
| … | |
| … |
a. Which tree was found in the greatest number?
b. Which tree was found in the smallest number?
c. Were there any two trees found in the same numbers?
Answer:
Number of trees we observed on the way from your home to school are recorded as data and filled in the following table:
| Tree | No. of Trees |
| Peepal | 12 |
| Neem | 10 |
| Teek | 5 |
| Mango | 11 |
| Apple | 15 |
| Banana | 2 |
a. The tree found in greatest number was apple tree (15).
b. The tree found in the smallest number is banana tree (2).
c. No tree was found in the same numbers.
5. Take a blank piece of paper and paste any small news item from a newspaper. Each student may use a different article. Now, prepare a table on the piece of paper as given below. Count the number of each of the letters ‘c’, ‘e’, ‘i’, ‘r’, and ‘x’ in the words of the news article, and fill in the table.
| Letter | c | e | i | r | x | Any other letter of your choice: |
| Number of times found in the news item |
a. The letter found the most number of times is ________
b. The letter found the least number of times is ________
c. List the five letters ‘c’, ‘e’, ‘i’, ‘r’, ‘x’ in ascending order of frequency. Now, compare the order of your list with that of your classmates. Is your order the same or nearly the same as theirs? (Almost everyone is likely to get the order ‘x, c, r, i, e’.) Why do you think this is the case?
d. Write the process you followed to complete this task.
e. Discuss with your friends the processes they followed.
f. If you do this task with another news item, what process would you follow?
Answer:
We count the number of each of the letters c’, ‘e’, ‘i’, ‘r’, and ‘x’ in the words of the news article and fill in the table below:
| Letter | c | e | i | r | x | Any other letter of your choice (y) |
| Number of times found in the news item | 7 | 19 | 18 | 16 | 2 | 5 |
a. The letter found the most number of times is 19.
b. The letter found the least number of times is 2.
c. The five letters ‘c’, ‘e’, ‘i’, ‘r’, ‘x’ in ascending order of frequency are ‘x, c, r, i, e’. The reason is the following:
(i) ‘x’ is the least common letter, appearing in very few words.
(ii) ‘c’ occurs somewhat commonly, but still less frequent compared to vowels and more commonly used consonants.
(iii) ‘r’ is a frequently used consonant in English.
(iv) ‘I is a common vowel, present in numerous words.
(v) ‘e’ is the most common letter in the English language, appearing in countless words.
d. We follow the following process to complete this task:
(i) We take a blank piece of paper and paste a small news item from a local newspaper about a lost puppy who was rescued and brought to safety.
(ii) One by one, we take the letters ‘c’, ‘e’, ‘i’, ‘r’, ‘x’ and observe how many times they occur in the passage.
(iii) We then record our observations in the given table.
e. Some of our friends followed a similar process and others followed a slightly different process. One friend circled the letters ‘x, c, r, i, e’ one by one in different colours to make counting easier.
f. For another news item we would first highlight each letter first in different colours and then follow the same process of counting and tabulating.
In-text Questions (Page 82):
If they want to show their data through a pictograph, where they also use one symbol for each student, as Lakhanpal did, what are the challenges they might face?
Answer:
If Jarina and Sangita want to show their data through a pictograph, where they also use one symbol for each student, as Lakhanpal did, the challenges they might face include the following:
- Since there are a large number of students for each class, there will be many symbols and the pictograph will become overcrowded.
- The pictograph will be challenging to draw because there will be a large number of symbols.
- The pictograph will be challenging to read, as there will be a large number of symbols for every class.
In-text Questions (Page 83):
What could be the problems faced in preparing such a pictograph, if the total number of students present in a class is 33 or 27?
Answer:
If the total number of students present in a class is 33 or 27, the problems faced in preparing such a pictograph are as follows:
Representation: 33 or 27 are not exact multiples of 5 or 10, hence it would be difficult to represent the data using these scales. The symbols would need to be divided into fractions, which is not easy to achieve.
Reading: Since the symbols would need to be divided into fractions to maintain accuracy, the exact numerical values in the pictograph would be hard to decipher.
Figure it Out (Page 83):
1. The following pictograph shows the number of books borrowed by students, in a week, from the library of Middle School, Ginnori—
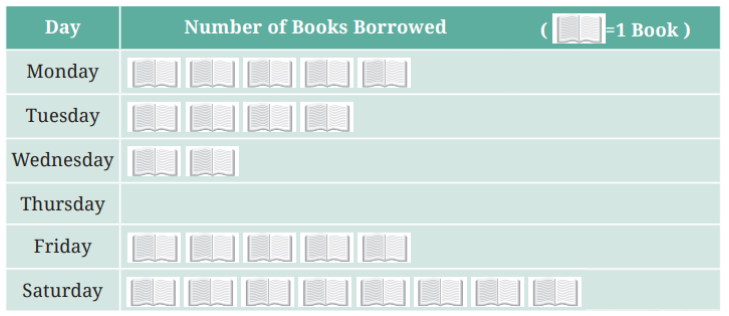
a. On which day were the minimum number of books borrowed?
b. What was the total number of books borrowed during the week?
c. On which day were the maximum number of books borrowed? What may be the possible reason?
Answer:
a. The minimum number of books (0 books) were borrowed on Thursday, as read from the pictograph.
b. The total number of books borrowed during the week = 5 + 4 + 2 + 0 + 5 + 8 = 24.
c. The maximum number of books were borrowed on Saturday (8 books). The possible reason is that Saturday is a holiday, hence students had more time to visit the library and borrow books.
2. Magan Bhai sells kites at Jamnagar. Six shopkeepers from nearby villages come to purchase kites from him. The number of kites he sold to these six shopkeepers are given below—
| Shopkeeper | Number of Kites sold |
| Chaman | 250 |
| Rani | 300 |
| Rukhsana | 100 |
| Jasmeet | 450 |
| Jetha Lal | 250 |
| Poonam Ben | 700 |
Prepare a pictograph using the symbol ![]() to represent 100 kites. Answer the following questions:
to represent 100 kites. Answer the following questions:
a. How many symbols represent the kites that Rani purchased?
b. Who purchased the maximum number of kites?
c. Who purchased more kites, Jasmeet or Chaman?
d. Rukhsana says Poonam Ben purchased more than double the number of kites that Rani purchased. Is she correct? Why?
Answer:
The pictograph is shown below:
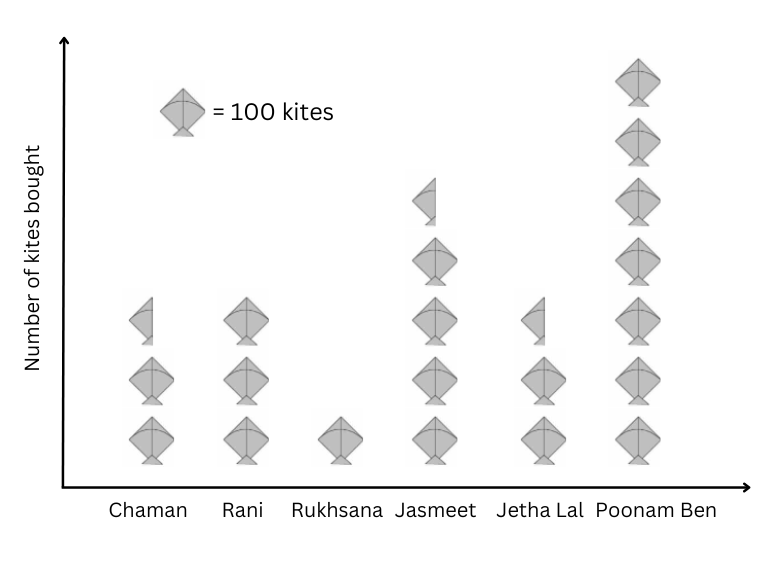
a. Rani purchased 300 kites.
1 symbol = 100 kites.
Therefore, the number of symbols that represent the kites that Rani purchased = 300/100 = 3.
b. Poonam Ben purchased the maximum number of kites with a total of 700 kites.
c. Jasmeet purchased 450 kites which was more than Chaman who purchased a total of 250 kites.
d. Poonam Ben purchased 700 kites and Rani purchased 300 kites.
We note: 700 = 300 × 2 + 100
Therefore, Rukhsana was right in saying that Poonam Ben purchased more than double the number of kites that Rani purchased.
In-text Questions (Page 86):
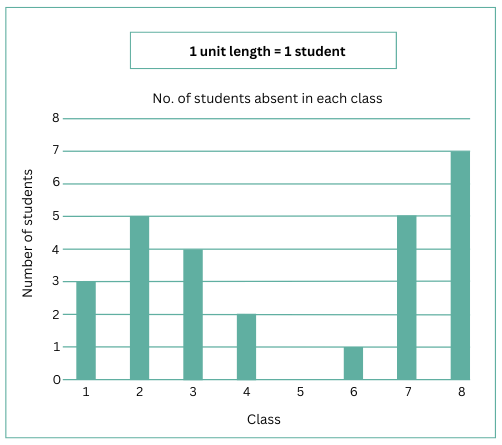
Answer the following questions using the bar graph:
1. In Class 2, ___________ students were absent that day.
2. In which class were the maximum number of students absent? ___________
3. Which class had full attendance that day? ___________
Answer:
1. In Class 2, 5 students were absent that day.
2. In which class were the maximum number of students absent? Class 8
3. Which class had full attendance that day? Class 5
Figure it Out (Page 88):
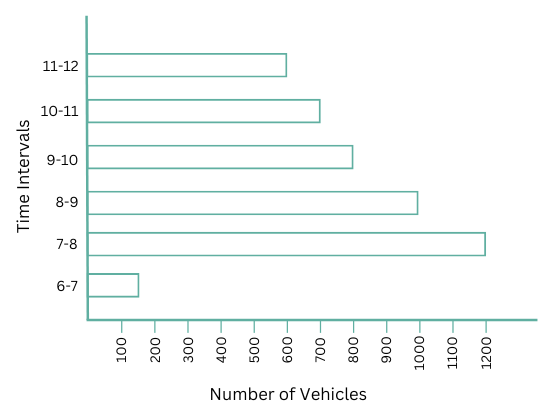
1. How many total cars passed through the crossing between 6 am and noon?
2. Why do you think so little traffic occurred during the hour of 6–7 am, as compared to the other hours from 7 am-noon?
3. Why do you think the traffic was the heaviest between 7 am and 8 am?
4. Why do you think the traffic was lesser and lesser each hour after 8am all the way until noon?
Answer:
1. Number of cars passed during each time interval is shown below:
| Time Interval | Number of Vehicles |
| 6-7 am | 150 |
| 7-8 am | 1200 |
| 8-9 am | 1000 |
| 9-10 am | 800 |
| 10-11 am | 700 |
| 11-12 am | 600 |
Total cars passed through the crossing between 6 am and noon = 150 + 1200 + 1000 + 800 + 700 + 600 = 4450.
2. So little traffic occurred during the hour of 6-7 am as compared to the other hours from 7 am-noon because it was early in the morning and people had not started their activities as of yet.
3. The traffic was the heaviest between 7 am and 8 am because it is during the morning rush hour. This is the time interval when most people drive to attend work, school and other duties.
4. The traffic likely became lighter each hour after 8 a.m. because the morning rush hour, when most people commute to work, school, or other destinations, peaks between 7 a.m. and 9 a.m. After 8 a.m., many commuters have already reached their destinations, resulting in fewer vehicles on the road. Additionally, mid-morning typically sees fewer scheduled activities compared to early morning, leading to a natural decline in traffic until it picks up again around lunchtime.
In-text Questions (Page 89):
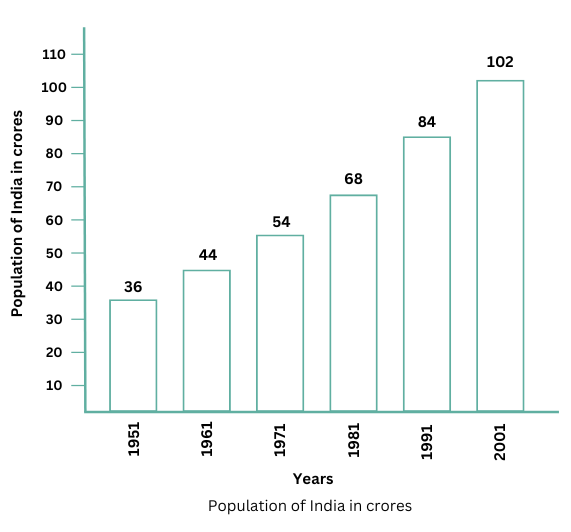
• On the basis of this bar graph, what may be a few questions you may ask your friends?
• How much did the population of India increase over 50 years? How much did the population increase in each decade?
Answer:
On the basis of this bar graph, a few questions you may ask your friends are as follows:
- In which decade was the increase in population maximum?
- Can you identify any year when the population did not increase?
- What was the population of India in 1981?
The increase in the population of India over 50 years = (102 – 36) = 66 crores.
The population increase in each decade can be represented by the table below:
| Decade | Increase in Population (in crores) |
| 1951-1961 | 44 – 36 = 8 |
| 1961-1971 | 54 – 44 = 10 |
| 1971-1981 | 68 – 54 = 14 |
| 1981-1991 | 84 – 68 = 16 |
| 1991-2001 | 102 – 84 = 18 |
In-text Questions (Page 92):
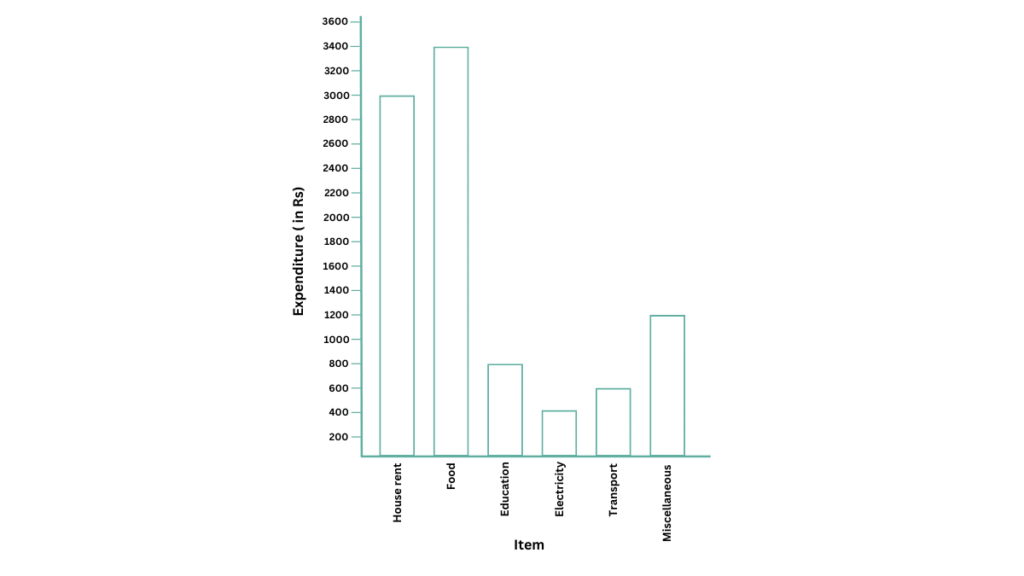
Use the bar graph to answer the following questions:
1. On which item does Imran’s family spend the most and the second most?
2. Is the cost of electricity about one-half the cost of education?
3. Is the cost of education less than one-fourth the cost of food?
Answer:
1. According to the bar graph, Imran’s family spends the most on food (as indicated by the highest bar) and the second most on house rent (as indicated by the second highest bar).
2. The cost of electricity = ₹ 400 and the cost of education = ₹ 800. Since 400/800 = 1/2, we conclude that the cost of electricity is one-half the cost of education.
3. Cost of education = ₹ 800 and cost of food = ₹ 3400. Since 3400 is more than four times 800, we conclude that the cost of education is less than one-fourth the cost of food.
Figure it Out (Page 93):
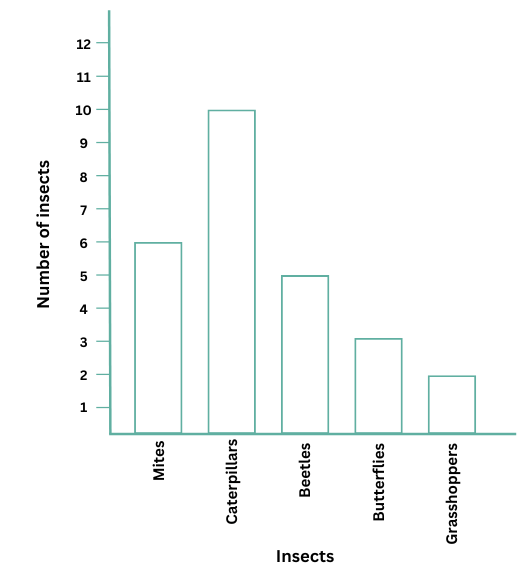
1. Samantha visited a tea garden and collected data of the insects and critters she saw there. Here is the data she collected—
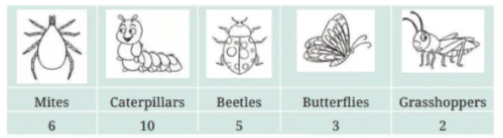
Help her prepare a bar graph representing this data.
Answer:
2. Pooja collected data on the number of tickets sold at the Bhopal railway station for a few different cities of Madhya Pradesh over a 2-hour period.
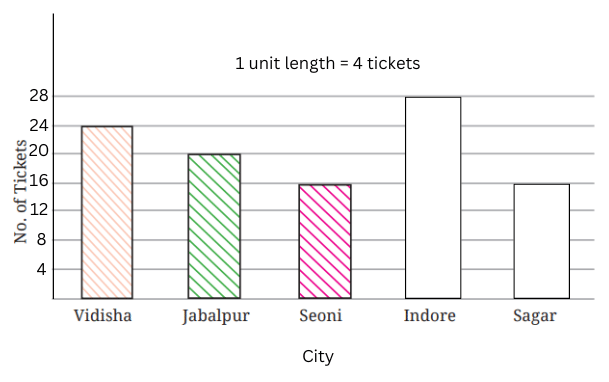
| City | Vidisha | Jabalpur | Seoni | Indore | Sagar |
| Number of tickets | 24 | 20 | 16 | 28 | 16 |
She used this data and prepared a bar graph on the board to discuss the data with her students, but someone erased a portion of the graph.
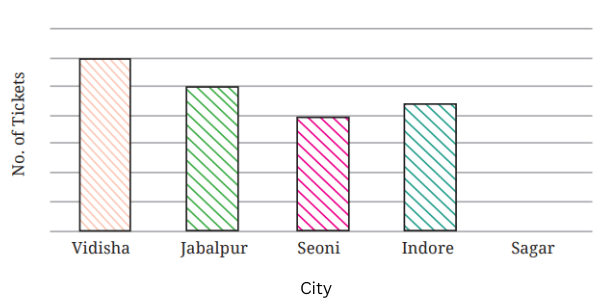
a. Write the number of tickets sold for Vidisha above the bar.
b. Write the number of tickets sold for Jabalpur above the bar.
c. The bar for Vidisha is 6 unit lengths and the bar for Jabalpur is 5 unit lengths. What is the scale for this graph?
d. Draw the correct bar for Sagar.
e. Add the scale of the bar graph placing the correct numbers on the vertical axis.
f. Are the bars for Seoni and Indore correct in this graph? If not, draw the correct bar(s).
Answer:
a. Write the number of tickets sold for Vidisha above the bar.
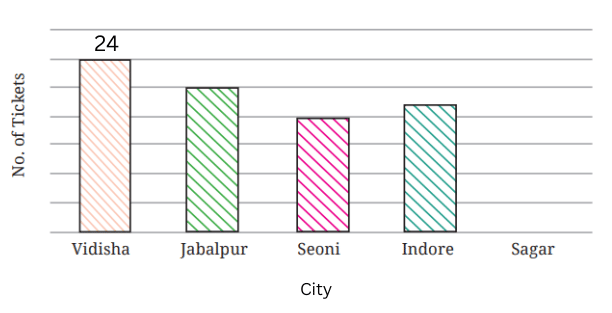
b. Write the number of tickets sold for Jabalpur above the bar.
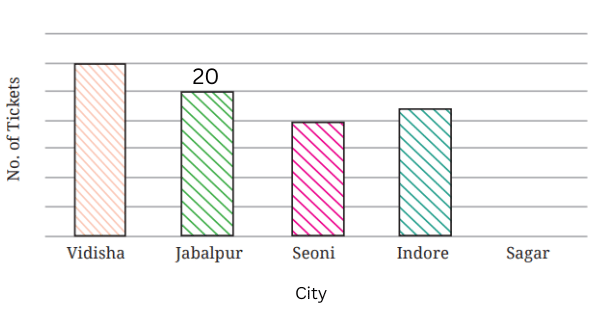
c. The bar for Vidisha is 6 unit lengths and the bar for Jabalpur is 5 unit lengths. What is the scale for this graph?
The bar for Vidisha is 6 unit lengths.
Number of tickets sold for Vidisha = 24.
Therefore, the scale is 1 unit length = 24/6 = 4 tickets.
The bar for Jabalpur is 5 unit lengths.
Number of tickets sold for Jabalpur = 20.
Therefore, we confirm that the scale is 1 unit length = 20/5 = 4 tickets.
d. Draw the correct bar for Sagar.
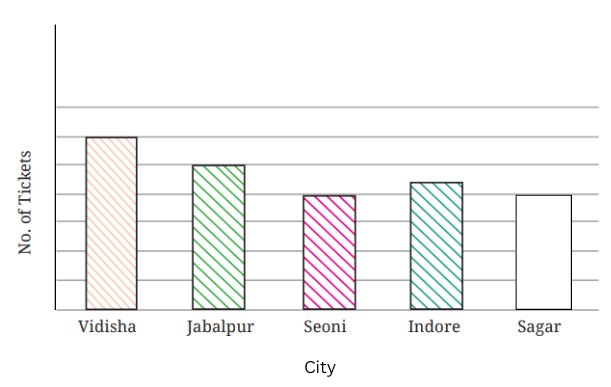
The correct bar for Sagar is above.
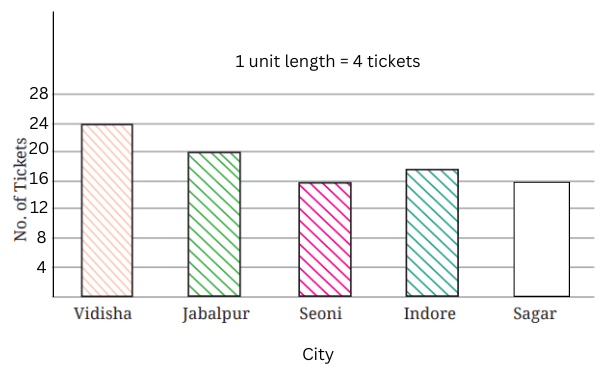
e. Add the scale of the bar graph placing the correct numbers on the vertical axis.
f. Are the bars for Seoni and Indore correct in this graph? If not, draw the correct bar(s).
3. Chinu listed the various means of transport that passed across the road in front of his house from 9 to 10 AM:

a. Prepare a frequency distribution table for the data.
b. Which means of transport was used the most?
c. If you were there to collect this data, how could you do it? Write the steps or process.
Answer:
a. Frequency distribution table is shown below:
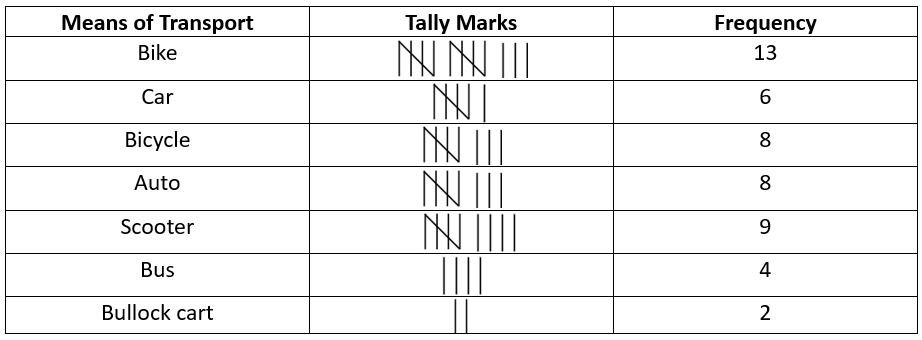
b. Bike was used as a means of transport the most.
c. If I were to collect this data I would follow the following process:
(i) Think about the various forms of transport in your locality and write down their names in a column.
(ii) Use tally marks to count the number of each vehicle that passes by and put them in a second column.
(iii) Counting the tally marks, write the frequency of each type of vehicle in a third column.
4. Roll a die 30 times and record the number you obtain each time. Prepare a frequency distribution table using tally marks. Find the number that appeared:
a. The minimum number of times.
b. The maximum number of times.
c. Find numbers that appeared an equal number of times.
Answer:
Rolling a die 30 times gives us the following outcomes:
1, 5, 4, 4, 2, 6, 4, 3, 1, 2, 3, 3, 4, 6, 6, 3, 1, 2, 3, 4, 5, 4, 6, 2, 3, 1, 1, 2, 5, 3.
The frequency distribution table is shown below:
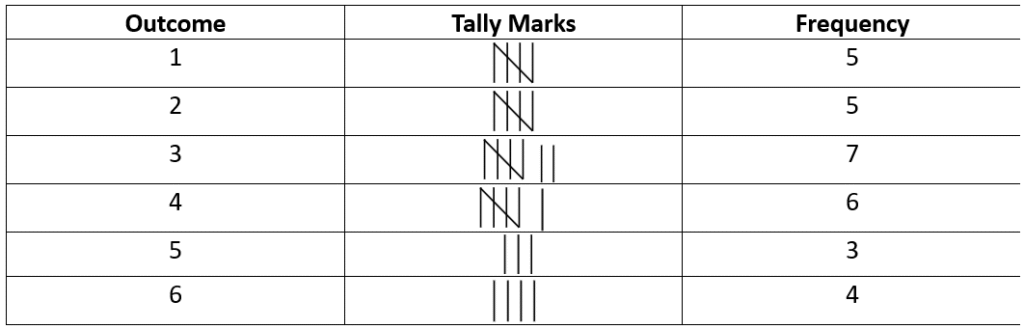
a. The number that appeared minimum number of times is 5 (only 3 times).
b. The number that appeared maximum number of times is 3 (7 times).
c. The numbers that appeared an equal number of times are 1 and 2 (both 5 times).
5. Faiz prepared a frequency distribution table of data on the number of wickets taken by Jaspreet Bumrah in his last 30 matches:
| Wickets Taken | Number of Matches |
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 3 |
| 5 | 5 |
| 6 | 1 |
| 7 | 1 |
a. What information is this table giving?
b. What may be the title of this table?
c. What caught your attention in this table?
d. In how many matches has Bumrah taken 4 wickets?
e. Mayank says “If we want to know the total number of wickets he has taken in his last 30 matches, we have to add the numbers 0, 1, 2, 3 …, up to 7.” Can Mayank get the total number of wickets taken in this way? Why?
f. How would you correctly figure out the total number of wickets taken by Bumrah in his last 30 matches, using this table?
Answer:
a. The number of wickets taken by Jaspreet Bumrah in his last 30 matches.
b. The title of this table can be “Wickets Taken by Jaspreet Bumrah in Last 30 Matches.”
c. The maximum number of wickets that Jasprit Bumrah took is 7.
d. Bumrah took 4 wickets in 3 matches.
e. No, Mayank cannot get the total number of wickets by adding the numbers 0, 1, 2, 3 …, up to 7. The reason is that he took each of these numbers of wickets in multiple matches. Hence, we have to multiply those numbers of wickets by the corresponding numbers of matches to get the total number of wickets taken.
f. We have to multiply the wickets by the corresponding numbers of matches to get the total number of wickets taken.
Total number of wickets taken = (0 × 2) + (1 × 4) + (2 × 6) + (3 × 8) + (4 × 3) + (5 × 5) + (6 × 1) + (7 × 1) = 0 + 4 + 12 + 24 + 12 + 25 + 6 + 7 = 90.
6. The following pictograph shows the number of tractors in five different villages.

Observe the pictograph and answer the following questions—
a. Which village has the smallest number of tractors?
b. Which village has the most tractors?
c. How many more tractors does Village C have than Village B?
d. Komal says, “Village D has half the number of tractors as Village E.” Is she right?
Answer:
a. Village D has the smallest number of tractors (3 tractors).
b. Village C has the most tractors (8 tractors).
c. Number of tractors in Village C = 8.
Number of tractors in Village B = 5.
Therefore, Village C has (8 – 5) = 3 tractors more than Village B.
d. Number of tractors in Village D = 3.
Number of tractors in Village E = 6.
Therefore, we conclude that Village D has half the number of tractors as Village E.
7. The number of girl students in each class of a school is depicted by a pictograph:

Observe this pictograph and answer the following questions:
a. Which class has the least number of girl students?
b. What is the difference between the number of girls in Class 5 and 6?
c. If 2 more girls were admitted in Class 2, how would the graph change?
d. How many girls are there in Class 7?
Answer:
a. Class 8 has the least number of girl students (4 + 2 = 6 students).
b. Number of girls in Class 5 = 4 + 4 + 2 = 10.
Number of girls in Class 6 = 4 + 4 + 4 + 4 = 16.
The difference between the number of girls in Class 5 and 6 = 16 – 10 = 6.
c. The number of girl students in Class 2 = 4 + 4 + 4 + 4 + 2 = 18
If 2 more girls were admitted in Class 2, the new number of girl students = 18 + 2 = 20.
The scale is ‘1 girl head’ = 4 girls.
Therefore, the number of girl heads for Class 2 = 20/5 = 5.
The required graph is shown below:

d. The number of girls in Class 7 = 4 + 4 + 4 = 12.
8. Mudhol Hounds (a type of breed of Indian dogs) are largely found in North Karnataka’s Bagalkote and Vijaypura districts. The government took an initiative to protect this breed by providing support to those who adopted these dogs. Due to this initiative, the number of these dogs increased. The number of Mudhol dogs in six villages of Karnataka are as follows—
Village A : 18, Village B : 36, Village C : 12, Village D : 48, Village E : 18, Village F : 24
Prepare a pictograph and answer the following questions:
a. What will be a useful scale or key to draw this pictograph?
b. How many symbols will you use to represent the dogs in Village B?
c. Kamini said that the number of dogs in Village B and Village D together will be more than the number of dogs in the other 4 villages. Is she right? Give reasons for your response.
Answer:
The required pictograph is shown below:

a. ‘1 symbol = 12 hounds’ is a useful scale or key to draw this pictograph.
b. We use 3 symbols to represent the dogs in Village B.
c. The number of dogs in Village B and Village D together = 36 + 48 = 84.
The number of dogs in the other 4 villages = 18 + 12 + 18 + 24 = 72.
Therefore, we can see that the number of dogs in Village B and Village D together will be more than the number of dogs in the other 4 villages.
9. A survey of 120 school students was conducted to find out which activity they preferred to do in their free time.
| Preferred Activity | Number of Students |
| Playing | 45 |
| Reading story books | 30 |
| Watching TV | 20 |
| Listening to music | 10 |
| Painting | 15 |
Draw a bar graph to illustrate the above data taking the scale of 1 unit length = 5 students. Which activity is preferred by most students other than playing?
Answer:
The bar graph to illustrate the above data taking the scale of 1 unit length = 5 students is shown below:
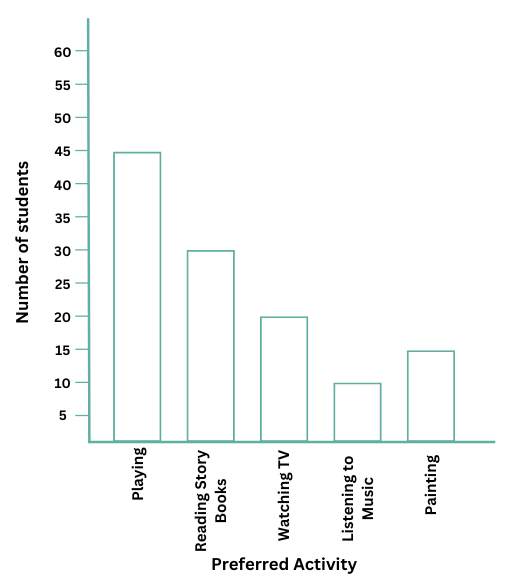
The activity which is preferred by most students other than playing is ‘reading story books’, as indicated by the second highest bar in the bar graph.
10. Students and teachers of a primary school decided to plant tree saplings in the school campus and in the surrounding village during the first week of July. Details of the saplings they planted are as follows—
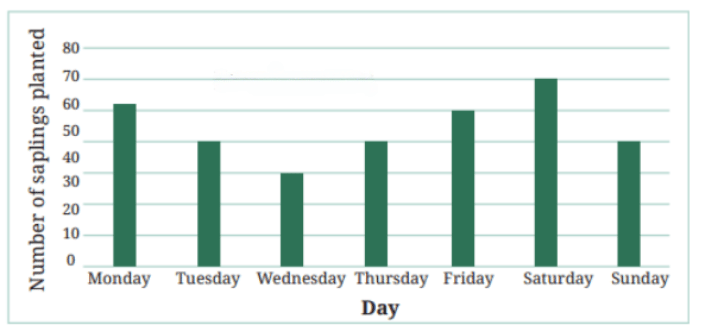
a. The total number of saplings planted on Wednesday and Thursday is ___________.
b. The total number of saplings planted during the whole week is ___________.
c. The greatest number of saplings were planted on ___________, and the least number of saplings were planted on ___________. Why do you think that is the case? Why were more saplings planted on certain days of the week and less on others? Can you think of possible explanations or reasons? How could you try and figure out whether your explanations are correct?
Answer:
a. The total number of saplings planted on Wednesday and Thursday is 70 (30 + 40).
b. The total number of saplings planted during the whole week is 312 (52 + 40 + 30 + 40 + 50 + 60 + 40).
c. The greatest number of saplings were planted on Saturday, and the least number of saplings were planted on Wednesday.
Students and teachers planted a large number of saplings on Monday because they were energetic after resting during the weekend.
They planted lesser number of saplings mid-week due to exhaustion.
Towards the end of the week on Thursday and Friday, their activities increased again, possibly because they were anticipating the upcoming weekend.
Saturday is a holiday and so the largest number of saplings were planted on this day.
On Sunday they faced exhaustion after the sapling-planting activities on Saturday and were also busy preparing for the upcoming week. Hence, less saplings were planted on Sunday.
11. The number of tigers in India went down drastically between 1900 and 1970. Project Tiger was launched in 1973 to track and protect tigers in India. Starting in 2006, the exact number of tigers in India was tracked. Shagufta and Divya looked up information about the number of tigers in India between 2006 and 2022 in 4-year intervals. They prepared a frequency table for this data and a bar graph to present this data, but there are a few mistakes in the graph. Can you find those mistakes and fix them?

Answer:
The mistakes in the graph can be fixed as follows:
- The bar for year 2006 is less than the 1000 mark, whereas it should be around middle of the second and third units.
- The bar for 2010 is too short and be closer to the 2000 mark.
- The bar for 2014 should be reduced to a little above the 2000 mark.
- The bar for 2018 should be extended upto the 3000 mark.
The correct bar graph is shown below:
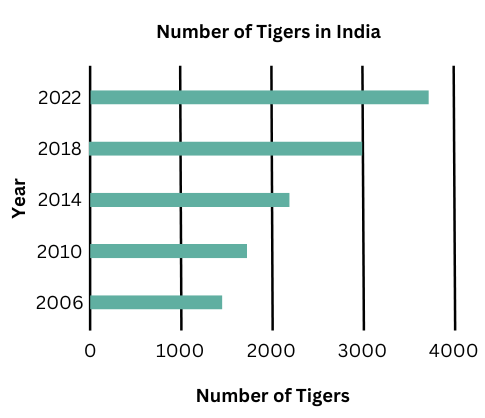
Figure it Out (Page 103):
1. If you wanted to visually represent the data of the heights of the tallest persons in each class in your school, would you use a graph with vertical bars or horizontal bars? Why?
Answer:
A graph of vertical bars is suitable to visually represent the data of the heights of the tallest persons in each class in your school.
The reason it that it is more intuitive, suggestive, and visually appealing to represent heights, that are measured upwards from the ground, using bar graphs that have vertical bars or columns.
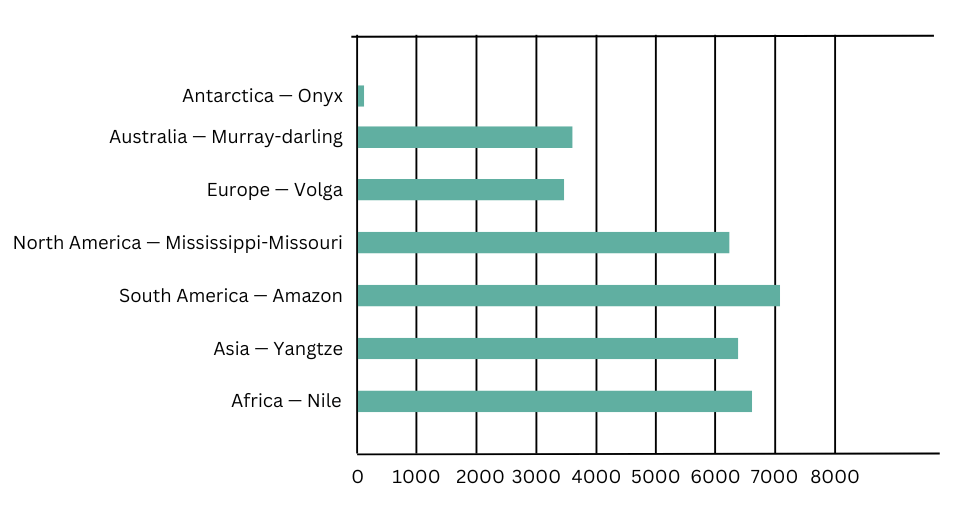
2. If you were making a table of the longest rivers on each continent and their lengths, would you prefer to use a bar graph with vertical bars or with horizontal bars? Why? Try finding out this information, and then make the corresponding table and bar graph! Which continents have the longest rivers?
Answer:
A graph of horizontal bars is suitable for making a table of the longest rivers on each continent and their lengths.
The reason is that the lengths that are parallel to the ground (e.g., rivers running across the face of the Earth) are usually best represented using bar graphs with horizontal bars.
Here’s the table of the longest rivers by continent:
| Continent | River | Length (km) |
| Africa | Nile | 6,650 |
| Asia | Yangtze | 6,300 |
| South America | Amazon | 7,062 |
| North America | Mississippi-Missouri | 6,275 |
| Europe | Volga | 3,350 |
| Australia | Murray-Darling | 3,672 |
| Antarctica | Onyx | 40 |
The corresponding bar graph is shown below: