Figure it Out (Page 132):
1. Find the missing terms:
a. Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?.
b. Perimeter of a square = 20 cm; side of a length = ?.
c. Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?.
Answer:
a. Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?.
Perimeter = 2 × (length + breadth)
14 = 2 × (length + 2)
(length + 2) = 14/2
length + 2 = 7
length = 7 – 2
length = 5 cm
b. Perimeter of a square = 20 cm; side of a length = ?.
Perimeter of a square = 4 × length of a side
20 = 4 × length of a side
length of a side = 20/4
length of a side = 5 cm
c. Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?.
Perimeter = 2 × (length + breadth)
12 = 2 × (3 + breadth)
(3 + breadth) = 12/2
3 + breadth = 6
breadth = 6 – 3
breadth = 3 cm
2. A rectangle having side lengths 5 cm and 3 cm is made using a piece of wire. If the wire is straightened and then bent to form a square, what will be the length of a side of the square?
Answer:
Perimeter of rectangle = 2 × (length + breadth)
Perimeter of rectangle = 2 × (5 + 3)
Perimeter of rectangle = 16 cm
The same wire is straightened and then bent to form a square.
Therefore, perimeter of square = Perimeter of rectangle
4 × length of a side of square = 16
Length of a side of square = 16/4
Length of a side of square = 4 cm
3. Find the length of the third side of a triangle having a perimeter of 55 cm and having two sides of length 20 cm and 14 cm, respectively.
Answer:
Perimeter of triangle = 55 cm
Therefore,
Sum of sides = 55
20 + 14 + (third side) = 55
34 + (third side) = 55
Third side = 55 – 34
Third side = 21 cm
4. What would be the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m, if the fence costs ₹ 40 per metre?
Answer:
Perimeter of rectangular park = 2 × (length + breadth)
Perimeter of rectangular park = 2 × (150 + 120) = 540 metre.
The fence costs ₹ 40 per metre.
Therefore, the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m = (540 metre × ₹ 40 per metre) = ₹ 21,600.
5. A piece of string is 36 cm long. What will be the length of each side, if it is used to form:
a. A square,
b. A triangle with all sides of equal length, and
c. A hexagon (a six sided closed figure) with sides of equal length?
Answer:
a. A square
The piece of string 36 cm long is used to form a square.
Perimeter of a square = 4 × length of a side
4 × length of a side = 36
length of a side = 36/4 = 9 cm
b. A triangle with all sides of equal length, and
Perimeter of triangle = sum of three sides
All sides are of equal length.
Therefore,
3 × (length of each side) = 36
length of each side = 36/3 = 12 cm
c. A hexagon (a six sided closed figure) with sides of equal length?
Perimeter = Sum of six sides
All sides are of equal length.
Therefore,
6 × (length of each side) = 36
length of each side = 36/6 = 6 cm
6. A farmer has a rectangular field having length 230 m and breadth 160 m. He wants to fence it with 3 rounds of rope as shown. What is the total length of rope needed?
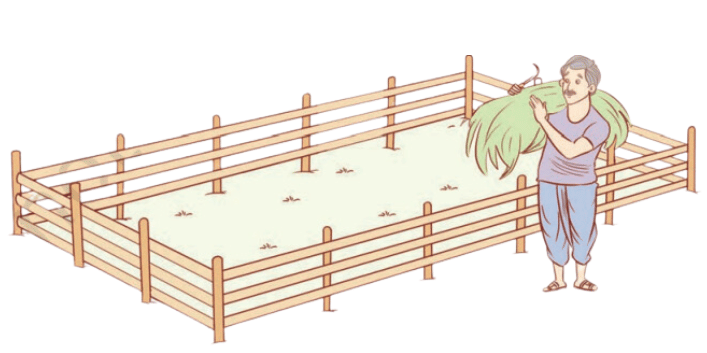
Answer:
Perimeter of rectangular field = 2 × (length + breadth)
Perimeter of rectangular field = 2 × (230 + 160) = 780 m.
The farmer wants to fence the rectangular field with 3 rounds of rope.
Therefore, the total length of rope needed = 780 × 3 = 2340 m.
Page 133:
Matha Pachchi!
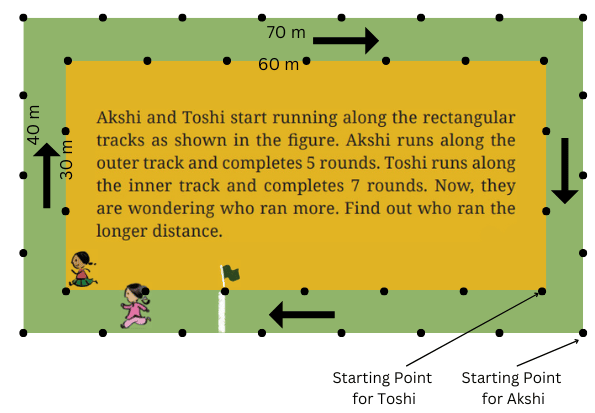
Each track is a rectangle. Akshi’s track has length 70 m and breadth 40 m. Running one complete round on this track would cover 220 m, i.e., 2 × (70 + 40) m = 220 m. This is the distance covered by Akshi in one round.
Figure it Out (Page 133):
1. Find out the total distance Akshi has covered in 5 rounds.
Answer:
Akshi’s rectangular track has length 70 m and breadth 40 m.
Distance Akshi has covered in 1 round = perimeter of rectangle = 2 × (length + breadth) = 2 × (70 + 40) m = 220 m.
Therefore, the total distance Akshi has covered in 5 rounds = (5 × 220) m = 1100 m.
2. Find out the total distance Toshi has covered in 7 rounds. Who ran a longer distance?
Answer:
Toshi rectangular track has length 60 m and breadth 30 m.
Distance Toshi has covered in 1 round = perimeter of rectangle = 2 × (length + breadth) = 2 × (60 + 30) = 180 m.
Therefore, the total distance Toshi has covered in 7 rounds = (7 × 180) m = 1260 m.
Therefore, Toshi covered in 7 rounds more distance by (1260 – 1100) m = 160 m than Akshi covered in 5 rounds.
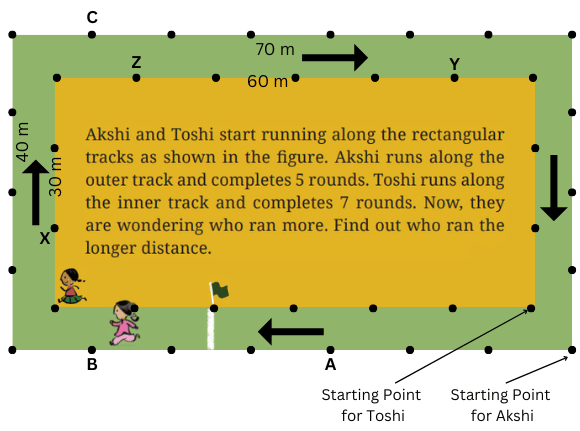
3. Think and mark the positions as directed—
a. Mark ‘A’ at the point where Akshi will be after she ran 250 m.
b. Mark ‘B’ at the point where Akshi will be after she ran 500 m.
c. Now, Akshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘C’.
d. Mark ‘X’ at the point where Toshi will be after she ran 250 m.
e. Mark ‘Y’ at the point where Toshi will be after she ran 500 m.
f. Now, Toshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘Z’.
Answer:
a. Mark ‘A’ at the point where Akshi will be after she ran 250 m.
For Akshi length of total track = (70 + 40 + 70 + 40) m = 220 m.
Akshi’s track is divided into 22 divisions.
Therefore, distance between any two divisions = (220 ÷ 22) m = 10 m.
Distance Akshi has run = 250 m.
Extra distance Akshi has run beyond one round = (250 – 220) m = 30 m.
Number of divisions Akshi has covered after completing one round = (30 ÷ 10) = 3.
The point where Akshi will be after she ran 250 m is marked as ‘A’.
b. Mark ‘B’ at the point where Akshi will be after she ran 500 m.
Distance Akshi has run = 500 m.
Extra distance Akshi has run beyond one round = (500 – 2 × 220) = 60 m.
Number of divisions Akshi has covered after completing one round = (60 ÷ 10) = 6.
The point where Akshi will be after she ran 500 m is marked as ‘B’.
c. Now, Akshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘C’.
Distance Akshi has run = 1000 m.
We observe (4 × 220 m) = 880 m, which is less than 1000 m and (5 × 220 m) = 1100 m, which is more than 1000 m.
Therefore, Akshi has finished running around her track 4 complete times.
The extra distance covered after 4 rounds = (1000 m – 880 m) = 120 m
Number of divisions Akshi has covered after completing four rounds = (120 ÷ 10) = 12.
The point where Akshi will be after she ran 1000 m is marked as ‘C’.
d. Mark ‘X’ at the point where Toshi will be after she ran 250 m.
For Toshi length of total track = (60 + 30 + 60 + 30) m = 180 m.
Toshi’s track is divided into 18 divisions.
Therefore, distance between any two divisions = (180 ÷ 18) m = 10 m.
The extra distance covered after 250 m = (250 – 180) m = 70 m.
Number of extra divisions Toshi has covered = (70 ÷ 10) = 7.
The point where Toshi will be after she ran 250 m is marked as ‘X’.
e. Mark ‘Y’ at the point where Toshi will be after she ran 500 m.
After 2 rounds Toshi covered (180 × 2) = 360 m.
Therefore, after 2 rounds Toshi covered (500 – 360) m = 140 m.
Number of extra divisions Toshi has covered = (140 ÷ 10) = 14.
The point where Toshi will be after she ran 500 m is marked as ‘Y’.
f. Now, Toshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘Z’.
We observe that, (180 × 5) = 900 m which is < 1000 m, and (180 × 6) = 1080 m which is > 1000 m.
Therefore, she has finished running around her track 5 full times.
Extra distance covered after 5 rounds = 1000 m.
Number of extra divisions Toshi has covered = (100 ÷ 10) = 10.
The point where Toshi will be after she ran 1000 m is marked as ‘Z’.
In-text Questions (Page 134):
Deep Dive: In races, usually there is a common finish line for all the runners. Here are two square running tracks with the inner track of 100 m each side and outer track of 150 m each side. The common finishing line for both runners is shown by the flags in the figure which are in the center of one of the sides of the tracks.
If the total race is of 350 m, then we have to find out where the starting positions of the two runners should be on these two tracks so that they both have a common finishing line after they run for 350 m. Mark the starting points of the runner on the inner track as ‘A’ and the runner on the outer track as ‘B’.
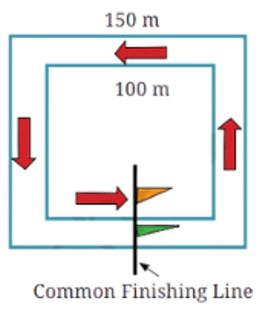
Answer:
The starting points of the runner on the inner track as ‘A’ and the runner on the outer track as ‘B’ are shown below:
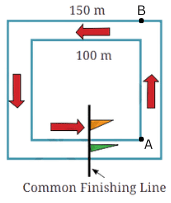
Starting from A, the distance covered till the runner reaches the finish line = (100 + 100 + 100 + 50) m = 350 m.
Now, the width of the path = (150 – 100)/2 = 50/2 = 25 m.
Therefore, starting from B, the distance covered till the runner reaches the finish line = (100 + 25 + 150 + 75) m = 350 m.
Estimate and Verify (Page 134):
Take a rough sheet of paper or a sheet of newspaper. Make a few random shapes by cutting the paper in different ways. Estimate the total length of the boundaries of each shape then use a scale or measuring tape to measure and verify the perimeter for each shape.
Answer:
Some sample newspaper cuttings are shown below:

Steps to follow:
1. Estimate the total length of the boundaries of each shape using the naked eye.
2. Then use a ruler to measure the length of each side.
3. Add up the lengths of all the sides to get the perimeter of the shape.
4. Compare the estimation with the actual perimeter of each shape.
Page 134:
Akshi says that the perimeter of this triangle shape is 9 units. Toshi says it can’t be 9 units and the perimeter will be more than 9 units. What do you think?
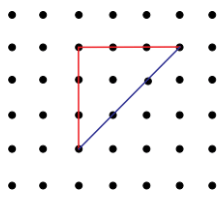
Answer:
Toshi is right when she says the perimeter will be more than 9 units.
The diagonal lines are longer than the horizontal and vertical lines.
Therefore,
Perimeter = (3 units) + (3 units) + (more than 3 units) = more than 9 units.
Page 135:
Write the perimeters of the figures below in terms of straight and diagonal units.
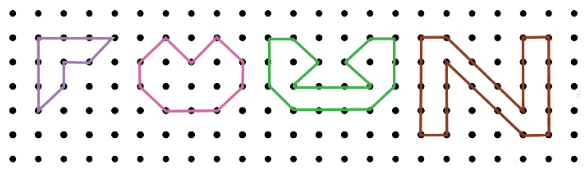
Answer:
Perimeter of Figure 1 = 8s + 2d
Perimeter of Figure 2 = 4s + 6d
Perimeter of Figure 3 = 12s + 6d
Perimeter of Figure 4 = 18s + 6d
Page 136:
Find various objects from your surroundings that have regular shapes and find their perimeters. Also, generalise your understanding for the perimeter of other regular polygons.
Answer:
The various objects from my surroundings that have regular shapes are given below along with their perimeters:
Square Tile:
Length of each side = 20 cm
Perimeter = 4 × (Length of each side) = 4 × 20 = 80 cm.
Triangular Traffic Signboards:
Length of each side = 40 cm
Perimeter = 3 × (Length of each side) = 3 × 40 = 120 cm.
Hexagonal Nuts & Bolts:
Length of each side: 5 mm
Perimeter = 6 × (Length of each side) = 6 × 5 = 30 mm.
Therefore, we generalise the formula for the perimeter of other regular polygons as:
Perimeter = n × (Length of each side), where n is the number of sides of the regular polygon.
Page 136:
Find out the length of the boundary (i.e., the perimeter) of each of the other arrangements below.
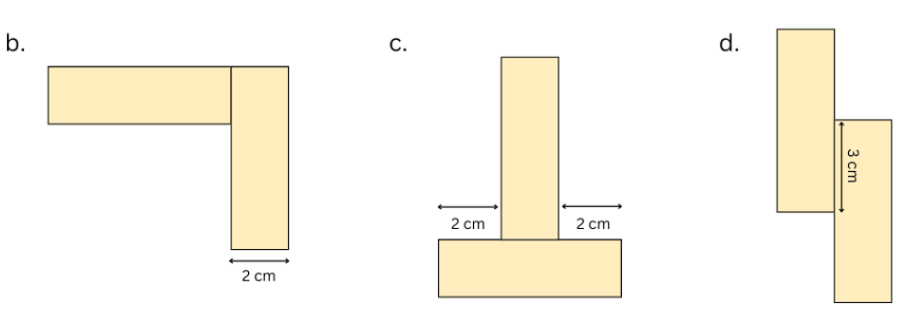
Answer:
b. Length of the boundary (i.e. perimeter) = 6 cm + 2 cm + 6 cm + 4 cm + 2 cm + 6 cm + 2 cm = 28 cm.
c. Length of the boundary (i.e. perimeter) = 2 cm + 6 cm + 2 cm + 2 cm + 6 cm + 2 cm + 2 cm + 6 cm = 28 cm.
d. Length of the boundary (i.e. perimeter) = 2 cm + 6 cm + 2 cm + 3 cm + 2 cm + 6 cm + 2 cm + 3 cm = 26 cm.
Page 136:
Arrange the two pieces to form a figure with a perimeter of 22 cm.
Answer:
The two pieces are arranged to form a figure with a perimeter of 22 cm as shown below:
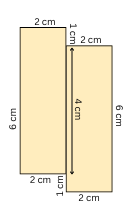
Perimeter = 2 cm + 6 cm + 2 cm + 1 cm + 2 cm + 6 cm + 2 cm + 1 cm = 22 cm.
Figure it Out (Page 138):
1. The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?
Answer:
Length of rectangular garden = 25 m.
Area of rectangular garden = Length × width = 300 sq m.
25 × width = 300
Breadth = 300/25 = 12 m.
Therefore, width of the garden = 12 m.
2. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m?
Answer:
Length of rectangular plot = 500 m.
Width of rectangular plot = 200 m.
Area of rectangular plot = Length × width = 500 m × 200 m = 100,000 sq m.
For 100 sq m the cost of tiling is ₹ 8.
For 1 sq m the cost of tiling is ₹ 8/100.
For 100,000 sq m the cost of tiling is (₹ 8/100) × 100,000 = ₹ 8000.
3. A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?
Answer:
Length of rectangular coconut grove = 100 m.
Width of rectangular coconut grove = 50 m.
Area of grove = Length × width = 100 × 50 = 5000 sq m.
Area occupied by each coconut tree = 25 sq m.
The maximum number of trees that can be planted in this grove = 5000/25 = 200 trees.
4. By splitting the following figures into rectangles, find their areas (all measures are given in metres):
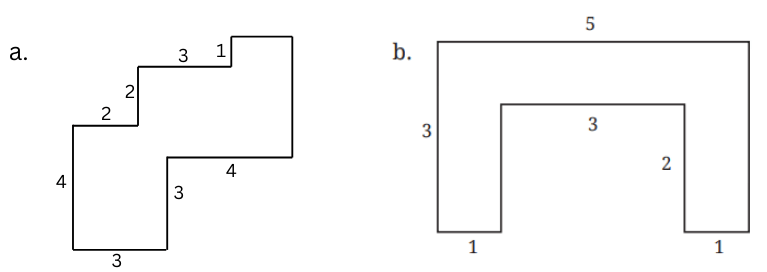
Answer:
a. Figure (a) can be split into rectangles as shown below:
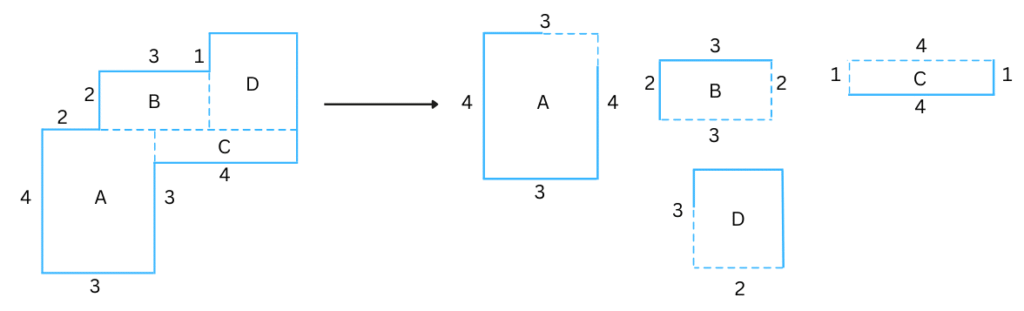
Area of A = 3 × 4 = 12 sq. m
Area of B = 3 × 2 = 6 sq. m
Area of C = 4 × 1 = 4 sq. m
Area of D = 2 × 3 = 6 sq. m
Area of Figure (a) = Area of A + Area of B + Area of C + Area of D = 12 + 6 + 4 + 6 = 28 sq. m.
b. Figure (b) can be split into rectangles as shown below:

Area of A = 1 × 3 = 3 sq. m.
Area of B = 3 × 1 = 3 sq. m.
Area of C = 1 × 3 = 3 sq. m.
Area of Figure (b) = Area of A + Area of B + Area of C = 3 + 3 + 3 = 9 sq. m.
Figure it Out (Page 139):
Cut out the tangram pieces given at the end of your textbook.
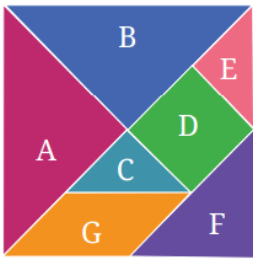
1. Explore and figure out how many pieces have the same area.
Answer:
A and B have the same area.
C and E have the same area.
2. How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D and E?
Answer:
Shape D is two times bigger than Shape C.
The relationship between Shapes C, D and E is as follows:
Area of C = ½ (Area of D) = Area of E
3. Which shape has more area: Shape D or F? Give reasons for your answer.
Answer:
Shapes D and F have the same area.
Reason: If Shape F is split into two equal triangles through the middle, they can be superimposed exactly on Shape D.
4. Which shape has more area: Shape F or G? Give reasons for your answer.
Answer:
Shapes F and G have the same area.
Reason: Draw a line from top left corner of G to bottom right corner of G, you get two triangles which can be superimposed exactly on F.
5. What is the area of Shape A as compared to Shape G? Is it twice as big? Four times as big?
Answer:
The area of Shape A is 2 times as big as Shape G.
Reason: Shape G can be divided into two equal triangles of a certain size. Shape A can be divided into four equal triangles of the same size. Hence, area of Shape A is 2 times as big as Shape G.
6. Can you now figure out the area of the big square formed with all seven pieces in terms of the area of Shape C?
Answer:
We get,
A = B = 4C
G = F = D = 2C
E = C
Area of the big square = (Area of A) + (Area of B) + (Area of G) + (Area of F) + (Area of D) + (Area of E) + (Area of C) = 4C + 4C + 2C + 2C + 2C + C + C = 16C.
7. Arrange these 7 pieces to form a rectangle. What will be the area of this rectangle in terms of the area of Shape C now? Give reasons for your answer.
Answer:
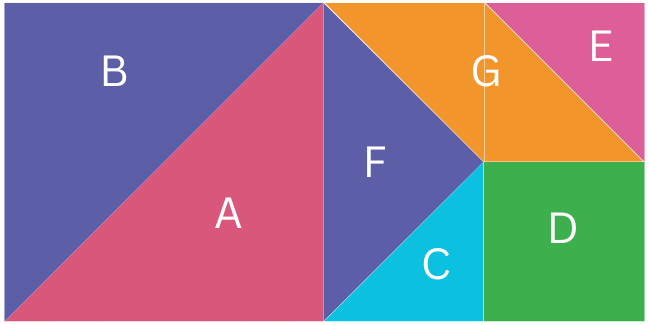
The area of this rectangle in terms of Shape C = 16C.
Reason: The rectangle is comprised of the same pieces as the square, hence area will be the same.
8. Are the perimeters of the square and the rectangle formed from these 7 pieces different or the same? Give an explanation for your answer.
Answer:
The perimeters of the square and the rectangle formed from these 7 pieces are different.
Reason: The shapes are arranged differently, hence the outer boundary or perimeter of the rectangle is different from the square.
Figure it Out (Page 140):
Look at the figures below and guess which one of them has a larger area.
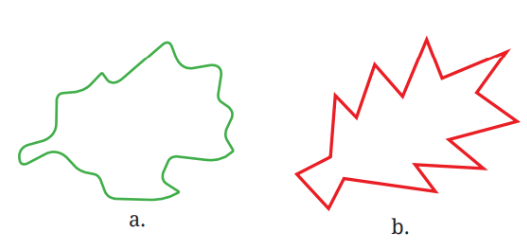
Answer:
It is difficult to guess which figure has a larger area just by looking at the figures because they are of similar size.
Figure it Out (Page 140):
Find the area of the following figures.

Answer:
To estimate the area, we can trace the shape onto a piece of transparent paper and place the same on a piece of squared or graph paper and then follow the below conventions—
1. The area of one full small square of the squared or graph paper is taken as 1 sq unit.
2. Ignore portions of the area that are less than half a square.
3. If more than half of a square is in a region, just count it as 1 sq unit.
4. If exactly half the square is counted, take its area as 1 2 sq unit.
From left to right:
Figure 1: Area =½ + 1 + 1 + 1 + ½ = 4 sq units.
Figure 2: Area = ½ + ½ + ½ + ½ + 1 + 1 + 1 + 1 + ½ + ½ + 1 + 1 = 9 sq units.
Figure 3: Area =1 + ½ + 1 + ½ + ½ + 1 + 1 + 1 + ½ + 1 + ½ + ½ + 1 = 10 sq units.
Figure 4: Area = 1 + 1 + 1 + 1 + ½ + ½ + ½ + ½ + ½ + ½ + 1 + 1 + 1 + 1 = 11 sq units.
Figure it Out (Page 141):
Try using different shapes (triangle and rectangle) to fill the given space (without overlaps and gaps) and find out the merits associated with using a square shape to find the area rather than another shape. List out the points that make a square the best shape to use to measure area.
1. Find the area (in square metres) of the floor outside of the corridor.
2. Find the area (in square metres) occupied by your school playground.
Answer:
We use different shapes: triangle, rectangle and squares to fill the given space as shown below:
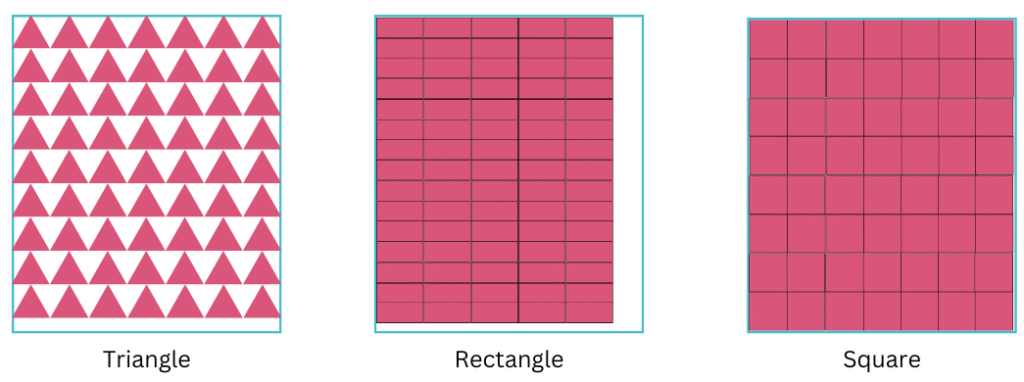
Merits associated with using a square shape to find the area rather than another shape are as follows:
(i) No Gaps or Overlaps – Squares tile perfectly, unlike triangles and rectangles.
(ii) Easy Area Calculation – Simple formula: Area = side × side.
Figure it Out (Page 141):
On a squared grid paper (1 square = 1 square unit), make as many rectangles as you can whose lengths and widths are a whole number of units such that the area of the rectangle is 24 square units.
a. Which rectangle has the greatest perimeter?
b. Which rectangle has the least perimeter?
c. If you take a rectangle of area 32 sq cm, what will your answers be? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter as well as the least perimeter? Give examples and reasons for your answer.
Answer: The required rectangles with area 24 square units are shown below:
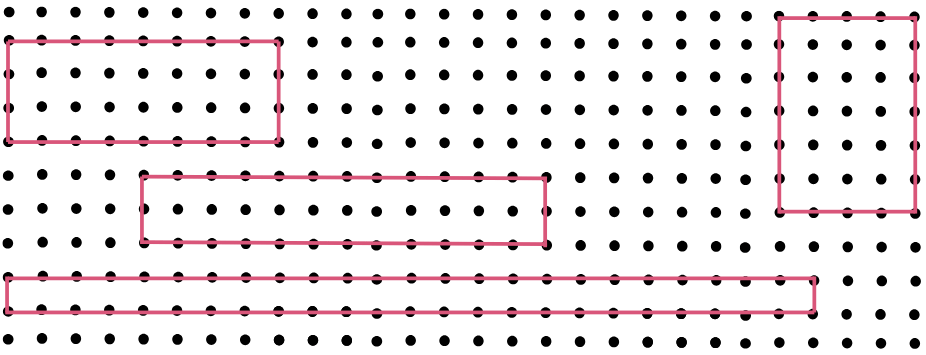
- The rectangle with the greatest perimeter is the one on the bottom (24 + 24 + 1 + 1 = 50 units).
- The rectangle with the least perimeter is the one on the top right (6 + 6 + 4 + 4 = 20 units).
- The rectangles of area 32 sq cm are shown below:
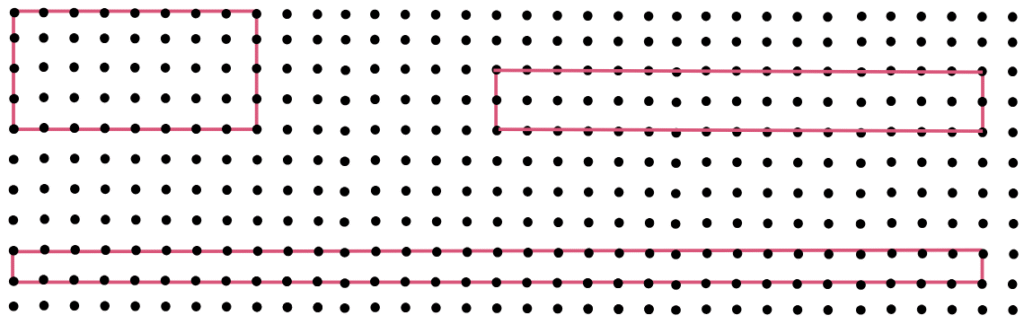
The rectangle with the greatest perimeter is the one on the bottom (32 + 32 + 1 + 1 = 66 units).
The rectangle with the least perimeter is the one on the top left (8 + 8 + 4 + 4 = 24 units).
Given any area, perimeter of the rectangle increases as the width decreases and the perimeter of the rectangle decreases as the width increases.
Figure it Out (Page 142):
Draw a rectangle on a piece of paper and draw one of its diagonals. Cut the rectangle along that diagonal and get two triangles.
Check! whether the two triangles overlap each other exactly. Do they have the same area?
Try this with more rectangles having different dimensions. You can check this for a square as well.
Can you draw any inferences from this exercise? Please write it here. ____________________________________________________________________________________________________________________________________________________________________
Answer:
The rectangle and one of its diagonals are drawn. The rectangle is cut along that diagonal to get two triangles as shown below:
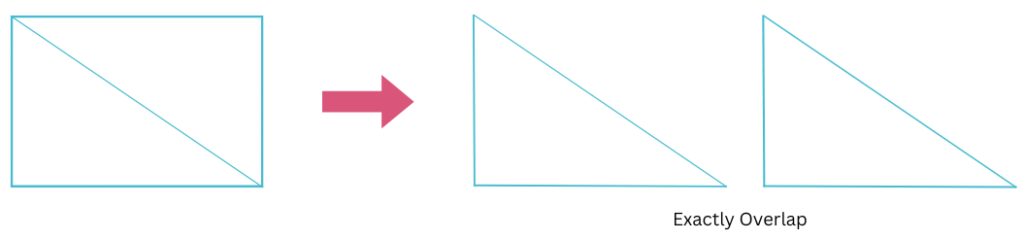
The triangles overlap each other exactly and have the same area.
Any rectangle will yield the same result.
Any square will yield the same result.
Inferences: A diagonal of a rectangle and a square always divides them into two triangles of equal area.
Figure it Out (Page 142):
Now, see the figures below. Is the area of the blue rectangle more or less than the area of the yellow triangle? Or is it the same? Why?

Can you see some relationship between the blue rectangle and the yellow triangle and their areas? Write the relationship here.
Answer:
The area of the blue rectangle = area of the yellow triangle.
Reason: The diagonal of the rectangle divides it into two triangles and the altitude of the yellow triangle divides it into two more triangles. The four triangles are all equal in area.
Figure it Out (Page 143):
Use your understanding from previous grades to calculate the area of any closed figure using grid paper and—
1. Find the area of blue triangle BAD. __________
2. Find the area of red triangle ABE. ___________
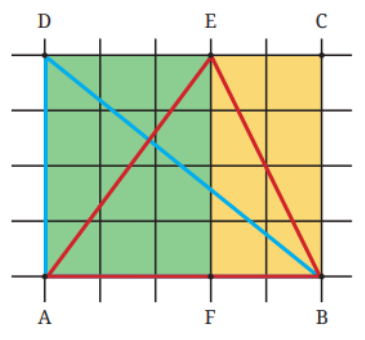
Area of rectangle ABCD = ________________
So, the area of triangle BAD is half of the area of the rectangle ABCD.
Conclusion ____________________________________________________ ______________________________________________________________
Answer:
1. Area of blue triangle BAD = (1/2) × base × height = (1/2) × 4 × 5 = 10 sq units.
2. Area of red triangle ABE = (1/2) × base × height = (1/2) × 4 × 5 = 10 sq units.
Area of rectangle ABCD = Length × Breadth = 5 × 4 = 20 sq units.
Conclusion: The area of any triangle with the same base and height as a rectangle will be equal to half the area of the rectangle.
Figure it Out (Page 144):
1. Find the areas of the figures below by dividing them into rectangles and triangles.
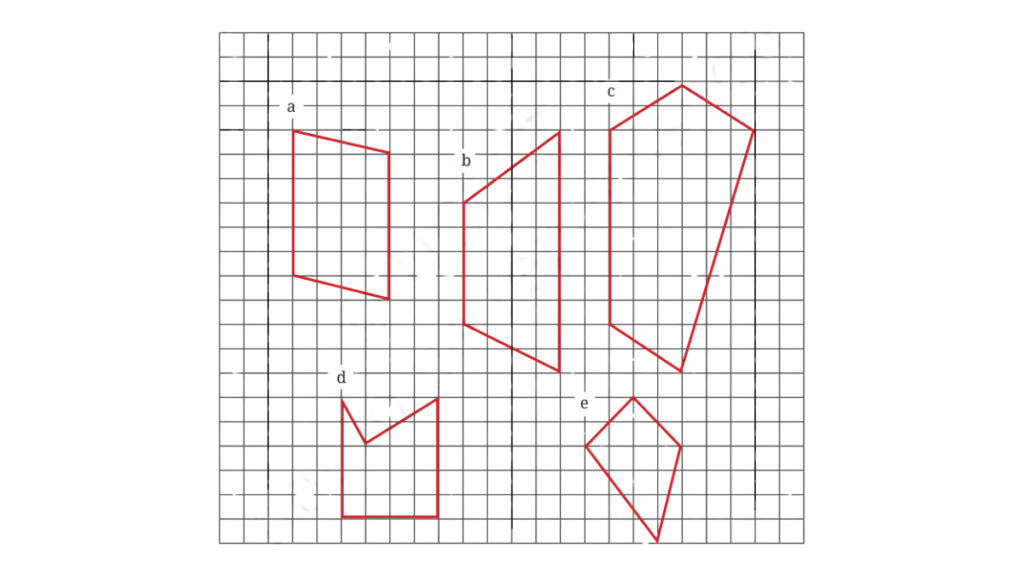
Answer:
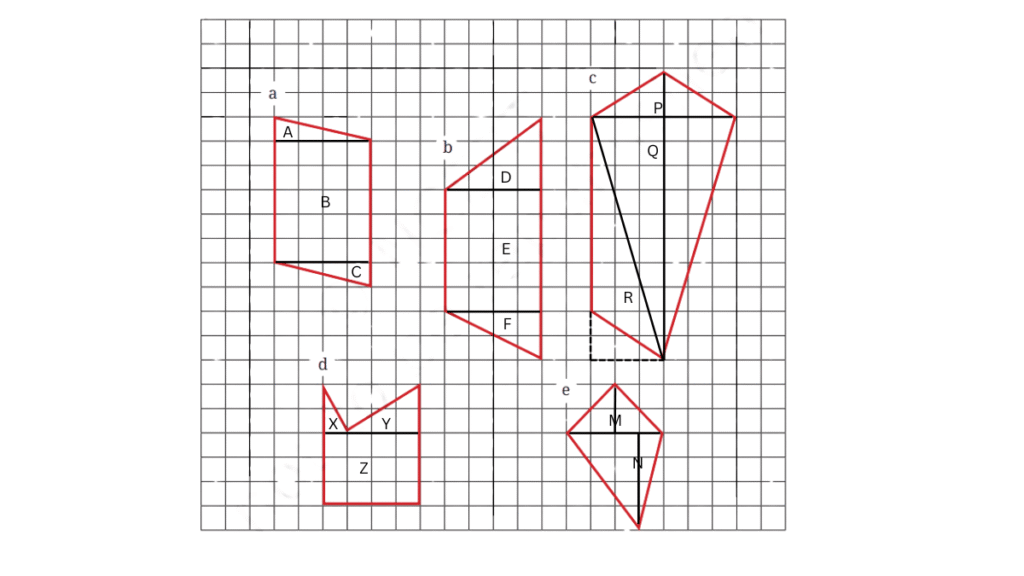
Figure (a):
Area of Triangle A = (1/2) × 1 × 4 = 2 sq. units
Area of Triangle C = (1/2) × 1 × 4 = 2 sq. units
Area of Rectangle B = 5 × 4 = 20 sq. units
Area of Figure (a) = 2 + 2 + 20 = 24 sq. units.
Figure (b):
Area of Triangle D = (1/2) × 3 × 4 = 6 sq. units
Area of Triangle F = (1/2) × 2 × 4 = 4 sq. units
Area of Rectangle E = 5 × 4 = 20 sq. units
Area of Figure (b) = 6 + 4 + 20 = 30 sq. units.
Figure (c):
Area of Triangle P = (1/2) × 2 × 6 = 6 sq. units.
Area of Triangle Q = (1/2) × 10 × 6 = 30 sq. units.
Area of Triangle R = (1/2) × 3 × 8 = 12 sq. units
Area of Figure (c) = 6 + 30 + 12 = 48 sq. units
Figure (d):
Area of Triangle X = (1/2) × 1 × 2 = 1 sq. units
Area of Triangle Y = (1/2) × 2 × 3 = 3 sq. units
Area of Rectangle Z = 4 × 3 = 12 sq. units
Area of Figure (d) = 1 + 3 + 12 = 16 sq. units
Figure (e):
Area of Triangle M = (1/2) × 4 × 2 = 4 sq. units
Area of Triangle N = (1/2) × 4 × 4 = 8 sq. units
Area of Figure (e) = 4 + 8 = 12 sq. units
Page 145:
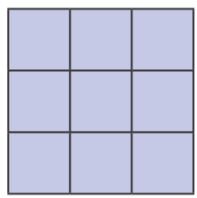
Using 9 unit squares, solve the following.
1. What is the smallest perimeter possible?
2. What is the largest perimeter possible?
3. Make a figure with a perimeter of 18 units.
4. Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter? What is your reasoning?
Answer:
1. What is the smallest perimeter possible?
The smallest perimeter is 12 units.
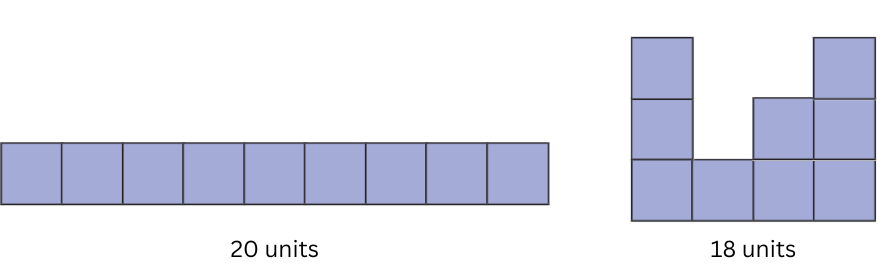
2. What is the largest perimeter possible?
The largest perimeter possible is 20 units.

3. Make a figure with a perimeter of 18 units.
A figure with a perimeter of 18 units is shown below:

4. Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter? What is your reasoning?
You cannot make other shaped figures for the smallest perimeter of 12 units, only one shape is possible. All other shapes have a greater number of exposed surfaces, hence have a larger perimeter.
Other shaped figures for perimeters of 20 units and 18 units are shown below:
Page 145:
Let’s do something tricky now! We have a figure below having perimeter 24 units.
Without calculating all over again, observe, think and find out what will be the change in the perimeter if a new square is attached as shown on the right.
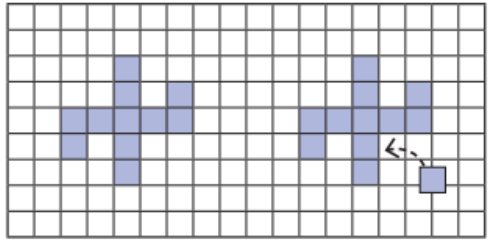
Answer:
There will be no change in perimeter.
Reason: The new square covers two sides of the figure and forms two new sides. Therefore, there is not change in the net perimeter.
Page 146:
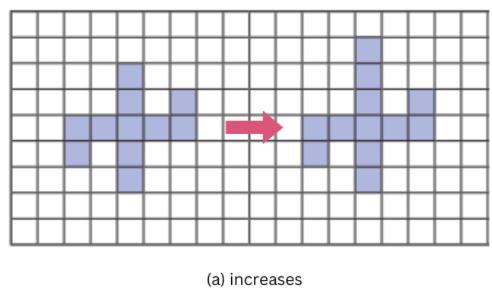
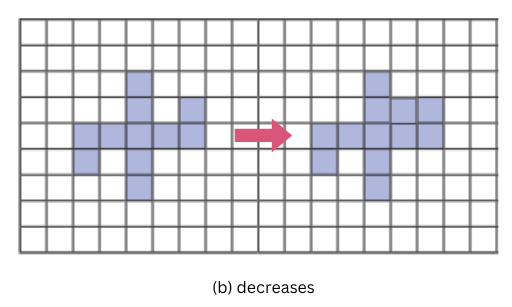
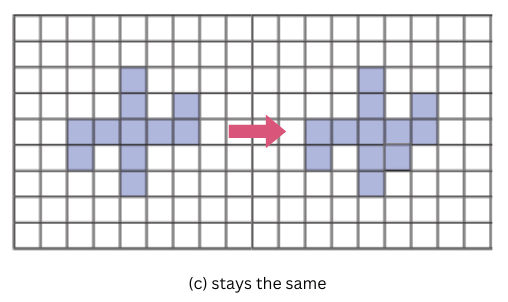
Experiment placing this new square at different places and think what the change in perimeter will be. Can you place the square so that the perimeter: a) increases; b) decreases; c) stays the same?
Answer:
a) increases
b) decreases
c) stays the same
Page 146:
Below is the house plan of Charan. It is in a rectangular plot. Look at the plan. What do you notice?
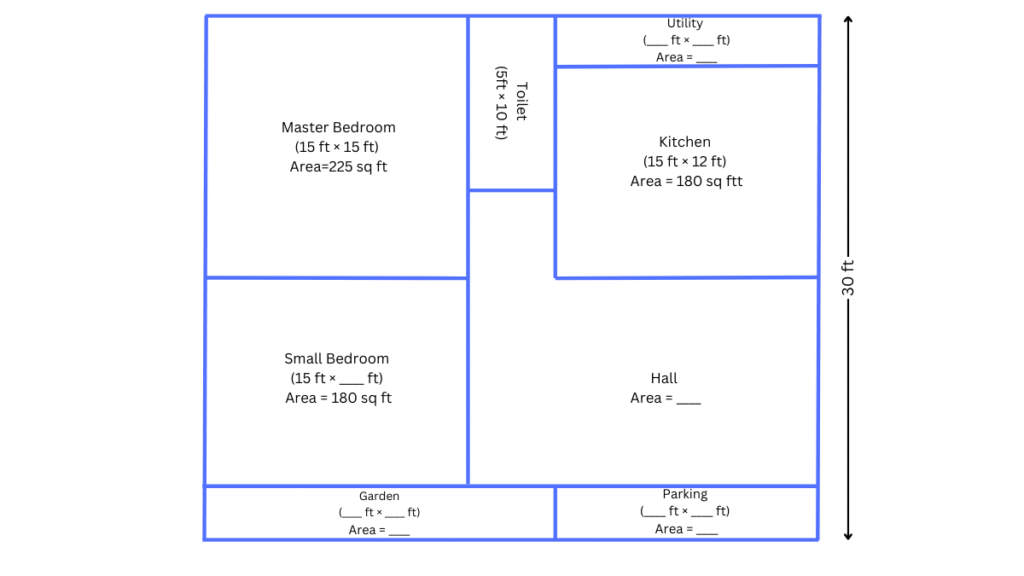
Some of the measurements are given.
a. Find the missing measurements.
b. Find out the area of his house.
Answer:
a. The missing measurements are given below:
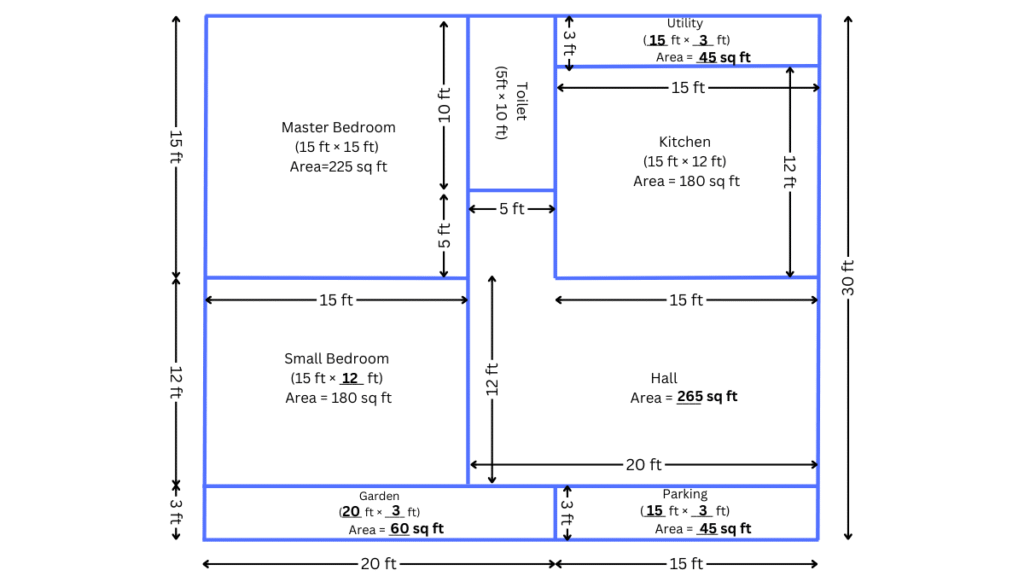
b. Area of his house = Length × Breadth = 35 × 30 = 1050 sq. ft.
Perimeter = 2(Length + Breadth) = 2(35 + 30) = 130 ft.
Page 147:
Now, find out the missing dimensions and area of Sharan’s home. Below is the plan:
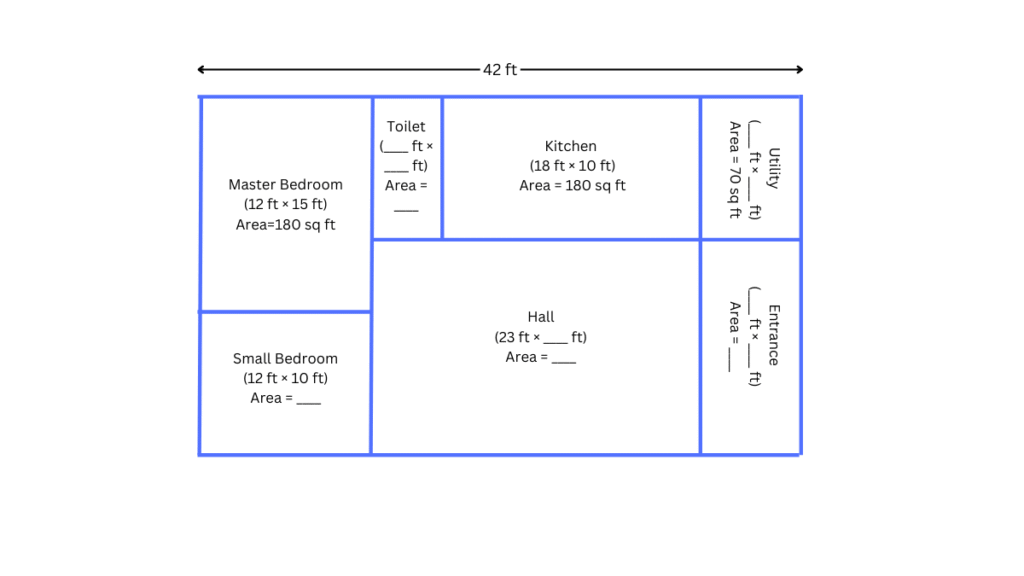
Some of the measurements are given.
a. Find the missing measurements.
b. Find out the area of his house.
What are the dimensions of all the different rooms in Sharan’s house? Compare the areas and perimeters of Sharan’s house and Charan’s house.
Answer:
a. The missing measurements are given below:

b. The area of his house = Length × Breadth = 42 ft × 25 ft = 1050 sq. ft.
Perimeter = 2(Length + Breadth) = 2(42 + 25) = 134 ft.
The dimensions of all the different rooms in Sharan’s house are given above in the diagram.
The areas and perimeters of Sharan’s house and Charan’s house is shown below:
| Sharan’s house | Charan’s house | |
| Areas (sq.ft) | 1050 | 1050 |
| Perimeters (ft) | 134 | 135 |
Page 148:
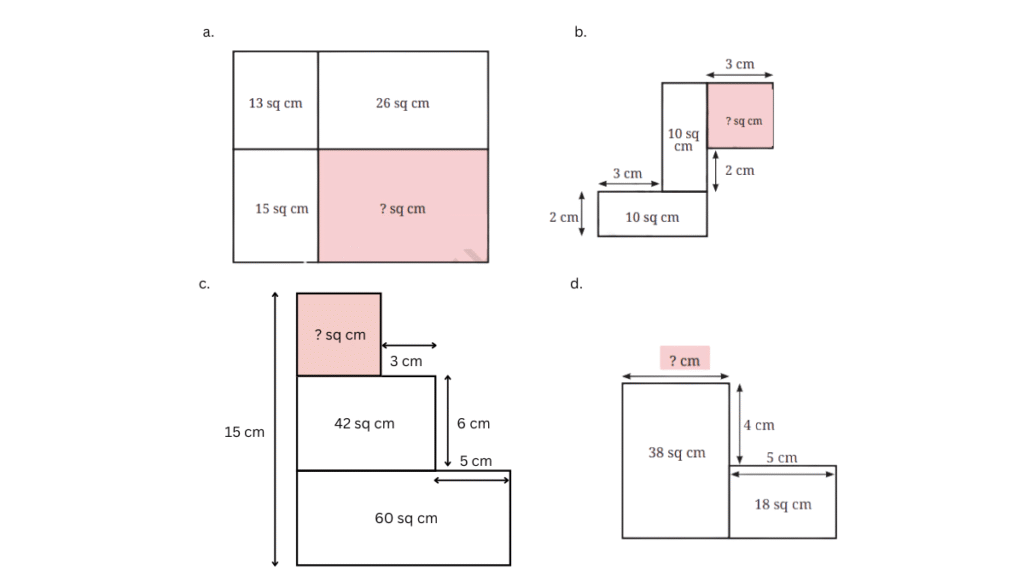
In each figure, find the missing value of either the length of a side or the area of a region.
Answer:
a.
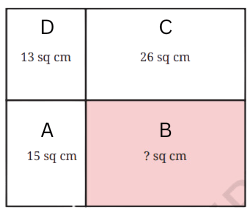
C has twice the area of D.
Therefore, B has twice the area of A = 15 × 2 = 30 sq. cm.
b.

For rectangle ABCD:
Area = 10 sq. cm
AD = 2 cm
DC = ?
Length × Breadth = Area
DC × AD = 10
DC × 2 = 10
DC = 10/2 = 5 cm
PC = DC – DP = 5 – 3 = 2 cm
For rectangle PCRQ:
PC = 2 cm
RC = ?
Length × Breadth = Area
RC × PC = 10
RC × 2 = 10
RC = 10/2 = 5 cm
RO = RC – OC = 5 – 2 = 3 cm
For RONM:
RO = 3 cm
RM = 3 cm
Therefore, it is a square
Area = Length × Length
Area = 3 × 3 = 9 sq. cm
c.

Answer:
For rectangle DPQS:
Area = 42 sq. cm
PQ = 6 cm
SQ = ?
Length × Breadth = Area
DP × PQ = 42
DP × 6 = 42
DP = 42/6 = 7 cm
SQ = DP = 7 cm
SR = 7 – 3 = 4 cm
For rectangle ABCD:
DC = DP + PC = 7 + 5 = 12 cm
AB = DC = 12 cm
Length × Breadth = Area
AB × BC = 60
12 × BC = 60
BC = 60/12 = 5 cm
Now,
AN = AD + DS + SN = BC + PQ + RM
AN = BC + PQ + RM
15 = 5 + 6 + RM
RM = 15 – 11 = 4 cm
For SRMN:
SR = 4 cm
RM = 4 cm
SRMN is a square.
Area = Length × Length = 4 × 4 = 16 sq. cm
d.
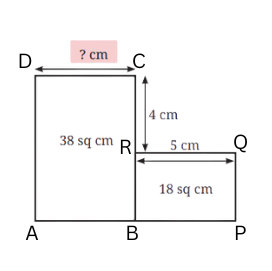
Answer:
For rectangle BPQR:
Length × Breadth = Area
QR × BR = 18
5 × BR = 18
BR = 18/5 = 3.6
BC = BR + RC = 3.6 + 4 = 7.6 cm
For rectangle ABCD:
BC × DC = 38
7.6 × DC = 38
DC = 38/7.6 = 5 cm
Figure it Out (Page 149):
1. Give the dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements: 5 m × 10 m and 2 m × 7 m.
Answer:
Sum of areas of both rectangles = 5 m × 10 m + 2 m × 7 m = 50 + 14 = 64 sq. m.
Therefore, the area of the rectangle whose area is the sum of the areas of these two rectangles = 64 sq. m.
Area = Length × Breadth
We can write,
64 = 16 × 4
Therefore, the length can be = 16 m and breadth = 4 m.
2. The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.
Answer:
Area = 1000 sq. m
Length = 50 m
Width = ?
Area = Length × Width
1000 = 50 × Width
Width = 1000/50 = 20 m
The width of the garden = 20 m.
3. The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.
Answer:
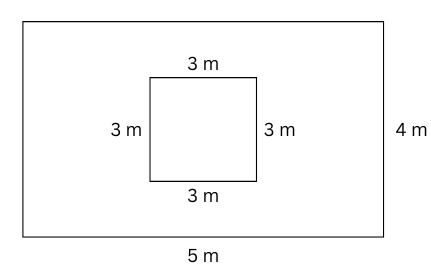
Length of the floor of the room = 5 m.
Width of the floor of the room = 4 m.
Area of the room = Length × Width = 5 × 4 = 20 sq. m.
Length of side of square carpet = 3 m.
Area of the square carpet = Length × Length = 3 × 3 = 9 sq. m.
Therefore, the area that is not carpeted = (20 – 9) sq. m = 11 sq. m.
4. Four flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?
Answer:
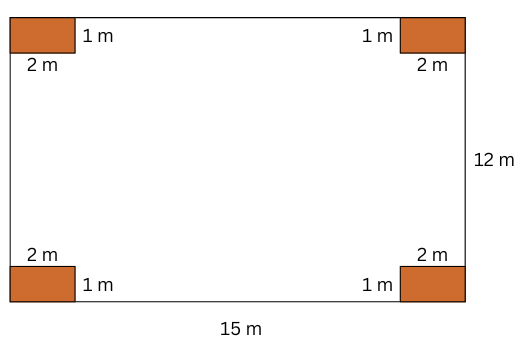
Length of the garden = 15 m.
Width of the garden = 12 m.
Area of the garden = 15 m × 12 m = 180 sq. m.
Length of each flower bed = 2 m.
Width of each flower bed = 1 m
Area of each flower bed = 2 × 1 = 2 sq. m.
Total area of four flower beds = (4 × 2) sq. m = 8 sq. m.
Area available for laying down a lawn = (180 – 8) sq. m = 172 sq. m.
5. Shape A has an area of 18 square units and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.
Answer:
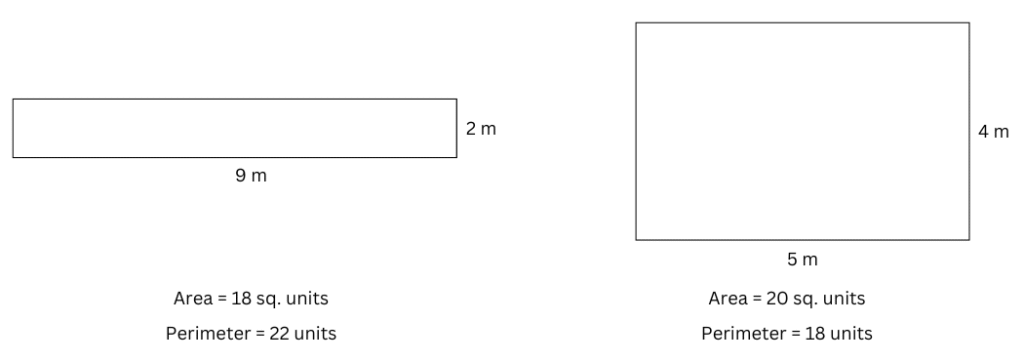
Perimeter of Shape A = (9 + 9 + 2 + 2) units = 22 units.
Perimeter of Shape B = (5 + 4 + 5 + 4) units = 18 units.
6. On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?
Answer:
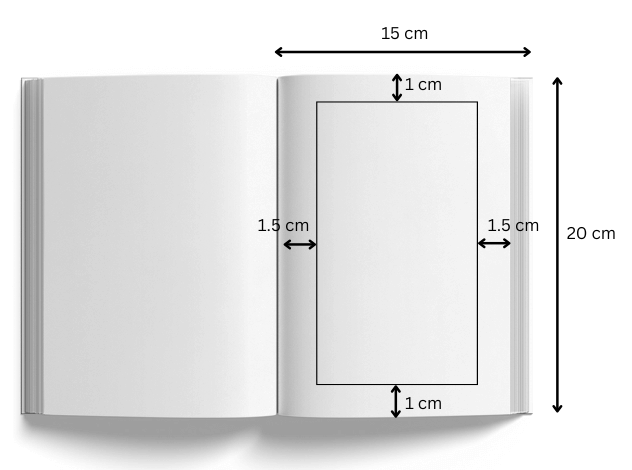
Length of the border = (20 – 1 – 1) cm = 18 cm.
Breadth of the border = (15 – 1.5 – 1.5) cm = 12 cm.
Perimeter of the rectangular border = 2(length + breadth) = 2(18 + 12) = 60 cm.
7. Draw a rectangle of size 12 units × 8 units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.
Answer:
Length of outer rectangle = 12 units.
Breadth of outer rectangle = 8 units.
Area of outer rectangle = Length × Breadth = 12 × 8 = 96 sq. units.
Area of inner rectangle = (1/2) × 96 = 48 sq. units.
We can write, 48 = 8 × 6
Therefore, length of inner rectangle = 8 units and breadth = 6 units.
The required figure is shown below:

8. A square piece of paper is folded in half. The square is then cut into two rectangles along the fold. Regardless of the size of the square, one of the following statements is always true. Which statement is true here?
a. The area of each rectangle is larger than the area of the square.
b. The perimeter of the square is greater than the perimeters of both the rectangles added together.
c. The perimeters of both the rectangles added together is always 1 1/2 times the perimeter of the square.
d. The area of the square is always three times as large as the areas of both rectangles added together.
Answer: c. The perimeters of both the rectangles added together is always 1 1/2 times the perimeter of the square.
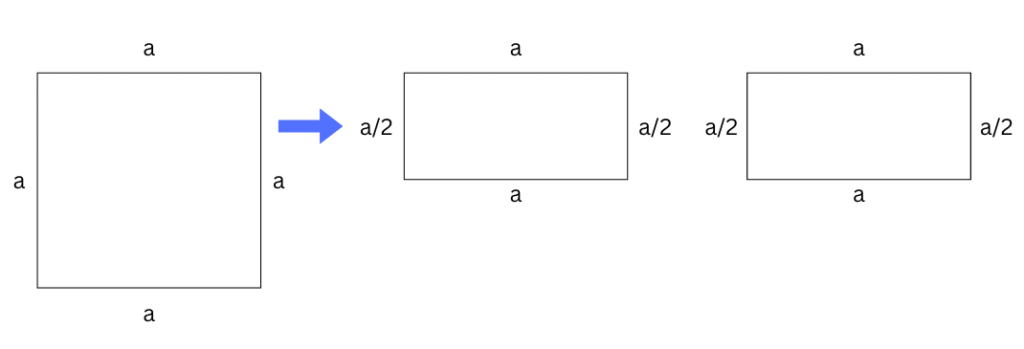
Perimeter of square = 4a.
Perimeter of each rectangle = (a/2 + a + a/2 + a) = 3a.
Perimeter of both rectangles added together = (3a + 3a) = 6a.
Therefore,
Perimeter of both rectangles added together/Perimeter of the square = 6a/4a = 3/2 = 1 ½.
Therefore, option (c) is True.


