Hello students and welcome to yet another amazing chapter on equations! Find top-quality solutions to Chapter 10 right here along with a set of extra problems of many formats. We have designed these to help clear your concepts and prepare you for your exams. Feel free to go through them in detail and benefit from them.
Solutions to Exercise 10.1 (Page No 165) of NCERT Class 7 Math Chapter 10 Algebraic Expressions –
1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
Answer: Correct expression: y – z
(ii) One-half of the sum of numbers x and y.
Answer: Sum of numbers x and y = (x + y)
One-half of the sum = 1/2 × (x + y)
Correct expression: (x + y)/2
(iii) The number z multiplied by itself.
Answer: The number z multiplied by itself = z × z = z2
Correct expression: z2
(iv) One-fourth of the product of numbers p and q.
Answer: Product of numbers p and q = (p × q)
One-fourth of the product = 1/4 × (p × q)
Correct expression: (p + q)/4
(v) Numbers x and y both squared and added.
Answer: The number x squared = x2
The number y squared = y2
The sum = (x2 + y2)
Correct expression: x2 + y2
(vi) Number 5 added to three times the product of numbers m and n.
Answer: The product of numbers m and n = m × n
Three times the product = 3 × m × n = 3mn
Number 5 added to three times the product = 3mn + 5
Correct expression: 3mn + 5
(vii) Product of numbers y and z subtracted from 10.
Answer: Product of numbers y and z = y × z = yz
Product of numbers y and z subtracted from 10 = 10 – yz
Correct expression: 10 – yz
(viii) Sum of numbers a and b subtracted from their product.
Answer: Sum of numbers a and b = (a + b)
Product of numbers a and b = a × b
The sum subtracted from the product = a × b – (a + b)
Correct expression: ab – (a + b)
2. (i) Identify the terms and their factors in the following expressions.
Show the terms and factors by tree diagrams.
(a) x – 3
Answer: The expression (x – 3) consists of two terms x and (-3).
Both the terms x and (-3) cannot be factorised further.
The tree diagram for the expression (x – 3) is shown below:

(b) 1 + x + x2
Answer: The expression (1 + x + x2) consists of three terms: 1, x, x2.
The terms 1 and x cannot be factorised further. We factorise the term x2 until it cannot be factorised further. Therefore, x2 can be written as: (x) × (x)
The tree diagram for the expression (1 + x + x2) is shown below:
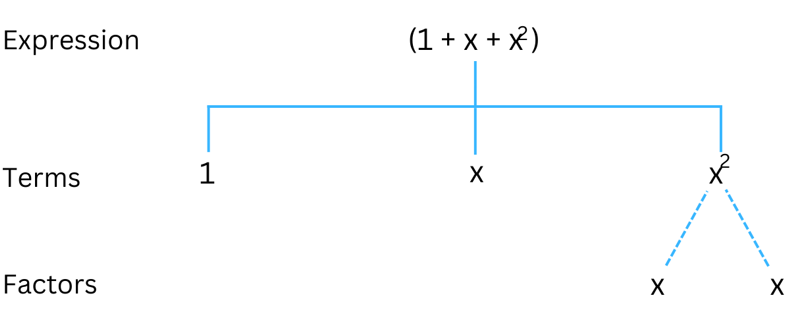
(c) y – y3
Answer: The expression (y – y3) consists of two terms: y, –y3.
The term y cannot be factorised further. We factorise the term –y3 until it cannot be factorised further. Therefore, –y3 can be written as: (-1) × (y) × (y) × (y)
The tree diagram for the expression (y – y3) is shown below:

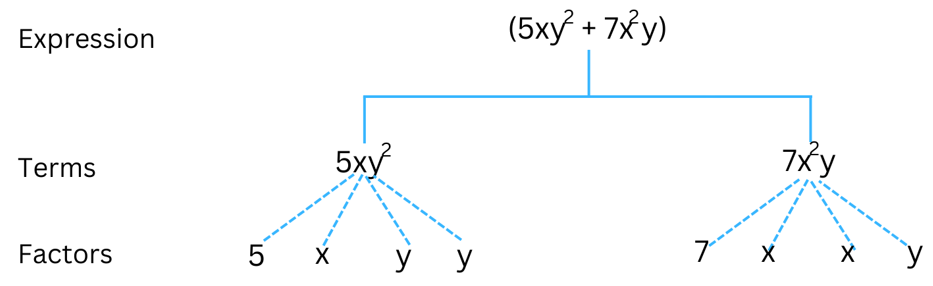
(d) 5xy2 + 7x2y
Answer: The expression (5xy2 + 7x2y) consists of two terms: 5xy2, 7x2y.
We factorise the term: 5xy2 until it cannot be factorised further. Therefore, 5xy2 can be written as: (5) × (x) × (y) × (y)
We factorise the term 7x2y until it cannot be factorised further. Therefore, 7x2y can be written as: (7) × (x) × (x) × (y)
The tree diagram for the expression (5xy2 + 7x2y) is shown below:
(e) – ab + 2b2 – 3a2
Answer: The expression (–ab + 2b2 – 3a2) consists of two terms: –ab, 2b2, –3a2.
We factorise the term: –ab until it cannot be factorised further. Therefore, –ab can be written as: (-1) × (a) × (b)
We factorise the term 2b2 until it cannot be factorised further. Therefore, 2b2 can be written as: (2) × (b) × (b)
We factorise the term -3a2 until it cannot be factorised further. Therefore, -3a2 can be written as: (-3) × (a) × (a)
The tree diagram for the expression (–ab + 2b2 – 3a2) is shown below:

(ii) Identify terms and factors in the expressions given below:
(a) – 4x + 5 (b) – 4x + 5y (c) 5y + 3y2
(d) xy + 2x2y2 (e) pq + q (f) 1.2ab – 2.4b + 3.6a
(g) x +
(h) 0.1 p2 + 0.2 q2
Answer:
Terms are added (not subtracted) to form expressions. If there is a minus sign (–) in the expression it is included in the term right after the sign.
The factors are such that they cannot be further factorised.
The table with the terms and factors for all the expressions is given below:
| Expressions | Terms | Factors | |
| (a) | –4x + 5 | –4x | -4, x |
| 5 | 5 | ||
| (b) | –4x + 5y | –4x | -4, x |
| 5y | 5, y | ||
| (c) | 5y + 3y2 | 5y | 5, y |
| 3y2 | 3, y, y | ||
| (d) | xy + 2x2y2 | xy | x, y |
| 2x2y2 | 2, x, x, y, y | ||
| (e) | pq + q | pq | p, q |
| q | q | ||
| (f) | 1.2ab – 2.4b + 3.6a | 1.2ab | 1.2, a, b |
| –2.4b | –2.4, b | ||
| 3.6a | 3.6, a | ||
| (g) | (3/4)x + 1/4 | (3/4)x | 3/4, x |
| 1/4 | 1/4 | ||
| (h) | 0.1 p2 + 0.2 q2 | 0.1 p2 | 0.1, p, p |
| 0.2 q2 | 0.2, q, q |
3. Identify the numerical coefficients of terms (other than constants) in the following expressions.
(i) 5 – 3t2 (ii) 1 + t + t2 + t3 (iii) x + 2xy + 3y
(iv) 100m + 1000n (v) – p2q2 + 7pq (vi) 1.2 a + 0.8 b
(vii) 3.14 r2 (viii) 2 (l + b) (ix) 0.1 y + 0.01 y2
Answer:
A term can be written as a product of factors. One of them is numerical and the others are algebraic. The numerical factor is said to be the coefficient of the term.
The table with the numerical coefficients of terms (other than constant terms) for all expressions is shown below:
| Expressions | Terms (not including constant terms) | Numerical Coefficient | |
| (i) | 5 – 3t2 | –3t2 | -3 |
| (ii) | 1 + t + t2 + t3 | t | 1 |
| t2 | 1 | ||
| t3 | 1 | ||
| (iii) | x + 2xy + 3y | x | 1 |
| 2xy | 2 | ||
| 3y | 3 | ||
| (iv) | 100m + 1000n | 100m | 100 |
| 1000n | 1000 | ||
| (v) | – p2q2 + 7pq | – p2q2 | -1 |
| 7pq | 7 | ||
| (vi) | 1.2 a + 0.8 b | 1.2 a | 1.2 |
| 0.8 b | 0.8 | ||
| (vii) | 3.14 r2 | 3.14 r2 | 3.14 |
| (viii) | 2 (l + b) | 2l | 2 |
| 2b | 2 | ||
| (ix) | 0.1 y + 0.01 y2 | 0.1 y | 0.1 |
| 0.01 y2 | 0.01 |
4. (a) Identify terms which contain x and give the coefficient of x.
(i) y2x + y (ii) 13y2 – 8yx (iii) x + y + 2
(iv) 5 + z + zx (v) 1 + x + xy (vi) 12xy2 + 25
(vii) 7x + xy2
Answer:
Generally speaking, a coefficient may be either a numerical factor or an algebraic factor or even a product of two or more factors.
Here in each expression we look for a term with x as factor. The remaining part of the term is the coefficient of x.
The correct table is shown below:
| Expressions | Terms which contain x | Coefficient of x | |
| (i) | y2x + y | y2x | y2 |
| (ii) | 13y2 – 8yx | –8yx | –8y |
| (iii) | x + y + 2 | x | 1 |
| (iv) | 5 + z + zx | zx | z |
| (v) | 1 + x + xy | x | 1 |
| xy | y | ||
| (vi) | 12xy2 + 25 | 12xy2 | 12y2 |
| (vii) | 7x + xy2 | 7x | 7 |
| xy2 | y2 |
(b) Identify terms which contain y2 and give the coefficient of y2.
(i) 8 – xy2 (ii) 5y2 + 7x (iii) 2x2y – 15xy2 + 7y2
Answer:
Here in each expression we look for a term with y2 as factor. The remaining part of the term is the coefficient of x.
The correct table is shown below:
| Expressions | Terms which contain y2 | Coefficient of y2 | |
| (i) | 8 – xy2 | –xy2 | –x |
| (ii) | 5y2 + 7x | 5y2 | 5 |
| (iii) | 2x2y – 15xy2 + 7y2 | –15xy2 | –15x |
| 7y2 | 7 |
5. Classify into monomials, binomials and trinomials.
(i) 4y – 7z (ii) y2 (iii) x + y – xy (iv) 100
(v) ab – a – b (vi) 5 – 3t (vii) 4p2q – 4pq2 (viii) 7mn
(ix) z2 – 3z + 8 (x) a2 + b2 (xi) z2 + z (xii) 1 + x + x2
Answer:
A monomial is an expression which contains only one term.
A binomial is an expression which contains two unlike terms.
A trinomial is an expression which contains three unlike terms.
The table with the correct classifications is shown below:
| Expressions | Classification | Remarks |
| (i) 4y – 7z | Binomial | There are two unlike terms because the variables in the terms are different. |
| (ii) y2 | Monomial | There is only one term in the expression. |
| (iii) x + y – xy | Trinomial | There are three unlike terms because the algebraic factors in the terms are different. |
| (iv) 100 | Monomial | There is only one term in the expression. |
| (v) ab – a – b | Trinomial | There are three unlike terms because the algebraic factors in the terms are different. |
| (vi) 5 – 3t | Binomial | There are two unlike terms because one is a constant and the other contains a variable. |
| (vii) 4p2q – 4pq2 | Binomial | There are two unlike terms because the algebraic factors in the terms are different. |
| (viii) 7mn | Monomial | There is only one term in the expression. |
| (ix) z2 – 3z + 8 | Trinomial | There are three unlike terms because the algebraic factors in the first two terms are different and the third is a constant. |
| (x) a2 + b2 | Binomial | There are two unlike terms because the algebraic factors in the terms are different. |
| (xi) z2 + z | Binomial | There are two unlike terms because the algebraic factors in the terms are different. |
| (xii) 1 + x + x2 | Trinomial | There are three unlike terms because the first term is a constant and the algebraic factors in the second and third terms are different |
6. State whether a given pair of terms is of like or unlike terms.
(i) 1, 100 (ii) –7x, (5/2)x (iii) – 29x, – 29y
(iv) 14xy, 42yx (v) 4m2p, 4mp2 (vi) 12xz, 12x2z2
Answer:
Like terms have the same algebraic factors.
Unlike terms have different algebraic factors.
The correct classification is shown below:
| S.No | Pair | Factors | Algebraic factors same or different | Like/Unlike terms | Remarks |
| (i) | 1 100 | 1 100 | Not applicable | Like | They are both constant terms, no algebraic factors |
| (ii) | –7x (5/2)x | –7, x | Same | Like | x is the common algebraic factor. |
| (iii) | –29x –29y | –29, x –29, y | Different | Unlike | The variables in the terms are different. |
| (iv) | 14xy 42yx | 14, x, y 42, y, x | Same | Like | Remember xy = yx |
| (v) | 4m2p 4mp2 | 4, m, m, p 4, m, p, p | Different | Unlike | The variables in the two terms match, but their powers do not match. |
| (vi) | 12xz 12x2z2 | 12, x, z 12, x, x, z, z | Different | Unlike | The variables in the two terms match, but their powers do not match. |
7. Identify like terms in the following:
(a) – xy2, – 4yx2, 8x2, 2xy2, 7y, – 11x2, – 100x, – 11yx, 20x2y, – 6x2, y, 2xy, 3x
Answer:
Like terms have the same algebraic factors.
Therefore,
– xy2, 2xy2 are like terms (Both have the same algebraic factor xy2)
– 4yx2, 20x2y are like terms (Both have the same algebraic factor yx2 = x2y)
8x2, – 11x2, – 6x2 are like terms (Both have the same algebraic factor x2)
7y, y are like terms (Both have the same algebraic factor y)
– 100x, 3x are like terms (Both have the same algebraic factor x)
– 11yx, 2xy are like terms (Both have the same algebraic factor yx = xy)
(b) 10pq, 7p, 8q, – p2q2, – 7qp, – 100q, – 23, 12q2p2, – 5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
Answer:
Like terms have the same algebraic factors.
Therefore,
10pq, – 7qp, 78qp are like terms (Both have the same algebraic factor pq = qp)
7p, 2405p are like terms (Both have the same algebraic factor p)
8q, – 100q are like terms (Both have the same algebraic factor q)
– p2q2, 12q2p2 are like terms (Both have the same algebraic factor p2q2 = q2p2)
– 23, 41 are like terms (They are both constant terms, no algebraic factors)
– 5p2, 701p2 are like terms (Both have the same algebraic factor p2)
13p2q, qp2 are like terms (Both have the same algebraic factor p2q = qp2)
Solutions to Exercise 10.2 (Page No 168) of NCERT Class 7 Math 10 Algebraic Expressions –
1. If m = 2, find the value of:
(i) m – 2 (ii) 3m – 5 (iii) 9 – 5m
(iv) 3m2 – 2m – 7 (v) 5m/2 – 4
Answer:
(i) Putting m = 2 in (m – 2), we get the value of (m – 2) = 2 – 2 = 0.
(ii) Putting m = 2 in (3m – 5), we get the value of (3m – 5) = 3 × 2 – 5 = 6 – 5 = 1.
(iii) Putting m = 2 in (9 – 5m), we get the value of (9 – 5m) = 9 – 5 × 2 = 9 – 10 = -1.
(iv) Putting m = 2 in (3m2 – 2m – 7), we get the value of (3m2 – 2m – 7) as:
3m2 – 2m – 7
= (3 × 22) – 2 × 2 – 7
= (3 × 4) – 4 – 7
= 12 – 11
= 1
(v) Putting m = 2 in (5m/2 – 4), we get the value of (5m/2 – 4) as:
5m/2 – 4
= (5 × 2)/2 – 4
= 5 – 4
= 1
2. If p = – 2, find the value of:
(i) 4p + 7
Answer: Putting the value of p = -2, in 4p + 7, we get,
4 × (-2) + 7 = – 8 + 7 = -1
(ii) – 3p2 + 4p + 7
Answer: For p = -2 we have:
4p + 7 = 4 × (-2) + 7 = -8 + 7 = -1
– 3p2 = -3 × (-2)2 = -3 × 4 = -12
Combining,
– 3p2 + 4p + 7 = -12 – 1 = -13
(iii) – 2p3 – 3p2 + 4p + 7
Answer:
For p = -2 we found earlier:
– 3p2 + 4p + 7 = -13
-2p3 = -2 × (-2)3 = (-2) × (-8) = 16
Combining,
– 2p3 – 3p2 + 4p + 7 = 16 – 13 = 3
3. Find the value of the following expressions, when x = –1:
(i) 2x – 7
Answer:
Putting the value of x = -1 in (2x – 7) we get:
2x – 7
= 2 × (-1) – 7
= – 2 – 7
= -9.
(ii) – x + 2
Answer:
Putting the value of x = -1 in (– x + 2) we get:
– x + 2
= – (– 1) + 2
= 1 + 2
= 3
(iii) x2 + 2x + 1
Answer:
Putting the value of x = -1 in (x2 + 2x + 1) we get:
x2 + 2x + 1
= (-1)2 + 2 × (-1) + 1
= 1 – 2 + 1
= 0
(iv) 2x2 – x – 2
Answer:
Putting the value of x = -1 in (2x2 – x – 2) we get:
2x2 – x – 2
= 2 × (-1)2 – (-1) – 2
= 2 + 1 – 2 = 1
4. If a = 2, b = – 2, find the value of:
(i) a2 + b2
Answer:
Substituting a = 2 and b = – 2 in (a2 + b2) we get:
a2 + b2
= (2)2 + (-2)2
= 4 + 4
= 8
(ii) a2 + ab + b2
Answer:
Substituting a = 2 and b = – 2 in (a2 + ab + b2) we get:
a2 + ab + b2
= (2)2 + (2) × (-2) + (-2)2
= 4 + (-4) + 4
= 4
(iii) a2 – b2
Answer:
Substituting a = 2 and b = – 2 in (a2 – b2) we get:
a2 – b2
= (2)2 – (-2)2
= 4 – (4)
= 0
5. When a = 0, b = – 1, find the value of the given expressions:
(i) 2a + 2b
Answer:
Substituting a = 0 and b = – 1 in (2a + 2b) we get:
2a + 2b
= 2 × (0) + 2 × (-1)
= 0 – 2
= – 2
(ii) 2a2 + b2 + 1
Answer:
Substituting a = 0 and b = – 1 in (2a2 + b2 + 1) we get:
2a2 + b2 + 1
= 2 × (0)2 + (-1)2 + 1
= 0 + 1 + 1
= 2
(iii) 2a2b + 2ab2 + ab
Answer:
Substituting a = 0 and b = – 1 in (2a2b + 2ab2 + ab) we get:
2a2b + 2ab2 + ab
= 2 × (0)2 × (-1) + 2 × (0) × (-1)2 + (0) × (-1)
= 0 + 0 + 0
= 0
(iv) a2 + ab + 2
Answer:
Substituting a = 0 and b = – 1 in (a2 + ab + 2) we get:
a2 + ab + 2
= (0)2 + (0) × (-1) + 2
= 0 + 0 + 2= 2
6. Simplify the expressions and find the value if x is equal to 2
(i) x + 7 + 4 (x – 5)
Answer:
Simplifying we get,
x + 7 + 4 (x – 5)
= x + 7 + 4x – 20
= x + 4x + 7 – 20 (Grouping the like terms together)
= 5x – 13
Substituting x = 2 in (5x – 13) we get:
5x – 13
= 5 × 2 – 13
= 10 – 13
= – 3
(ii) 3 (x + 2) + 5x – 7
Answer:
Simplifying we get,
3 (x + 2) + 5x – 7
= 3x + 6 + 5x – 7
= 3x + 5x + 6 – 7 (Grouping the like terms together)
= 8x – 1
Substituting x = 2 in (8x – 1) we get:
8x – 1
= 8 × 2 – 1
= 16 – 1
= 15
(iii) 6x + 5 (x – 2)
Answer:
Simplifying we get,
6x + 5 (x – 2)
= 6x + 5x – 10
= 11x – 10
Substituting x = 2 in (11x – 10) we get:
11x – 10
= 11 × 2 – 10
= 22 – 10
= 12
(iv) 4(2x – 1) + 3x + 11
Answer:
Simplifying we get,
4(2x – 1) + 3x + 11
= 8x – 4 + 3x + 11
= 8x + 3x – 4 + 11 (Grouping the like terms together)
= 11x + 7
Substituting x = 2 in (11x + 7) we get:
11x + 7
= 11 × 2 + 7
= 22 + 7= 29
7. Simplify these expressions and find their values if x = 3, a = – 1, b = – 2.
(i) 3x – 5 – x + 9
Answer:
Simplifying we get,
3x – 5 – x + 9
= 3x – x – 5 + 9 (Grouping the like terms together)
= 2x + 4
Substituting x = 3 in (2x + 4) we get:
2x + 4
= 2 × 3 + 4
= 6 + 4
= 10
(ii) 2 – 8x + 4x + 4
Answer:
Simplifying we get,
2 – 8x + 4x + 4
= 2 + 4 – 8x + 4x (Grouping the like terms together)
= 6 – 4x
Substituting x = 3 in (6 – 4x) we get:
6 – 4x
= 6 – 4 × 3
= 6 – 12
= – 6
(iii) 3a + 5 – 8a + 1
Answer:
Simplifying we get,
3a + 5 – 8a + 1
= 3a – 8a + 5 + 1 (Grouping the like terms together)
= – 5a + 6
Substituting a = -1 in (– 5a + 6) we get:
– 5a + 6
= – 5 × (– 1) + 6
= 5 + 6
= 11
(iv) 10 – 3b – 4 – 5b
Answer:
Simplifying we get,
10 – 3b – 4 – 5b
= 10 – 4 – 3b – 5b (Grouping the like terms together)
= 6 – 8b
Substituting b = -2 in (6 – 8b) we get:
6 – 8b
= 6 – 8 × (– 2)
= 6 + 16
= 22
(v) 2a – 2b – 4 – 5 + a
Answer:
Simplifying we get,
2a – 2b – 4 – 5 + a
= 2a + a – 2b – 4 – 5 (Grouping the like terms together)
= 3a – 2b – 9
Substituting a = -1 and b = -2 in (3a – 2b – 9) we get:
3a – 2b – 9
= 3 × (-1) – 2 × (-2) – 9
= -3 + 4 – 9 = -8
8. (i) If z = 10, find the value of z3 – 3(z – 10).
Answer:
z3 – 3(z – 10)
= z3 – 3z + 30 (Taking care of the signs while opening the bracket)
Substituting z = 10 in (z3 – 3z + 30) we get:
z3 – 3z + 30
= (10)3 – 3 × 10 + 30
= 1000 – 30 + 30
= 1000
(ii) If p = – 10, find the value of p2 – 2p – 100
Answer:
Substituting p = – 10 in (p2 – 2p – 100) we get:
p2 – 2p – 100
= (-10)2 – 2 × (-10) – 100
= 100 + 20 – 100 = 20
9. What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0?
Answer:
2x2 + x – a = 5
Substituting x = 0 into the equation we get,
2 × (0)2 + 0 – a = 5
or, 0 + 0 – a = 5
or, -a = 5
or, -a = 5
or, a = –5
10. Simplify the expression and find its value when a = 5 and b = – 3.
2(a2 + ab) + 3 – ab
Answer:
Simplifying the expression we get:
2(a2 + ab) + 3 – ab
= 2a2 + 2ab + 3 – ab
= 2a2 + 2ab – ab + 3
= 2a2 + ab + 3
Substituting a = 5 and b = -3 in (2a2 + ab + 3) we get:
2a2 + ab + 3
= 2 × (5)2 + (5) × (-3) + 3
= 2 × 25 + (-15) + 3
= 50 – 15 + 3
= 38
Important Questions from Previous NCERT Textbook:
Exercise 12.2 Page No 239 (Old Textbook):
1. Simplify combining like terms.
(i) 21b – 32 + 7b – 20b
Answer:
Like terms have the same algebraic factors.
Rearranging terms and collecting the like terms together, we have:
21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32
= (21 + 7 – 20)b – 32
= 8b – 32
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
Answer:
Like terms have the same algebraic factors.
Rearranging terms and collecting the like terms together, we have:
– z2 + 13z2 – 5z – 15z + 7z3
= 7z3 – z2 + 13z2 – 5z – 15z
= 7z3 + (-1 + 13) z2 + (-5 – 15)z
= 7z3 + (12)z2 + (–20)z
= 7z3 + 12z2 –20z
(iii) p – (p – q) – q – (q – p)
Answer:
Like terms have the same algebraic factors.
p – (p – q) – q – (q – p)
= p – p + q – q – q + p (Opening the brackets and taking care of the signs)
= p – p + p + q – q – q (Rearranging terms and collecting the like terms together)
= (1 – 1 + 1)p + (1 – 1 – 1)q
= (1)p + (-1)q
= p – q
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
Answer:
Like terms have the same algebraic factors.
3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a (Opening the brackets and taking care of the signs)
= 3a – a – a – 2b + b + b – ab – ab + 3ab (Rearranging terms and collecting the like terms together)
= (3 – 1 – 1)a + (-2 + 1 + 1)b + (-1 – 1 + 3)ab
= (1)a + (0)b + (1)ab
= a + ab
(v) 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
Answer:
Like terms have the same algebraic factors.
Rearranging terms and collecting the like terms together, we have:
5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
= 5x2y + 3yx2 – 5x2 + x2 – 3y2 – y2 – 3y2 + 8xy2
= (5 + 3)x2y + (-5 + 1)x2 + (-3 – 1 – 3)y2 + 8xy2
= (8)x2y + (-4)x2 + (-7)y2 + 8xy2
= 8x2y – 4x2 – 7y2 + 8xy2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
Answer:
Like terms have the same algebraic factors.
(3y2 + 5y – 4) – (8y – y2 – 4)
= 3y2 + 5y – 4 – 8y + y2 + 4 (Opening the brackets and taking care of the signs)
=3y2 + y2 + 5y – 8y – 4 + 4 (Rearranging terms and collecting the like terms together)
= (3 + 1)y2 + (5 – 8)y + (-4 + 4)
= (4)y2 + (-3)y + (0)= 4y2 – 3y
2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
Answer:
Like terms have the same algebraic factors.
The sum = 3mn + (– 5mn) + 8mn + (– 4mn)
= (3 – 5 + 8 – 4)mn
= (2)mn
= 2mn
(ii) t – 8tz, 3tz – z, z – t
Answer:
Like terms have the same algebraic factors.
The sum = (t – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= t – t – 8tz + 3tz – z + z (Rearranging terms and collecting the like terms together)
= (1 – 1)t + (-8 + 3)tz + (-1 + 1)z
= (0)t + (-5)tz + (0)z
= 0 – 5tz + 0
= – 5tz
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
Answer:
Like terms have the same algebraic factors.
The sum = (– 7mn + 5) + (12mn + 2) + (9mn – 8) + (– 2mn – 3)
=– 7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= – 7mn + 12mn + 9mn – 2mn + 5 + 2 – 8 – 3 (Rearranging terms and collecting the like terms together)
= (-7 + 12 + 9 – 2)mn + (5 + 2 – 8 – 3)
= (12)mn + (-4)
= 12mn – 4
(iv) a + b – 3, b – a + 3, a – b + 3
Answer:
Like terms have the same algebraic factors.
The sum = (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= a – a + a + b + b – b – 3 + 3 + 3 (Rearranging terms and collecting the like terms together)
= (1 – 1 + 1)a + (1 + 1 – 1)b + (-3 + 3 + 3)
= (1)a + (1)b + (3)
= a + b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
Answer:
Like terms have the same algebraic factors.
The sum = (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= 14x – 7x + 10y – 10y – 12xy + 8xy + 4xy – 13 + 18 (Rearranging terms and collecting the like terms together)
= (14 – 7)x + (10 – 10)y + (-12 + 8 + 4)xy + (-13 + 18)
= (7)x + (0)y + (0)xy + (5)
= 7x + 0 + 0 + 5
= 7x + 5
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
Answer:
Like terms have the same algebraic factors.
The sum = (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5 (Rearranging terms and collecting the like terms together)
= (5 – 4 + 2)m + (-7 + 3)n – 3mn + (2 – 5)
= (3)m + (-4)n – 3mn – 3
= 3m – 4n – 3mn – 3
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
Answer:
Like terms have the same algebraic factors.
The sum = (4x2y) + (– 3xy2) + (–5xy2) + (5x2y)
= 4x2y – 3xy2 – 5xy2 + 5x2y
= 4x2y + 5x2y – 3xy2 – 5xy2 (Rearranging terms and collecting the like terms together)
= (4 + 5)x2y + (-3 – 5)xy2
= (9)x2y + (-8)xy2
= 9x2y – 8xy2
(viii) 3p2q2 – 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
Answer:
Like terms have the same algebraic factors.
The sum = (3p2q2 – 4pq + 5) + (– 10 p2q2) + (15 + 9pq + 7p2q2)
= 3p2q2 – 4pq + 5 – 10 p2q2 + 15 + 9pq + 7p2q2
= 3p2q2 – 10p2q2 + 7p2q2 – 4pq + 9pq + 5 + 15 (Rearranging terms and collecting the like terms together)
= (3 – 10 + 7)p2q2 + (-4 + 9)pq + (5 + 15)
= (0)p2q2 + (5)pq + 20
= 0 + 5pq + 20
= 5pq + 20
(ix) ab – 4a, 4b – ab, 4a – 4b
Answer:
Like terms have the same algebraic factors.
The sum = (ab – 4a) + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= (ab – ab) + (-4a + 4a) + (4b – 4b) (Rearranging terms and collecting the like terms together)
= (0) + (0) + (0)
= 0
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
Answer:
Like terms have the same algebraic factors.
The sum = (x2 – y2 – 1) + (y2 – 1 – x2) + (1 – x2 – y2)
= x2 – y2 – 1 + y2 – 1 – x2 + 1 – x2 – y2
= (x2 – x2 – x2) + (– y2 + y2 – y2) + (-1 – 1 + 1) (Rearranging terms and collecting the like terms together)
= (– x2) + (– y2) + (-1)= – x2 – y2 – 1
3. Subtract:
(i) –5y2 from y2
Answer:
Like terms have the same algebraic factors.
y2 – (–5y2)
= y2 + 5y2 (Taking care of the signs while opening the bracket)
= (1 + 5)y2
= 6y2
(ii) 6xy from –12xy
Answer:
Like terms have the same algebraic factors.
–12xy – 6xy
= (-12 – 6)xy
= (-18)xy
= -18xy
(iii) (a – b) from (a + b)
Answer:
Like terms have the same algebraic factors.
(a + b) – (a – b)
= a + b – a + b (Taking care of the signs while opening the bracket)
= a – a + b + b (Rearranging terms and collecting the like terms together)
= (a – a) + (b + b)
= (0) + (2b)
= 2b
(iv) a(b – 5) from b(5 – a)
Answer:
Like terms have the same algebraic factors.
b(5 – a) – a(b – 5)
= 5b – ab – ab + 5a (Taking care of the signs while opening the bracket. The like terms are together, the unlike terms will remain as they are)
= 5b – 2ab + 5a
(v) –m2 + 5mn from 4m2 – 3mn + 8
Answer:
Like terms have the same algebraic factors.
(4m2 – 3mn + 8) – (–m2 + 5mn)
= 4m2 – 3mn + 8 + m2 – 5mn (Taking care of the signs while opening the bracket)
= 4m2 + m2 – 3mn – 5mn + 8 (Rearranging terms and collecting the like terms together)
= 5m2 – 8mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
Answer:
Like terms have the same algebraic factors.
(5x – 10) – (– x2 + 10x – 5)
= 5x – 10 + x2 – 10x + 5 (Taking care of the signs while opening the bracket)
= x2 – 10x + 5x – 10 + 5 (Rearranging terms and collecting the like terms together)
= x2 – 5x – 5
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
Answer:
Like terms have the same algebraic factors.
(3ab – 2a2 – 2b2) – (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2 (Taking care of the signs while opening the bracket)
= 3ab + 7ab – 2a2 – 5a2 – 2b2 – 5b2 (Rearranging terms and collecting the like terms together)
= 10ab – 7a2 – 7b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Answer:
Like terms have the same algebraic factors.
(5p2 + 3q2 – pq) – (4pq – 5q2 – 3p2)
= 5p2 + 3q2 – pq – 4pq + 5q2 + 3p2 (Taking care of the signs while opening the bracket)
= 5p2 + 3p2 + 3q2 + 5q2 – pq – 4pq (Rearranging terms and collecting the like terms together)
= 8p2 + 8q2 – 5pq
4. (a) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
Answer: We should subtract (x2 + xy + y2) from (2x2 + 3xy) to get the required result.
Like terms have the same algebraic factors.
(2x2 + 3xy) – (x2 + xy + y2)
= 2x2 + 3xy – x2 – xy – y2 (Taking care of the signs while opening the bracket)
= 2x2 – x2 + 3xy – xy – y2 (Rearranging terms and collecting the like terms together)
= x2 + 2xy – y2
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Answer: We should subtract (– 3a + 7b + 16) from (2a + 8b + 10) to get the required result.
Like terms have the same algebraic factors.
(2a + 8b + 10) – (– 3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16 (Taking care of the signs while opening the bracket)
= 2a + 3a + 8b – 7b + 10 – 16 (Rearranging terms and collecting the like terms together)
= 5a + b – 6
5. What should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20?
Answer: Like terms have the same algebraic factors.
(3x2 – 4y2 + 5xy + 20) – (– x2 – y2 + 6xy + 20)
= 3x2 – 4y2 + 5xy + 20 + x2 + y2 – 6xy – 20 (Taking care of the signs while opening the bracket)
= 3x2 + x2 – 4y2 + y2 + 5xy – 6xy + 20 – 20 (Rearranging terms and collecting the like terms together)
= 4x2 – 3y2 – xy
6. (a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.
Answer: We first add (3x – y + 11) and (– y – 11):
(3x – y + 11) + (– y – 11)
= 3x – y + 11 – y – 11 (Taking care of the signs while opening the bracket)
= 3x – y – y + 11 – 11 (Rearranging terms and collecting the like terms together)
= 3x + (-1 – 1)y + 0
= 3x + (-2)y
= 3x – 2y
Now, we subtract (3x – y – 11) from (3x – 2y):
(3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11 (Taking care of the signs while opening the bracket)
= 3x – 3x – 2y + y + 11 (Rearranging terms and collecting the like terms together)
= 0 – y + 11
= – y + 11
(b) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and –x2 + 2x + 5.
Answer: We first add (4 + 3x) and (5 – 4x + 2x2):
(4 + 3x) + (5 – 4x + 2x2)
= 4 + 3x + 5 – 4x + 2x2
= 4 + 5 + 3x – 4x + 2x2 (Rearranging terms and collecting the like terms together)
= 9 – x + 2x2 …………………(1)
Then we add (3x2 – 5x) and (–x2 + 2x + 5):
(3x2 – 5x) + (–x2 + 2x + 5)
= 3x2 – 5x – x2 + 2x + 5 (Taking care of the signs while opening the bracket)
= 3x2 – x2 – 5x + 2x + 5 (Rearranging terms and collecting the like terms together)
= 2x2 – 3x + 5 …………………(2)
Now we subtract (1) and (2):
(9 – x + 2x2) – (2x2 – 3x + 5)
= 9 – x + 2x2 – 2x2 + 3x – 5 (Taking care of the signs while opening the bracket)
= 9 – 5 – x + 3x + 2x2 – 2x2
= 4 + 2x (This is the result)
Exercise 12.4 Page No 246 (Old Textbook):
1. Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
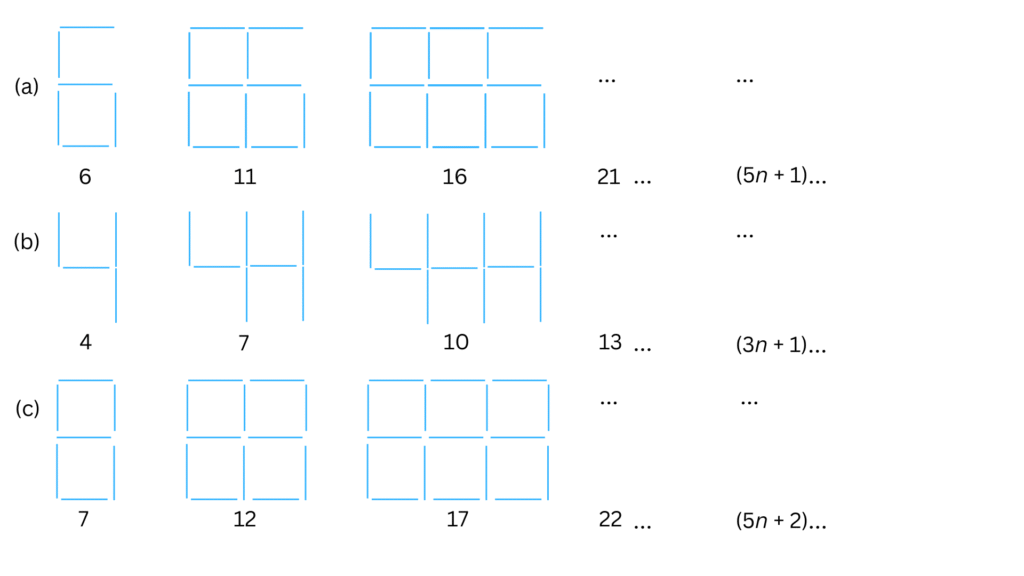
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern. How many segments are required to form 5, 10, 100 digits of the kind:
Answer:
(a) It is given that (5n + 1) segments are required to form n digits of the kind:

Therefore, to find how many segments are required to form 5 digits of that kind we substitute n = 5 in the expression (5n + 1):
5n + 1 = 5 × (5) + 1 = 25 + 1 = 26
So the number of segments are required to form 5 digits of that kind = 26.
To find how many segments are required to form 10 digits of that kind we substitute n = 10 in the expression (5n + 1):
5n + 1 = 5 × (10) + 1 = 50 + 1 = 51
So the number of segments are required to form 10 digits of that kind = 51.
To find how many segments are required to form 100 digits of that kind we substitute n = 100 in the expression (5n + 1):
5n + 1 = 5 × (100) + 1 = 500 + 1 = 501
So the number of segments are required to form 100 digits of that kind = 501.
(b) It is given that (3n + 1) segments are required to form n digits of the kind:

Therefore, to find how many segments are required to form 5 digits of that kind we substitute n = 5 in the expression (3n + 1):
3n + 1 = 3 × (5) + 1 = 15 + 1 = 16
So the number of segments are required to form 5 digits of that kind = 16.
To find how many segments are required to form 10 digits of that kind we substitute n = 10 in the expression (3n + 1):
3n + 1 = 3 × (10) + 1 = 30 + 1 = 31
So the number of segments are required to form 10 digits of that kind = 31.
To find how many segments are required to form 100 digits of that kind we substitute n = 100 in the expression (3n + 1):
3n + 1 = 3 × (100) + 1 = 300 + 1 = 301
(c) It is given that (5n + 2) segments are required to form n digits of the kind:

Therefore, to find how many segments are required to form 5 digits of that kind we substitute n = 5 in the expression (5n + 2):
5n + 2 = 5 × (5) + 2 = 25 + 2 = 27
So the number of segments are required to form 5 digits of that kind = 27.
To find how many segments are required to form 10 digits of that kind we substitute n = 10 in the expression (5n + 2):
5n + 2 = 5 × (10) + 2 = 50 + 2 = 52
So the number of segments are required to form 5 digits of that kind = 52.
To find how many segments are required to form 100 digits of that kind we substitute n = 100 in the expression (5n + 2):
5n + 2 = 5 × (100) + 2 = 500 + 2 = 502 So the number of segments are required to form 5 digits of that kind = 502.
2. Use the given algebraic expression to complete the table of number patterns.
| S. No | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | – | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | – | – | – | – | – | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | – | – | – | – | – | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | – | – | – | – | – | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | – | – | – | – | 10,001 | – |
Answer:
(i) For (2n – 1) the 100th term is obtained by substituting n = 100:
2n – 1 = 2 × (100) – 1 = 200 – 1 = 199
(ii) For (3n + 2) the 5th term is obtained by substituting n = 5:
3n + 2 = 3 × (5) + 2 = 15 + 2 = 17
For (3n + 2) the 10th term is obtained by substituting n = 10:
3n + 2 = 3 × (10) + 2 = 30 + 2 = 32
For (3n + 2) the 100th term is obtained by substituting n = 100:
3n + 2 = 3 × (100) + 2 = 300 + 2 = 302
(iii) For (4n + 1) the 5th term is obtained by substituting n = 5:
4n + 1 = 4 × (5) + 1 = 20 + 1 = 21
For (4n + 1) the 10th term is obtained by substituting n = 10:
4n + 1 = 4 × (10) + 1 = 40 + 1 = 41
For (4n + 1) the 100th term is obtained by substituting n = 100:
4n + 1 = 4 × (100) + 1 = 400 + 1 = 401
(iv) For (7n + 20) the 5th term is obtained by substituting n = 5:
7n + 20 = 7 × (5) + 20 = 35 + 20 = 55
For (7n + 20) the 10th term is obtained by substituting n = 10:
7n + 20 = 7 × (10) + 20 = 70 + 20 = 90
For (7n + 20) the 100th term is obtained by substituting n = 100:
7n + 20 = 7 × (100) + 20 = 700 + 20 = 720
(iv) For (n2 + 1) the 5th term is obtained by substituting n = 5:
n2 + 1 = (5)2 + 1 = 25 + 1 = 26
For (n2 + 1) the 10th term is obtained by substituting n = 10:
n2 + 1 = (10)2 + 1 = 100 + 1 = 101
The completed table is shown below:
| S. No | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | 199 | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | 17 | – | 32 | – | 302 | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | 21 | – | 41 | – | 401 | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | 55 | – | 90 | – | 720 | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | 26 | – | 101 | – | 10,001 | – |
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 10 Algebraic Expressions:
Very Short Answer Type Questions:
1. The expression 7x + 7x is a monomial or a binomial?
Answer:
7x + 7x = 14x and so it is a monomial expression.
2. How many terms does the expression x + y + z + 1 contain?
Answer:
The expression x + y + z + 1 contains 4 terms.
3. What is the coefficient of x2?
Answer:
The coefficient of x2 is 1.
4. How many terms does x – 1 + y – 1 have?
Answer:
x – 1 + y – 1 = x + y – 2, which has 3 terms.
5. Are (x – 5) and (5 – x) the same expression?
Answer:
No, they are different expressions which add to 0.
6. Expression (3x2 + 3xy) is subtracted twice from itself. What is the result?
Answer:
(3x2 + 3xy) – (3x2 + 3xy) – (3x2 + 3xy)
= 3x2 – 3x2 – 3x2 + 3xy – 3xy – 3xy
= -3x2 – 3xy
= -(3x2 + 3xy) which is negative of the expressions itself.
7. Write 5 factors of 3x2y?
Answer:
5 factors are: 3, x, x2, y, 3x.
8. List the factors of -y2.
Answer:
The factors are -1, y, -y, y2, -y2.
9. What is the coefficient of x in the expression 3x2y2 + 3y – 3xy2?
Answer:
The coefficient ofx is -3y2.
10. Find the value of (xy2 – x2y) for x = 2, y = 0?
Answer:
Putting x = 2, y = 0 in (xy2 – x2y) we get,
xy2 – x2y = 2(0)2 – 22(0) = 0 – 0 = 0 (Answer)
Multiple Choice Questions (MCQ):
1. A square has side of length x. If the area is added to the perimeter then the expression is:
(a) Monomial
(b) Binomial
(c) Trinomial
(d) Constant
Answer: (b) Binomial
Area of square = x2 and perimeter = 4x.
Hence (x2 + 4x) is a binomial expression.
2. If x is added to itself 10 times, the resulting expression will be:
(a) Monomial
(b) Trinomial
(c) Polynomial
(d) Constant
Answer: (a) Monomial
x + x + x + ….. + x = 10x. This is a monomial.
3. 5x/2 is a proper fraction for what value of x?
(a) 1/2
(b) 1/3
(c) 2
(d) 1
Answer:
We observe that 5x/2 = 5/2 × 1/3 = 5/6 .
4. Which term should be added to the expression (2xyz2 + 2x2y2z2 + 2xy2) to obtain an expression with four terms?
(a) – 3xy2
(b) x2y
(c) 6xyz2
(d) 3x2y2z2
Answer: (b) x2y
The expression (2xyz2 + 2x2y2z2 + 2xy2 + x2y) has 4 terms.
5. Expressions A and B both have 3 terms each. The first term in Expression A and the second term in Expression B are like terms. How many terms will we have if we add the expressions together?
(a) 6
(b) 5
(c) 4
(d) 3
Answer: (b) 5
The first term in Expression A and the second term in Expression B are like terms and when they are added they form a single term. There are 4 other unlike terms in the sum. Hence, there are (4 + 1) = 5 terms in the sum.
Short and Long Answer Type Questions:
1. What expression should be added to 3xy2 – 4xy to get 0?
Answer:
Let the required expression be A.
We get:
A + (3xy2 – 4xy) = 0
or, A + 3xy2 – 4xy – 3xy2 + 4xy = 0 – 3xy2 + 4xy [Adding -3xy2 and +4xy to both sides]
or, A + 0 = -3xy2 + 4xy
or, A = -3xy2 + 4xy (Answer)
2. What should we get if we add 3x2y3z + 4xy2z2 + 5x2y2z three times?
Answer:
(3x2y3z + 4xy2z2 + 5x2y2z) + (3x2y3z + 4xy2z2 + 5x2y2z) + (3x2y3z + 4xy2z2 + 5x2y2z)
= 3x2y3z + 3x2y3z + 3x2y3z + 4xy2z2 + 4xy2z2 + 5x2y2z + 5x2y2z + 5x2y2z (Rearranging terms)
= (3 + 3 + 3)x2y3z + (4 + 4 + 4)xy2z2 + (5 + 5 + 5)x2y2z (Using distributive law)
= 9x2y3z + 12xy2z2 + 15x2y2z (Answer)
3. What will be the coefficients be when we add the terms ax2, bx and cx2 together?
Answer:
ax2 + bx + cx2
= ax2 + cx2 + bx (Rearranging terms)
= (a + c)x2 + bx (Using distributive law)
The coefficient of x2 will be (a + c) and the coefficient of x will be b.
4. Add together:
(i) 2x – y – z, 2y – x – z, 2z – y – x (ii) x + y – z, z + x – y, y + z – x
Answers:
(i) 2x – y – z, 2y – x – z, 2z – y – x
Adding we get:
2x – y – z + 2y – x – z + 2z – y – x
= 2x – x – x – y + 2y – y – z – z + 2z (Rearranging terms)
= (2 – 1 – 1)x + (-1 + 2 – 1)y + (-1 – 1 + 2)z (Using distributive law)
= (0)x + (0)y + (0)z
= 0 + 0 + 0
= 0 (Answer)
(ii) x + y – z, z + x – y, y + z – x
Adding we get:
x + y – z + z + x – y + y + z – x
= x + x – x + y – y + y – z + z + z (Rearranging terms)
= (1 + 1 – 1)x + (1 – 1 + 1)y + (-1 + 1 + 1)z (Using distributive law)
= (1)x + (1)y + (1)z
= x + y + z (Answer)
5. The number of red balls is x, the number of blue balls is y and the number of green balls is z. It is given that four times the number of green balls is greater than three times the number of red balls and four times the number of blue balls combined. By how much is four times the number of green balls greater?
Answer:
Four times the number of green balls = 4z.
Three times the number of red balls = 3x.
Four times the number of blue balls = 4y.
Four times the number of green balls greater by 4z – (3x + 4y) or 4x – 3x – 4y.
6. There are (5x2 + 5xy) blue balls and (3y2 + 6xy) green balls in the bag. Out of these (2x2 + 5y) blue balls and (3y2 + 6y) green balls are removed. What are the remaining number of balls in the bag?
Answer:
Initially total number of balls
= (5x2 + 5xy) + (3y2 + 6xy)
= 5x2 + 3y2 + 5xy + 6xy (Rearranging terms)
= 5x2 + 3y2 + (5 + 6)xy (Using distributive law)
= 5x2 + 3y2 + 11xy
Total number of balls that are removed
= (2x2 + 5y) + (3y2 + 6y)
= 2x2 + 3y2 + 5y + 6y (Rearranging terms)
= 2x2 + 3y2 + (5 + 6)y (Using distributive law)
= 2x2 + 3y2 + 11y
The remaining number of balls in the bag
= (5x2 + 3y2 + 11xy) – (2x2 + 3y2 + 11y)
= 5x2 + 3y2 + 11xy – 2x2 – 3y2 – 11y
= 5x2 – 2x2 + 3y2 – 3y2 + 11xy – 11y (Rearranging terms)
= (5 – 2)x2 + (3 – 3)y2 + 11xy – 11y (Using distributive law)
= 3x2 + (0)y2 + 11xy – 11y = 3x2 + 11xy – 11y (Answer)
7. x2 + 2abxy + y2 equals to 1 for x = 2 and y = 3. What is the value of ab?
Answer:
Putting x = 2 and y = 3 we get,
22 + 2ab(2)(3) + 32 = 1
or, 4 + 12ab + 9 = 1
or, 12ab + 13 = 1
or, 12ab = 1 – 13
or, 12ab = -12
or, ab = -12/12
or, ab = -1 (Answer)
8. A certain type of bacteria is multiplying. The number of bacterial colonies formed in t hours is (t3 + t2 + 1). Find the number of bacterial colonies in t = 4 hours.
Answer:
In t hours the number of bacterial colonies formed is (t3 + t2 + 1).
In 4 hours the number of bacterial colonies formed is (4)3 + (4)2 + 1 = 64 + 16 + 1 = 81.
9. You are given the expressions (2xy2 + 2xy) where x and y can be any integer. Can you say whether the value of the expression is always even or always odd or depends on the specific values of x and y?
Answer:
Each term of the expression (2xy2 + 2xy) contains the even number 2 in it. When an even number is multiplied by other even or odd integers, the result is always even. Two even numbers added together gives another even number.
Let us take x = 2, y = 3.
We get:
2xy2 + 2xy = 2 × 2 × 32 + 2 × 2 × 2 = 36 + 8 = 44
Let us take x = 2, y = 4.
2xy2 + 2xy = 2 × 2 × 42 + 2 × 2 × 4 = 64 + 16 = 80
As you can see the value of the expression (2xy2 + 2xy) is always even for all values of x and y.
10. Anisa’s present age be y years. Anisa’s father’s age is 5 times Anisa’s age. Anisa’s grandfather’s age is 5 years more than the sum of Anisa’s age and Anisa’s father’s age. What is the difference between Anisa’s grandfather’s age and Anisa’s age?
Answer:
Anisa’s present age be y years.
Her father’s age = 5y.
The sum of Anisa’s age and Anisa’s father’s age = y + 5y = 6y.
Anisa’s grandfather’s age = 6y + 5.
Therefore, difference between Anisa’s grandfather’s age and Anisa’s age = (6y + 5 – y) = (5y + 5) years.
Fill in the Blanks:
(a) A constant term has no _________.
(b) The terms 5ab and -5ab are _________ terms.
(c) Like terms have same __________ factors.
(d) The integer 0 is a _________.
(e) The expression (n2 – 1) is _________ than (n2 + 1).
Answers:
(a) A constant term has no variable.
(b) The terms 5ab and -5ab are like terms.
(c) Like terms have same algebraic factors.
(d) The integer 0 is a monomial.
(e) The expression (n2 – 1) is less than (n2 + 1).
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 10 Algebraic Expressions:
An expert team of Indian and foreign educated engineers and scientists have designed these solutions and extra material to explain to you all the different concepts of algebraic expressions and how to solve related problems. We have included concise and coherent explanations wherever possible to help beginners easily grasp the concepts. If you study the solutions in detail your understanding of the material will definitely improve.
You can download free versions of the solutions anytime! We will keep providing you with top-quality study material and are always coming up with new ways to help you out. So make sure you keep visiting our website and join our email list to take advantage of the help we provide!
The main topics covered are:
10.1 – Introduction
10.2 – How are Expressions Formed?
10.3 – Terms of an Expression
10.4 – Like and Unlike Terms
10.5 – Monomials, Binomials, Trinomials and Polynomials
10.6 – Finding the Value of an Expression
Here are the number of problems by each chapter:
Exercise 10.1 – 7 questions
Exercise 10.2 – 10 questions
The vital part of this chapter is to study and understand the terms and definitions carefully. We put stress on this simple fact because these terms and definitions can seem confusing to beginners. Once you understand them perfectly, the next step will be to practise a variety of problems.
Need us to teach you? Need more practice? Our expert teacher-mentors will not only coach you but also mentor you regarding your future career at no extra cost. Contact us anytime with your requirements and we’ll be happy to help you out!
At educationroundtheworld.com we follow a teacher-mentor approach. In addition to top-quality teaching, we also mentor students regarding their future academic and professional careers. This helps a student realise their true talents and make educated choices about their future. We provide on-demand one-to-one coaching and mentoring, based on your convenience and your needs – have it completely your way! Reach out with your requirements and let us help you out! Book live classes now!


