Welcome students to an amazing chapter on exponents! We have prepared these solutions using scientific methods to make them interesting and to ensure that you get the maximum benefit from them. The extra material contains typical problems which will give you additional practice. Feel free to go through them in detail – we are confident they will be of good use to you.
Solutions to Exercise 11.1 (Page No 173) of NCERT Class 7 Math Chapter 11 Exponents and Powers –
1. Find the value of:
(i) 26
Answer: We can write:
26 = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 93
Answer: We can write:
93 = 9 × 9 × 9 = 729
(iii) 112
Answer: We can write:
112 = 11 × 11 = 121
(iv) 54
Answer: We can write:
54 = 5 × 5 × 5 × 5 = 625
2. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
Answer: The above can be written in the exponential form as 64.
(ii) t × t
Answer: The above can be written in the exponential form as t2.
(iii) b × b × b × b
Answer: The above can be written in the exponential form as b4
(iv) 5 × 5 × 7 × 7 × 7
Answer: The above can be written in the exponential form as 52 × 73.
(v) 2 × 2 × a × a
Answer: The above can be written in the exponential form as 22 × a2.
(vi) a × a × a × c × c × c × c × d
Answer: The above can be written in the exponential form as a3 × c4 × d.
3. Express each of the following numbers using the exponential notation:
(i) 512
Answer: As shown in the factorisation below, we have 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
So we can say that 512 = 29.

(ii) 343
Answer: As shown in the factorisation below, we have 343 = 7 × 7 × 7
So we can say that 343 = 73.

(iii) 729
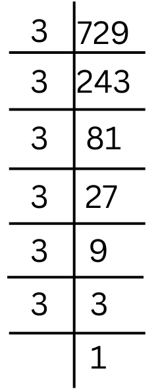
Answer: As shown in the factorisation below, we have 729 = 3 × 3 × 3 × 3 × 3 × 3
So we can say that 729 = 36
(iv) 3125
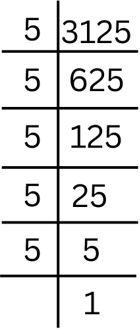
Answer: As shown in the factorisation below, we have 3125 = 5 × 5 × 5 × 5 × 5.
So we can say that 3125 = 55.
4. Identify the greater number, wherever possible, in each of the following.
(i) 43 or 34
Answer:
We know 43 = 4 × 4 × 4 = 64
and 34 = 3 × 3 × 3 × 3 = 81
Since 81 > 64, we can say 34 > 43.
Therefore, 34 is the greater number.
(ii) 53 or 35
Answer:
We know 53 = 5 × 5 × 5 = 125
and 35 = 3 × 3 × 3 × 3 × 3 = 243
Since 243 > 125, we can say 35 > 53.
Therefore, 35 is the greater number.
(iii) 28 or 82
Answer:
We know 28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
and 82 = 8 × 8 = 64
Since 256 > 64, we can say 28 > 82.
Therefore, 28 is the greater number.
(iv) 1002 or 2100
Answer:
We know 1002 = 100 × 100 = 10000
We can estimate if the value of 2100 is greater than 10000 by multiplying 2 by itself until we get a number greater 10000.
The expansion of 2100 is too big to evaluate easily. Therefore, we choose simplify the task.
We think of a big enough power which is less than 100, to see whether the resulting number will be > 10000.
We choose 210.
We evaluate 210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024 which is < 10000.
Then we choose 213 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 8192 which we can see is still < 10000 but is close.
So we decide to choose 214 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 16384 which is > 10000.
Therefore, we conclude that 214 > 10000 or 214 > 1002, so 2100 (which is much greater than 214) is obviously greater than 1002.
Therefore, 2100 is the greater number.
(v) 210 or 102
Answer:
We know 210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
and 102 = 10 × 10 = 100
Since 1024 > 100, we can say 210 > 102.
Therefore, 210 is the greater number.
5. Express each of the following as a product of powers of their prime factors:
(i) 648
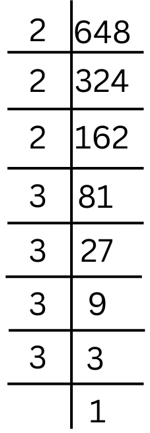
Answer: We observe that 648
= 2 × 324
= 2 × 2 × 162
= 2 × 2 × 2 × 81
= 2 × 2 × 2 × 3 × 27
= 2 × 2 × 2 × 3 × 3 × 9
= 2 × 2 × 2 × 3 × 3 × 3 × 3
= 23 × 34
The prime factorisation is shown below:
(ii) 405
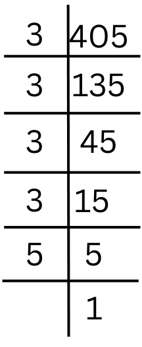
Answer: We observe that 405
= 3 × 135
= 3 × 3 × 45
= 3 × 3 × 3 × 15
= 3 × 3 × 3 × 3 × 5
= 34 × 5
The prime factorisation is shown below:
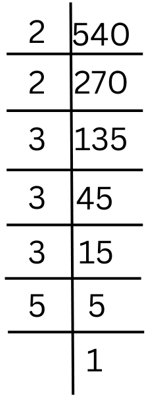
(iii) 540
Answer: We observe that 540
= 2 × 270
= 2 × 2 × 135
= 2 × 2 × 3 × 45
= 2 × 2 × 3 × 3 × 15
= 2 × 2 × 3 × 3 × 3 × 5
= 22 × 33 × 5
The prime factorisation is shown below:
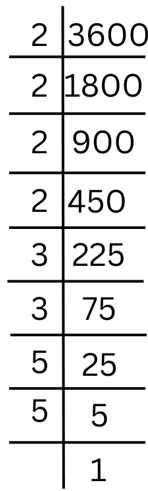
(iv) 3600
Answer: We observe that 3600
= 2 × 1800
= 2 × 2 × 900
= 2 × 2 × 2 × 450
= 2 × 2 × 2 × 2 × 225
= 2 × 2 × 2 × 2 × 3 × 75
= 2 × 2 × 2 × 2 × 3 × 3 × 25
= 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 24 × 32 × 52
The prime factorisation is shown below:
6. Simplify:
(i) 2 × 103
Answer:
2 × 103 = 2 × 10 × 10 × 10 = 2 × 1000 = 2000
(ii) 72 × 22
Answer:
72 × 22 = 7 × 7 × 2 × 2 = 49 × 4 = 196
(iii) 23 × 5
Answer:
23 × 5 = 2 × 2 × 2 × 5 = 8 × 5 = 40
(iv) 3 × 44
Answer:
3 × 44 = 3 × 4 × 4 × 4 × 4 = 768
(v) 0 × 102
Answer:
0 × 102 = 0 × 100 = 0
(vi) 52 × 33
Answer:
52 × 33 = 5 × 5 × 3 × 3 × 3 = 675
(vii) 24 × 32
Answer:
24 × 32 = 2 × 2 × 2 × 2 × 3 × 3 = 144
(viii) 32 × 104
Answer:
32 × 104 = 3 × 3 × 10 × 10 × 10 × 10 = 9 × 10000 = 90000
7. Simplify:
(i) (– 4)3
Answer:
(– 4)3 = (– 4) × (– 4) × (– 4) = (16) × (– 4) = – 64
Note how the negative base raised to the odd power gives a negative result.
(ii) (–3) × (–2)3
Answer:
(–3) × (–2)3
= (–3) × (– 2) × (– 2) × (– 2)
= (–3) × (– 8) [ Note how the negative base (– 2) raised to the odd power 3 gives a negative result]
= 24
(iii) (–3)2 × (–5)2
Answer:
(–3)2 × (–5)2
= (–3) × (–3) × (–5) × (–5)
= (9) × (25) [ Note how the negative bases (–3) and (–5) raised to the even power 2 gives a positive result)
= 225
(iv) (–2)3 × (–10)3
Answer:
(–2)3 × (–10)3
= (–2) × (–2) × (–2) × (–10) × (–10) × (–10)
= (–8) × (–1000) [ Note how the negative bases (–2) and (–10) raised to the odd power 3 gives a negative result)
= 8000
8. Compare the following numbers:
(i) 2.7 × 1012 ; 1.5 × 108
Answer:
In both the numbers the base is 10. In case of 2.7 × 1012 the exponent is 12 and in case of 1.5 × 108 the exponent is 8.
Since 12 > 8, we get 1012 > 108 and therefore we can say that 2.7 × 1012 > 1.5 × 108.
(ii) 4 × 1014 ; 3 × 1017
Answer:
In both the numbers the base is 10. In case of 4 × 1014 the exponent is 14 and in case of 3 × 1017the exponent is 17.
Since 14 < 17, we get 1014 < 1017 and therefore we can say that 4 × 1014 < 3 × 1017.
Solutions to Exercise 11.2 (Page No 181) of NCERT Class 7 Math Chapter 11 Exponents and Powers –
1. Using laws of exponents, simplify and write the answer in exponential form:
(i) 32 × 34 × 38
Answer:
We know that for any non-zero integer a, where m and n are whole numbers:
am × an = am + n
Therefore, we can simply say that when we multiply numbers with the same base with different powers, the base remains the same and the powers get added in the product.
So,
32 × 34 × 38 = 32 + 4 + 8 = 314
(ii) 615 ÷ 610
Answer:
We know that for any non-zero integer a, where m and n are whole numbers and m > n:
am ÷ an = am – n
Therefore, we can simply say that when we divide numbers with the same base with different powers, the base remains the same and the powers get subtracted in the product.
So,
615 ÷ 610 = (6)15 – 10 = 65
(iii) a3 × a2
Answer:
We know that for any non-zero integer a, where m and n are whole numbers:
am × an = am + n
Therefore, we can simply say that when we multiply numbers with the same base with different powers, the base remains the same and the powers get added in the product.
So,
a3 × a2 = (a)3 + 2 = a5
(iv) 7x × 72
Answer:
We know that for any non-zero integer a, where m and n are whole numbers:
am × an = am + n
Therefore, we can simply say that when we multiply numbers with the same base with different powers, the base remains the same and the powers get added in the product.
So,
7x × 72 = (7)x + 2
(v) (52)3 ÷ 53
Answer:
We know that for any non-zero integer a, where m and n are whole numbers:
(am)n = amn
So,
(52)3 = 53 × 2 = 56
So,
(52)3 ÷ 53 = 56 ÷ 53
We know that for any non-zero integer a, where m and n are whole numbers and m > n:
am ÷ an = am – n
Therefore, we can simply say that when we divide numbers with the same base with different powers, the base remains the same and the powers get subtracted in the product.
So,
56 ÷ 53 = (5)6 – 3 = 53
(vi) 25 × 55
Answer:
We know that for any non-zero integers a and b, where m is any whole number:
am × bm = (ab)m
Therefore, we can simply say that when we multiply numbers with different bases, but same exponents the bases get multiplied and the power remains the same.
So,
25 × 55 = (2 × 5)5 = 105
(vii) a4 × b4
Answer:
We know that for any non-zero integers a and b, where m is any whole number:
am × bm = (ab)m
Therefore, we can simply say that when we multiply numbers with different bases, but same exponents the bases get multiplied and the power remains the same.
So,
a4 × b4 = (ab)4
(viii) (34)3
Answer:
We know that for any non-zero integer a, where m and n are whole numbers:
(am)n = amn
So,
(34)3 = 34 × 3 = 312
(ix) (220 ÷ 215) × 23
Answer:
We know that for any non-zero integer a, where m and n are whole numbers and m > n:
am ÷ an = am – n
Therefore, we can simply say that when we divide numbers with the same base with different powers, the base remains the same and the powers get subtracted in the product.
So,
(220 ÷ 215) = (2)20 – 15 = 25
Therefore,
(220 ÷ 215) × 23
= 25 × 23
We know that for any non-zero integer a, where m and n are whole numbers:
am × an = am + n
So,
25 × 23 = (2)5 + 3 = 28
(x) 8t ÷ 82
Answer:
We know that for any non-zero integer a, where m and n are whole numbers and m > n:
am ÷ an = am – n
Therefore, we can simply say that when we divide numbers with the same base with different powers, the base remains the same and the powers get subtracted in the product.
So,8t ÷ 82 = (8)t – 2
2. Simplify and express each of the following in exponential form:
(i) (23 × 34 × 4)/(3 × 32)
Answer:
(23 × 34 × 4)/(3 × 32)
= (23 × 34 × 4)/(3 × 25)
= (23 × 22 × 34)/(25 × 3)
= (23 + 2 × 34)/(25 × 3) (Adding the power of 2 in the numerator during multiplication: am × an = am + n)
= (25 × 34)/(25 × 3)
= 25 – 5 × 34 – 1 (Subtracting the powers of 2 and 3 during division: am ÷ an = am – n)
= 20 × 33
= 1 × 27 (Since a0 = 1 for any non-zero integer a)
= 27
(ii) ((52)3 × 54) ÷ 57
Answer:
((52)3 × 54) ÷ 57
= ((5)2 × 3 × 54) ÷ 57 (Since for any non-zero integer a, (am)n = amn)
= (56 × 54) ÷ 57
= 5(6 + 4) ÷ 57 (Adding the power of 5 during multiplication: am × an = am + n)
= 510 ÷ 57
= 510 – 7 (Subtracting the power of 5 during division: am ÷ an = am – n)
= 53
(iii) 254 ÷ 53
Answer:
254 ÷ 53
= (52)4 ÷ 53
= (5)2 × 4 ÷ 53 (Since for any non-zero integer a, (am)n = amn)
= 58 ÷ 53
= 55 (Subtracting the powers of 5 during division: am ÷ an = am – n)
(iv) (3 × 72 × 118)/(21 × 113)
Answer:
(3 × 72 × 118)/(21 × 113)
= (3 × 72 × 118)/(3 × 7 × 113 ) (Writing 21 = 3 × 7)
= 31 – 1 × 72 – 1 × 118 – 3 (Subtracting the powers of 3, 7, 11 during division: am ÷ an = am – n)
= 30 × 71 × 115
= 1 × 7 × 115 (Since a0 = 1 for any non-zero integer a)
= 7 × 115
(v) 37/(34 × 33)
Answer:
37/(34 × 33)
= 37/34 + 3 (Adding the powers of 3 during multiplication: am × an = am + n)
= 37/37
= 30 (Subtracting the power of 3 during division: am ÷ an = am – n)
= 1 (Since a0 = 1 for any non-zero integer a)
(vi) 20 + 30 + 40
Answer:
20 + 30 + 40
= 1 + 1 + 1 (Since a0 = 1 for any non-zero integer a)
= 3
(vii) 20 × 30 × 40
Answer:
20 × 30 × 40
= 1 × 1 × 1 (Since a0 = 1 for any non-zero integer a)
= 1
(viii) (30 + 20) × 50
Answer:
(30 + 20) × 50
= (1 + 1) × 1 (Since a0 = 1 for any non-zero integer a)
= 2 × 1
= 2
(ix) (28 × a5)/(43 × a3)
Answer:
(28 × a5)/(43 × a3)
= (28 × a5)/(22)3 × a3 ) (Since 4 = 22)
= (28 × a5)/(22×3 × a3 ) (Since for any non-zero integer a, (am)n = amn)
= (28 × a5)/(26 × a3 )
= 28 – 6 × a5 – 3 (Subtracting the powers of 2 and a during division: am ÷ an = am – n)
= 22 × a2
= (2a)2 (Since am × bm = (ab)m)
(x) (a5/a3) × a8
Answer:
(a5/a3 ) × a8
= a(5 – 3) × a8 (Since am ÷ an = am – n)
= a2 × a8
= a2 + 8 (Since am × an = am + n)
= a10
(xi) (45 × a8 b3)/(45 × a5b2)
Answer:
(45 × a8 b3)/(45 × a5b2)
(45 × a8 × b3)/(45 × a5 × b2)
= 45 – 5 × a8 – 5 × b3 – 2
= 40 × a3 × b1 (Subtracting the powers of 4, a, b during division: am ÷ an = am – n)
= 1 × a3 × b (Since a0 = 1 for any non-zero integer a)
= a3b
(xii) (23 × 2)2
Answer:
(23 × 2)2
= (23 + 1)2 (Since am × an = am + n)
= (24)2
= 24 × 2 (Since for any non-zero integer a, (am)n = amn)
= 28
3. Say true or false and justify your answer:
(i) 10 × 1011 = 10011
Answer:
Let us take the LHS:
10 × 1011
= 101 × 1011
= 101 + 11 (Since am × an = am + n)
= 1012
Now let us take the RHS:
10011
= (10 × 10)11
= 1011 × 1011 (Since we know am × bm = (ab)m, the reverse (ab)m = am × bm)
= 1011 + 11
= 1022
Since 1022 > 1011 we can say that RHS ≠ LHS. Therefore, the given statement is False.
(ii) 23 > 52
Answer:
Let us take the LHS:
23 = 2 × 2 × 2 = 8
Let us take the RHS:
52 = 5 × 5 = 25
Since 8 < 25, we can say that RHS ≠ LHS. Therefore, the given statement is False.
(iii) 23 × 32 = 65
Answer:
Let us take the LHS:
23 × 32 = 2 × 2 × 2 × 3 × 3 = 72
Let us take the RHS:
65 = 6 × 6 × 6 × 6 × 6 = 7776
Since 72 < 7776, we can say that RHS ≠ LHS. Therefore, the given statement is False.
(iv) 30 = (1000)0
Answer:
Let us take the LHS:
30 = 1 (Since a0 = 1 for any non-zero integer a)
Let us take the RHS:
(1000)0 = 1 (Since a0 = 1 for any non-zero integer a)
Since LHS = RHS, the given statement is True.
4. Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
Answer:
Breaking down 108 and 192 into prime factors we get:
108 × 192
= (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (22 × 33) × (26 × 3)
= 22 × 26 × 33 × 3
= 22 + 6 × 33 + 1
= 28 × 34
(ii) 270
Answer:
Breaking down 270 into prime factors we get:
270
= 2 × 3 × 3 × 3 × 5
= 2 × 33 × 5
(iii) 729 × 64
Answer:
Breaking down 729 and 64 into prime factors we get:
729 = 3 × 3 × 3 × 3 × 3 × 3 = 36
64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
Therefore,
729 × 64 = 36 × 26
(iv) 768
Answer:
Breaking down 768 into prime factors we get:
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 28 × 3
5. Simplify
(i) (25)2 × 73)/(83 × 7)
Answer:
(25)2 × 73)/(83 × 7)
= (25)2 × 73)/((23)3 × 7) (Writing 8 = 23)
= (25 × 2 × 73)/(23 × 3 × 7) (Since for any non-zero integer a, (am)n = amn)
= (210 × 73)/(29 × 7)
= 210 – 9 × 73 – 1
= 21 × 72 (Subtracting the powers of 2, 7 during division: am ÷ an = am – n)
= 2 × 49
= 98
(ii) (25 × 52 × t8)/(103 × t4)
Answer:
(25 × 52 × t8)/(103 × t4)
= (52 × 52 × t8)/((5 × 2)3 × t4) (Since 25 = 52 and 10 = 5 × 2)
= (52 + 2 × t8)/(53 × 23 × t4) (Since am × an = am + n and (ab)m = am × bm)
= (54 × t8)/(53 × 23 × t4)
= (54-3 × t8-4)/23 (Subtracting the powers of 5, t during division: am ÷ an = am – n)
= (51 × t4)/(2 × 2 × 2)
= 5t4/8
(iii) (35 × 105 × 25)/(57 × 65)
Answer:
(35 × 105 × 25)/(57 × 65)
= (35 × (2 × 5)5 × 52)/(57 × (2 × 3)5 ) (Putting 10 = 2 × 5 and 6 = 2 × 3)
= (35 × 25 × 55 × 52)/(57 × 25 × 35 ) (Since (ab)m = am × bm)
= (55 × 52 × 25 × 35 )/(57 × 25 × 35)
= (55 + 2 × 25 × 35)/(57 × 25 × 35) (Since am × an = am + n and (ab)m = am × bm)
= (57 × 25 × 35)/(57 × 25 × 35)
= 57 – 7 × 25 – 5 × 35 – 5
= 50 × 20 × 30
= 1 × 1 × 1 (Since a0 = 1 for any non-zero integer a)
= 1
Solutions to Exercise 11.3 (Page No 184) of NCERT Class 7 Math Chapter 11 Exponents and Powers –
1. Write the following numbers in the expanded forms:
(a) 279404
Answer:
We already know how to expand a number. Therefore, the expansion of 279404:
279404 = (2 × 100000) + (7 × 10000) + (9 × 1000) + (4 × 100) + (0 × 10) + (4 × 1)
We know, 100000 = 105, 10000 = 104, 1000 = 103, 100 = 102, 10 = 101, 1 = 100
Now let’s express it using powers of 10 in the exponent form:
279404 = (2 × 105) + (7 × 104) + (9 × 103) + (4 × 102) + (0 × 101) + (4 × 100)
(b) 3006194
Answer:
We already know how to expand a number. Therefore, the expansion of 3006194:
3006194 = (3 × 1000000) + (0 × 100000) + (0 × 10000) + (6 × 1000) + (1 × 100) + (9 × 10) + (4 × 1)
We know, 1000000 = 106, 100000 = 105, 10000 = 104, 1000 = 103, 100 = 102, 10 = 101, 1 = 100
Now let’s express it using powers of 10 in the exponent form:
3006194 = (3 × 106) + (0 × 105) + (0 × 104) + (6 × 103) + (1 × 102) + (9 × 101) + (4 × 100)
(c) 2806196
Answer:
We already know how to expand a number. Therefore, the expansion of 2806196:
2806196 = (2 × 1000000) + (8 × 100000) + (0 × 10000) + (6 × 1000) + (1 × 100) + (9 × 10) + (6 × 1)
We know, 1000000 = 106, 100000 = 105, 10000 = 104, 1000 = 103, 100 = 102, 10 = 101, 1 = 100
Now let’s express it using powers of 10 in the exponent form:
2806196 = (2 × 106) + (8 × 105) + (0 × 104) + (6 × 103) + (1 × 102) + (9 × 101) + (6 × 100)
(d) 120719
Answer:
We already know how to expand a number. Therefore, the expansion of 120719:
120719 = (1 × 100000) + (2 × 10000) + (0 × 1000) + (7 × 100) + (1 × 10) + (9 × 1)
We know, 100000 = 105, 10000 = 104, 1000 = 103, 100 = 102, 10 = 101, 1 = 100
Now let’s express it using powers of 10 in the exponent form:
120719 = (1 × 105) + (2 × 104) + (0 × 103) + (7 × 102) + (1 × 101) + (9 × 100)
(e) 20068
Answer:
We already know how to expand a number. Therefore, the expansion of 20068:
20068 = (2 × 10000) + (0 × 1000) + (0 × 100) + (6 × 10) + (8 × 1)
We know, 10000 = 104, 1000 = 103, 100 = 102, 10 = 101, 1 = 100
Now let’s express it using powers of 10 in the exponent form:
20068 = (2 × 104) + (0 × 103) + (0 × 102) + (6 × 101) + (8 × 100)
2. Find the number from each of the following expanded forms:
(a) 8 × 104 + 6 × 103 + 0 × 102 + 4 × 101 + 5 × 100
Answer:
8 × 104 + 6 × 103 + 0 × 102 + 4 × 101 + 5 × 100
= 8 × 10000 + 6 × 1000 + 0 × 100 + 4 × 10 + 5 × 1
= 80000 + 6000 + 0 + 40 + 5
= 86045
(b) 4 × 105 + 5 × 103 + 3 × 102 + 2 × 100
Answer:
4 × 105 + 5 × 103 + 3 × 102 + 2 × 100
= 4 × 100000 + 5 × 1000 + 3 × 100 + 2 × 1
= 400000 + 5000 + 300 + 2
= 405302
(c) 3 × 104 + 7 × 102 + 5 × 100
Answer:
3 × 104 + 7 × 102 + 5 × 100
= 3 × 10000 + 7 × 100 + 5 × 1
= 30000 + 700 + 5
= 30705
(d) 9 × 105 + 2 × 102 + 3 × 101
Answer:
9 × 105 + 2 × 102 + 3 × 101
= 9 × 100000 + 2 × 100 + 3 × 10
= 900000 + 200 + 30
= 900230
3. Express the following numbers in standard form:
(i) 5,00,00,000
Answer: The standard form of the number = 5 × 107.
(ii) 70,00,000
Answer: The standard form of the number = 7 × 106.
(iii) 3,18,65,00,000
Answer: The standard form of the number = 3.1865 × 109.
(iv) 3,90,878
Answer: The standard form of the number = 3.90878 × 105.
(v) 39087.8
Answer: The standard form of the number = 3.90878 × 104.
(vi) 3908.78
Answer: The standard form of the number = 3.90878 × 103.
4. Express the number appearing in the following statements in standard form.
(a) The distance between Earth and Moon is 384,000,000 m.
Answer: The standard form of the number = 3.84 × 108 m.
(b) Speed of light in a vacuum is 300,000,000 m/s.
Answer: The standard form of the number = 3 × 108 m/s.
(c) Diameter of the Earth is 1,27,56,000 m.
Answer: The standard form of the number = 1.2756 × 107 m.
(d) Diameter of the Sun is 1,400,000,000 m.
Answer: The standard form of the number = 1.4 × 109 m.
(e) In a galaxy, there are, on average, 100,000,000,000 stars.
Answer: The standard form of the number = 1 × 1011 stars.
(f) The universe is estimated to be about 12,000,000,000 years old.
Answer: The standard form of the number = 1.2 × 1010 years.
(g) The distance of the Sun from the centre of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000,000 m.
Answer: The standard form of the number = 3 × 1020 m.
(h) 60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8 gm.
Answer: The standard form of the number = 6.023 × 1022 molecules.
(i) The Earth has 1,353,000,000 cubic km of seawater.
Answer: The standard form of the number = 1.353 × 109 cubic km.
(j) The population of India was about 1,027,000,000 in March 2001.
Answer: The standard form of the number = 1.027 × 109.
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 11 Exponents and Powers:
Very Short Answer Type Questions:
1. What is the value of (2 × 3)0 ?
Answer:
(2 × 3)0 = 60 = 1.
2. What is the value of (1/t)0?
Answer:
The value of (1/t)0= 1.
3. How many 22‘s need to be multiplied together to get 64?
Answer:
We observe that: 22× 22 × 22 = 22 + 2 + 2 = 26 = 64.
Therefore, three 22’s should be multiplied together to get 64.
4. Find the value of 3-(-5).
Answer:
The value of3-(-5)= 35 = 243.
5. If 5x = 1, then what is the value of (x + 2)?
Answer:
5x = 1
or, 5x = 50
or, x = 0 or, x + 2 = 2 (Answer)
6. If 3x/3x-y = 3, what is the value of y?
Answer:
If 3x/3x-y = 3
or, 3x – x + y = 3
or, 3y = 31 or, y = 1 (Answer)
7. Express 54 as a product of prime factors.
Answer:
54 = 2 × 33 (Expressed as a product of prime factors)
8. Find the value of – (-4/3)3?
Answer:
– (-4/3)3
= – (-1)3 × (4)3/33
= 43/33
= 64/27 (Answer)
9. 5x + 1 + 5x = 6, where x is an integer. What is the value of x?
Answer:
We observe that for x = 0, 50 + 1 + 50 = 6. Therefore, the value of integer x = 0.
10. 3100 = x.398 then what is value of x?
Answer:
3100 = x.398
or, 32.398 = x.398
or, x = 32 = 9 (Answer)
Multiple Choice Questions (MCQ):
1. Find the value of: (p2 × p4 × t9)/(p6 × 32 × (-t)4 )
(a) t5/9
(b) – t5/9
(c) (pt)/9
(d) 1/9
Answer: (a) t5/9
(p2 × p4 × t9)/(p6 × 32 × (-t)4 )
= (p2 + 4 × t9)/(p6 × 32 × (-t)4 ) [ Using am × an = am + n ]
= (p6 × t9)/(p6 × 32 × (-t)4 )
= p6 – 6 × t9 – 4 × 1/32
= (p0 t5)/9
= t5/9 (Answer)
2. If 1/6n = 1/216 , what is the value of n?
(a) 3
(b) 1/3
(c) 4
(d) 2
Answer: (a) 3
1/6n = 1/216
or, 1/6n = 1/63
or, n = 3 (By comparison)
3. If xn = 1/(n2 + 1) , find the value of x3.
(a) 1/5
(b) 1/10
(c) 1/4
(d) 1/9
Answer: (b) 1/10
xn = 1/(n2 + 1)
or, x3 = 1/(32 + 1)
or, x3 = 1/10
4. If xmyn [(x6 × y2)/(xy)2] = x8y10, then find the value of m and n.
(a) m = 4, n= 4
(b) m = 4, n = 10
(c) m = 3, n = 10
(d) m = 4, n = 8
Answer: (b) m = 4, n = 10
xmyn [(x6 × y2)/(xy)2]
= xmyn [(x6 × y2)/(x2 × y2 )]
= xmyn × x6 – 2 × y2 – 2
= xmyn × x4 × y0
= xm × x4 × yn × 1
= xm + 4 × yn = x8y10
Comparing we get:
m + 4 = 8 and n = 10
Therefore, m = 4 and n = 10 (Answer)
5. The power of x2n + 1 where n is any integer is:
(a) Even
(b) Odd
(c) Can be even or odd depending on the value of n
(d) Is always positive
Answer: (b) Odd
If n is an integer then (2n + 1) is always odd.
Also, (2n + 1) can be positive or negative depending on the value of n. Therefore, (d) is not true.
Short Answer and Long Answer Type Questions:
1. Simplify and write the answer in exponential form:
(i) 2/3 × 3/2 × 2/3 × 2/3 (ii) t × (t/5)2× (1/t)2
Answers:
(i) 2/3 × 3/2 × 2/3 × 2/3
= 2/3 × 2/3 × 2/3 × 3/2
= (2 × 2 × 2 × 3)/(2 × 3 × 3 × 3)
= (2 × 2)/(3 × 3)
= 22/32
= (2/3)2(Answer)
(ii) t × (t/5)2× (1/t)2
= t × t2/52 × 12/t2
= (t × t2)/t2 × 1/52
= t3/t2 × 1/52
= t3 – 2 × 1/52
= t/52 (Answer)
2. Simplify and express each of the following in exponential form:
(i) 16 × (t/2)3 (ii) (25 × 36)/(42 × 33)
Answers:
(i) 16 × (t/2)3
= 24 × t3/23
= 24/23 × t3
= 24 – 3 × t3
= 2t3 (Answer)
(ii) (25 × 36)/(42 × 33)
= (25 × 36)/((22)2 × 33)
= (25 × 36)/(24 × 33)
= 25 – 4 × 36 – 3
= 2 × 33 (Answer)
3. Show that the following equivalent:
(i) 66m (ii) (26)m × (36)m (iii) (6m)2 × (6m)4
Answer:
(ii) (26)m × (36)m
= 26m × 36m
= (2 × 3)6m
= 66m
(iii) (6m)2 × (6m)4
= 62m × 64m
= 62m + 4m
= 66m
Hence it is proved that (i), (ii) and (iii) are equal.
4. Simplify using the laws of exponents:
(i) (54 × 25)/(50 × 27) (ii) (32 × 50 × 49)/(14 × 18 × 10)
Answer:
(i) (54 × 25)/(50 × 27)
= (2 × 33 × 52)/(2 × 52 × 33)
= 21 – 1 × 33 – 3 × 52 – 2
= 20 × 30 × 50
= 1 (Answer)
(ii) (32 × 50 × 49)/(14 × 18 × 10)
= (25 × 2 × 52 × 72)/(2 × 7 × 2 × 32 × 2 × 5)
= (26 × 52 × 72)/(23 × 7 × 32 × 5)
= 26 – 3 × 52 – 1 × 72 – 1 × 1/9
= 23 × 5 × 7 × 1/9
= 280/9 (Answer)
5. Answer the following:
(a) If 2nx + 3n + 1y = n + 2, find the value of (x + 3y)?
(b) If + y = (n + 1)2, find the value of (x + y)?
Answers:
(a)2nx + 3n + 1y = n + 2
Putting n = 0 we get,
20x + 30 + 1y = 0 + 2
or, x + 3y = 2 (Answer)
(b) x/n + y = (n + 1)2
Putting x = 1 we get,
x/1 + y = (1 + 1)2
or, x + y = 22
or, x + y = 4 (Answer)
6. If (2)x (3)y (7)z = 16 × 8 × 9 × 21, find the value of x, y, z.
Answer:
(2)x (3)y (7)z = 16 × 8 × 9 × 21
or, (2)x (3)y (7)z = 24 × 23 × 32 × 3 × 7
or, (2)x (3)y (7)z = 27 × 33 × 7
Comparing LHS with RHS we get, x = 7, y = 3 and z = 1.
7. If 1/(m4n2) = (3 × 5)/(27 × 9 × 125) where m and n are integers, find the value of m and n.
Answer:
1/(m4n2) = (3 × 5)/(27 × 9 × 125)
or, 1/(m4n2) = (3 × 5)/(35 × 53 )
or, 1/(m4n2) = (3 × 5)/(34 × 3 × 52 × 5)
or, 1/(m4n2) = 1/(34 × 52 )
Comparing LHS with RHS we get the integer m = 3 and the integer n = 5.
8. If a4 b2 = c2d4 then find the value of:
(a8 b4)/(c4 d8)
Answers:
(a8 b4)/(c4 d8)
a4 b2 = c2d4
or, (a4 × b2)2 = (c2 × d4)2 (Squaring both sides)
or, (a4)2 × (b2)2 = (c2)2 × (d4)2
or, a8 × b4 = c4 × d8
or, (a8 b4)/(c4 d8)
= 1 (Answer)
9. Simplify: (xa + b – c × ya – b + c)/(xa – b – c × y-a- b + c)
Answer:
(xa + b – c × ya – b + c)/(xa – b – c × y-a- b + c)
= x(a + b – c) – (a – b – c) × y(a – b + c) – (– a – b + c)
= xa + b – c – a + b + c × ya – b + c + a + b – c
= x2b × y2a (Answer)
10. Find:
Given: 3x + 3y + 3z = 9. Find the value of:
(i) 3x + 2 + 3y + 2 + 3z + 2 (ii) 3x – 1 + 3y – 1 + 3z – 1
Answers:
(i) 3x + 2 + 3y + 2 + 3z + 2
3x + 3y + 3z = 9
Multiplying both sides by 32 we get:
32(3x + 3y + 3z) = 9 × 32
or, 3x + 2 + 3y + 2 + 3z + 2 = 81 (Answer)
(ii) 3x – 1 + 3y – 1 + 3z – 1
3x + 3y + 3z = 9
Dividing both sides by 3 we get:
(3x + 3y + 3z)/3 = 9/3
or, 3x/3 + 3y/3 + 3z/3 = 3
or, 3x – 1 + 3y – 1 + 3z – 1 = 3 (Answer)
Fill in the Blanks:
(a) 38 is _________ than 83.
(b) 379920 expressed in standard form is __________.
(c) The value of 4 × 103 + 3 × 102 + 2 × 101 + 0 × 100 is __________.
(d) The value of (23+ 25)/2 is __________.
(e) The length of a rectangle is 24 cm and breadth is 12 cm. The area of the rectangle in terms of its prime factors is _________.
Answer:
(a) 38 is greater than 83.
(b) 379920 expressed in standard form is 3.79920 × 105.
(c) The value of 4 × 103 + 3 × 102 + 2 × 101 + 0 × 100 is 4320.
(d) The value of (23 + 25)/2 is 20.
(e) The length of a rectangle is 24 cm and breadth is 12 cm. The area of the rectangle in terms of its prime factors is 25 × 32.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 11 Exponents and Powers:
These solutions have been prepared by an expert team of Indian and foreign educated engineers and scientists following proven methods to ensure maximum learning and retention. Literally everything you need to know to be able to solve problems is included in the solutions. We are confident that if you study them in detail, you will benefit greatly from them.
We have included free PDFs of the solutions which you can download anytime! We will keep providing you with lots of useful study material, resources and other info. So make sure you keep visiting our website and join our email list to get free access to the opportunities we provide!
The main topics covered are:
11.1 – Introduction
11.2 – Exponents
11.3 – Laws of Exponents
11.4 – Miscellaneous Examples Using the Laws of Exponents
11.5 – Decimal Number System
11.6 – Expressing Large Numbers in the Standard Form
Here are the number of problems by each chapter:
Exercise 11.1 – 8 questions
Exercise 11.2 – 5 questions
Exercise 11.3 – 4 questions
It is vital that you understand the laws of exponents very well. Make sure you understand how the formulae and rules are derived. You might come across situations which require you to derive them from scratch yourself. Also, you might forget the rules or confuse yourself during an exam (don’t worry, its normal!), so you will be on the safe side if you know how to derive them.
For this chapter we recommend regular practice. The techniques in the chapter will require lots of practice to perfect. Practise many different kinds of problems until you feel confident using all the techniques. Concentrate on problems that require a combination of the laws of exponents to solve. You will definitely see problems of this type in your exams. Also keep practising regularly, so that you don’t forget the concepts.
Anytime you need additional help, our expert teacher-mentors will be there for you. Contact us with your requirements anytime and let us help you out! (insert hyperlink).
Our expert teacher-mentors at educationroundtheworld.com look forward to teaching bright young students like you and will go the extra mile to help you succeed. Top-quality coaching along with the right kind of mentoring regarding your future can work wonders. You will know of available opportunities and discover where your true talents lie. So, anytime you need extra help feel free to get in touch with us. We provide on-demand one-to-one coaching, based on your convenience and your needs – have it completely your way! Book any number of appointments now!


