Hello students! Looking for reliable solutions to Chapter 12 Symmetry? Here we’ve provided excellent solutions (along with amazing figures) to all the problems in this chapter. We have even included a set of extra problems and their solutions for you to practise. We recommend you go through them in detail – they should clear all your doubts and help you understand the concepts.
Solutions to Exercise 12.1 (Page No 189) of NCERT Class 7 Math Chapter 12 Symmetry –
1. Copy the figures with punched holes and find the axes of symmetry for the following:
(a) The figure is shown below:
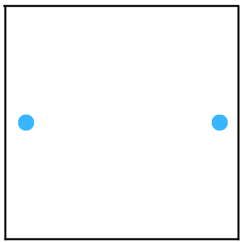
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 2 lines of symmetry as shown below:
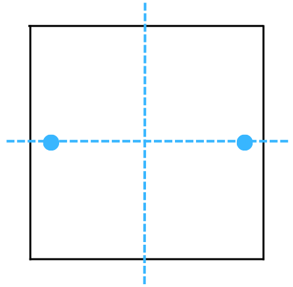
(b) The figure is shown below:

Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). Therefore, the above figure has 1 line of symmetry as shown below:
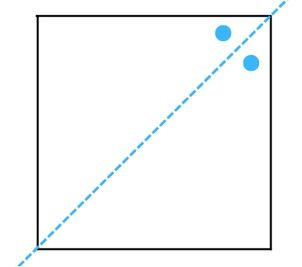
(c) The figure is shown below:

Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 1 line of symmetry as shown below:
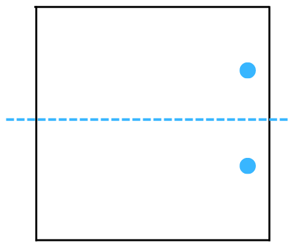
(d) The figure is shown below:
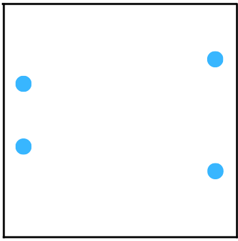
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). Therefore, the above figure has 1 line of symmetry as shown below:

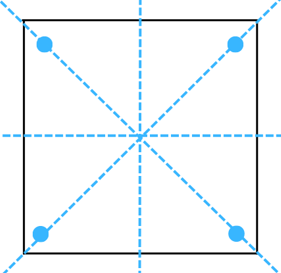
(e) The figure is shown below:

Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 4 lines of symmetry as shown below:
(f) The figure is shown below:
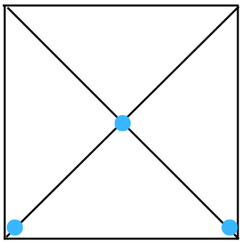
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). Therefore, the above figure has 1 line of symmetry as shown below:
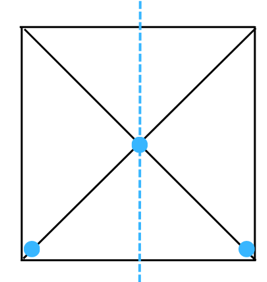
(g) The figure is shown below:
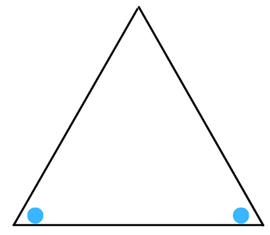
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 1 line of symmetry as shown below:
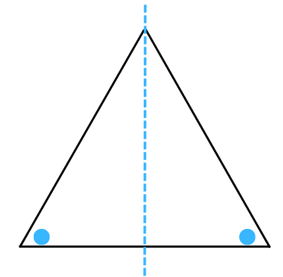
(h) The figure is shown below:

Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). Therefore, the above figure has 1 line of symmetry as shown below:
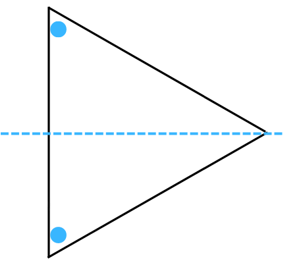
(i) The figure is shown below:

Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 1 line of symmetry as shown below:
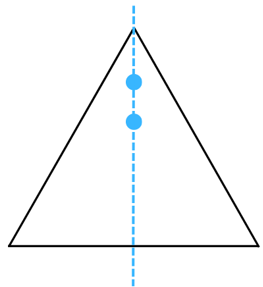
(j) The figure is shown below:
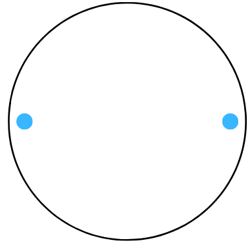
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 2 lines of symmetry as shown below:

(k) The figure is shown below:
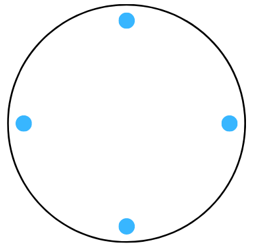
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 4 lines of symmetry as shown below:
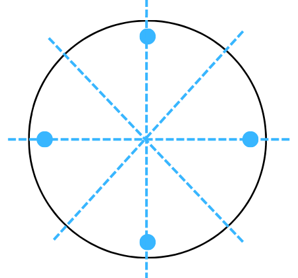
(l) The figure is shown below:
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
Therefore, the above figure has 1 line of symmetry as shown below:
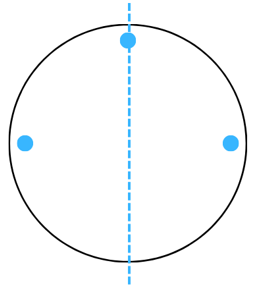
2. Given the line(s) of symmetry, find the other hole(s):
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). Therefore, all the figures with the other hole marked in each are shown below:
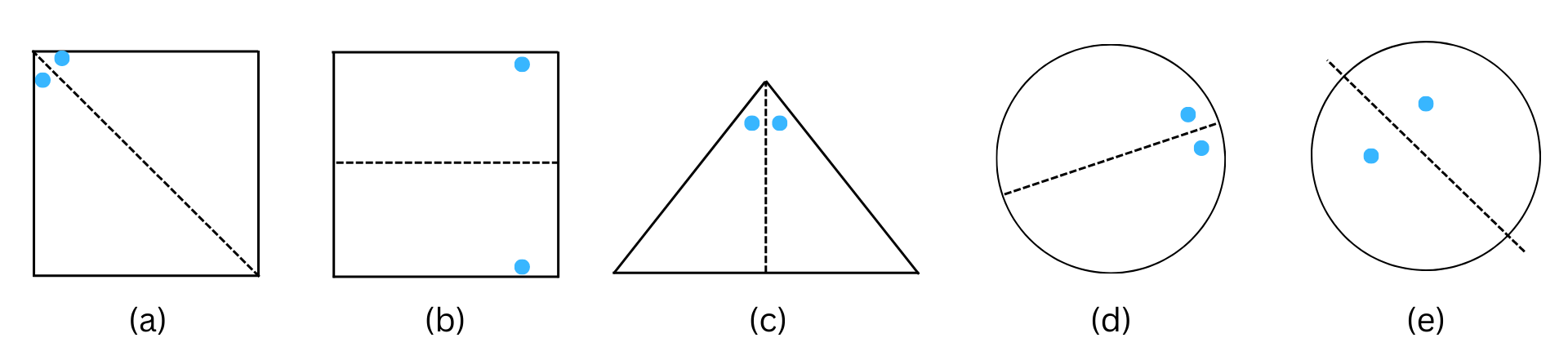
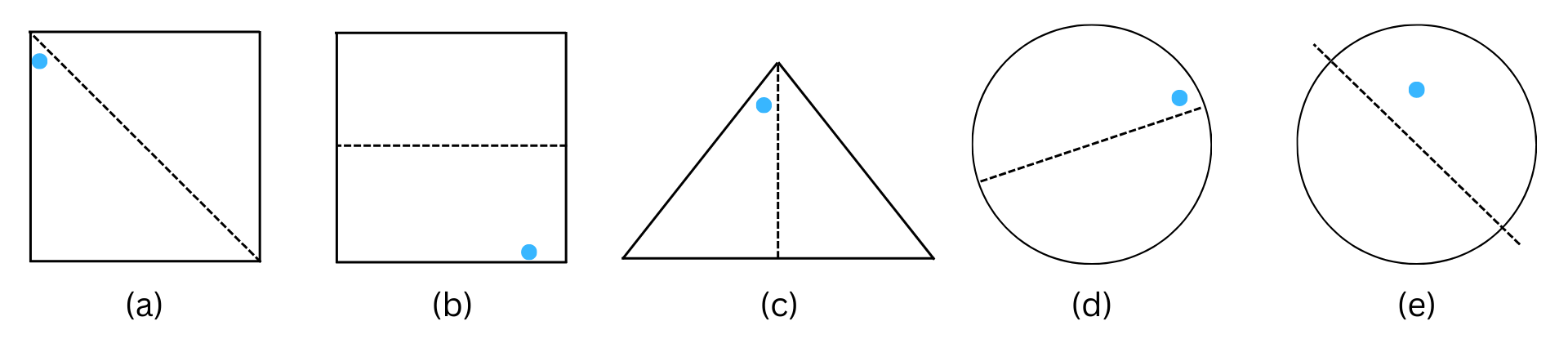
3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
Answer:
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
The complete figures after reflection are shown below:
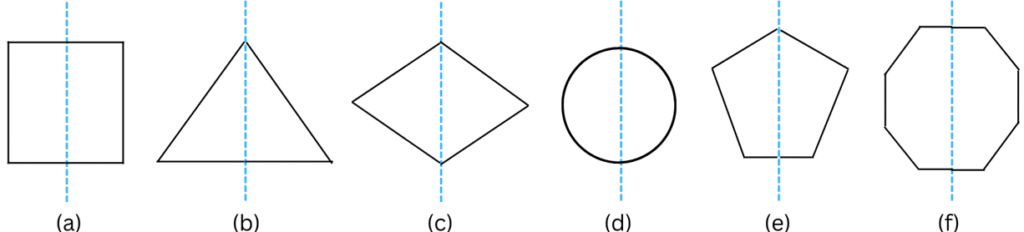
The names of the completed figures are as follows:
(a) is a square.
(b) is a triangle.
(c) is a rhombus.
(d) is a circle.
(e) is a pentagon. (f) is an octagon.
4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
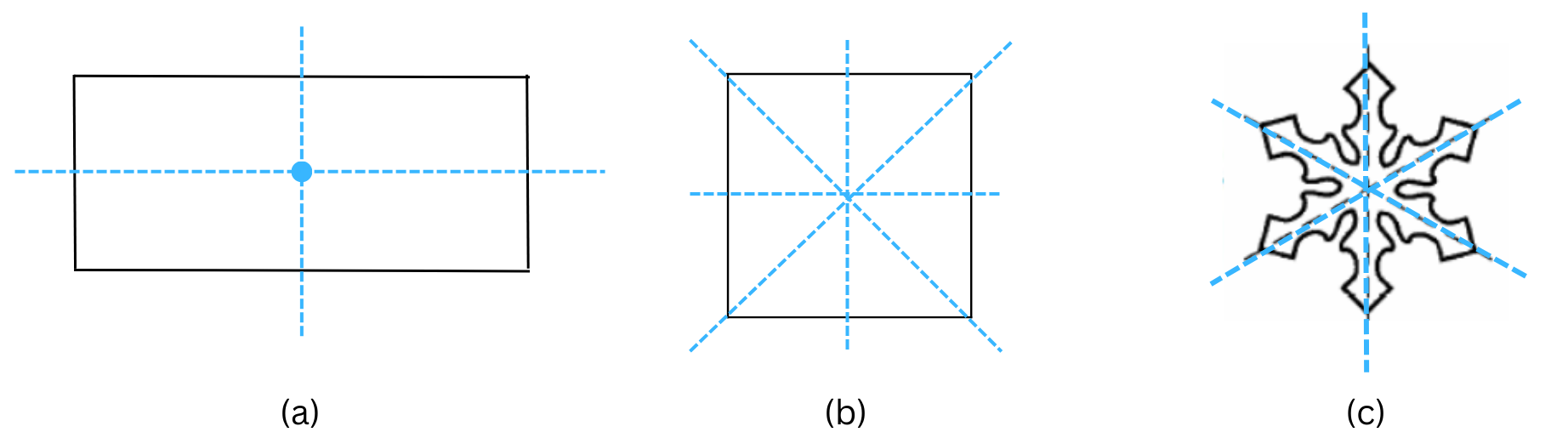
Identify multiple lines of symmetry, if any, in each of the following figures:
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded).
The completed figures with the multiple lines of symmetry are shown below:
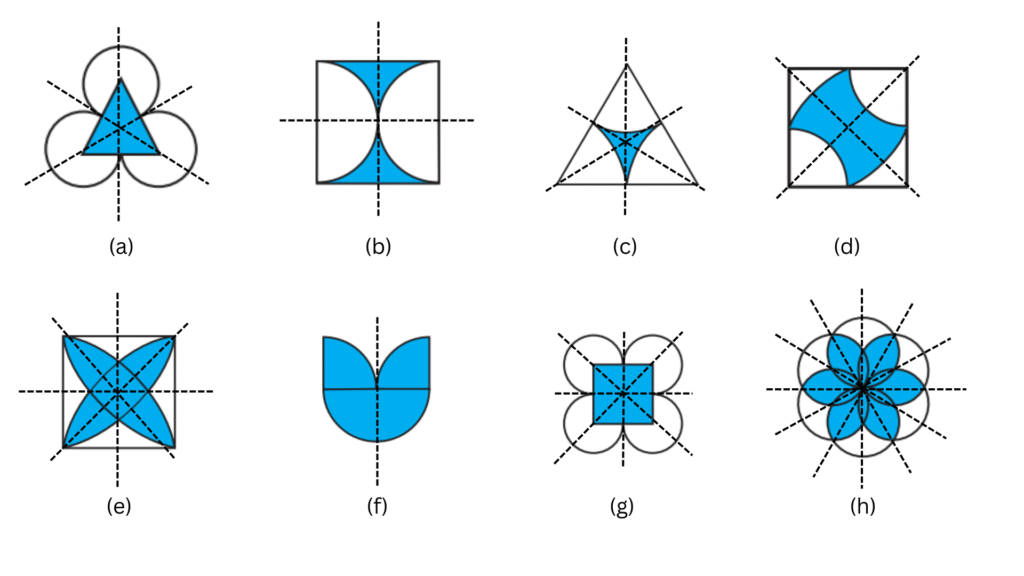
Figure (a) has 3 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (b) has 2 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (c) has 3 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (d) has 2 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (e) has 4 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (f) has 1 line of symmetry, so it does not have multiple lines of symmetry.
Figure (g) has 4 lines of symmetry, so we can say it has multiple lines of symmetry.
Figure (h) has 6 lines of symmetry, so we can say it has multiple lines of symmetry.
5. Copy the figure given here.

Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
Answer:
We take any one diagonal and shade the appropriate squares in grey to make the figure symmetric about it. As you can see in the completed figure below, there is more than one way to do that – we can make the figure symmetric about the other diagonal too by shading the appropriate squares. Therefore, the figure is symmetric about both diagonals.
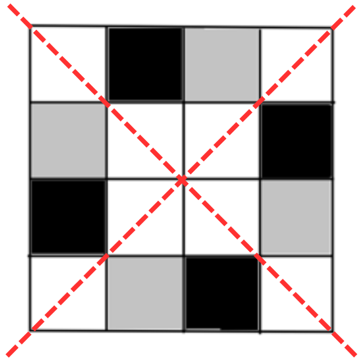
Although not specifically asked in the question, it is interesting to note that the figure has 2 more lines of symmetry as shown below:
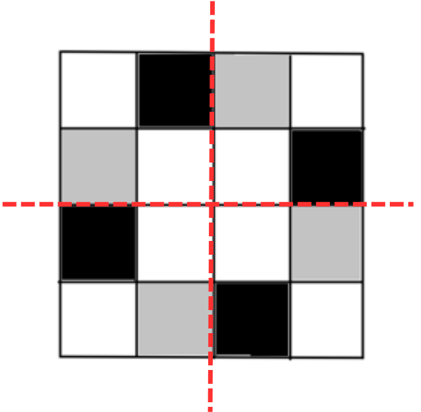
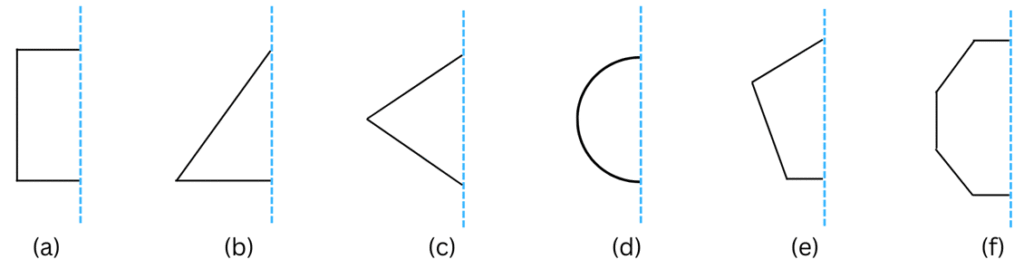
6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
Answers:
(a) The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). The line of symmetry can also be thought of as a mirror line – about which one half is the mirror image of the other.
The completed shape which is symmetric about the mirror line is shown below (note how we take into account the left-right changes in orientation due to reflection):

(b) The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). The line of symmetry can also be thought of as a mirror line – about which one half is the mirror image of the other.
There are two lines of symmetry here and we have to make the shape symmetric about both. The completed shape which is symmetric about the mirror line is shown below (note how we take into account the left-right changes in orientation due to reflection):
(c) The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). The line of symmetry can also be thought of as a mirror line – about which one half is the mirror image of the other.
There are two lines of symmetry here and we have to make the shape symmetric about both. The completed shape which is symmetric about the mirror line is shown below (note how we take into account the left-right changes in orientation due to reflection):
7. State the number of lines of symmetry for the following figures:
(a) An equilateral triangle
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). An equilateral triangle has 3 lines of symmetry as shown below:

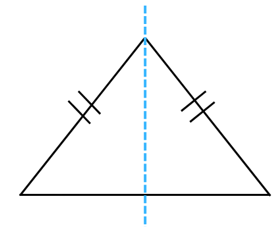
(b) An isosceles triangle
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). An isosceles triangle has 1 line of symmetry as shown below:
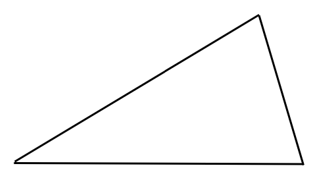
(c) A scalene triangle
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to examine the scalene triangle below and conclude that it has no lines of symmetry.
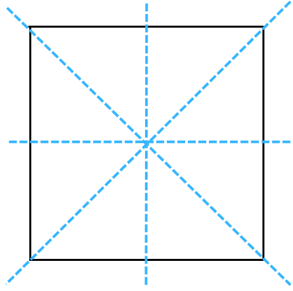
(d) A square
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). A square has 4 lines of symmetry as shown below:
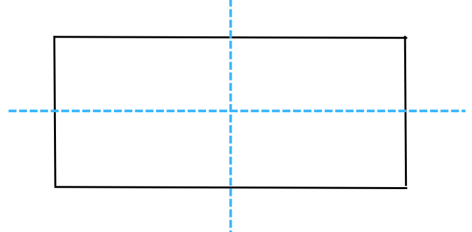
(e) A rectangle
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). A rectangle has 2 lines of symmetry as shown below:
(f) A rhombus
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). A rhombus has 2 lines of symmetry as shown below:
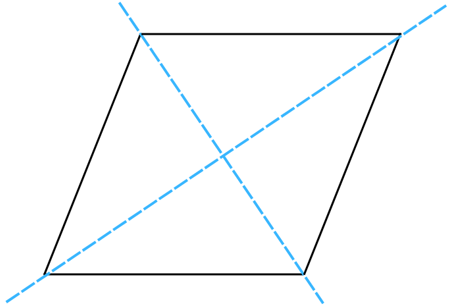
(g) A parallelogram
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to examine the parallelogram below and conclude that it has no lines of symmetry.

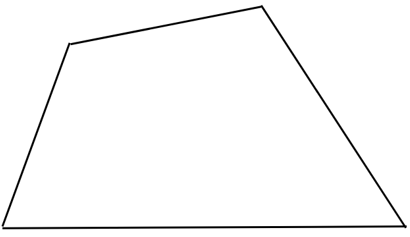
(h) A quadrilateral
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to examine the quadrilateral below and conclude that it has no lines of symmetry.
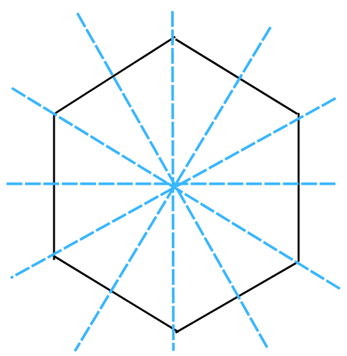
(i) A regular hexagon
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). A regular hexagon has 6 lines of symmetry as shown below:
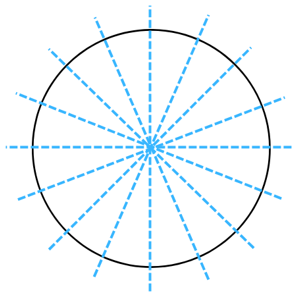
(j) A circle
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to see that we can draw as many lines of symmetry as we want through the centre of a circle. Therefore, a circle can have an infinite number, i.e an innumerable number of lines of symmetry passing through the centre of the circle. Just a few of them are shown below:
8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
(a) a vertical mirror
Answer: The letters which have reflectional symmetry about a vertical mirror are A, H, I, M, O, T, U, V, W, X, Y. The vertical line of symmetry or the vertical mirror line is represented by the dashed line as shown below:
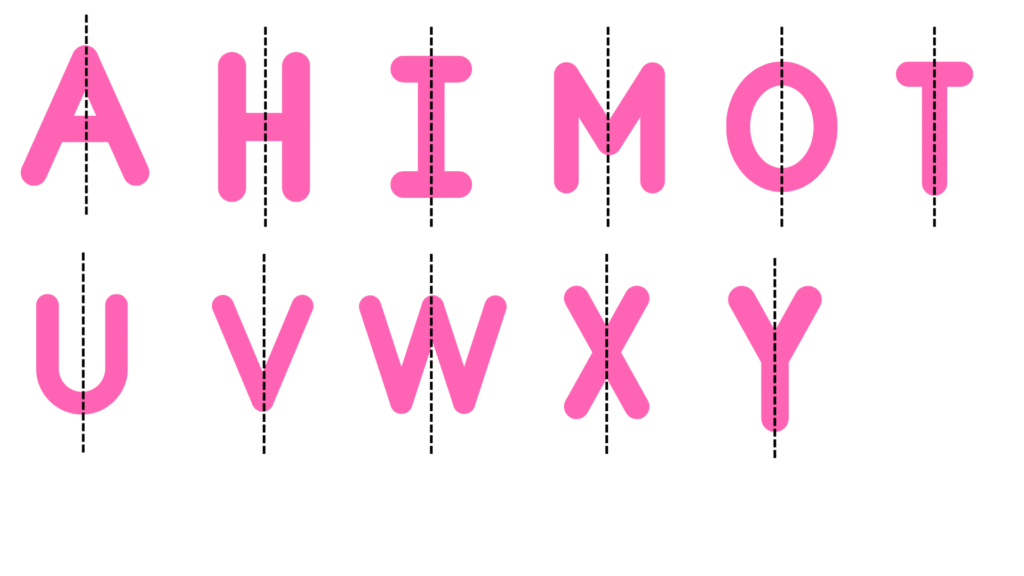
(b) a horizontal mirror
Answer: The letters which have reflectional symmetry about a horizontal mirror are B, C, D, E, H, I. The horizontal line of symmetry or the horizontal mirror line is represented by the dashed line as shown below:
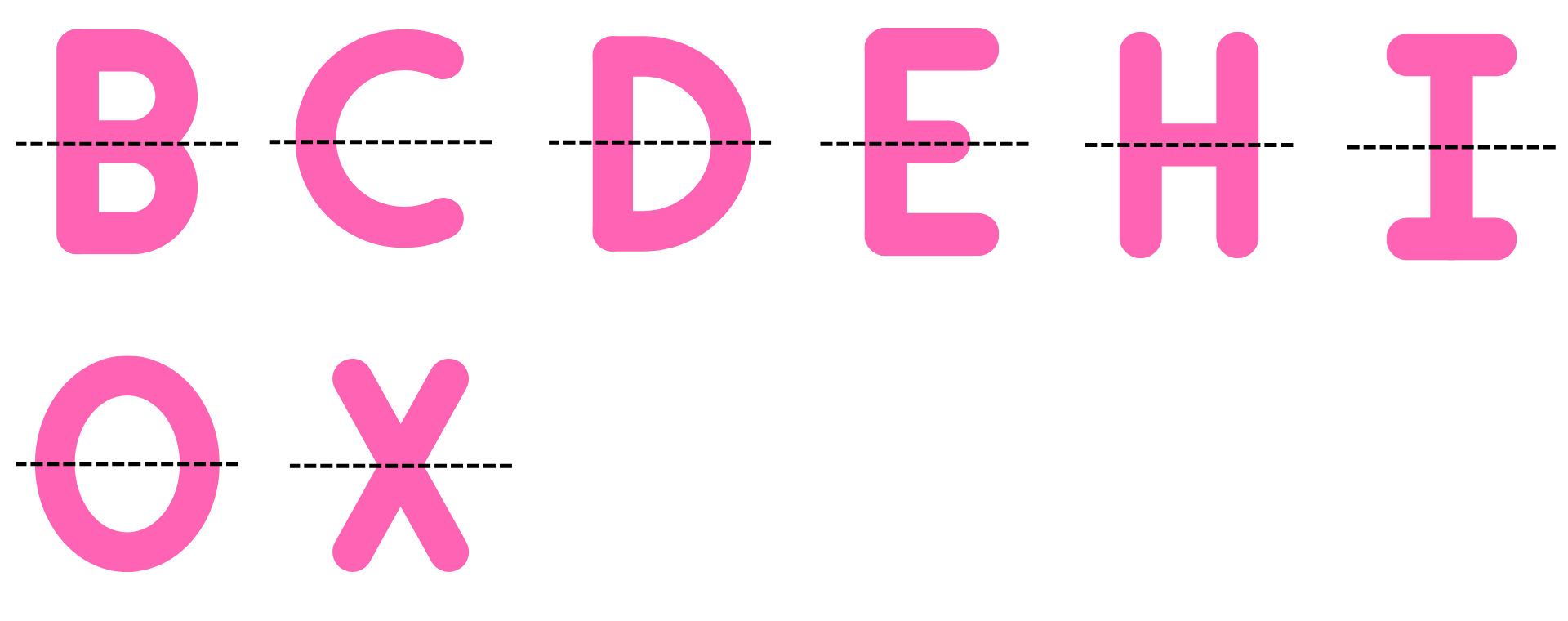
(c) both horizontal and vertical mirrors
Answer: The letters which have reflectional symmetry about both horizontal and vertical mirrors are O, X, I, H. The horizontal and vertical lines of symmetry or the horizontal and vertical mirror lines are represented by the dashed line as shown below:

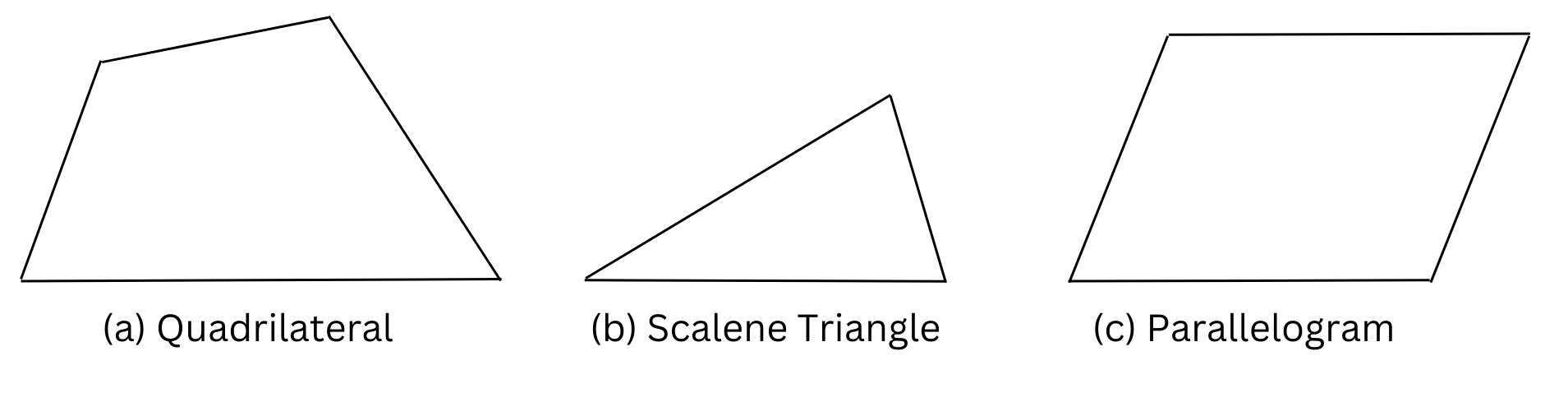
9. Give three examples of shapes with no line of symmetry.
Answer:
A scalene quadrilateral, a scalene triangle and a parallelogram have no line of symmetry.
The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to confirm using the figures below that these shapes have no such line of symmetry.
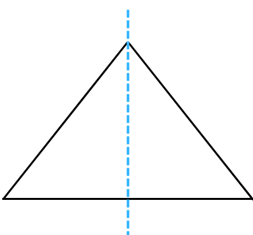
10. What other name can you give to the line of symmetry of
(a) an isosceles triangle?
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to see that the line of symmetry of an isosceles triangle is the median or altitude (the median and altitude is the same in case of an isosceles triangle).
(b) a circle?
Answer: The line of symmetry is the line(s) about which the figure may be folded so that the two parts coincide (after being folded). It is easy to see that the lines of symmetry of a circle all pass through the centre and is actually the diameter of the circle.
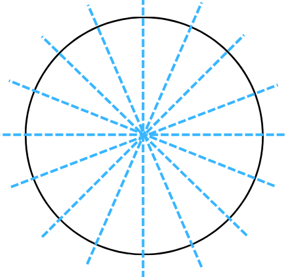
Solutions to Exercise 12.2 (Page No 195) of NCERT Class 7 Math Chapter 12 Symmetry –
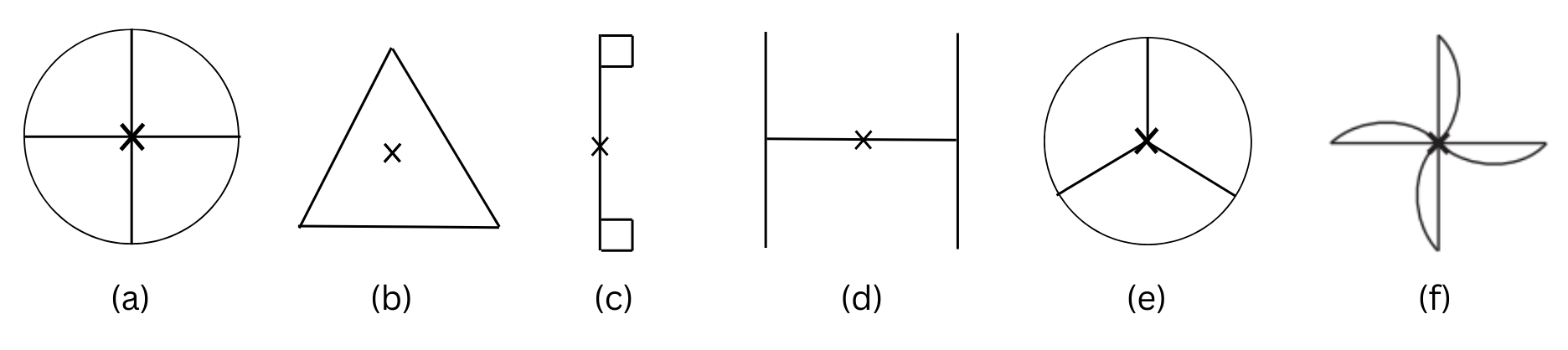
1. Which of the following figures have rotational symmetry of order more than 1:
Answers:
(a) We turn Figure (a) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely four positions (on rotation through the angles 900, 1800, 2700 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 4.

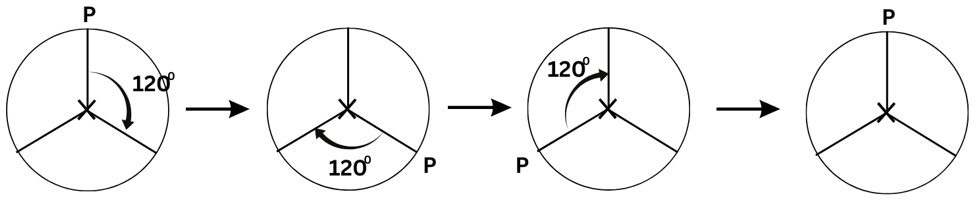
(b) We turn Figure (b) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely three positions (on rotation through the angles 1200, 2400 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 3.

(c) We turn Figure (c) about the centre of rotation (marked with an X). In a full 3600 turn, there is just one position (on rotation through the angle 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 1.

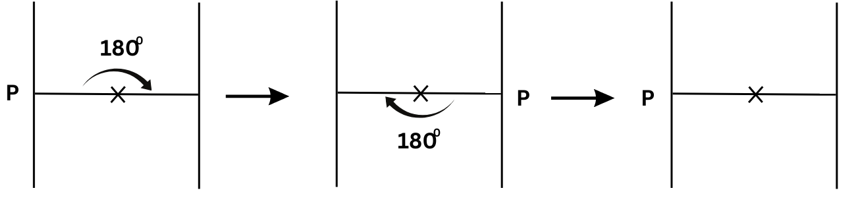
(d) We turn Figure (d) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
(e) We turn Figure (e) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely three positions (on rotation through the angles 1200, 2400 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 3.
(f) We turn Figure (e) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely four positions (on rotation through the angles 900, 1800, 2700 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 4.

Therefore. we conclude that the figures (a), (b), (d), (e), (f).
2. Give the order of rotational symmetry for each figure:
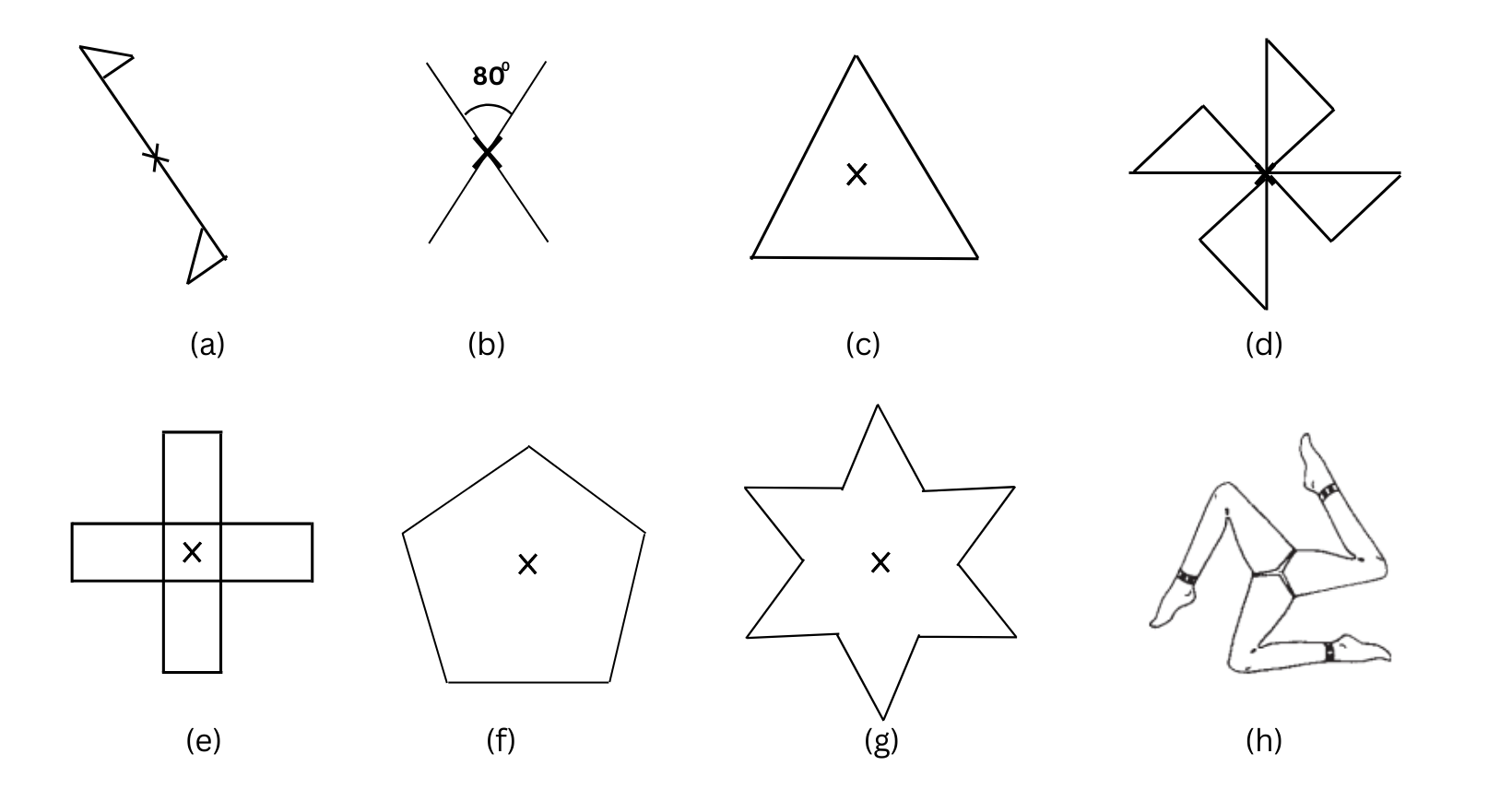
Answers:
(a) We turn Figure (a) about the centre of rotation (marked with an X). In a full 3600 turn, there is just one position (on rotation through the angle 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 1.
(b) We turn Figure (b) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
(c) We turn Figure (c) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely three positions (on rotation through the angles 1200, 2400 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 3.
(d) We turn Figure (d) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely four positions (on rotation through the angles 900, 1800, 2700 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 4.

(e) We turn Figure (e) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely four positions (on rotation through the angles 900, 1800, 2700 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 4.

(f) We turn Figure (f) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely five positions (rotating the figure clockwise by an angle of 720 each time) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 5.
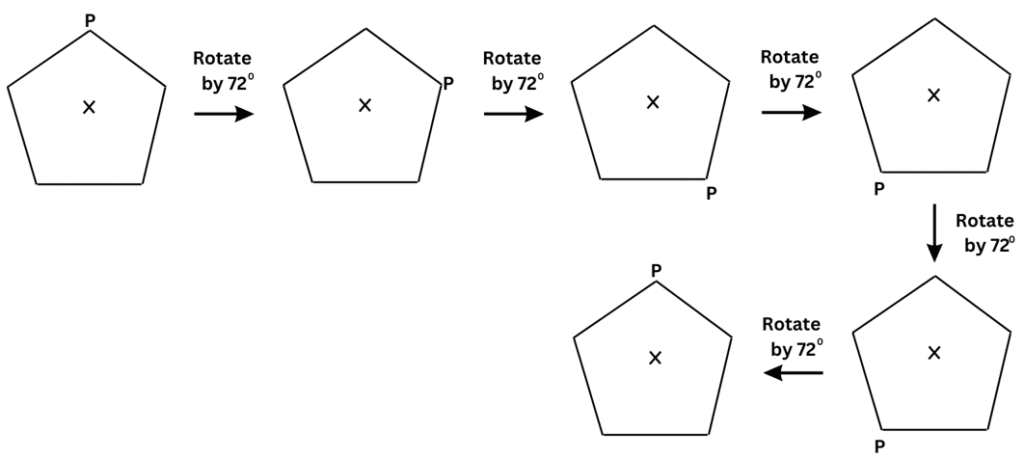
(g) We turn Figure (g) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely six positions when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 6.
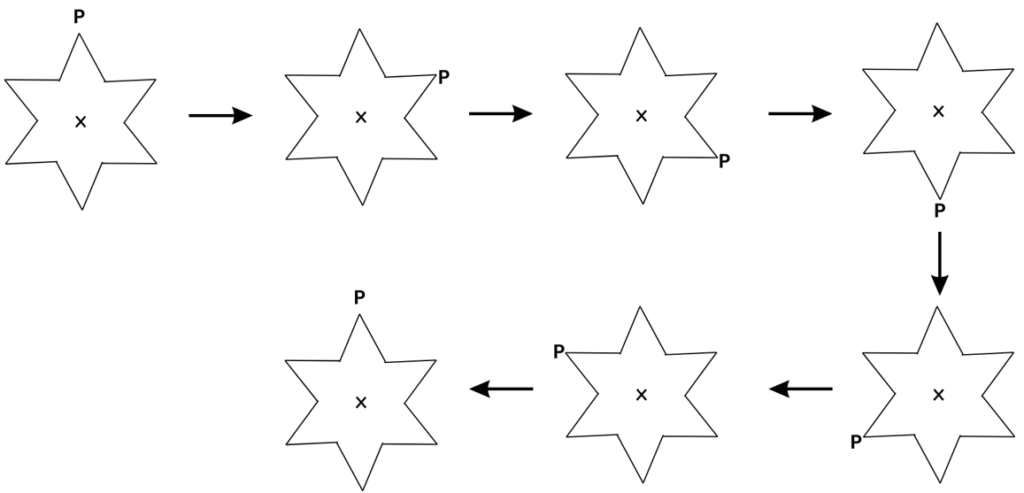
(h) We turn Figure (c) about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely three positions (on rotation through the angles 1200, 2400 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 3.

Solutions to Exercise 12.3 (Page No 196) of NCERT Class 7 Math Chapter 12 Symmetry –
1. Name any two figures that have both line symmetry and rotational symmetry.
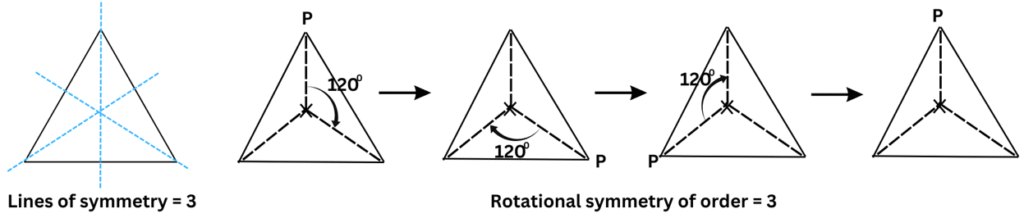
Answer: Two figures that have both line symmetry and rotational symmetry are an equilateral triangle and a circle.
In an equilateral triangle has 3 lines of symmetry (marked in blue dashed lines) and rotational symmetry of order = 3 as shown below:
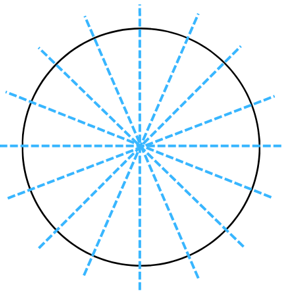
A circle has infinite (i.e innumerable) lines of symmetry some of which are marked below in blue dashed lines. Also, it is easy to see that when you rotate a circle about its centre, at every point the circle will look exactly the same. Therefore, it is easy to see that a circle has rotational symmetry of order = infinity.
2. Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
Answer:
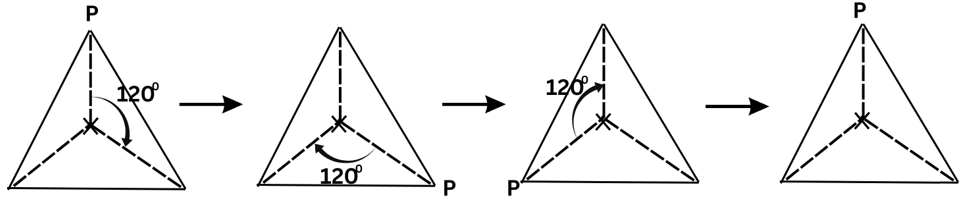
An equilateral triangle has both line and rotational symmetries of order more than 1.
It has 3 lines of symmetry as shown below:
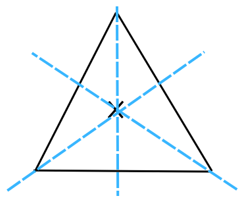
It has a rotational symmetry of order = 3 as shown below:
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
Answer:
An isosceles triangle has only line symmetry and does not have rotational symmetry of order more than 1.
It has 1 line of symmetry as shown below:
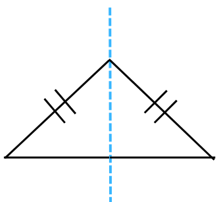
If you rotate the triangle by any angle of rotation between 00 and 3600, you will find that it will never look the same. An example is shown below:

(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
Answer:
A parallelogram is a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
It is easy to see from the figure below that a parallelogram has no lines of symmetry:
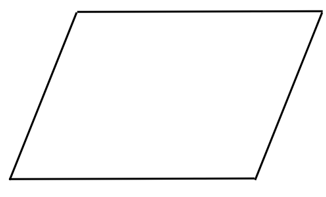
We rotate the parallelogram about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.

(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Answer: An isosceles trapezium (non-parallel) sides equal has 1 line of symmetry (marked with the blue dashed line), but a rotational symmetry of order only = 1. If you rotate it by any angle of rotation between 00 and 3600, you will find that it will look the same only at an angle of 360o. The line of symmetry is shown below:

3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer:
Yes, you will find that if you rotate a figure which has two or more lines of symmetry through the full 3600 there will be more than one situation when the figure will look exactly the same. So yes, it will indeed have rotational symmetry of order more than 1. The exact order will depend on the specific figure.
4. Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular Hexagon | |||
| Circle | |||
| Semi-circle |
Answer: The completed table is shown below:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | Point of intersection of diagonals. | 4 | 900 |
| Rectangle | Point of intersection of diagonals | 2 | 1800 |
| Rhombus | Point of intersection of diagonals | 2 | 1800 |
| Equilateral Triangle | Point of intersection of medians or altitudes. | 3 | 1200 |
| Regular Hexagon | Point of intersection of diagonals | 6 | 600 |
| Circle | Centre | Infinite | Any angle |
| Semi-circle | Centre | 1 | 3600 |
5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Answer:
The quadrilaterals which have both line and rotational symmetry of order more than 1 are the square, rectangle and rhombus.
The square has 4 lines of symmetry (marked in blue dashed lines) as shown below:
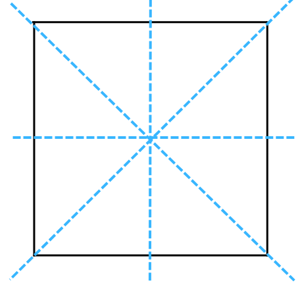
We turn the square about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely four positions (on rotation through the angles 900, 1800, 2700 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 4.

The rectangle has 2 lines of symmetry (marked in blue dashed lines) as shown below:
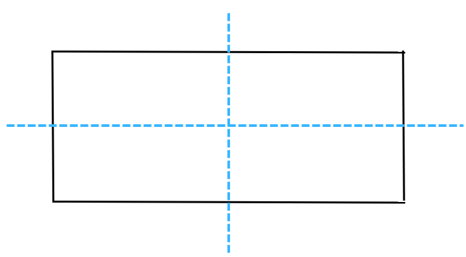
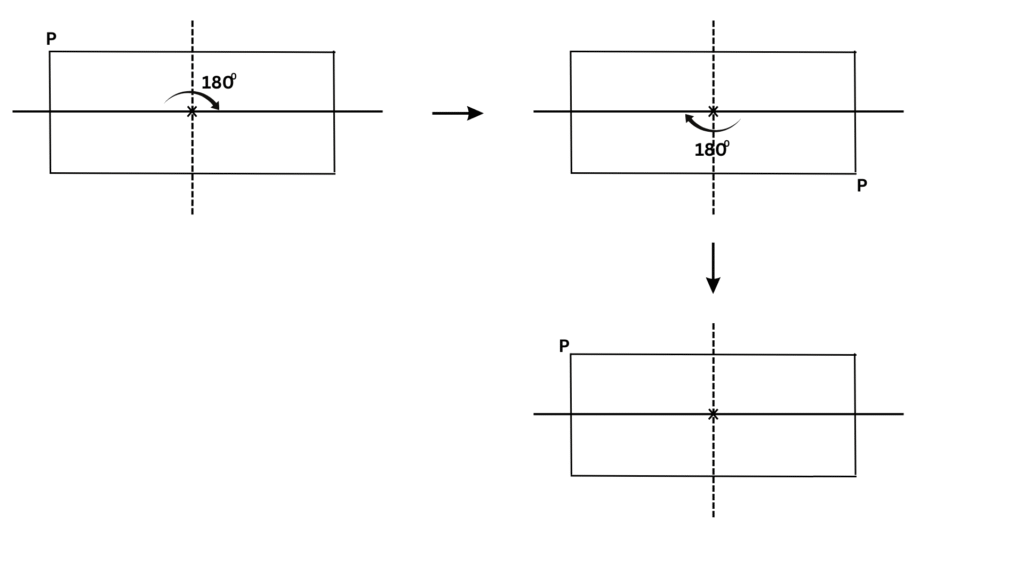
We turn the rectangle about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
The rhombus has 2 lines of symmetry (marked in blue dashed lines) as shown below:
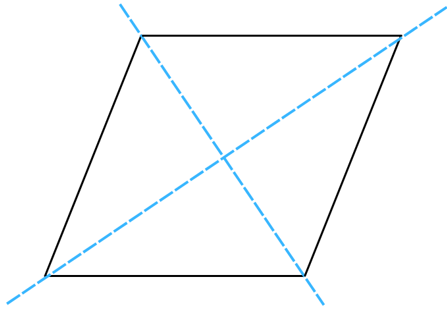
We turn the rhombus about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
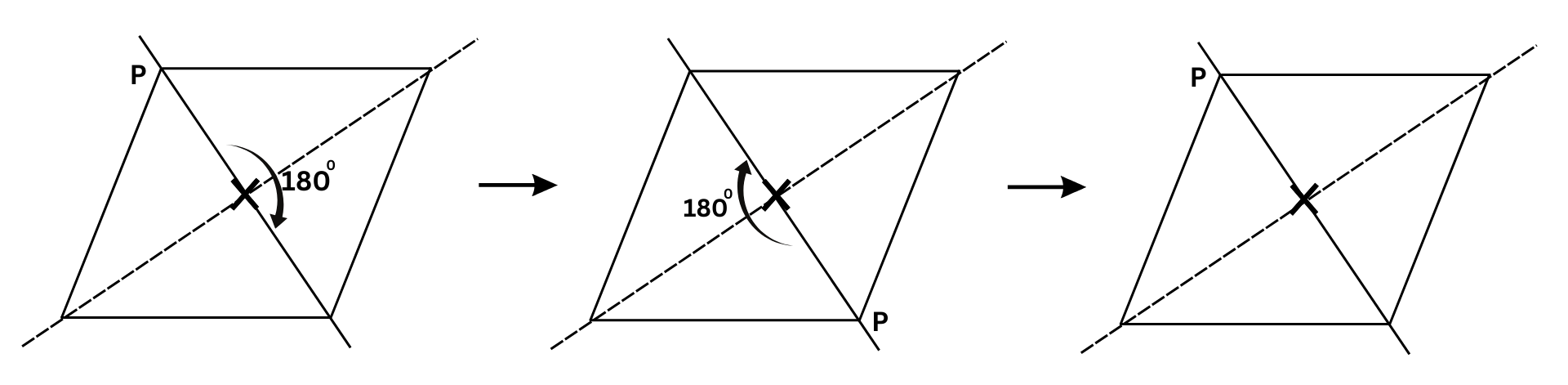
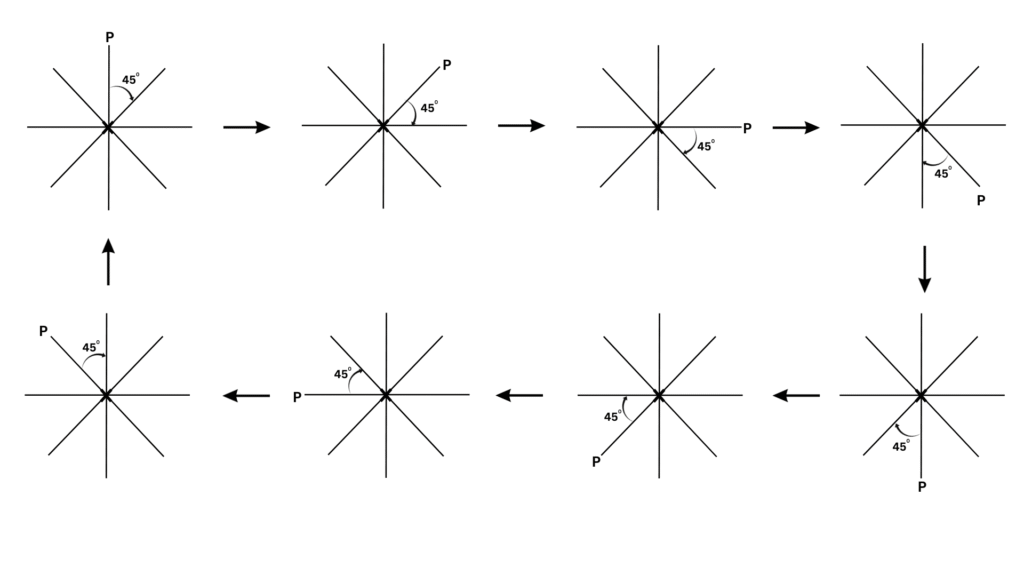
6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer:
You will observe that if a figure looks exactly the same after being rotated by an angle of 600, it will look the same if you keep rotating it successively by 600. Therefore, the other angles for which the figure looks exactly the same are: 1200, 2400, 3000 and 3600.
7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°? (ii) 17°?
Answers:
The trick here is to see if the angle of rotation exactly divides 3600. You will observe for a shape that if the angle of rotation exactly divides 3600, it can have a rotational symmetry of order more than 1, otherwise not.
(i) In case of the angle 450, we can that 450 exactly divides 3600. Therefore, we can say that a rotational symmetry of order more than 1 can exist.
(ii) In case of the angle 170, we can that 170 does not exactly divide 3600. Therefore, we can say that a rotational symmetry of order more than 1 cannot exist.
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 12 Symmetry:
Very Short Answer Type Questions:
1. Are the number of lines of symmetry and order of rotational symmetry always the same?
Answer:
No, the lines of symmetry and order of rotational symmetry can be different.
2. Name a triangle which has no lines of symmetry.
Answer:
A scalene triangle has no lines of symmetry.
3. Do all objects have rotational symmetry of order more than 1?
Answer:
No, many objects have rotational symmetry of order 1.
4. Does size of a triangle change the lines of symmetry and rotational symmetry?
Answer:
No, size of the triangle does not change the lines of symmetry and rotational symmetry
5. How many more lines of symmetry does a square have than a rectangle?
Answer:
A square has 4 lines of symmetry and a rectangle has 2 lines of symmetry. Therefore, a square has (4 – 2) = 2 lines of symmetry more than that of a rectangle.
6. How many lines of symmetry does the symbol ‘?’ have?
Answer:
It has no lines of symmetry.
7. What is the relationship between the number of sides in a regular polygon and the number of lines of symmetry?
Answer:
The number of lines of symmetry is equal to the number of sides in a polygon.
8. How many lines of symmetry does an angle have?
Answer:
An angle has one line of symmetry.
9. Which of the letters B, C, D, V have a vertical line of symmetry?
Answer:
The letter V has a vertical line of symmetry.
10. Two parallel line segments of equal length are positioned one above the other. How many lines of symmetries does the overall structure have?
Answer:
The overall structure has one vertical line of symmetry and one horizontal line of symmetry.
Short and Long Answer Type Questions:
1. Show the lines of symmetry for letters A and X.
Answer:
A has 1 line of symmetry and X has two lines of symmetry as shown below:
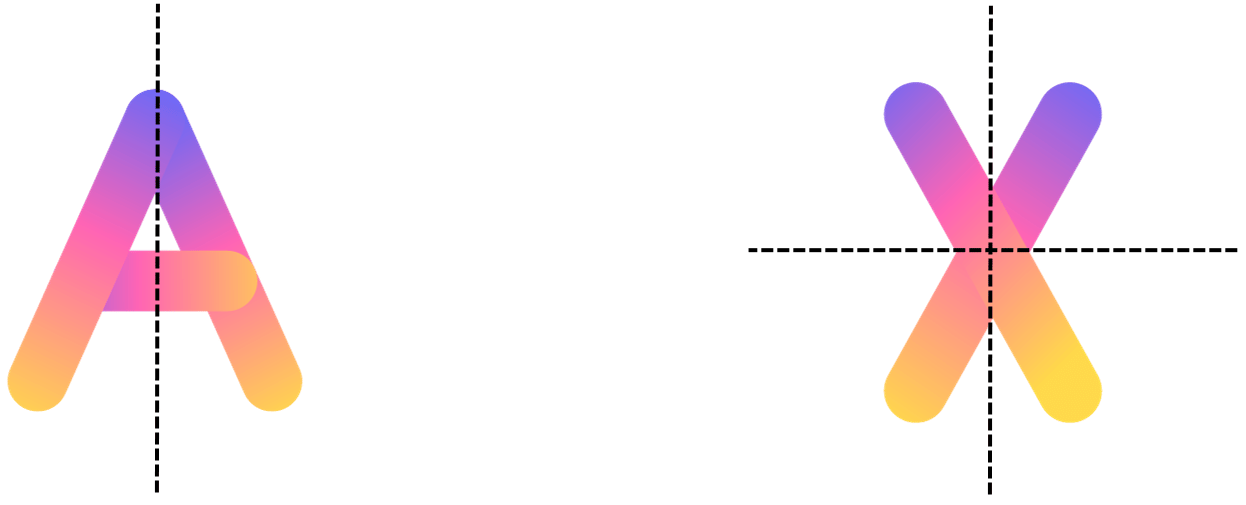
2. Find the order of rotational symmetry for the following figure:
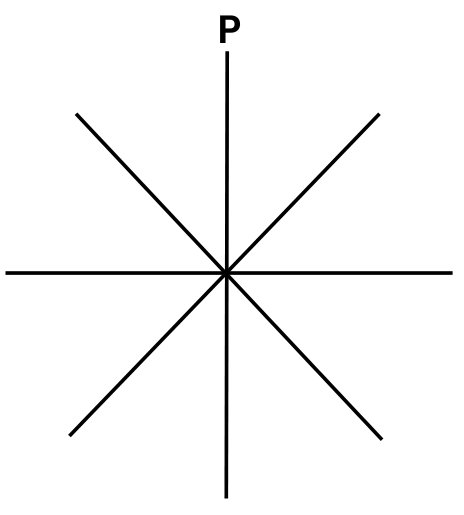
Answer:
We turn the above figure about the centre of rotation (marked with an X). If you rotate the figure successively by angles of 450 there are precisely eight positions when the figure looks exactly the same in a full 3600 turn. Because of this, we can say that it has a rotational symmetry of order 8.
3. State the number of lines of symmetry and order of rotational symmetry for the figure below:
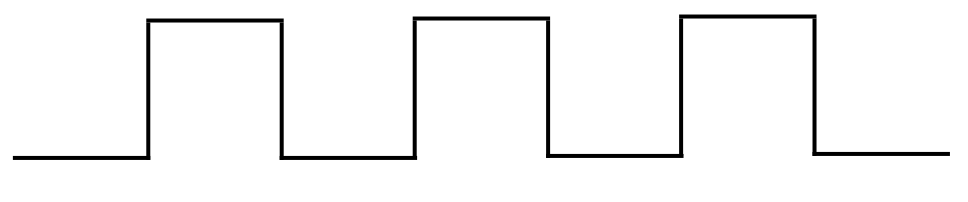
Answer:
The number of lines of symmetry for the above figure is one:
If you rotate the figure by any angle of rotation between 00 and 3600, you will find that it will never look the same. Therefore, it has a rotational symmetry of order only = 1.
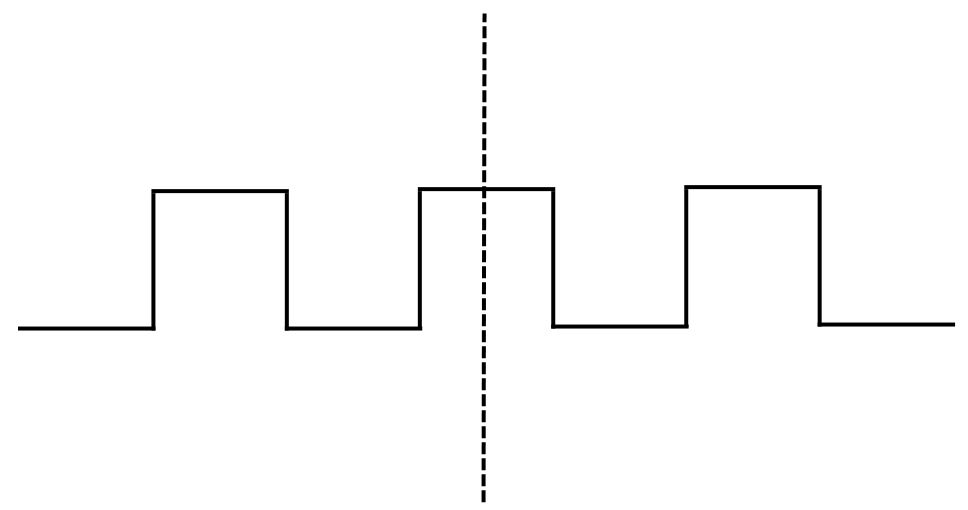
4. State the number of lines of symmetry and order of rotational symmetry for the figure below:
Answer:
The lines of symmetry for the figure = 2.
We rotate the figure about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
5. State the number of lines of symmetry and order of rotational symmetry for the figure below:

Answer:
The lines of symmetry for the figure = 2.
We rotate the figure about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.
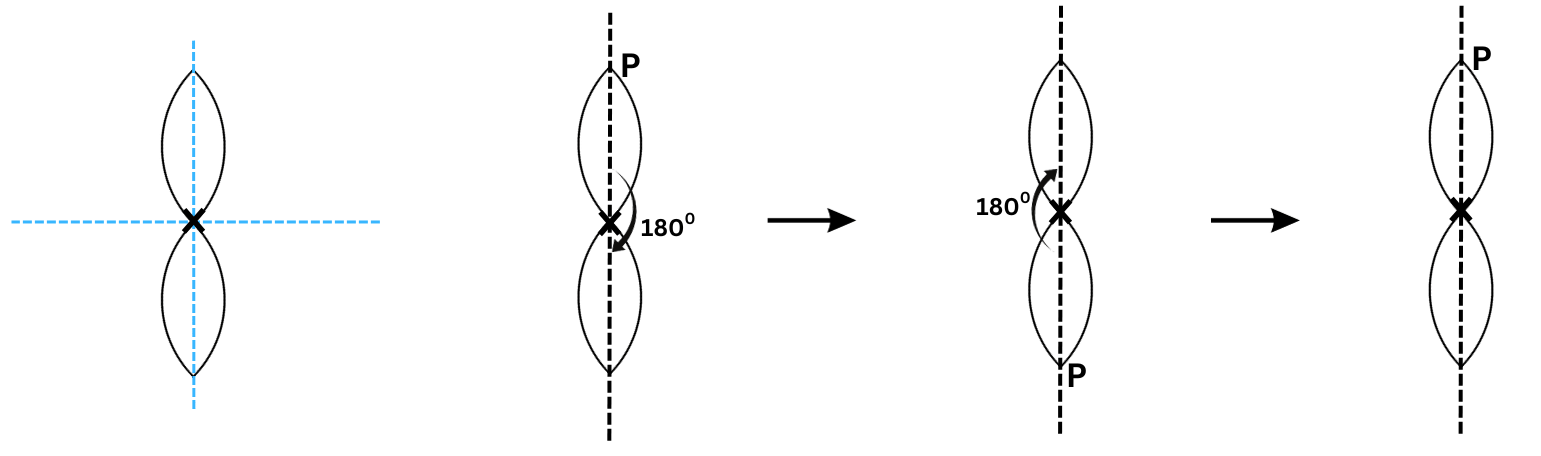
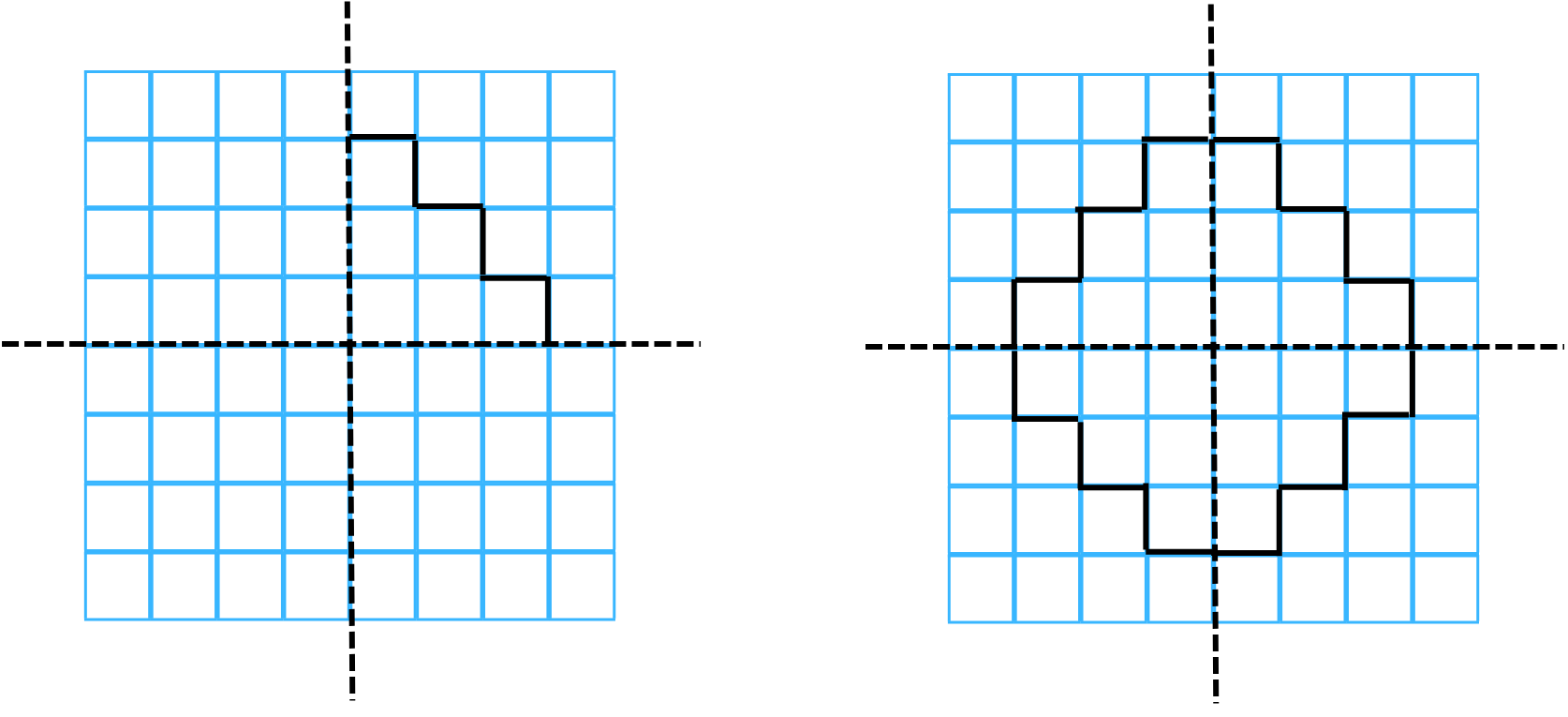
6. Make the shape below symmetric about the two mirror lines.
Answer: The completed shape which is symmetric about the mirror lines is shown below (note how we take into account the left-right changes in orientation due to reflection):
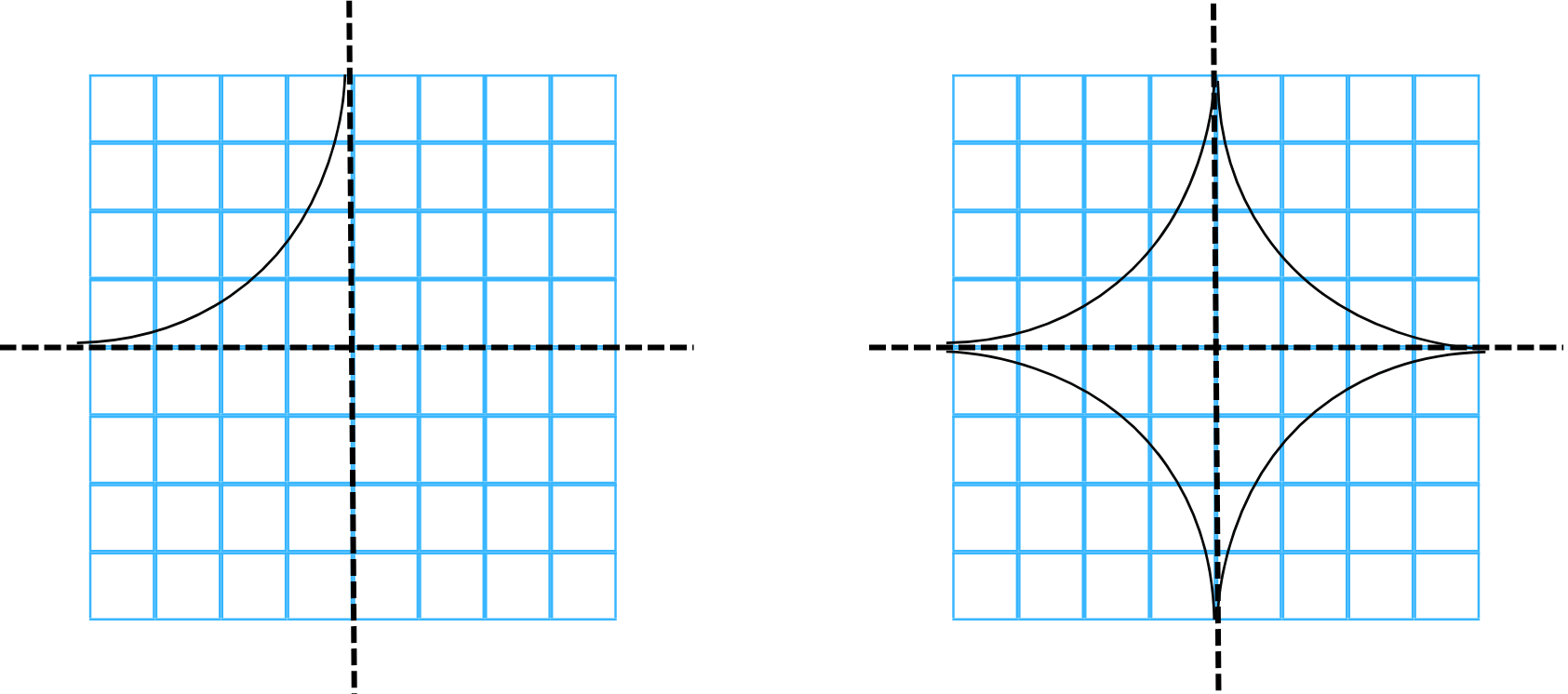
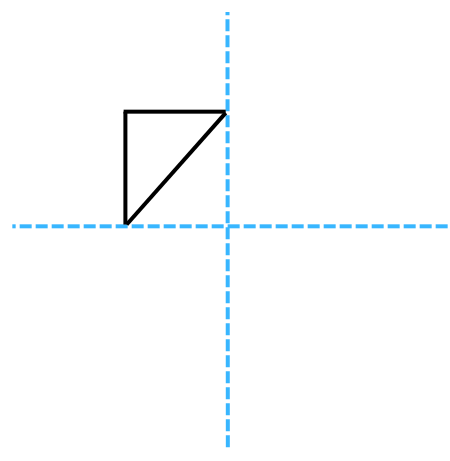
7. (a) For the figure shown in (a) find the lines of symmetry.
(b) Make the shape symmetric about the horizontal mirror line as in (b).

Answer:
(a) The figure shown in (a) has one vertical line of symmetry as shown below:
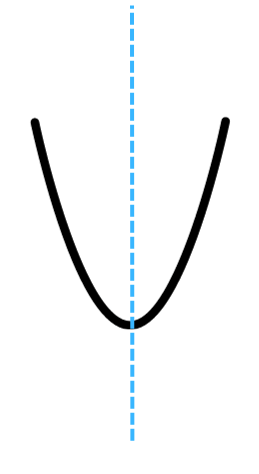
(b) The completed shape which is symmetric about the horizontal mirror line is shown below:

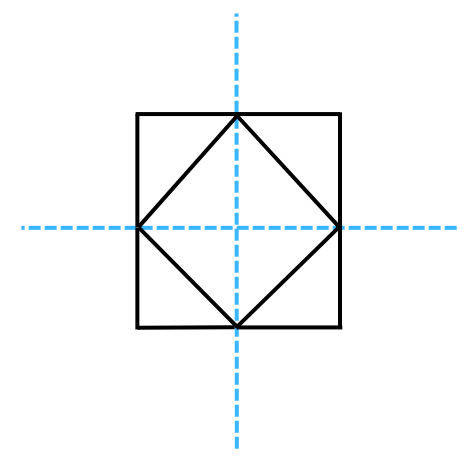
8. State the number of lines of symmetry and order of rotational symmetry for the figure below:
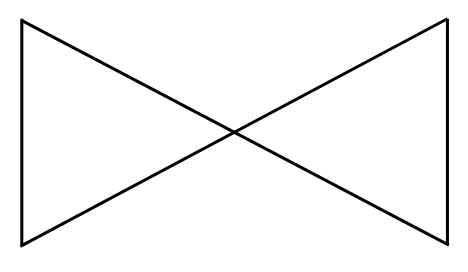
Answer:
The lines of symmetry for the figure = 2.
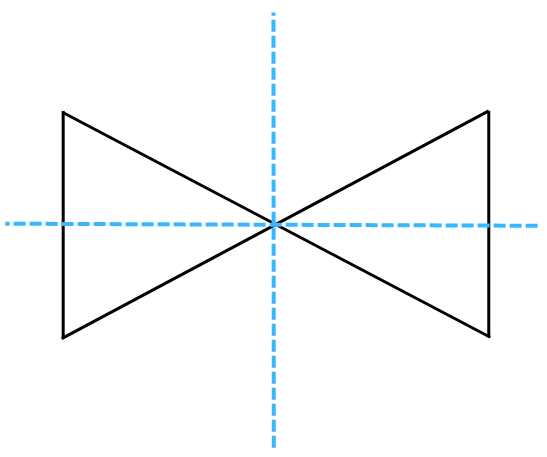
We rotate the figure about the centre of rotation (marked with an X). In a full 3600 turn, there are precisely two positions (on rotation through the angles 1800 and 3600) when the figure looks exactly the same. Because of this, we can say that it has a rotational symmetry of order 2.

9. State the number of lines of symmetry and order of rotational symmetry for the figure below:
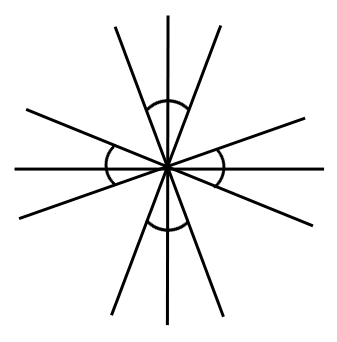
Answer:
The lines of symmetry for the figure = 4.
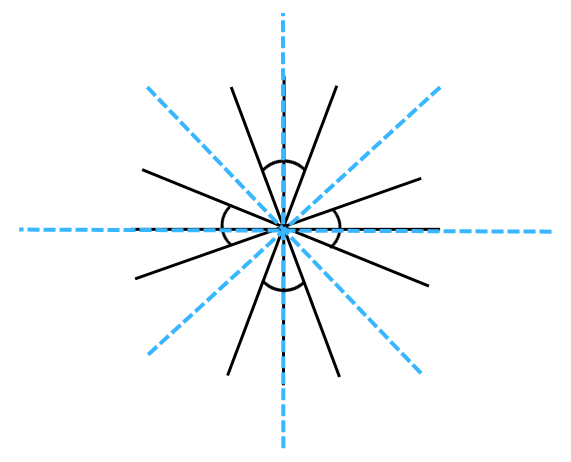
We turn the above figure about the centre of rotation (marked with an X). If you rotate the figure successively by angles of 900 there are precisely four positions when the figure looks exactly the same in a full 3600 turn. Because of this, we can say that it has a rotational symmetry of order 4.
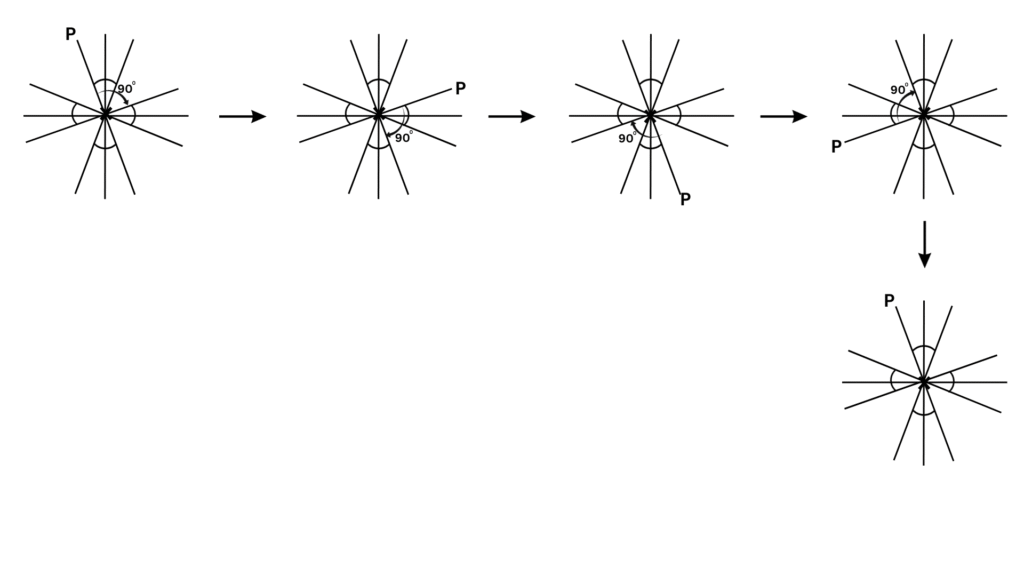
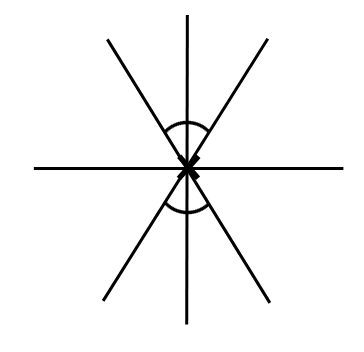
10. State the number of lines of symmetry and order of rotational symmetry for the figure below:
Answer:
The lines of symmetry for the figure = 3.
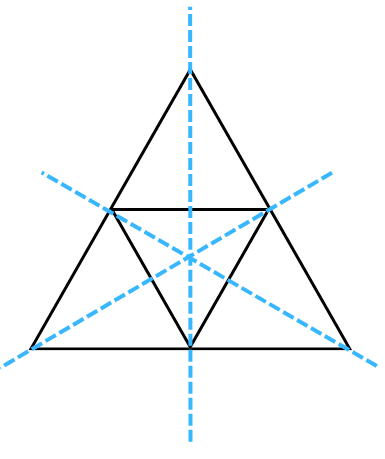
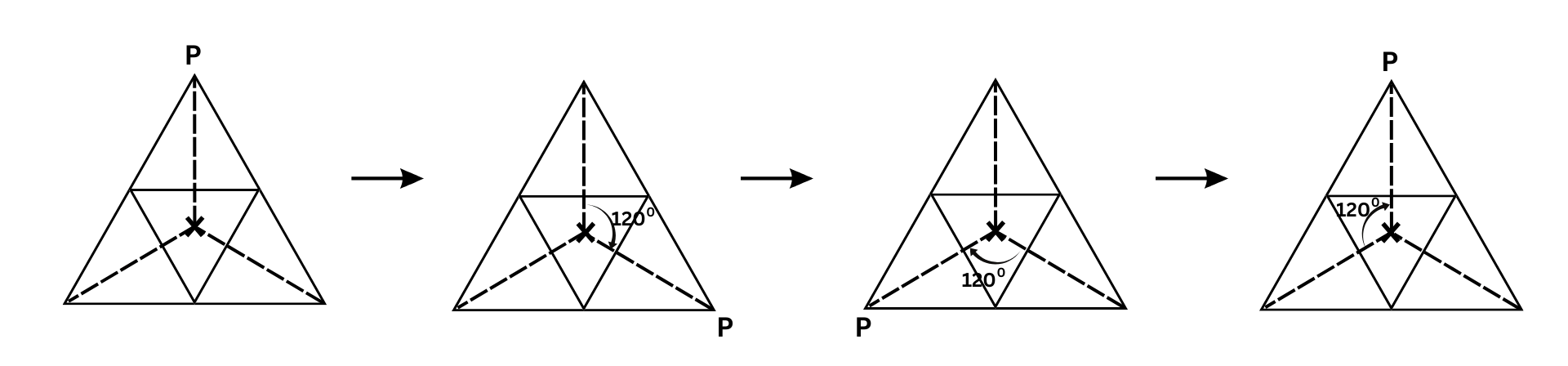
We turn the above figure about the centre of rotation (marked with an X). If you rotate the figure successively by angles of 1200 there are precisely three positions when the figure looks exactly the same in a full 3600 turn. Because of this, we can say that it has a rotational symmetry of order 3.
Fill in the Blanks:
(a) All objects have rotational symmetry of order _________.
(b) An icecream cone has _________ line of symmetry.
(c) Centre of rotation of a square lies at the point of intersection of its __________.
(d) The number 3 has a __________ line of symmetry.
(e) A line of symmetry is also called a __________.
Answers:
(a) All objects have rotational symmetry of order 1.
(b) An icecream cone has 1 line of symmetry.
(c) Centre of rotation of a square lies at the point of intersection of its diagonals.
(d) The number 3 has a horizontal line of symmetry.
(e) A line of symmetry is also called a mirror line.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 12 Symmetry:
Our team of Indian and foreign educated engineers have scientifically crafted these solutions on symmetry, taking into account every detail and presenting them in the most easy-to-understand way possible. Every single problem has been worked out in detail, along with attractive figures and clear explanations, wherever possible. We recommend that you go through them in detail to extract maximum benefit from them.
Feel free to download the free PDFs of the solutions anytime! There’s plenty more helpful study material and other resources on the way – so keep visiting our website and join our email list to get free access to them!
The main topics covered are:
12.1 – Introduction
12.2 – Lines of Symmetry for Regular Polygons
12.3 – Rotational Symmetry
12.4 – Line Symmetry and Rotational Symmetry
Here are the number of problems by each chapter:
Exercise 11.1 – 8 questions
Exercise 11.2 – 5 questions
Exercise 11.3 – 4 questions
To master this chapter you will need to learn how to carefully examine figures, study them in different orientations and be able to make the right conclusions. For this we recommend that you practise drawing the figures in different orientations and try to accurately identify the lines of symmetry, rotational symmetry etc.
We recommend you draw the appropriate figures and try to arrive at the solutions yourselves, alongside looking at the solutions. This chapter involves a lot of hands-on drawing of figures – so make sure you learn how to draw them and interpret them.
To correctly identify the different types of symmetry, you will need a trained eye. This will only come with hands-on practice. Once you start drawing out the figures yourself and studying them in detail, your ability to correctly identify the types of symmetry will increase. Practise as many problems as you can to be able to answer questions quickly in your exams.
At educationroundtheworld.com, our expert teacher-mentors provide excellent coaching and mentoring as well at no extra cost. Contact us anytime with your requirements and let us help you out.
At educationroundtheworld.com we follow a teacher-mentor approach for all-round development of students. In addition to systematic and structured teaching, we mentor students and make them aware of their talents and opportunities that lie ahead. We provide the mentoring at no extra cost, which is even more beneficial. If that is what you want, feel free to contact us anytime. We provide on-demand one-to-one coaching, based on your convenience and your needs – have it completely your way! Book any number of live online classes now!


