Hello guys! Looking for help with your geometry? We have carefully prepared these Chapter 5 Lines and Angles solutions to help beginners quickly grasp the concepts and problem-solving techniques. We have also included some typical extra problems which will further clear your concepts and give you practice. Please go ahead and look through them – we are confident you find them useful.
Solutions to Exercise 5.1 (Page No 77) of NCERT Class 7 Math 5 Lines and Angles –
1. Find the complement of each of the following angles:
(i)
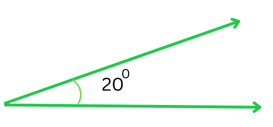
Answer:
Two angles are complementary when the sum of their measures = 900.
The above angle = 200.
Let the measure of its complement be x0.
Therefore we get,
x + 200 = 900
or, x = 900 – 200
or, x = 700 (This is the complement of the given angle)
(ii)

Answer:
Two angles are complementary when the sum of their measures = 900.
The above angle = 630.
Let the measure of its complement be x0.
Therefore we get,
x + 630 = 900
or, x = 900 – 630
or, x = 270 (This is the complement of the given angle)
(iii)
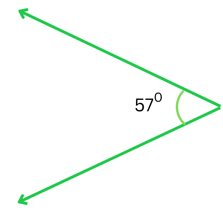
Answer:
Two angles are complementary when the sum of their measures = 900.
The above angle = 570.
Let the measure of its complement be x0.
Therefore we get,
x + 570 = 900
or, x = 900 – 570 or, x = 330 (This is the complement of the given angle)
2. Find the supplement of each of the following angles
(i)
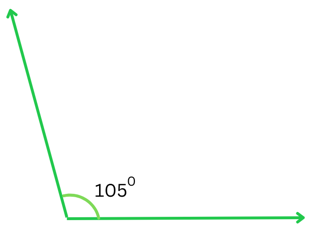
Answer:
Two angles are supplementary when the sum of their measures = 1800.
The above angle = 1050.
Let the measure of its supplement be x0.
Therefore we get,
x + 1050 = 1800
or, x = 1800 – 1050
or, x = 750 (This is the supplement of the given angle)
(ii)
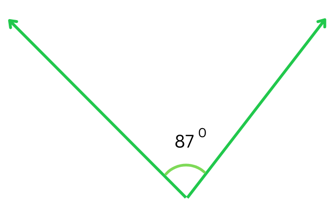
Answer:
Two angles are supplementary when the sum of their measures = 1800.
The above angle = 870.
Let the measure of its supplement be x0.
Therefore we get,
x + 870 = 1800
or, x = 1800 – 870
or, x = 930 (This is the supplement of the given angle)
(iii)

Answer:
Two angles are supplementary when the sum of their measures = 1800.
The above angle = 1540.
Let the measure of its supplement be x0.
Therefore we get,
x + 1540 = 1800
or, x = 1800 – 1540 or, x = 260 (This is the supplement of the given angle)
3. Identify which of the following pairs of angles are complementary and which are supplementary.
(i) 650, 1150
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 650 + 1150 = 1800
When the sum of the measures of the two angles = 1800, they are said to be supplementary.
Therefore, we conclude that the above angles are supplementary.
(ii) 630, 270
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 630 + 270 = 900
When the sum of the measures of the two angles = 900, they are said to be complementary.
Therefore, we conclude that the above angles are complementary.
(iii) 1120, 680
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 1120 + 680 = 1800
When the sum of the measures of the two angles = 1800, they are said to be supplementary.
Therefore, we conclude that the above angles are supplementary.
(iv) 1300, 500
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 1300 + 500 = 1800
When the sum of the measures of the two angles = 1800, they are said to be supplementary.
Therefore, we conclude that the above angles are supplementary.
(v) 450, 450
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 450 + 450 = 900
When the sum of the measures of the two angles = 900, they are said to be complementary.
Therefore, we conclude that the above angles are complementary.
(vi) 800, 100
Answer:
We proceed to take the sum of the given angles and use that to make our conclusions.
So, 800 + 100 = 900
When the sum of the measures of the two angles = 900, they are said to be complementary. Therefore, we conclude that the above angles are complementary.
4. Find the angle which is equal to its complement.
Answer:
Let the measure of the unknown angle be x0. So, the complement in this case is also x0.
Two angles are said to be complementary when the sum of their measures = 900.
Therefore,
x0 + x0 = 900
or, 2x0 = 900
or, x0 = 90/2 = 450
So, the required angle which is equal to its complement = 450.
5. Find the angle which is equal to its supplement.
Answer:
Let the measure of the unknown angle be x0. So, the supplement in this case is also x0.
Two angles are said to be supplementary when the sum of their measures = 1800.
Therefore,
x0 + x0 = 1800
or, 2x0 = 1800
or, x0 = 180/2 = 900
So, the required angle which is equal to its supplement = 900.
6. In the given figure, ∠1 and ∠2 are supplementary angles.
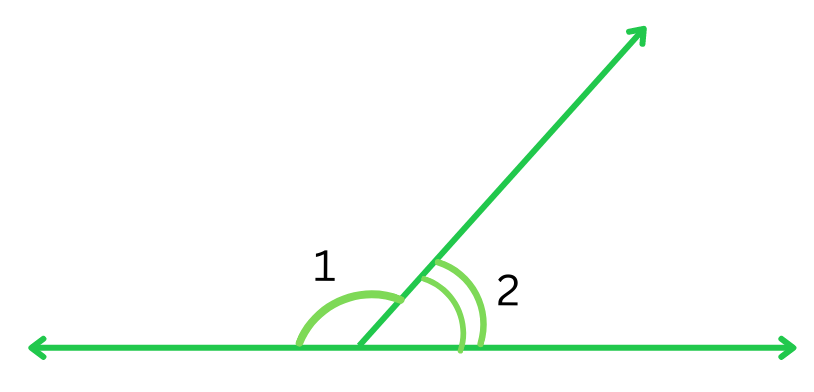
If ∠1 is decreased, what changes should take place in ∠2 so that both angles still remain supplementary?
Answer:
Two angles are said to be supplementary when the sum of their measures = 1800.
So, ∠1 + ∠2 = 1800.
Let ∠1 be decreased by x0.
Therefore, the measure of new ∠1 = (∠1 – x)0.
Therefore, for the new angles to remain supplementary, the measure of new ∠2 will have to be (∠2 + x)0 to keep the sum = 1800:
(∠1 – x) + (∠2 + x) = 1800 (Since we know ∠1 + ∠2 = 1800) Therefore, ∠2 will have to increase.
7. Can two angles be supplementary if both of them are:
(i) acute?
Answer:
An acute angle is less than 900.
If both angles are acute (that is, less than 900), then their sum will always be less than 1800. Therefore, they will not be supplementary.
We encourage you to take different values for the acute angles and see for yourself that this is true!
(ii) obtuse?
Answer:
An obtuse angle will always be greater than 900.
If both angles are obtuse (that is, more than 900), then their sum will always be more than 1800. Therefore, they will not be supplementary.
Take different values for the obtuse angles and convince yourself that this is true!
(iii) right?
Answer:
The measure of one right angle = 900.
If both angles are right (= 900), then their sum = 900 + 900 = 1800. Therefore, they will be supplementary.
8. An angle is greater than 450. Is its complementary angle greater than 450 or equal to 450 or less than 450?
Answer:
Let the angle be greater than 450 by x0. So, the angle = (45 + x)0.
Two angles are said to be complementary when the sum of their measures = 900.
Therefore, the complementary angle will have to be = (45 – x)0 to keep the sum = 900 as we can see below:
(45 + x)0 + (45 – x)0 = 900. Therefore, the measure of the complementary angle = (45 – x)0 which is less than 450.
9. Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is _______.
Answer:
If two angles are complementary, then the sum of their measures is 900.
(ii) If two angles are supplementary, then the sum of their measures is ______.
Answer:
If two angles are supplementary, then the sum of their measures is 1800.
(iii) Two angles forming a linear pair are _______________.
Answer:
Two angles forming a linear pair are supplementary.
(iv) If two adjacent angles are supplementary, they form a ___________.
Answer:
If two adjacent angles are supplementary, they form a linear pair.
(v) If two lines intersect at a point, then the vertically opposite angles are always
_____________.
Answer: If two lines intersect at a point, then the vertically opposite angles are always equal.
10. In the adjoining figure, name the following pairs of angles.
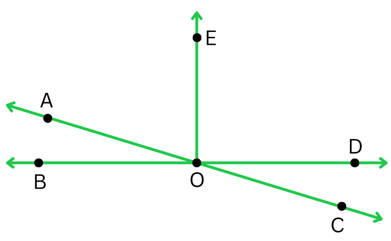
(i) Obtuse vertically opposite angles
Answer:
Obtuse angles will be greater than 900. Therefore, the obtuse vertically opposite angles in the above figure are ∠AOD and ∠BOC.
(ii) Adjacent complementary angles
Answer:
The adjacent complementary angles in the above figure are ∠EOA and ∠AOB (They have a common vertex O and a common arm OA, and it is easy to see that the non-common arms OB and OE lie on either side of the common arm. Also, it is easy to see that ∠EOA + ∠AOB = 900).
(iii) Equal supplementary angles
Answer:
∠EOB and ∠EOD are both = 900 and their sum = 1800. Therefore, they are equal supplementary angles.
(iv) Unequal supplementary angles
Answer:
∠EOA and ∠EOC are unequal supplementary angles because they are not equal and their sum = 1800.
(v) Adjacent angles that do not form a linear pair
Answer:
∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are adjacent angles that do not form a linear pair.
Solutions to Exercise 5.2 (Page No 86) of NCERT Class 7 Math Chapter 5 Lines and Angles –
1. State the property that is used in each of the following statements?
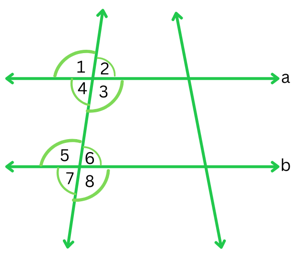
(i) If a ∥ b, then ∠1 = ∠5.
Answer:
The property that corresponding angles are equal is used in the above statement.
(ii) If ∠4 = ∠6, then a ∥ b.
Answer:
The property that if alternate interior angles are equal, then the lines will be parallel is used in the above statement.
(iii) If ∠4 + ∠5 = 1800, then a ∥ b.
Answer:
The property that if a pair of interior angles on the same side of the transversal are supplementary, then the lines will be parallel is used in the above statement.
2. In the adjoining figure, identify
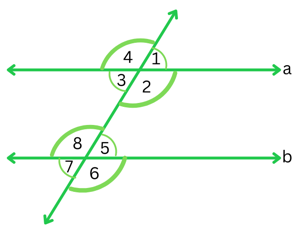
(i) the pairs of corresponding angles.
Answer:
The pairs of corresponding angles are: ∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7 (they have different vertices, are on the same side of the transversal and are in corresponding positions – above or below, left or right – relative to the two lines).
(ii) the pairs of alternate interior angles.
Answer:
Two pairs of alternate interior angles are: ∠2 and ∠8, ∠3 and ∠5.
(iii) the pairs of interior angles on the same side of the transversal.
Answer:
The pairs of interior angles on the same side of the transversal are:∠2 and ∠5, ∠3 and ∠8.
(iv) the vertically opposite angles.
Answer:
The vertically opposite angles are: ∠1 and ∠3, ∠4 and ∠2, ∠5 and ∠7, ∠8 and ∠6.
3. In the adjoining figure, p ∥ q. Find the unknown angles.
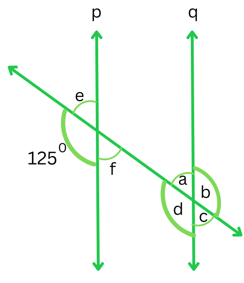
Answer:
We can see that 1250 and ∠e is a linear pair.
Therefore,
1250 + e = 1800
or, e = 1800 – 1250
or, ∠e = 550
Also, ∠e and ∠f are equal, being vertically opposite angles.
Therefore,
∠f = ∠e = 550
Now, ∠d and 1250 are corresponding angles, p and q being parallel lines.
Therefore,
∠d = 1250
∠d and ∠b are equal, being vertically opposite angles.
Therefore,
∠b = ∠d = 1250
Now, ∠a and ∠e are corresponding angles, p and q being parallel lines.
Therefore,
∠a = ∠e = 550
∠a and ∠c are equal, being vertically opposite angles.
∠c = 550
The unknown angles are: ∠e = 550, ∠f = 550, ∠b = 1250, ∠d = 1250, ∠a = 550, ∠c = 550
4. Find the value of x in each of the following figures if l ∥ m.
(i)
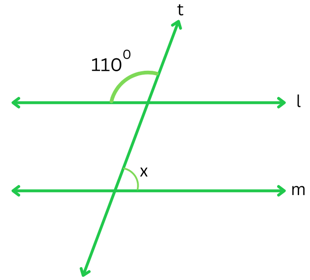
Answer:
We take the angle on the other side of line t as ∠y (as shown in the figure below):

We can see that 1100 and ∠y are a linear pair.
Therefore,
1100 + y = 1800
or, y = 1800 – 1100
or, ∠y = 700
Now, ∠y and ∠x are corresponding angles because lines l and m are parallel.
Therefore,
∠x = ∠y = 700
(ii)
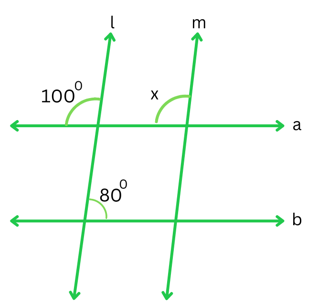
Answer:
1000 and ∠x are corresponding angles because lines l and m are parallel.
Therefore, ∠x = 1000
5. In the given figure, the arms of two angles are parallel.
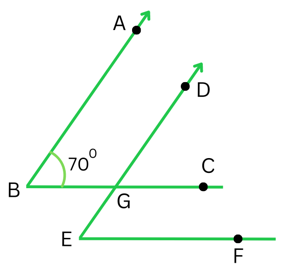
If ∠ABC = 700, then find
(i) ∠DGC
(ii) ∠DEF
Answer:
(i) It is given that the arms of the two angles are parallel, AB ∥ DE and BC is the transversal.
Therefore,
∠DGC = ∠ABC (being corresponding angles)
or, ∠DGC = 700
Again, since it is given that the arms of the two angles are parallel, BC ∥ EF and DE is the transversal.
Therefore,
∠DEF = ∠DGC (being corresponding angles) or, ∠DEF = 700
6. In the given figures below, decide whether l is parallel to m.
Answer:
(i) The figure is shown below:
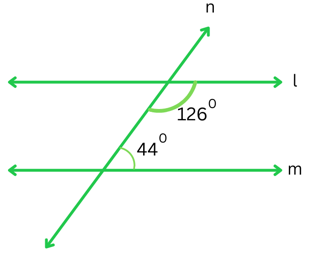
The transversal n cuts the lines l and m.
The sum of the interior angles on the same side of the transversal = 1260 + 440 = 1700.
The sum ≠ 1800, therefore interior angles on the same side of the transversal are not supplementary and the lines l and m are not parallel.
(ii) The figure is shown below:
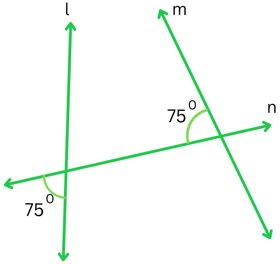
Let the vertically opposite angle formed by the intersection of the lines l and n be x (as shown below):

Since, vertically opposite angles are equal,
x = 750
The transversal n cuts the lines l and m.
The sum of the interior angles on the same side of the transversal = 750 + 750 = 1500.
The sum ≠ 1800, therefore interior angles on the same side of the transversal are not supplementary and the lines l and m are not parallel.
(iii) The figure is shown below:

Let x be the angle which is the supplement of the angle 1230 on the other side of n (as shown below):
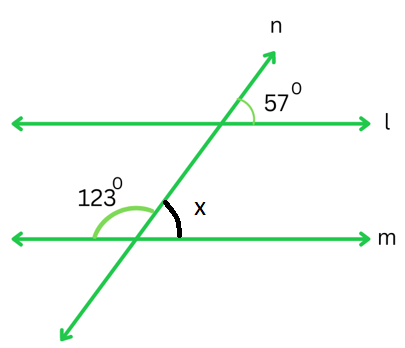
Therefore,
1230 + x = 1800
or, x = 1800 – 1230
or, x = 570
We can see that the corresponding angles 570 (given) and x (which we also found to be = 570) are equal.
Therefore, the lines l and m are parallel.
(iv) The figure is shown below:
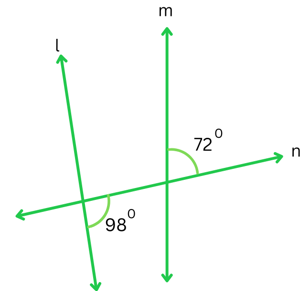
Let x be the angle which is the supplement of the angle 980 on the other side of n (as shown below):
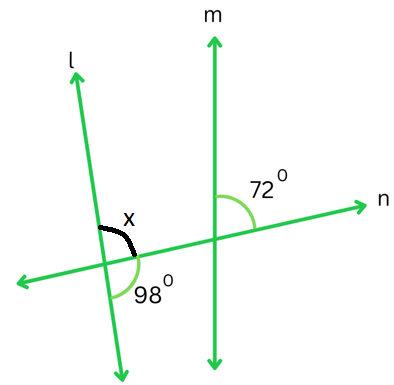
Therefore,
980 + x = 1800
or, x = 1800 – 980
or, x = 820
We can see that the corresponding angles 720 (given) and x (which we also found to be = 820) are not equal.
Therefore, the lines l and m are not parallel.
Important Questions from Previous NCERT Textbook:
Exercise 5.1 Page No: 101 (Old Textbook):
9. In the adjoining figure:

(i) Is ∠1 adjacent to ∠2?
Answer:
Yes ∠1 is adjacent to ∠2 because:
- They have a common vertex O.
- They have a common arm OC
- The non-common arms OA and OE are on either side of the common arm OC.
(ii) Is ∠AOC adjacent to ∠AOE?
Answer:
No AOC is not adjacent to ∠AOE because:
Although they have a common vertex O and a common arm OA, it is easy to see that the non-common arms OC and OE do not lie on either side of the common arm.
(iii) Do ∠COE and ∠EOD form a linear pair?
Answer:
Yes, ∠COE and ∠EOD form a linear pair because:
- They are adjacent angles with common vertex O, a common arm OE and the non-common arms OC and OD on either side of the of the common arm OE.
- Also, the non-common sides OC and OD are opposite rays.
(iv) Are ∠BOD and ∠DOA supplementary?
Answer:
∠BOD and ∠DOA lie on the same line AB on either side of the common arm OD and so, we can say that ∠BOD + ∠DOA = 1800. Therefore, they are supplementary.
(v) Is ∠1 vertically opposite to ∠4?
Answer:
Yes ∠1 vertically opposite to ∠4 as they are formed by the intersection of the straight lines AB and CD and are opposite to each other.
(vi) What is the vertically opposite angle of ∠5?
Answer: The vertically opposite angle of ∠5 (that is ∠AOD) is ∠COB as they are formed by the intersection of the straight lines AB and CD and are opposite to each other.
10. Indicate which pairs of angles are:
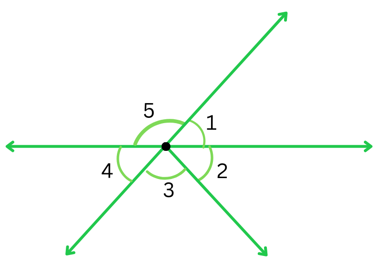
(i) Vertically opposite angles.
Answer:
Vertically opposite angles are formed by the intersection of two straight lines and are opposite to each other.
Therefore, in the above figure, ∠1 and ∠4 is one pair of vertically opposite angles because they are formed by the intersection of two straight lines and are opposite to each other.
Also, ∠5 and ∠(3 + 2) is another pair of vertically opposite angles as they are formed by the intersection of the same two straight lines and are opposite to each other.
(ii) Linear pairs.
Answer:
A linear pair is a pair of adjacent angles whose non-common sides are opposite rays.
Therefore, we find the following pairs of linear angles in the above figure:
- ∠1 and ∠5
- ∠5 and ∠4
- ∠3 and ∠(1 + 2)
- ∠1 and ∠(3 + 2)
11. In the following figure, is ∠1 adjacent to ∠2? Give reasons.

Answer:
The angles ∠1 and ∠2 are not adjacent to each other as they do not have a common vertex.
12. Find the values of the angles x, y, and z in each of the following:
(i)

Answer:
x and 550 are vertically opposite angles formed by the intersection of two lines and are equal to each other.
Therefore, x = 550.
Also, we can see that 550 and y are a linear pair.
Therefore,
550 + y = 1800
or, y = 1800 – 550
or, y = 1250
Now, y and z are vertically opposite angles and are equal to each other.
Therefore,
z = y = 1250
(ii)

Answer:
z and 400 are vertically opposite angles formed by the intersection of two lines and are equal to each other.
Therefore, z = 400.
Also, we can see that 400 and y are a linear pair.
Therefore,
400 + y = 1800
or, y = 1800 – 400
or, y = 1400
Also, we can say that:
400 + x + 250 = 1800 [Since they are angles on the same side of a straight line]
or, x + 650 = 1800
or, x = 1800 – 650 or, x = 1150
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 5 Lines and Angles:
Very Short Answer Type Questions:
1. You are given two angles 750 and 150. Are they complementary?
Answer:
Sum of the two angles = 750 + 150 = 900. Therefore, they are complementary.
2. When does an adjacent angle become a linear pair?
Answer:
Adjacent angles become a linear pair when their non-common sides are opposite rays.
3. ∠A = ∠B = 550. They can be: (i) Supplementary angles or (ii) Vertically opposite angles or (iii) both – which one is true?
Answer:
They can be (ii) Verticallyopposite angles.
4. Suppose two lines are given. How many transversals can you draw for these lines?
Answer:
You can draw infinitely many transversals.
5. A transversal cuts a pair of lines and the alternate angles are equal. What can be said about the corresponding angles?
Answer:
Since the alternate angles are equal, the lines are parallel. Therefore, the corresponding angles are equal.
6. Two lines intersect each other and the values of all the angles are equal. What can be we say about the value of each?
Answer:
Value of each = 3600/4 = 900.
7. Prove that the opposite sides of a square are parallel.
Answer:
Sum of each pair of interior angles on the same side of the transversal = 900 + 900 = 1800. Therefore, the opposite sides are parallel to each other.
8. Do two lines always intersect each other at one point?
Answer:
No, two parallel lines do not intersect each other at all.
9. Can two acute angles form a linear pair?
Answer:
No, two acute angles cannot form a linear pair. To form a linear pair, if one angle is acute the other angle will be obtuse.
10. What do we call two right angles which are adjacent to each other?
Answer:
They form a linear pair.
Short and Long Answer Type Questions:
1. Two angles are supplementary and one is thrice the other. What are their values?
Answer:
Let the smaller angle be x.
The bigger angle be 3x
Therefore,
x + 3x = 1800
or, 4x = 1800
or, x = 180/4
or, x = 450
3x = 450 × 3 = 1350 Therefore, the values of the angles are 450 and 1350.
2. In the figure below ∠ AOB = 250 and ∠ AOP = ∠ BOQ. Find the value of each.

Answer:
We have,
∠ AOP + ∠ AOB + ∠ BOQ = 1800
or, ∠ AOP + 250 + ∠ BOQ = 1800
or, ∠ AOP + ∠ BOQ = 1800 – 250 = 1550
or, 2∠ AOP = 1550 (Since ∠ AOP = ∠ BOQ)
or, ∠ AOP = 155/2
or, ∠ AOP = 77.50 Therefore, ∠ AOP = ∠ BOQ = 77.50.
3. In the figure below ∠ AOP = 400 and ∠ROS = 800. Find the value of ∠ BOQ.
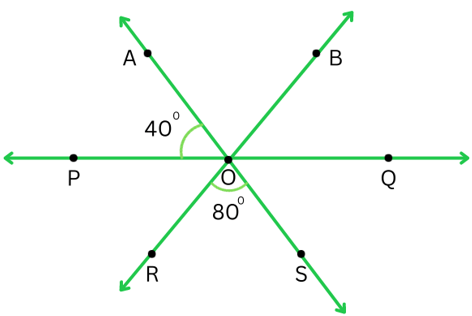
Answer:
We have,
∠ AOB = ∠ROS = 800 (vertically opposite angles)
Now,
∠ AOP + ∠ AOB + ∠ BOQ = 1800
or, 400 + 800 + ∠ BOQ = 1800
or, 1200 + ∠ BOQ = 1800
or, ∠ BOQ = 1800 – 1200 or, ∠ BOQ = 600 (Answer)
4. In the figure below ∠ AXQ = 600 and ∠RYX = 1100. Verify if the lines PQ and RS are parallel.
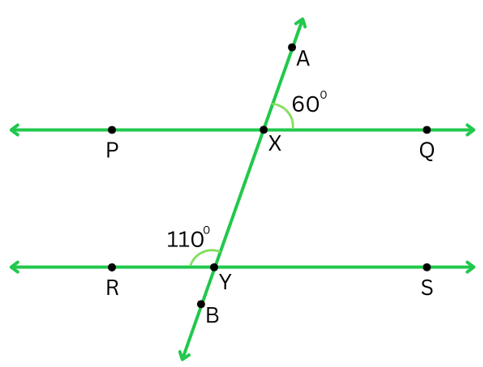
Answer:
We have,
∠ AXQ = ∠ PXY = 600 (Vertically opposite angles)
Now,
∠ PXY and ∠RYX are pairs of interior angles on the same side of the transversal.
We have,
∠ PXY + ∠RYX = 600 + 1100 = 1700 For the lines PQ and RSto be parallel ∠ PXY + ∠RYX must be equal to 1800.
Therefore, we conclude the lines PQ and RS are not parallel.
5. In the figure below identify which lines are parallel to each other.
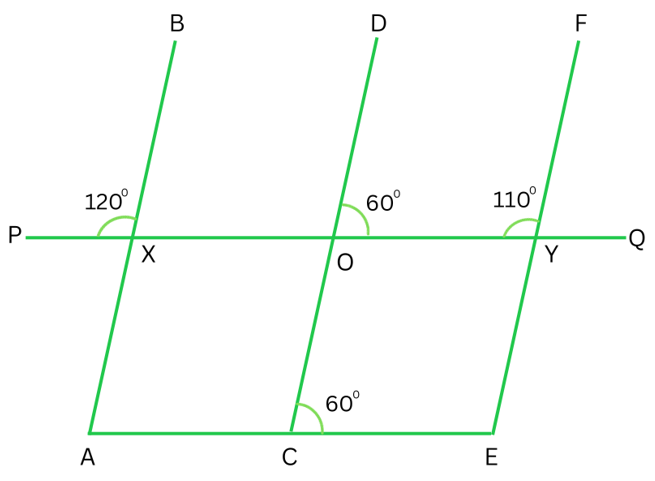
Answer:
∠ BXP + ∠ BXO = 1800
or, 1200 + ∠ BXO = 1800
or, ∠ BXO = 1800 – 1200
or, ∠ BXO = 600
We can see that between lines AB and CD, PQ is the transversal and corresponding angles ∠ BXO = ∠ DOY = 600.
Therefore, AB || CD.
Again, we have ∠ DOY + ∠FYO = 600 + 1100 = 1700. Since sum of interior angles on the same side of the transversal is not equal to 1800, we conclude that DO and FY are not parallel.
Now again CD is the transversal and corresponding angles ∠ DOY = ∠ DCE = 600. Therefore, we conclude PQ is parallel to AE.
6. In the figure below PQ || RS. Identify what kind of triangle Δ ABC is.
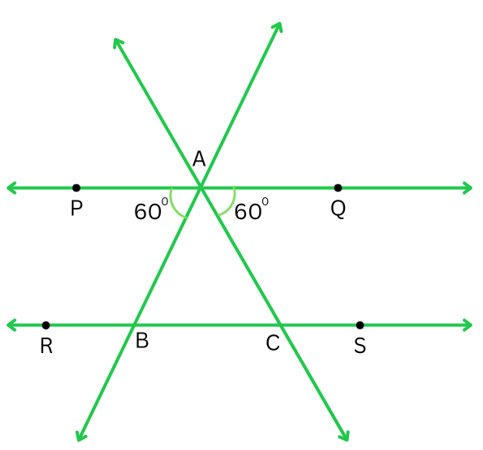
Answer:
Since PQ || RS,
∠ PAB = ∠ ABC (Alternate angles)
So, ∠ ABC = 600
Also,
∠ QAC = ∠ ACB (Alternate angles)
So, ∠ ACB = 600
In Δ ABC,
∠ ABC + ∠ ACB + ∠ BAC = 1800
or, 600 + 600 + ∠ BAC = 1800
or, 1200 + ∠ BAC = 1800
or, ∠ BAC = 1800 – 1200
or, ∠ BAC = 600
All three angles of Δ ABC are equal. Therefore, Δ ABC is equilateral triangle.
7. In an equilateral triangle one side is extended. What is the value of the adjacent angle thus formed?
Answer:
Each angle of an equilateral triangle = 600.
When one side is produced, the adjacent angle forms a linear pair with the 600 angle.
Therefore, Adjacent angle = 1800 – 600 = 1200
8. We are given that (2a + 30)0 = 600. What is the relation between (2a + 30)0 and (a + 15)0?
Answer:
We have,
2a + 30 = 60
or, 2a = 60 – 30
or, 2a = 30
or a = 30/2 = 150
(a + 15)0 = (15 + 15)0 = 300
Now, (2a + 30)0 + (a + 15)0 = 600 + 300 = 900
Therefore, (2a + 30)0 and (a + 15)0 are complementary.
Fill in the Blanks:
(a) The angles 2x and 1800 – 2x are __________.
(b) If two angles are supplementary and one angle is acute, then the other angle is __________.
(c) In a right-angled triangle the two angles other than the right angle are __________.
(d) When two lines intersect each other the vertically opposite angles are complementary. The lines are __________ to each other.
(e) If a transversal intersects two parallel lines, alternate interior angles have one common __________.
Answers:
(a) The angles 2x and 1800 – 2x are supplementary.
(b) If two angles are supplementary and one angle is acute, then the other angle is obtuse.
(c) In a right-angled triangle the two angles other than the right angle are complementary.
(d) When two lines intersect each other the vertically opposite angles are complementary. The lines are perpendicular to each other.
(e) If a transversal intersects two parallel lines, alternate interior angles have one common arm.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 5 Lines and Angles:
These solutions have been prepared by Indian and foreign educated engineers and scientists, who have vast experience in teaching students of all levels. They understand your needs and have designed the solutions in a way that is easy for beginners to understand. They have even included a set of extra problems for you to practise. If you look at the solutions carefully, you should be able to grasp the concepts quickly.
Also, you are welcome to download the solutions for free anytime. We are always working to provide you with the best study material and resources, so keep visiting our website subscribe our email list to get free and immediate access to them!
The main topics covered are:
5.1 – Introduction
5.2 – Related Angles
5.3 – Pairs of Lines
5.4 – Checking for Parallel Lines
Here are the number of problems by each chapter:
Exercise 5.1 – 10 questions
Exercise 5.2 – 6 questions
Yes indeed! You can download the free PDFs of the solutions (please look towards the top of the page) and use them for practice!
Two lines can intersect at only one point.
No, parallel lines do not intersect each other.
Angles are used by carpenters to obtain precise measurements when making doors, furniture etc. Angles find vast applications in engineering and the sciences for making precise calculations.
The most important part of this chapter is applying the different concepts individually or in combination with one another to solve problems. The challenge lies in identifying the right techniques needed to get to the solution. This will come with sufficient practice. We recommend regular practice, so you don’t forget the concepts. Not only will this help you ace your exams, they also prepare you for the geometry topics in higher classes. You will find that with enough practice, the concepts and techniques will become like second nature to you.
Our solutions material is an excellent place to start. We suggest that you try to solve the problems on your own, alongside looking at our solutions. In geometry, there might be multiple ways to solve a problem. Try to come up with alternative methods of solving the problems that are not given in the solutions. This will further clear your concepts and give you confidence.
And of course, if you need any extra help, we are there for you! Reach out to us anytime with your requirements!
9. What if I need additional help beyond your solutions?
Our expert teacher-mentors will be there to coach you and mentor you anytime. Expert teaching combined with the right kind of mentoring will give you confidence regarding your future. If that is what you are looking for, feel free to reach out to us anytime with your requirements. We provide top-quality one-to-one coaching and mentoring, based on your convenience and your needs – have it completely your way! Book an appointment now!


