Solutions to NCERT Class 7 Math Chapter 6 The Triangle and its Properties:

Hello students! Feel free to go through our solutions to Chapter 6 The Triangle and its Properties right here. They have been scientifically prepared and you should be able to grasp the concepts quickly. We have also provided extra sample problems of many formats which will give you extra practice. We’re only getting started posting top-quality material for you and there’s plenty more on the way. So keep visiting and keep studying!

Solutions to Exercise 6.1 (Page No 91) of NCERT Class 7 Math Chapter 6 The Triangle and its Properties –

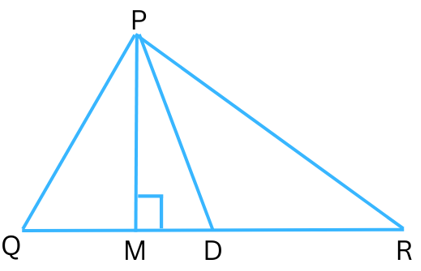
1. In Δ PQR, D is the mid-point of QR.

Answer:

PM is altitude.

The altitude is the shortest distance between the vertex P and the side QR which is opposite to P. Here it is easy to see that the altitude is PM.

PD is median.

The line segment PD joins D, which is the mid-point of QR, to its opposite vertex P. Therefore, PD is the median.

Is QM = MR?

No, QM is not equal to MR, because M is not the mid-point of QR (the mid-point is D).

2. Draw rough sketches for the following:

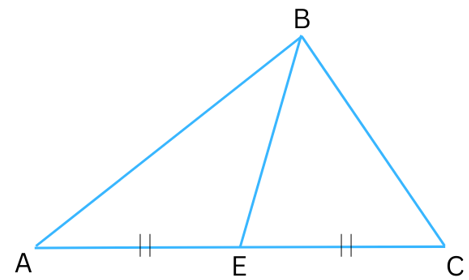
(a) In ΔABC, BE is a median.

Answer: In the figure below. BE is the median and AE = EC.

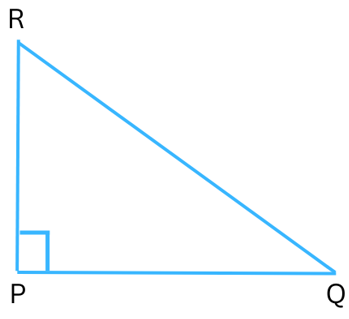
(b) In ΔPQR, PQ and PR are altitudes of the triangle.

Answer: In the figure,RP is one altitude (shortest distance between the vertex R and the side PQ) and PQ is another altitude (shortest distance between the vertex Q and the side RP).

(c) In ΔXYZ, YL is an altitude in the exterior of the triangle.

Answer: YL is the altitude in the exterior of ΔXYZ (YL is the shortest distance between the vertex Y and the line LZ formed by extending side ZX).

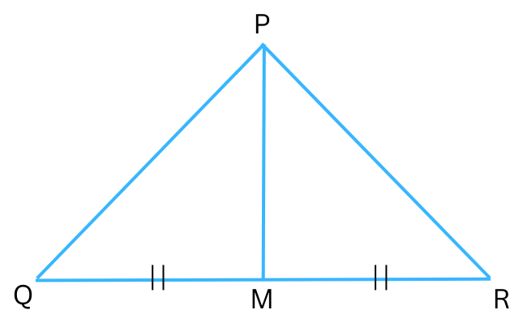
3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be the same.

Answer: In the isosceles triangle ΔPQR, PQ = PR. Draw the altitude PM of the triangle. You will notice that if you measure QM and MR with a ruler, length of QM will be = length of MR. So M is the point of QR and therefore, we conclude that PM is also the median.

Solutions to Exercise 6.2 (Page No 93) of NCERT Class 7 Math Chapter 6 The Triangle and its Properties –

1. Find the value of the unknown exterior angle x in the following diagram:

(i)

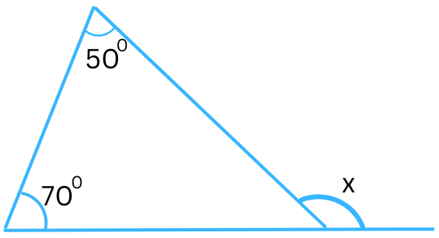
Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 50⁰ and 70⁰.

Therefore,

x = 50⁰ + 70⁰ = 120⁰

(ii)

Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 65⁰ and 45⁰.

Therefore,

x = 65⁰ + 45⁰ = 110⁰

(iii)

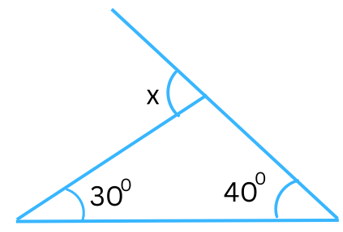
Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 30⁰ and 40⁰.

Therefore,

x = 30⁰ + 40⁰ = 70⁰

(iv)

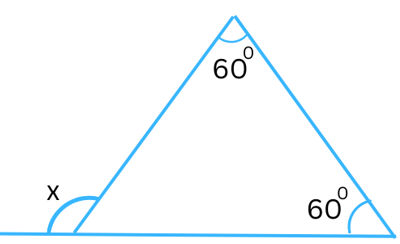
Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 60⁰ and 60⁰.

Therefore,

x = 60⁰ + 60⁰ = 120⁰

(v)

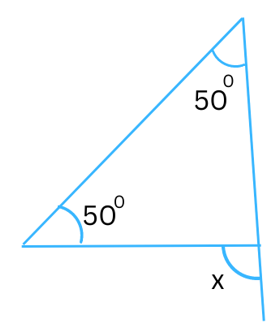
Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 50⁰ and 50⁰.

Therefore,

x = 50⁰ + 50⁰ = 100⁰

(vi)

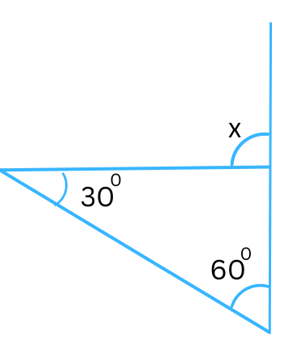
Answer:

The exterior angle = sum of the interior opposite angles.

In the above triangle the exterior angle is x and the interior opposite angles are 30⁰ and 60⁰.

Therefore, x = 30⁰ + 60⁰ = 90⁰

2. Find the value of the unknown interior angle x in the following figures:

(i)

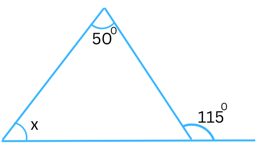
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 115⁰ and the interior opposite angles are x and 50⁰.

Therefore,

x + 50⁰ = 115⁰

or, x = 65⁰

(ii)

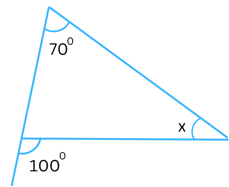
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 100⁰ and the interior opposite angles are x and 70⁰.

Therefore,

x + 70⁰ = 100⁰

or, x = 100⁰ – 70⁰ 

or, x = 30⁰ 

(iii)

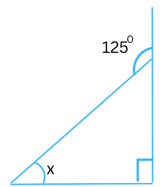
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 125⁰ and the interior opposite angles are x and 90⁰.

Therefore,

x + 90⁰ = 125⁰

or, x = 125⁰ – 90⁰ 

or, x = 35⁰

(iv)

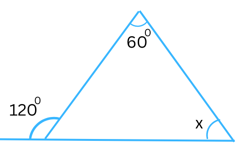
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 120⁰ and the interior opposite angles are x and 60⁰.

Therefore,

x + 60⁰ = 120⁰

or, x = 120⁰ – 60⁰ 

or, x = 60⁰

(v)

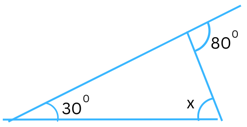
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 80⁰ and the interior opposite angles are x and 30⁰.

Therefore,

x + 30⁰ = 80⁰

or, x = 80⁰ – 30⁰ 

or, x = 50⁰

(vi)

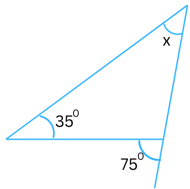
Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 75⁰ and the interior opposite angles are x and 35⁰.

Therefore,

x + 35⁰ = 75⁰

or, x = 75⁰ – 35⁰ 

or, x = 40⁰

Solutions to Exercise 6.3 (Page No 96) of NCERT Class 7 Math Chapter 6 The Triangle and its Properties –

1. Find the value of the unknown x in the following diagrams:

(i)

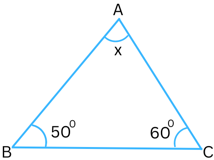
Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

∠ABC + ∠ACB + ∠BAC = 180⁰

It is given that ∠ABC = 50⁰ and ∠ACB = 60⁰.

So, 50⁰ + 60⁰ + x = 180⁰

or, 110⁰ + x = 180⁰

or, x = 180⁰ – 110⁰

or, x = 70⁰

(ii)

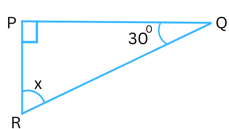
Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

∠QPR + ∠PRQ + ∠PQR = 180⁰

It is given that ∠QPR = 90⁰ and ∠PQR = 30⁰.

So, 90⁰ + 30⁰ + x = 180⁰

or, 120⁰ + x = 180⁰

or, x = 180⁰ – 120⁰

or, x = 60⁰

(iii)

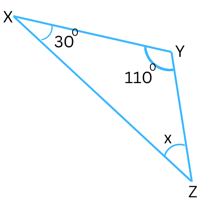
Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

∠YXZ + ∠YZX + ∠XYZ = 180⁰

It is given that ∠YXZ = 30⁰ and ∠XYZ = 110⁰.

So, 30⁰ + ∠YZX + 110⁰ = 180⁰

or, 140⁰ + x = 180⁰

or, x = 180⁰ – 140⁰

or, x = 40⁰

(iv)

Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

x + x + 50⁰ = 180⁰

or, 2x = 180⁰ – 50⁰

or, 2x = 130⁰

or, x = 130/2 = 65⁰

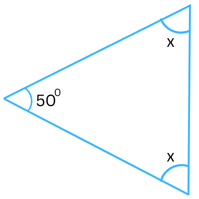
(v)

Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

x + x + x = 180⁰

or, 3x = 180⁰

or, 3x = 180⁰

or, x = 180/3 (Dividing both sides by 3)

= 60⁰

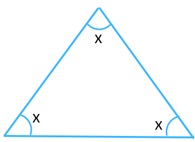
(vi)

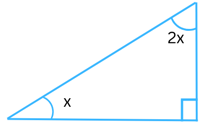
Answer:

The sum of the interior angles in a triangle always = 180⁰.

Therefore,

x + 2x + 90⁰ = 180⁰

or, 3x = 180⁰ – 90⁰

or, 3x = 90⁰

or, x = 90/3 (Dividing both sides by 3)

= 30⁰ and 2x = 2 × 30⁰ = 60⁰

2. Find the values of the unknowns x and y in the following diagrams:

(i)

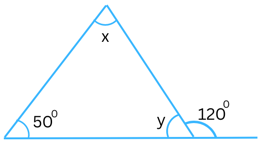
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is 120⁰ and the interior opposite angles are x and 50⁰.

So,

x + 50⁰ = 120⁰

or, x = 120⁰ – 50⁰

or, x = 70⁰

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

x + y + 50⁰ = 180⁰

or, 70⁰ + y + 50⁰ = 180⁰

or, y + 120⁰ = 180⁰

or, y = 180⁰ – 120⁰

or, y = 60⁰

(ii)

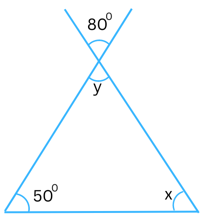
Answer:

We know that vertically opposite angles are equal.

So, y = 80⁰.

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

x + y + 50⁰ = 180⁰

or, x + 80⁰ + 50⁰ = 180⁰

or, x + 130⁰ = 180⁰

or, x = 180⁰ – 130⁰

or, x = 50⁰

(iii)

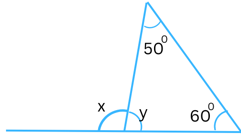
Answer:

Sum of the interior opposite angles = the exterior angle

In the above triangle the exterior angle is x and the interior opposite angles are 50⁰ and 60⁰.

So,

x = 50⁰ + 60⁰

or, x = 110⁰

or, x = 110⁰

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

y + 50⁰ + 60⁰ = 180⁰

or, y + 110⁰ = 180⁰

or, y = 180⁰ – 110⁰

or, y = 180⁰ – 110⁰

or, y = 70⁰

(iv)

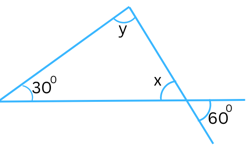
Answer:

We know that vertically opposite angles are equal.

So, x = 60⁰.

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

x + y + 30⁰ = 180⁰

or, 60⁰ + y + 30⁰ = 180⁰

or, y + 90⁰ = 180⁰

or, y = 180⁰ – 90⁰

or, y = 90⁰

(v)

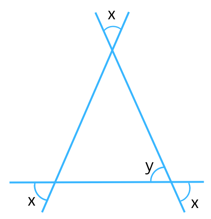
Answer:

We know that vertically opposite angles are equal.

So, in the triangle: y = x and the other two angles are both = x.

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

x + x + x = 180⁰

or, 3x = 180⁰

or, x = 180/3 (Dividing both sides by 3)

or, x = 60⁰

Solutions to Exercise 6.4 (Page No 101) of NCERT Class 7 Math Chapter 6 The Triangle and its Properties –

1. Is it possible to have a triangle with the following sides?

(i) 2 cm, 3 cm, 5 cm

Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

Here we can see,

(2 cm + 3 cm) = 5 cm

The sum of two sides of the triangle cannot be equal to the third side.

Therefore, a triangle with the sides 2 cm, 3 cm, 5 cm is not possible.

(ii) 3 cm, 6 cm, 7 cm

Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

Let us try all possible combinations:

3 cm + 6 cm = 9 cm > 7 cm

3 cm + 7 cm = 10 cm > 6 cm

6 cm + 7 cm = 13 cm > 3 cm

Therefore, we can see that the sum of any two sides is greater than the third side.

Therefore, a triangle with the sides 3 cm, 6 cm, 7 cm is possible.

(iii) 6 cm, 3 cm, 2 cm

Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

Here we can see,

(3 cm + 2 cm) = 5 cm < 6 cm

The sum of two sides of the triangle cannot be less than the third side. Therefore, a triangle with the sides 6 cm, 3 cm, 2 cm is not possible.

2. Take any point O in the interior of a triangle PQR.

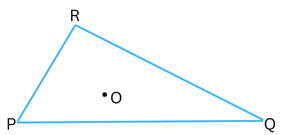
Is

(i) OP + OQ > PQ?

(ii) OQ + OR > QR?

(iii) OR + OP > RP?

Answer:

We join the point O with the three vertices P, Q, R of ΔPQR.

Three new triangles have been formed in the interior of the bigger triangle – namely ΔOPQ, ΔORP and ΔORQ.

(i) For triangle ΔOPQ:

OP + OQ > PQ (Since the sum of the lengths of any two sides of a triangle is greater than the third side)

(ii) For triangle ΔORQ:

OQ + OR > QR (Since the sum of the lengths of any two sides of a triangle is greater than the third side)

(iii) For triangle ΔORP: OR + OP > RP (Since the sum of the lengths of any two sides of a triangle is greater than the third side)

3. AM is a median of a triangle ABC.

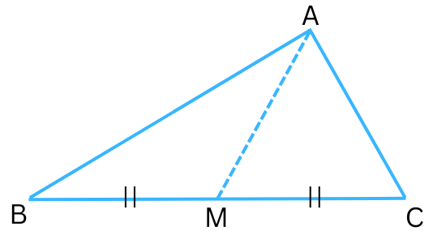
Is AB + BC + CA > 2 AM?

(Consider the sides of triangles ΔABM and ΔAMC.)

Answer:

Answer:

In ΔABM,

(AB + BM) > AM (Since the sum of the lengths of any two sides of a triangle is greater than the third side)

In ΔAMC,

(MC + CA) > AM (Since the sum of the lengths of any two sides of a triangle is greater than the third side)

Therefore, adding we get:

(AB + BM) + (MC + CA) > AM + AM

or, AB + (BM + MC) + CA > 2AM

or, AB + BC + CA > 2AM (Since, BC = BM + MC)

4. ABCD is a quadrilateral.

Is AB + BC + CD + DA > AC + BD?

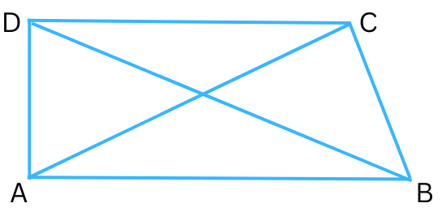
Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

In ΔABC,

(AB + BC) > AC ………..(i)

In ΔBCD,

(BC + CD) > BD .………(ii)

In ΔCDA,

(CD + DA) > AC .………(iii)

In ΔDAB,

(DA + AB) > BD .………(iv)

Now, we add (i), (ii), (iii) and (iv) together to get:

AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD

or, 2AB + 2BC + 2CD + 2DA > 2CA + 2DB

or, 2(AB + BC + CA + DA) > 2(CA + DB) or, AB + BC + CA + DA > CA + DB (Hence proved)

5. ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)

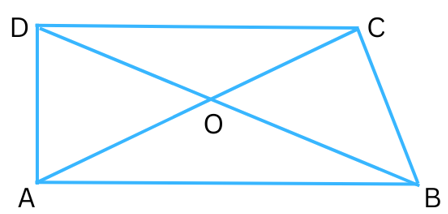
Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

In ΔOAB,

(OA + OB) > AB ………..(i)

In ΔOBC,

(OB + OC) > BC .………(ii)

In ΔOCD,

(OC + OD) > CD .………(iii)

In ΔODA,

(OD + OA) > DA .………(iv)

Now, we add (i), (ii), (iii) and (iv) together to get:

OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA

or, 2OA + 2OB + 2OC + 2OD > AB + BC + CD + DA

or, 2(OA + OB + OC + OD) > AB + BC + CD + DA

or, 2(OA + OC + OB + OD) > AB + BC + CD + DA

or, 2(AC + BD) > AB + BC + CD + DA (Since AC = OA + OC and BD = OB + OD) or, AB + BC + CD + DA < 2(AC + BD) (Hence proved)

6. The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?

Answer:

We know, the sum of the lengths of any two sides of a triangle is greater than the third side.

Therefore,

Length of third side < 12 cm + 15 cm

or, Length of third side < 27 cm

We also know, the difference between the lengths of any two sides of a triangle is smaller than the third side.

Therefore,

Length of third side > 15 cm – 12 cm

or, length of third side > 3 cm

Therefore, 27 cm > length of third side > 3 cm.

We conclude that the length of third side falls between 3 cm and 27 cm.

Solutions to Exercise 6.5 (Page No 105) of NCERT Class 7 Math Chapter 6 The Triangle and its Properties –

1. PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.

Answer: Please to the figure of the given triangle below:

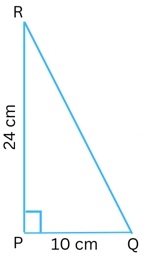
In the above triangle, ∠RPQ = 90⁰, the hypotenuse = RQ and the two legs PQ = 10 cm and PR = 24 cm.

Using the Pythagoras property, we know that in a right-angled triangle the square of the hypotenuse = sum of the squares of the legs.

Therefore,

RQ² = PQ² + PR²

or, RQ² = 10² + 24²

or, RQ² = 100 + 576

or, RQ² = 676

or, RQ = √676 or, RQ = 26 cm

2. ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.

Answer: Please to the figure of the given triangle below:

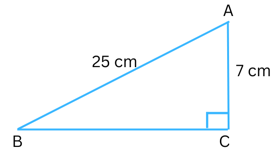
In the above triangle, ∠ACB = 90⁰, the hypotenuse = AB = 25 cm and the two legs are AC = 7 cm and BC.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore,

AB² = AC² + BC²

or, 25² = 7² + BC²

or, 625 = 49 + BC²

or, BC² = 576

or, BC = √576

or, BC = 24 cm

3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

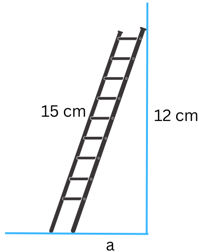
Answer:

You can see from the above figure that the ladder forms a right-angled triangle where the hypotenuse = 15 cm, and the two legs are of length a and 12 cm.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore,

15² = a² + 12²

or, 225 = a² + 144

or, a² = 225 – 144

or, a² = 81

or a = √81 

or a = 9 Therefore, the distance of the foot of the ladder from the wall = 9 cm.

4. Which of the following can be the sides of a right triangle?

(i) 2.5 cm, 6.5 cm, 6 cm.

(ii) 2 cm, 2 cm, 5 cm.

(iii) 1.5 cm, 2cm, 2.5 cm.

In the case of right-angled triangles, identify the right angles.

Answer:

(i) 2.5 cm, 6.5 cm, 6 cm.

The hypotenuse is the longest side in a right-angled triangle. So, let the hypotenuse be = 6.5 cm. Then the two legs are 2.5 cm and 6 cm.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore,

(6.5)² = (2.5)² + 6²

or, 42.25 = 6.25 + 36

or, 42.25 = 42.25

Since, LHS = RHS we can confirm that the triangle is indeed right-angled.

(ii) 2 cm, 2 cm, 5 cm.

The hypotenuse is the longest side in a right-angled triangle. So, let the hypotenuse be = 5 cm. Then the two legs are 2 cm and 2 cm.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore we get,

(5)² = (2)² + (2)²

or, 25 = 4 + 4

25 = 8, which is impossible.

Therefore, the give triangle is not right-angled.

Also can see:

2 cm + 2 cm < 5 cm (This is also not possible, because we know the sum of the lengths of any two sides of a triangle is greater than the third side).

So, we can in fact say that the triangle with the above three sides cannot exist.

(iii) 1.5 cm, 2cm, 2.5 cm

The hypotenuse is the longest side in a right-angled triangle. So, let the hypotenuse be = 2.5 cm. Then the two legs are 1.5 cm and 2 cm.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore,

(2.5)² = (1.5)² + 2²

or, 6.25 = 2.25 + 4

or, 6.25 = 6.25

Since, LHS = RHS we can confirm that the triangle is indeed right-angled.

5. A tree is broken at a height of 5 m from the ground, and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

Answer: Please refer to the figure below:

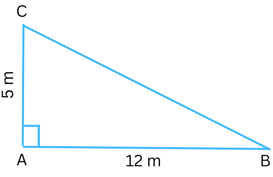
We can see that the tree broke at the point C. The part of the tree that is still standing is AC = 5 m.

The top touches the ground at the point B which is 12 m away from the base of the tree. Therefore, AB = 12 m.

ABC is a right-angled triangle.

Using the Pythagoras property, we know that in a right-angled the square of the hypotenuse = sum of the squares of the legs.

Therefore,

(BC)² = (AB)² + (AC)²

or, (BC)² = 12² + 5²

or, (BC)² = 144 + 25

or, (BC)² = 169

or, BC = √169

or, BC = 13 m Therefore, the original height of the tree = (AC + CB) = (5 m + 13 m) = 18 m.

6. Angles Q and R of a ΔPQR are 25⁰ and 65⁰.

Write which of the following is true:

(i) PQ² + QR² = RP²

(ii) PQ² + RP² = QR²

(iii) RP² + QR² = PQ²

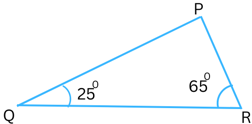
Answer:

In ΔPQR, ∠PQR = 25⁰ and ∠PRQ = 65⁰.

Now, the sum of the interior angles in a triangle always = 180⁰.

So,

∠PQR + ∠PRQ + ∠QPR = 180⁰

or, 25⁰ + 65⁰ + ∠QPR = 180⁰

or, 90⁰ + ∠QPR = 180⁰

or, ∠QPR = 180⁰ – 90⁰

or, ∠QPR = 90⁰

Therefore angle P is the right-angle, QR is the hypotenuse, PQ and RP are the legs.

Therefore using Pythagoras theorem,

PQ² + RP² = QR²

Hence, (ii) PQ² + RP² = QR² is true.

7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Answer: Please refer to the rectangle ABCD below:

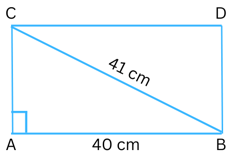
Length of the rectangle = AB = 40 cm

The diagonal BC = 41 cm.

ABC is a right-angled triangle with ∠CAB = 90⁰.

Therefore using Pythagoras theorem,

AB² + AC² = BC²

or, 40² + AC² = 41²

or, 1600 + AC² = 1681

or, 1600 + AC² = 1681

or, AC² = 1681 – 1600

or, AC² = 81

or, AC = √81

or, AC = 9 cm

So the breadth of the rectangle = AC = 9 cm.

Therefore, the perimeter of the rectangle ABCD = 2 (length + breadth) = 2(40 cm + 9 cm) = 2 × 49 cm = 98 cm.

8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

Answer: The figure of the rhombus is shown below:

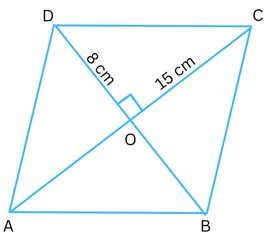
AC and BD are the diagonals of a rhombus. AC = 30 cm and BD = 16 cm.

The diagonals of a rhombus bisect each other at 90⁰. They intersect at point O as shown.

So, DO = OB = 16/2 cm = 8 cm

and, AO = OC = 30/2 cm = 15 cm

Now in triangle DOC,

DO = 8 cm, OC = 15 cm, ∠DOC = 90⁰.

Using Pythagoras theorem,

DC² = DO² + OC²

or, DC² = 8² + 15²

or, DC² = 64 + 225

or, DC² = 289

or DC = √289

or DC = 17 cm (This is the length of the side)

The length of all sides of a rhombus are equal, so each side = 17 cm.

So, the perimeter of the rhombus = 4 × 17 cm = 68 cm.

Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 6 The Triangle and its Properties:

Very Short Answer Type Questions:

1. How many angles in an isosceles triangle are equal?
Answer:
Two angles in an isosceles triangle are equal.

2. Where does the altitude of an obtuse-angled triangle lie?
Answer:
The altitude of an obtuse-angled triangle will lie outside the triangle.

3. Name a triangle for which the altitude and the median is the same?
Answer:
The altitude and the median is the same for an isosceles triangle.

4. Give one angle of a triangle with sides 4 cm, 4 cm, 4cm.
Answer:
The triangle is an equilateral triangle. Therefore, each angle = 60⁰.

5. How many exterior angles does a triangle have?
Answer:
A triangle has 6 exterior angles.

6. The following are the angles of a triangle: 60⁰, 60⁰ and 70⁰. What kind of a triangle is it?
Answer:
Sum of the angles of the triangle = 60⁰ + 60⁰ + 70⁰ = 190⁰ which is greater than 180⁰. This is impossible and the triangle cannot exist.

7. Three angles of a triangle are 60⁰, 70⁰ and 50⁰. What kind of a triangle is it?
Answer:
The angles are all acute. Therefore, the triangle is an acute-angled triangle.

8. Name a triangle in which the exterior angles formed at each vertex are equal.
Answer:
Equilateral triangle. Exterior angles formed at each vertex = 120⁰.

9. Give an impossible value for the exterior angle of a triangle.
Answer:
An impossible value for the exterior angle of a triangle = 180⁰.

10. Can you have a triangle with all the three angles less than 60⁰?
Answer:
No. The sum of the angles of the triangle always = 180⁰. Hence, the above scenario is impossible.

Multiple Choice Questions (MCQ):

1. If two angles of a triangle are 45⁰ each, what type of triangle is it?

(a) Right-angled
(b) Isosceles right-angled
(c) Isosceles
(d) Scalene

Answer: (b) Isosceles right-angled

Third angle of the triangle = 180⁰ – 45⁰ – 45⁰ = 90⁰ and two sides are equal.

Therefore, it is an isosceles right-angled triangle.

2. One angle of an isosceles triangle is 100⁰. What are the values of the other two angles?

(a) 40⁰ each
(b) 100⁰, 20⁰
(c) 50⁰, 30⁰
(d) Not enough information

Answer: (a) 40⁰ each

Sum of angles in a triangle = 180⁰.

Therefore, the given angle in the isosceles triangle = 100⁰ must be the unequal angle.

Let the other two equal angles be x each.

Therefore,

100⁰ + x + x = 180⁰

or, 100⁰ + 2x = 180⁰

or, 2x = 180⁰ – 100⁰

or, 2x = 80⁰

or, x = 80/2 or, x = 40⁰

3. Let the sides of a square be x. What is the length of the diagonal?

(a) √2x
(b) √3x
(c) 2x
(d) 2x²

Answer: (a) √2x

Using Pythagoras Theorem,

(Length of diagonal)² = x² + x²

or, (Length of diagonal)² = 2x² or, Length of diagonal = √2x

4. Two diagonals of a square are drawn to form four triangles. What kind of triangles are they?

(a) Right-angled
(b) Isosceles
(c) Equilateral
(d) Isosceles right-angled

Answer: (d) Isosceles right-angled

The two diagonals intersect each other at right angles and the diagonals are equal and bisect each other. Therefore, in each of the four triangles formed two sides are equal and one angle is a right angle. Therefore, the triangle is an isosceles right-angled triangle.

5. Two sides of a triangle are 6 cm and 8 cm. What are the possible values of the third side?

(a) 2 cm
(b) 3 cm
(c) 15 cm
(d) 1 cm

Answer: (b) 3 cm

Two sides of a triangle are 6 cm and 8 cm.

Therefore, third side > 8 cm – 6 cm

or, third side > 2 cm

Thus (a) 2 cm and (d) 1 cm can be eliminated.

Now, two sides of the triangle is always greater than the third side.

Therefore,

6 cm + 8 cm > third side.

So, the third side cannot be = 15 cm because that violates the above condition. Therefore, a possible value of the third side = 3 cm.

Short and Long Answer Type Questions:

1. The angles of a triangle are in the ratio of 1 : 2 : 3. What kind of a triangle is it?

Answer:

Let the angles be x, 2x and 3x.

Therefore,

x + 2x + 3x = 180⁰

or, 6x = 180⁰

or, x = 180/6

or, x = 30⁰

2x = 60⁰

3x = 90⁰ Therefore, the triangle is a right-angled triangle.

2. Three sides of a triangle are 6, 8 and 10. What kind of a triangle is it?

Answer:

We observe that,

6² + 8² = 10² Therefore, using Pythagoras Theorem we conclude that the triangle is right-angled.

3. Refer to the figure below. What is the area of rectangle BECD.

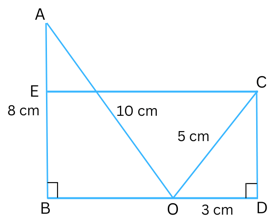
Answer:

In Δ ABO, AB = 8 cm, AO = 10 cm and ∠ ABO = 90⁰.

Using the Pythagoras Theorem,

AB² + BO² = AO²

or, 8² + BO² = 10²

or, 64 + BO² = 100

or, BO² = 100 – 64

or, BO² = 36

or, BO = √36

or, BO = 6 cm

In Δ CDO, CO = 5 cm, OD = 3 cm and ∠ CDO = 90⁰.

Using the Pythagoras Theorem,

CD² + OD² = CO²

or, CD² + 3² = 5²

or, CD² = 25 – 9

or, CD² = 16

or, CD = √16

or, CD = 4 cm

Now in rectangle BECD,

BD = BO + OD = 6 cm + 3 cm = 9 cm

CD = 4 cm Area of BECD = length × breadth = 9 × 4 = 36 cm²

4. The sides of a triangle 5 cm, 3 cm, 2 cm. Can we form a triangle with the three sides?

Answer:

Three sides of the triangle are 5 cm, 3 cm, 2 cm.

We have,

5 cm – 3 cm = 2 cm

However, for a triangle to exist difference between any two sides is always less than the third side.

Therefore, a triangle with sides 5 cm, 3 cm, 2 cm cannot exist.

5. The value of an exterior angle of a triangle is k. One of the interior opposite angles is k/2. What kind of a triangle is it?

Answer:

Exterior angle = Sum of interior opposite angles

Exterior angle = k and one of the interior opposite angles is k/2.

Value of the other interior opposite angle = k – k/2 = k/2 . Therefore, the interior opposite angles are equal and so the triangle is an isosceles triangle.

6. Find the angles x and y in the figure below. Use only formula related to triangles.

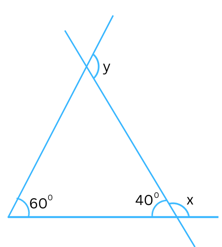
Answer:

We know,

Exterior angle in a triangle = sum of interior opposite angles

Therefore,

y = 60⁰ + 40⁰ = 100⁰

Now, sum of all angles of a triangle = 180⁰.

Third angle of the triangle = 180⁰ – 60⁰ – 40⁰ = 80⁰

Again using the formula that exterior angle in a triangle = sum of interior opposite angles we get: x = 60⁰ + 80⁰ = 140⁰

7. In the figure below ABCD is a square and E is the mid-point of CD. Find EA and EB. What kind of triangle is Δ ABE?

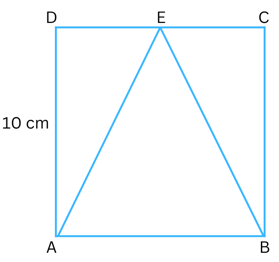
Answer:

Each side of square ABCD = 10 cm.

So, DC = 10 cm.

DE = EC = 10/2 = 5 cm.

∠ ADE = 90⁰.

Therefore, in Δ ADE using Pythagoras Theorem:

AE² = AD² + DE²

or, AE² = 10² + 5²

or, AE² = 125

or, AE = √125

or, AE = 5√5

Similarly, we can find that EB = 5√5.

In Δ ABE we get AE = EB = 5√5. Therefore, it is an isosceles triangle.

8. In the figure below find that angle ∠ BDE.

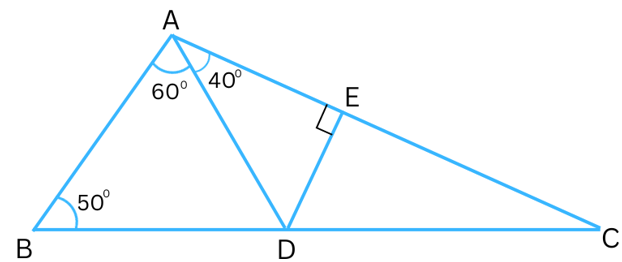
Answer:

In Δ ABD,

∠ ABD + ∠ADB + ∠BAD = 180⁰

or, 50⁰ + ∠ADB + 60⁰ = 180⁰

or, ∠ADB + 110⁰ = 180⁰

or, ∠ADB = 180⁰ – 110⁰

or, ∠ADB = 70⁰

Now in Δ AED,

∠ DAE + ∠AED + ∠ ADE = 180⁰

or, 40⁰ + 90⁰ + ∠ ADE = 180⁰

or, 130⁰ + ∠ ADE = 180⁰

or, ∠ ADE = 180⁰ – 130⁰

or, ∠ ADE = 50⁰

∠ BDE = ∠ADB + ∠ ADE = 70⁰ + 50⁰ = 120⁰

9. In the figure below Δ ABC and Δ DBC are isosceles triangles. Prove that ∠ ABD = ∠ACD.

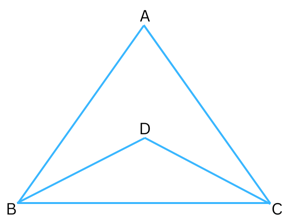
Answer:

In Δ ABC,

∠ ABC = ∠ ACB (Isosceles triangle)

In Δ DBC,

∠ DBC = ∠ DCB (Isosceles triangle)

Therefore,

∠ ABC – ∠ DBC = ∠ ACB – ∠ DCB

or, ∠ ABD = ∠ACD (Proved)

Fill in the Blanks:

(a) The three angles of a triangle can be rearranged into a ________ angle.

(b) If the altitudes of the triangle are two of its sides, the triangle is __________.

(c) The sum of the exterior angle of a triangle and its adjacent interior angle is _________.

(d) There are _________ medians and __________ altitudes in a triangle.

(e) In an isosceles triangle the median divides the triangle into two triangles which have equal _________.


Answers:


(a) The three angles of a triangle can be rearranged into a straight angle.

(b) If the altitudes of the triangle are two of its sides, the triangle is right-angled.

(c) The sum of the exterior angle of a triangle and its adjacent interior angle is 180⁰.

(d) There are three medians and three altitudes in a triangle.

(e) In an isosceles triangle the median divides the triangle into two triangles which have equal area.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 6 The Triangle and its Properties: