Solutions to NCERT Class 7 Math Chapter 7 Comparing Quantities:

Welcome students! Looking for solutions to Chapter 7? We have the latest version of the solutions right here. As usual, we’ve done our best to make them lucid and easy-to-understand. You should be able to grasp the concepts easily. Study the extra material we have included as well for more practice.

Solutions to Exercise 7.1 (Page No 115) of NCERT Class 7 Math Chapter 7 Comparing Quantities –

1. Convert the given fractional numbers to per cents.

(a) 1/8

Answer:

To convert to per cents we have,

1/8 = (1/8) × (100/100) = (1/8) × 100% = (100%)/8 = 12.5%

(b) 5/4

Answer:

To convert to per cents we have,

5/4 = (5 × 25)/(4 × 25) = 125/100 = 125%

(c) 3/40

Answer:

To convert to per cents we have,

3/40 = 3/40 × 100/100 = ((3 × 100)/40) × 1/100 = 7.5 × 1/100 = 7.5/100 = 7.5 %

(d) 2/7

Answer:

To convert to per cents we have,

2/7 = 2/7 × 100/100 = 2/7 × 100% = ((2 × 100)/7)% = 200/7% = 28 4/7 %

2. Convert the given decimal fraction to percent.

(a) 0.65

Answer:

To convert to percent we have,

0.65 = 0.65 × 100% = (65/100) × 100% = 65%

(b) 2.1

Answer:

To convert to percent we have,

2.1 = 2.1 × 100% = (21/10) × 100% = 210%

(c) 0.02

Answer:

To convert to percent we have,

0.02 = 0.02 × 100% = (2/100) × 100% = 2%

(d) 12.35

Answer:

To convert to percent we have, 12.35 = 12.35 × 100% = (1235/100) × 100% = 1235%

3. Estimate what part of the figures is coloured, and hence find the per cent which is coloured.

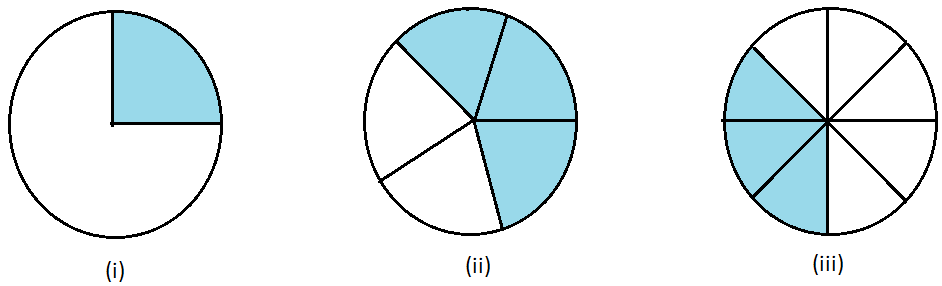
Answer:

(i) From the figure, we can say that 1/4 part of circle is shaded.

Therefore we convert the fraction to percentage:

1/4 = (1/4) × (100/100) = (1/4) × 100% = 25%

So, the percentage that is coloured = 25%.

(ii) The circle in (ii) is divided into 5 equal parts, out of which 3 parts are shaded.

Therefore, the fraction that is shaded = 3/5.

Therefore we convert the fraction to percentage:

3/5 = (3/5) × (100/100) = (3/5) × 100% = 60%

So, the percentage that is coloured = 60%.

(iii) The circle in (iv) is divided into 8 equal parts, out of which 3 parts are shaded.

Therefore, the fraction that is shaded = 3/8

Therefore we convert the fraction to percentage:

3/8 = (3/8) × (100/100) = (3/8) × 100% = 300/8 % = 37.5%

So, the percentage that is coloured = 37.5%.

4. Find:

(a) 15% of 250

Answer:

15% of 250 = (15/100) × 250 = 3750/100 = 37.5

(b) 1% of 1 hour

Answer:

1 hour = 60 mins

1% of 1 hour = 1% of 60 mins = (1/100) × 60 mins = 3/5 mins.

1 min = 60 secs

So, 3/5 mins = (3/5 × 60) mins = 36 secs.

Therefore, 1% of 1 hour = 36 secs.

(c) 20% of ₹ 2500

Answer:

20% of ₹ 2500 = 20/100 × ₹ 2500 = ₹ 500

(d) 75% of 1 kg

Answer:

1 kg = 1000 g 75% of 1 kg = 75% of 1000 g = 75/100 × 1000 g = 750 g.

5. Find the whole quantity if

(a) 5% of it is 600

Answer:

Let the whole quantity be x.

5% of x = 600

or, (5/100) × (x) = 600

or, x/20 = 600

or, x = 600 × 20

or, x = 12000

(b) 12% of it is ₹ 1080.

Answer:

Let the whole quantity be x.

12% of x = ₹ 1080

or, (12/100) × (x) = ₹ 1080

or, x = ₹ 1080 × 100/12

or, x = ₹ 9000

or, x = ₹ 9000

(c) 40% of it is 500 km

Answer:

Let the whole quantity be x.

40% of x = 500 km

or, (40/100) × (x) = 500 km

or, x = 500 km × 100/40

or, x = 1250 km

(d) 70% of it is 14 minutes

Answer:

Let the whole quantity be x.

70% of x = 14 mins

or, (70/100) × (x) = 14 mins

or, x = 14 mins × 100/70

or, x = 20 mins

(e) 8% of it is 40 litres

Answer:

Let the whole quantity be x.

8% of x = 40 litres

or, (8/100) × (x) = 40 litres

or, x = 40 litres × 100/8

or, x = 500 litres

6. Convert given per cents to decimal fractions and also to fractions in simplest forms:

(a) 25%

Answer:

25% = 25/100

Therefore, 25/100 = 0.25 (Expressed in decimal fractions)

And 25/100 = (25 ÷ 25)/(100 ÷ 25) = 1/4 (Reduced to the fraction in simplest form)

(b) 150%

Answer:

150% = 150/100

Therefore, 150/100 = 1.5 (Expressed in decimal fractions)

And 150/100 = (150 ÷ 50)/(100 ÷ 50) = 3/2 (Reduced to the fraction in simplest form)

(c) 20%

Answer:

20% = 20/100

Therefore, 20/100 = 0.2 (Expressed in decimal fractions)

And 20/100 = (20 ÷ 20)/(100 ÷ 20) = 1/5 (Reduced to the fraction in simplest form)

(d) 5%

Answer:

5% = 5/100

Therefore, 5/100 = 0.05 (Expressed in decimal fractions)

And 5/100 = (5 ÷ 5)/(100 ÷ 5) = 1/20 (Reduced to the fraction in simplest form)

7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?

Answer:

Percentage of females = 30%.

Percentage of males = 40%.

It is given that the remaining are children.

When we add all the percentages together we should get 100%.

Therefore,

30% + 40% + (Percentage of children) = 100%

or, 70% + (Percentage of children) = 100%

or, Percentage of children = 100% – 70% or, Percentage of children = 30%

8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?

Answer:

Percentage of people who voted = 60%.

When we add all the percentages together we should get 100%.

Therefore,

60% + (Percentage of people who did not vote) = 100%

or, Percentage of people who did not vote = 100% – 60%

or, Percentage of people who did not vote = 40%

Therefore, the number of people who actually did not vote

= 40% of 15000

= (40/100) × 15000 = 6000

9. Meeta saves ₹ 4000 from her salary. If this is 10% of her salary. What is her salary?

Answer:

Let Meeta’s salary be ₹ x.

It is given that her savings is 10% of her salary which is = ₹ 4000.

So,

10% of ₹ x = ₹ 4000

or, (10/100) × x = 4000

or, x = 4000 × 100/10 

or, x = ₹ 40000

Therefore, Meeta’s salary be ₹ 40000.

10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?

Answer:

The number of matches that the local cricket team played = 20.

It won 25% of them.

Therefore,

The number of matches they won

= 25% of 20

= (25/100) × 20

= 5

Therefore, the number of matches they won = 5.

Solutions to Exercise 7.2 (Page No 122) of NCERT Class 7 Math Chapter 7 Comparing Quantities –

1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.

(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.

Answer:

The cost price (CP) of gardening shears = ₹ 250.

The selling price (SP) of gardening shears = ₹ 325.

Here the SP > CP, the there is a profit.

Profit = SP – CP = ₹ 325 – ₹ 250 = ₹ 75.

Profit per cent = (Profit/CP) × 100

= (75/250) × 100

= (75 × 100)/250

= 30%

(b) A refrigerator bought for ₹ 12,000 and sold at ₹ 13,500.

Answer:

The cost price (CP) of gardening shears = ₹ 12000.

The selling price (SP) of gardening shears = ₹ 13500.

Here the SP > CP, the there is a profit.

Profit = SP – CP = ₹ 13500 – ₹ 12000 = ₹ 1500.

Profit per cent = (Profit/CP) × 100

= (1500/12000) × 100

= 150000/12000 

= 12.5 %

(c) A cupboard was bought for ₹ 2,500 and sold at ₹ 3,000.

Answer:

The cost price (CP) of gardening shears = ₹ 2500.

The selling price (SP) of gardening shears = ₹ 3000.

Here the SP > CP, the there is a profit.

Profit = SP – CP = ₹ 3000 – ₹ 2500 = ₹ 500.

Profit per cent = (Profit/CP) × 100

= (500/2500) × 100

= 50000/2500 

= 20 %

(d) A skirt was bought for ₹ 250 and sold at ₹ 150.

Answer:

The cost price (CP) of gardening shears = ₹ 250.

The selling price (SP) of gardening shears = ₹ 150.

Here the SP < CP, the there is a loss.

Loss = CP – SP = ₹ 250 – ₹ 150 = ₹ 100.

Loss per cent = (Loss/CP) × 100

= (100/250) × 100

= 10000/250 

= 40 %

2. Convert each part of the ratio to percentage:

(a) 3 : 1

Answer:

The total of all parts = 1 + 3 = 4.

So, the first part comprises of 3 out of 4 parts = 3/4

The second part comprises of 1 out of 4 parts = 1/4

Therefore,

The first part as a percentage of the whole = 3/4 × 100 = 75%.

Also, the second part as a percentage of the whole = 1/4 × 100 = 25%.

(b) 2 : 3 : 5

Answer:

The total of all parts = 2 + 3 + 5 = 10.

So, the first part comprises of 2 out of 10 parts = 2/10

The second part comprises of 3 out of 10 parts = 3/10

The third part comprises of 5 out of 10 parts = 5/10

Therefore,

The first part as a percentage of the whole = 2/10 × 100 = 20%.

Also, therefore, the second part as a percentage of the whole = 3/10 × 100 = 30%.

Also, therefore, the third part as a percentage of the whole = 5/10 × 100 = 50%.

(c) 1 : 4

Answer:

The total of all parts = 1 + 4 = 5.

So, the first part comprises of 1 out of 5 parts = 1/5

The second part comprises of 4 out of 5 parts = 4/5

Therefore,

The first part as a percentage of the whole = 1/5 × 100 = 20%.

Also, the second part as a percentage of the whole = 4/5 × 100 = 80%.

(d) 1 : 2 : 5

Answer:

The total of all parts = 1 + 2 + 5 = 8.

So, the first part comprises of 1 out of 8 parts = 1/8

The second part comprises of 2 out of 8 parts = 2/8

The third part comprises of 5 out of 10 parts = 5/8

Therefore,

The first part as a percentage of the whole = 1/8 × 100 = 12.5%.

Also, therefore, the second part as a percentage of the whole = 2/8 × 100 = 25%.

Also, therefore, the third part as a percentage of the whole = 5/8 × 100 = 62.5%.

3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.

Answer:

The decrease in the population of the city (or amount of change) = 25000 – 24500 = 500.

Percentage decrease = (amount of change)/(original amount or base) × 100

= (decrease in the population )/(original amount or base) × 100 = (500/25000) × 100 = 2 %

4. Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the Percentage of price increase?

Answer:

The increase in the population of the city (or amount of change) = 370000 – 350000 = 20000.

Percentage increase = (amount of change)/(original amount or base) × 100

= (increase in the population )/(original amount or base) × 100 = (20000/350000) × 100 = 2000000/350000 = 40/7 = 5 5/7

5. I buy a T.V. for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?

Answer:

The Cost Price (CP) = ₹ 10000.

The percentage of profit = 20%.

Therefore, profit = 20% of ₹ 10000 = ₹ (20/100) × 10000 = ₹ 2000.

Therefore, the Selling price = Cost Price + profit = ₹ 10000 + ₹ 2000 = ₹ 12000.

So, the amount of I got for the T.V. = ₹ 12000.

6. Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?

Answer:

The Selling Price (SP) of the washing machine = ₹ 13500.

Let the Cost Price (CP) of the washing machine = ₹ x.

The percentage of loss = 20%.

Therefore, the amount of loss = 20% of (₹ x) = ₹ 20x/100

Loss = CP – SP

or, CP = SP + Loss

or, x = 13500 + 20x/100

or, x – 20x/100 = 13500

or, (100x – 20x)/100 = 13500

or, 80x/100 = 13500

or, x = 13500 × 100/80

or, x = ₹ 16875

Therefore, the Cost Price (CP) of the washing machine = ₹ 16875.

7. (i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the percentage of carbon in chalk.

Answer:

The total of all parts = 10 + 3 + 12 = 25.

So, carbon comprises of 3 out of 25 parts = 3/25.

Therefore, the percentage of carbon in chalk = (3/25 × 100%) = 12%.

(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?

Answer:

It is given that the amount of carbon = 3 g.

From (ii), we found that percentage of carbon in chalk = 12%.

Let the total weight of the chalk stick = x g.

So, the percentage of carbon in the chalk stick = 12% of x g = (12/100) × (x) g.

Therefore we get,

(12/100) × (x) = 3

or, x = 3 × (100/12) 

or, x = 25

Therefore, the weight of the chalk stick = 25 g.

8. Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?

Answer:

Let the Cost Price (CP) of the washing machine = ₹ 275.

The percentage of loss = 15%.

Let the Selling Price (SP) of the book = ₹ x.

The amount of loss = 15% of ₹ 275 = ₹ (15/100) × 275 = ₹ 41.25.

Loss = CP – SP

or, SP = CP – Loss

or, x = ₹ 275 – ₹ 41.25

or, x = ₹ 233.75 Therefore, the Selling Price (SP) of the washing machine = ₹ 233.75

9. Find the amount to be paid at the end of 3 years in each case:

(a) Principal = ₹ 1,200 at 12% p.a.

Answer:

Let the interest be I, the principal be P, the rate of interest be R% p.a., the time be T.

We know,

I = (P × R × T)/100

or, I = (1200 × 12 × 3)/100

or, I = ₹ 432.

Therefore, the amount to be paid at the end of 3 years in each case = (Principal + Interest) = (₹ 1200 + ₹ 432) = ₹ 1632.

(b) Principal = ₹ 7,500 at 5% p.a.

Answer:

Let the interest be I, the principal be P, the rate of interest be R% p.a., the time be T.

We know,

I = (P × R × T)/100

or, I = (7500 × 5 × 3)/100

or, I = ₹ 1125.

Therefore, the amount to be paid at the end of 3 years in each case = (Principal + Interest) = (₹ 7500 + ₹ 1125) = ₹ 8625.

10. What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?

Answer:

Let the interest be I, the principal be P, the rate of interest be R% p.a, the time be T.

It is given:

P = ₹ 56000

I = ₹ 280

T = 2 years

We have to find the rate of interest R% p.a.

We know,

I = (P × R × T)/100

or, 280 = (56000 × R × 2)/100

or, R = (280 × 100)/(56000 × 2)

or, R = 0.25%

Therefore, the required rate of interest = 0.25%.

11. If Meena gives an interest of ₹ 45 for one year at 9% rate p.a. What is the sum she has borrowed?

Answer:

Let the interest be I, the principal be P, the rate of interest be R% p.a, the time be T.

It is given:

I = ₹ 45

T = 1 year

We have to find the rate of interest P.

We know,

I = (P × R × T)/100

or, 45 = (P × 9 × 1)/100

or, P = (45 × 100)/9

or, P = ₹ 500

Therefore, the principal (the sum she has borrowed) = ₹ 500.

Important Questions from Previous NCERT Textbook:

Exercise 8.1 Page No: 157 (Old Textbook):

1. Find the ratio of:

(a) ₹ 5 to 50 paise

Answer:

₹ 1 = 100 paise

or, ₹ 5 = 5 × 100 paise = 500 paise

Therefore,

₹ 5 : 50 paise = 500 paise : 50 paise = 500/50 = 10/1 = 10 : 1.

(b) 15 kg to 210 g

Answer:

1 kg = 1000 g

or, 15 kg = 15 × 1000 g = 15000 g

Therefore,

15 kg: 210 g = 15000 g : 210 g = 15000/210 = (15000 ÷ 30)/(210 ÷ 30 ) = 500/7 = 500 : 7.

(c) 9 m to 27 cm

Answer:

1 m = 100 cm

9 m = 9 × 100 cm = 900 cm

Therefore,

9 m : 27 cm = 900 cm : 27 cm = 900/27 = (900 ÷ 9)/(27 ÷ 9) = 100/3 = 100 : 3.

(d) 30 days to 36 hours

Answer:

1 day = 24 hours

30 days = 30 × 24 hours = 720 hours

Therefore,

30 days : 36 hours = 720 hours : 36 hours = 720/36 = (720 ÷ 36)/(36 ÷ 36) = 20/1 = 20 : 1.

2. In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?

Answer:

For 6 students number of computers = 3.

For 1 student number of computers = 3/6.

Therefore, for 24 students number of computers needed = 24 × 3/6 = (24 × 3)/6 = 72/6 = 12.

3. Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.

Area of Rajasthan = 3 lakh km² and area of UP = 2 lakh km².

(i) How many people are there per km² in both these States?

(ii) Which State is less populated?

Answer:

(i) It is given that:

Population of Rajasthan = 570 lakhs.

Area of Rajasthan = 3 lakh km².

Therefore, the number of people per km² in Rajasthan = (570 lakh)/(3 lakh km²) = 190 per km².

Population of UP = 1660 lakhs.

Area of UP = 2 lakh km².

Therefore, the number of people per km² in UP = (1660 lakh)/(2 lakh km²) = 830 per km².

(ii) Since 190 per km² < 830 per km², Rajasthan is less populated than UP.

Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 7 Comparing Quantities:

Very Short Answer Type Questions:

1. Are the ratios 1 : 2 and 2 : 1 equivalent?
Answer:
No, they are different ratios.

2. Which percentage is greater 40% or 60%?
Answer:
60 % is greater.

3. What percentage is 200 of 300?
Answer:
Required percentage = 200/300 × 100 = 66 2/3 %.

4. The cost price of an item is the same as its sale price. What is the net profit or loss?
Answer:
There is no net profit or loss.

5. What is the final amount on a principal of ₹ 1000 at an interest rate of 1% at the end of two years?
Answer:
Interest = (P × R × T)/100 = (1000 × 1 × 2)/100 = ₹ 20.
Final amount = ₹ 1000 + ₹ 20 = ₹ 1020.

6. 9% of a number is equal to 81. What is the number?
Answer:
Let the number be x.
Therefore, 9x/100 = 81
or, x = 81 × 100/9
or, x = 900 (Answer)

7. Can the cost price be greater than the sale price?
Answer:
Yes, if the cost price is greater than the sale price then a loss is incurred.

8. Ramu ate 1/4 part of an apple and Anisa ate 3/4 part of an apple. What percent of the apple did each Ramu and Anisha eat?
Answer:
Percent of the apple Ramu ate = 1/4 × 100% = 25% and percent that Anisa ate = 3/4 × 100% = 75%.

9. Ramu ate 150% of a cake. What is wrong with this statement?
Answer:
The maximum Ramu can eat is the whole cake or 100% of the cake. It is impossible for him to have eaten 100% of the cake.

10. A map is given a scale of 2 cm = 100 km. If two cities are actually 200 km apart, what is the distance between them on the map?
Answer:
100 km means 2 cm on the map.
1 km means 2/100 cm on the map.
200 km means (2/100 × 200) cm = 4 cm on the map.

Multiple Choice Questions (MCQ):

1. One number is 0.2 times the other. What is the ratio of the two numbers?

(a) 1 : 10
(b) 2 : 10
(c) 0.2 : 10
(d) 2 : 100

Answer: (b) 2 : 10

Let the two numbers be a and b.

By the given problem a = 0.2b.

or, a/b = 0.2/1 = (0.2 × 10)/(1 × 10) = 2/10

or, a : b = 2 : 10

2. If the cost price of an item decreases then:

(a) Sale price increases
(b) Sale price and profit increases
(c) Profit increases
(d) Sale price and profit remain unchanged

Answer: (c) Profit increases

3. The sale price of an item is ₹ 100 and the loss percent is 20%. What is the cost price?

(a) ₹ 125
(b) ₹ 120
(c) ₹ 80
(d) ₹ 130

Answer: (a) ₹ 125

Sale price = Cost price – Loss

or, Sale price = Cost price – Loss percent × Cost price

Therefore,

Cost price – 20/100 × Cost price = 100

or, Cost price (1 – 20/100) = 100

or, Cost price × 80/100 = 100

or, Cost price = 100 × 100/80

or, Cost price = ₹ 125

4. What is 1% of one hour?

(a) 36 seconds
(b) 1 minute
(c) 30 seconds
(d) 6 minutes

Answer: (a) 36 seconds

1 hour = 60 × 60 seconds = 3600 seconds

1 % of one hour = (1/100) × 3600 = 36 seconds

5. Which of the following percentages is equal to a fraction greater than

(a) 100 %
(b) 120 %
(c) 90 %
(d) 80 %

Answer: (b) 120 %

120 % = 120/100 = 6/5 which is greater than 1.

Short and Long Answer Type Questions:

1. Find the ratio of:

(i) 1 paise to 1 rupee                          (ii) 5 paise to 2 rupees

Answers:

(i) 1 paise to 1 rupee

1 rupee = 100 paise

So the required ratio, 1 paise : 1 rupee is 1:100.

(ii) 5 paise to 2 rupees

1 rupee = 100 paise

2 rupees = 200 paise

So, the required ratio, 5 paise : 2 rupees is 5 : 200 = 1 : 40.

2. Which ratio is greater: 4 : 5 or 11 : 13 ?

Answer:

We convert 4/5 and 11/13 into fractions with a common denominator.

For this we take the LCM of 5, 13.

4/5 = (4 × 13)/(5 × 13) = 52/65

11/13 = (11 × 5)/(13 × 5) = 55/65

We can see that: 55/65 > 52/65 and so we conclude that 11/13 > 4/5 or 11:13 is the greater ratio.

3. The speeds of two cars are in the ratio of 3 : 2. What is the ratio of the distances covered by the cars in the same time?

Answer:

Let the speeds of the two cars be 3x and 2x.

Let us calculate the distances covered for time t.

Therefore,

Distance covered by the first car = Speed × Time = 3x × t = 3xt.

Distance covered by the second car = Speed × Time = 2x × t = 2xt. Therefore, ratio of the distances covered by the cars in the same time t is 3xt : 2xt = 3 : 2.

4. A, B and C share a box of chocolates in the ratio 2:3:5. If there are 50 chocolates, how many more chocolates does C get than A?

Answer:

Total number of parts = 2 + 3 + 5 = 10.

Out of 10 parts A receives 2 parts.

Number of chocolates that A receives = (2/10) × 50 = 10.

Out of 10 parts B receives 3 parts.

Number of chocolates that B receives = (3/10) × 50 = 15.

Out of 10 parts C receives 5 parts.

Number of chocolates that C receives = (5/10) × 50 = 25.

Therefore, C receives (25 – 10) = 15 chocolates more than A.

5. A juice drink is made by mixing juice and water in the ratio 3:2. How much water should be added to 12 litres of juice to maintain the ratio?

Answer:

The ratio will be maintained only if the two ratios are equivalent.

Let the amount of water added be x.

Therefore,

3/2 = 12/x (equivalent ratios)

We have, 3/2 = (3 × 4)/(2 × 4) = 12/8

Therefore, by comparing 12/x = 12/8 we have x = 8 litres.

Therefore, volume of water that should be added to 12 litres of juice to maintain the ratio = 8 litres.

6. A certain sum of money is kept at a certain rate of interest per year for a certain period of time. If the principal is doubled and rate is halved for the same time period, what will the ratio of the interest earned now to the interest earned before?

Answer:

Initially let the principal be ₹ P, rate of interest be R % per year and the time period be T years.

Therefore,

Interest (I₁) = (P × R × T)/100 = PRT/100

After that the principal became ₹ 2P, rate of interest be R/2 % per year and the time period remained T years.

Interest (I₂) = (2P × R × T)/(2 × 100) = PRT/100

The interest remains the same as before.

Therefore, the ratio of the interest earned now to the interest earned before is: I₁ : I₂ = 1 : 1

7. You are given two numbers in the ratio 1 : 2. If the smaller number is increased by 20% and the greater number is decreased by 20%, what is the new ratio of the two numbers?

Answer:

Initially let the smaller number be x and the bigger number be 2x.

The greater number decreased by 20 % becomes (2x – (20/100)2x) = (2x – 0.4x) = 1.6x.

The new ratio of the two numbers is 1.2x/1.6x = 12/16 = (12 ÷ 4)/(16 ÷ 4) = 3/4 = 3 : 4.

8. The profit percent on an item was initially 10%. Then it was increased to 20%.  What is the ratio of the new sale price to the old sale price?

Answer:

Let the cost price be x.

The profit percent on an item was initially 10 %.

Sale price = Cost Price + Profit Percent × Cost Price

Therefore, sale price = (x + 110x/100) = 210x/100 .

Then it was increased to 20 %.

Therefore, new sale price = (x + 120x/100) = 220x/100 .

Therefore, ratio of the new sale price to the old sale price = 220x/100 : 210x/100 = 220x/100 × 100/210x = 22/21 = 22 : 21.

9. A certain sum of money is kept in a bank at 1% simple interest per annum for 2 years. The same sum of money is kept in the bank at 1.5% simple interest per annum for 1 year. In which case would the interest obtained be higher?

Answer:

Initially the principal be ₹ P, rate of interest be 1 % per year and the time period be 2 years.

Therefore,

Interest (I₁) = (P × R × T)/100 = (P × 1 × 2)/100 = 2P/100

The same sum of money is kept in the bank at 1.5% simple interest per annum for 1 year.

Interest (I₂) = (P × R × T)/100 = (P × 1.5 × 1)/100 = 1.5P/100

Since 2P/100 > 1.5P/100 , the interest will be higher when the sum of money is kept in the bank at 1% simple interest per annum for 2 years.

10. In a class of 50 boys and 50 girls, 40% boys like cricket. What percent of the girls like cricket if the overall percentage of students in the class who like cricket is 30%?

Answer:

Number of boys who like cricket = (40/100) × 50 = 20.

Number of girls who like cricket = x.

Overall percentage of students who like cricket is 30%.

Total number of students in the class = 50 + 50 = 100.

Total number of students who like cricket = 20 + x

Therefore,

(20 + x)/100 = 30/100

or, 20 + x = 30

or, x = 30 – 20

or, x = 10

Required number of girls = 10.

So, the required percentage of girls = (10/50) × 100 = 20%.

Fill in the Blanks:

(a) The ratios 3 : 4 and 6 : 8 are _________.

(b) If 5 sweets cost ₹ 2.50, then 8 sweets will cost ₹ _________.

(c) Profit or loss is calculated as a percentage of _________.

(d) Equivalent ratios are said to be in __________.

(e) If A : B = 1 : 2 and B : C = 2 : 6, than A : C = __________.

Answers:

(a) The ratios 3 : 4 and 6 : 8 are equivalent.

(b) If 5 sweets cost ₹ 2.50, then 8 sweets will cost ₹ 4.

(c) Profit or loss is calculated as a percentage of cost price.

(d) Equivalent ratios are said to be in proportion.

(e) If A : B = 1 : 2 and B : C = 2 : 6, than A : C = 1 : 6.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 7 Comparing Quantities: