Hello students and welcome to our solutions on Chapter 11! We have addressed whatever problems you might be having with this chapter right here in this solutions material. The extra problem set will give you more practise and resembles exam problems, so study them well. We are confident that you will like them and benefit from them.
Solutions to Exercise 9.1 (Page No 151) of NCERT Class 7 Math Chapter 9 Perimeter and Area –
1. Find the area of each of the following parallelograms.
(a)
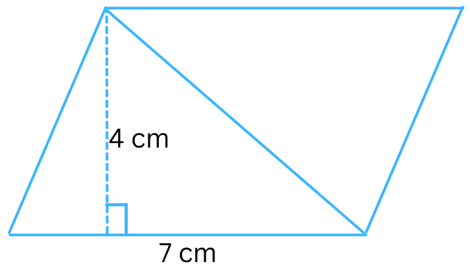
Answer:
Given: Length of base (b) = 7 cm, height (h) = 4 cm.
Area of the parallelogram = b × h = 7 cm × 4 cm = 28 cm2.
(b)
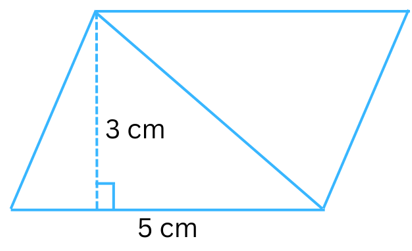
Answer:
Given: Length of base (b) = 5 cm, height (h) = 3 cm.
Area of the parallelogram = b × h = 5 cm × 3 cm = 15 cm2.
(c)
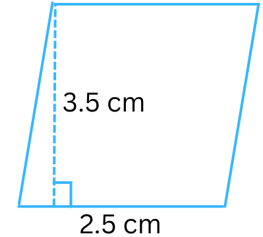
Answer:
Given: Length of base (b) = 2.5 cm, height (h) = 3.5 cm.
Area of the parallelogram = b × h = 2.5 cm × 3.5 cm = 8.75 cm2.
(d)
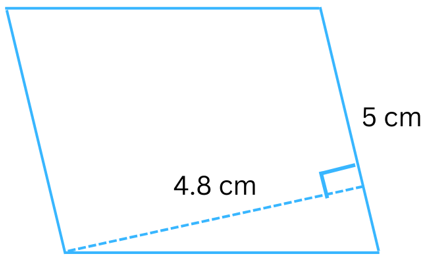
Answer:
Given: Length of base (b) = 5 cm, height (h) = 4.8 cm.
Area of the parallelogram = b × h = 5 cm × 4.8 cm = 24 cm2.
(e)
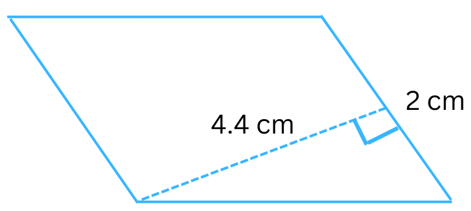
Answer:
Given: Length of base (b) = 2 cm, height (h) = 4.4 cm.
Area of the parallelogram = b × h = 2 cm × 4.4 cm = 8.8 cm2.
2. Find the area of each of the following triangles.
(a)
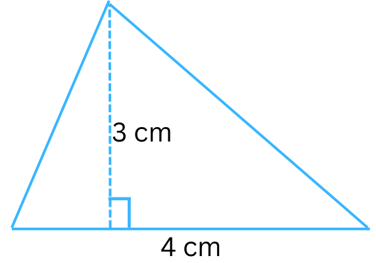
Answer:
Given: Length of base (b) = 4 cm, height (h) = 3 cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 4 cm × 3 cm = 6 cm2.
(b)
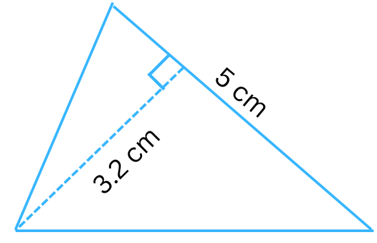
Answer:
Given: Length of base (b) = 5 cm, height (h) = 3.2 cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 5 cm × 3.2 cm = 8 cm2.
(c)
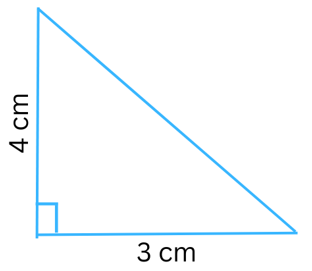
Given: Length of base (b) = 3 cm, height (h) = 4 cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 3 cm × 4 cm = 6 cm2.
(d)
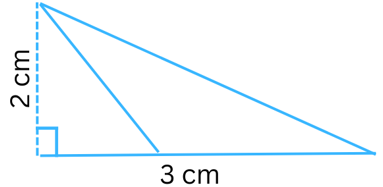
Answer:
Given: Length of base (b) = 3 cm, height (h) = 4 cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 3 cm × 2 cm = 3 cm2.
3. Find the missing values:
| S.No. | Base | Height | Area of the Parallelogram |
| a. | 20 cm | 246 cm2 | |
| b. | 15 cm | 154.5 cm2 | |
| c. | 8.4 cm | 48.72 cm2 | |
| d. | 15.6 cm | 16.38 cm2 |
Answer:
(a) Given: Length of base (b) = 20 cm
Area of the parallelogram = 246 cm2.
Let the height be = h cm.
Area of the parallelogram = base × height = b × h = 20 × h = 20h.
Therefore,
20h = 246
or, h = 246/20 = 12.3 cm
Therefore, the height of the parallelogram = 12.3 cm.
(b) Given: Area of the parallelogram = 154.5 cm2.
Let the height be = 15 cm.
Let the length of base = b cm.
Area of the parallelogram = base × height = b × h = b × 15 = 15b.
Therefore,
15b = 154.5
or, b = 154.5/15 = 10.3 cm
Therefore, the base of the parallelogram = 10.3 cm.
(c) Given: Area of the parallelogram = 48.72 cm2.
Let the height be = 8.4 cm.
Let the length of base = b cm.
Area of the parallelogram = base × height = b × h = b × 8.4 = 8.4b.
Therefore,
8.4b = 48.72
or, b = 48.72/8.4 = 5.8 cm
Therefore, the base of the parallelogram = 5.8 cm.
(d) Given: Length of base (b) = 15.6 cm
Area of the parallelogram = 16.38 cm2.
Let the height be = h cm.
Area of the parallelogram = base × height = b × h = 15.6 × h = 15.6h.
Therefore,
15.6h = 16.38
or, h = 16.38/15.6 = 1.05 cm
Therefore, the height of the parallelogram = 1.05 cm.
The completed table is shown below:
| S.No. | Base | Height | Area of the Parallelogram |
| a. | 20 cm | 12.3 cm | 246 cm2 |
| b. | 10.3 cm | 15 cm | 154.5 cm2 |
| c. | 5.8 cm | 8.4 cm | 48.72 cm2 |
| d. | 15.6 cm | 1.05 cm | 16.38 cm2 |
4. Find the missing values:
| Base | Height | Area of Triangle |
| 15 cm | ______ | 87 cm2 |
| ______ | 31.4 mm | 1256 mm2 |
| 22 cm | ______ | 170.5 cm2 |
Answers:
(a) Given: Length of base (b) = 15 cm.
Area of triangle = 87 cm2.
Let the height be = h cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 15 × h = 7.5h
Therefore,
7.5h = 87
or, h = 87/7.5 = 11.6 cm.
Therefore, the height of the triangle = 11.6 cm.
(b) Given: Height (h) = 31.4 mm
Area of triangle = 1256 mm2.
Let the length of the base be = b mm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × b × 31.4 = 15.7b
Therefore,
15.7b = 1256
or, b = 1256/15.7 = 80 mm.
Therefore, the base of the triangle = 80 mm.
(c) Given: Length of base (b) = 22 cm.
Area of triangle = 170.5 cm2.
Let the height be = h cm.
Area of the triangle = 1/2 × base × height = 1/2 × b × h = 1/2 × 22 × h = 11h
Therefore,
11h = 170.5
or, h = 170.5/11 = 15.5 cm.
Therefore, the height of the triangle = 15.5 cm.
The completed table is shown below:
| Base | Height | Area of Triangle |
| 15 cm | 11.6 cm | 87 cm2 |
| 80 mm | 31.4 mm | 1256 mm2 |
| 22 cm | 15.5 cm | 170.5 cm2 |
5. PQRS is a parallelogram (Fig). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) The area of the parallelogram PQRS (b) QN, if PS = 8 cm
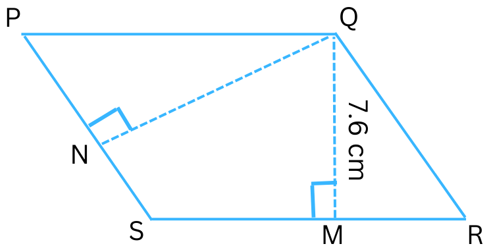
Answer:
(a)The area of the parallelogram PQRS = base × height = SR × QM = 12 × 7.6 = 91.2 cm2.
(b) It is given that PS = 8 cm
We found the area of the parallelogram in (a) as = 91.2 cm2.
Again,
Area = base × height
or, QN × PS = 91.2
or, QN × 8 = 91.2
or, QN = 91.2/8
or, QN = 11.4 cm
6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (Fig). If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.
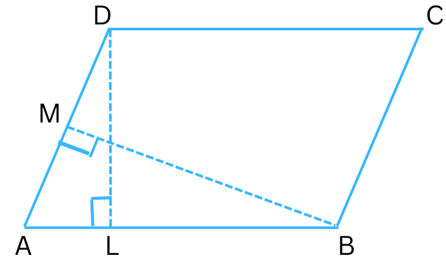
Answer:
It is given that the area of the parallelogram = 1470 cm2.
The area of the parallelogram ABCD = base × height = AB × DL = 35 × DL
Therefore,
35 × DL = 1470
or, DL = 1470/35
or, DL = 42 cm
Again, the area of the parallelogram ABCD = base × height = AD × BM = 49 × BM
Therefore,
49 × BM = 1470
or, BM = 1470/49
or, BM = 30 cm
7. ΔABC is right-angled at A (Fig). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm, and AC = 12 cm. Find the area of ΔABC. Also find the length of AD.

Answer:
Given: AB = 5 cm, AC = 12 cm
Area of ΔABC
= 1/2 × base × height
= 1/2 × AB × AC (Here we take AB as the base and AC as the height)
= 1/2 × 5 × 12
= 30 cm2
It is given that BC = 13 cm.
Again, area of ΔABC
= 1/2 × base × height
= 1/2 × BC × AD
= 1/2 × 13 × AD
We already found area of ΔABC = 30 cm2.
Therefore,
1/2 × 13 × AD = 30
or, AD = 30 × 2/13
or, AD = 4.6 cm
8. ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (Fig). The height AD from A to BC is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
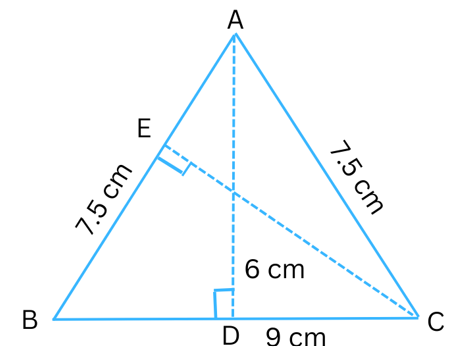
Answer:
It is given that BC = 9 cm and AD = 6 cm.
Area of ΔABC
= 1/2 × base × height
= 1/2 × BC × AD
= 1/2 × 9 × 6
= 27 cm2
It is given that AB = 7.5 cm.
Again, area of ΔABC
= 1/2 × base × height
= 1/2 × AB × CE
= 1/2 × 7.5 × CE
We already found the area of ΔABC = 27 cm2.
1/2 × 7.5 × CE = 27
or, CE = 27 × 2/7.5
or, CE = 7.2 cm
Solutions to Exercise 9.2 (Page No 158) of NCERT Class 7 Math Chapter 9 Perimeter and Area –
1. Find the circumference of the circles with the following radius: (Take π = 22/7)
(a) 14 cm
Answer:
Radius of the circle (r) = 14 cm.
Circumference of circle = 2πr = 2 × 22/7 × 14 cm = 88 cm.
(b) 28 mm
Answer:
Radius of the circle (r) = 28 mm.
Circumference of circle = 2πr = 2 × 22/7 × 28 mm = 176 mm.
(c) 21 cm
Answer:
Radius of the circle (r) = 21 cm.
Circumference of circle = 2πr = 2 × 22/7 × 21 cm = 132 cm.
2. Find the area of the following circles, given that:
(a) radius = 14 mm (Take π = 22/7)
Answer:
Radius of the circle (r) = 14 mm.
Area of the circle = πr2 = 22/7 × 142 = 616 mm2.
(b) diameter = 49 m
Answer:
Diameter = 49 m. Therefore, radius (r) = 49/2 = 24.5 m.
Area of the circle = πr2 = 22/7 × (24.5)2 = 1886.5 m2.
(c) radius = 5 cm
Answer:
Radius of the circle (r) = 5 cm.
Area of the circle = πr2 = 22/7 × 52 = 78.57 cm2.
3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π = 22/7)
Answer:
Let the radius of the circle = r m
Circumference of circle = 2πr, which is = 154 m (Given)
So,
2πr = 154
or, 2 × 22/7 × r = 154
or, r = 154 × 7/22 × 1/2
or, r = 24.5 m
So, the radius of the circle = 24.5 m.
Area of the sheet = πr2 = 22/7 × (24.5)2 = 1886.5 m2.
4. A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of the fence. Also find the cost of the rope, if it costs ₹ 4 per meter. (Take π = )
Answer:
The diameter of the circular garden = 21 m. Therefore, radius (r) = 21/2 = 10.5 m.
Therefore, circumference of the circular garden = 2πr = 2 × 22/7 × 10.5 m = 66 m.
If he makes 2 rounds of the fence, the length of the rope he needs to purchase will be equal to twice the circumference.
Therefore,
The length of the rope = 2 × 66 m = 132 m.
Cost of 1 m of the rope = ₹ 4.
Therefore, cost of 132 m of the rope = ₹ 4 × 132 m = ₹ 528.
5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Answer:
Area of the circular sheet of radius 4 cm = πr2 = π × 42 = 50.24 cm2.
Area of the circle of radius 3 cm which is removed = πr2 = π × 32 = 28.26
Therefore, area of the remaining sheet = (50.24 – 28.26) cm2 = 21.98 cm2.
6. Saima wants to put lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
Answer:
The diameter of the circular table cover = 1.5 m. Therefore, radius (r) = 1.5/2 = 0.75 m.
Therefore, circumference of the circular table cover = 2πr = 2 × 3.14 × 0.75 = 4.71 m.
The length of the lace required = the circumference of the circular table cover = 4.71 m.
The cost of one meter of the lace costs ₹ 15.
Therefore, the total cost = 4.71 × ₹ 15 = ₹ 70.65.
7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
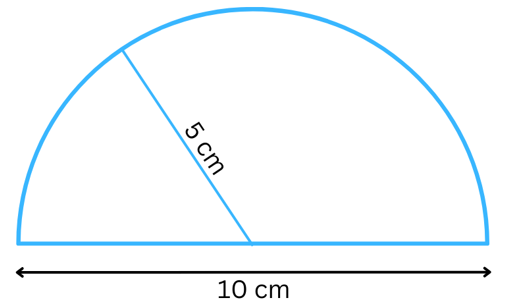
Answer:
The diameter of the semicircle = 10 cm. Therefore, radius (r) = 10/2 = 5 cm.
Circumference of the semicircle = half the circumference of the circle.
So, circumference of the semicircle = 2πr/2 = πr = 3.14 × 5 cm = 15.7 cm.
The perimeter of the figure = Circumference of the semicircle + Length of the Diameter
or, the perimeter of the figure = 15.7 cm + 10 cm = 25.7 cm.
8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
Answer:
The diameter of the circular table cover = 1.6 m. Therefore, radius (r) = = 0.8 m.
Area of the circular table-top = 2 = 3.14 × (0.8)2 = 2.0096 m2.
To polish 1 m2 the cost = ₹ 15.
Therefore, the cost of polishing 2.0096 m2 = 2.0096 × ₹ 15 = ₹ 30.144.
9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = 22/7)
Answer:
It is given that the wire of length 44 cm is formed into a circle.
Hence, the circumference of the circle = the length of the wire = 44 cm.
Let the radius of the circle be r cm.
So, the circumference of the circle = 2πr.
Therefore,
2πr = 44
or, 2 × 22/7 × r = 44
or, r = (44 × 7)/(2 × 22)
or, r = 7 cm
Area of the circle = πr2 = 22/7 × 72 = 154 cm2.
The same wire is bent into the shape of a square.
Then the perimeter of the square = the length of the wire = 44 cm
Perimeter of the square = 4 × (Length of each side)
Therefore,
4 × (Length of each side) = 44
or, Length of each side = 44/4
or, Length of each side = 11 cm.
Are of the square = (Length of each side)2 = (11 cm)2 = 121 cm2.
Since 154 cm2 > 121 cm2, the circle encloses more area.
10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. (Take π = 22/7)

Answer:
The radius of the circular card sheet = 14 cm.
So, the area of the circular card sheet = πr2 = 22/7 × 142 = 616 cm2.
The radii of both the smaller circles which are removed = 3.5 cm.
So, the area of each of the smaller circles = πr2 = 22/7 × (3.5)2 = 38.5 cm2.
Area of the rectangle of length 3 cm and breadth 1 cm.
Area of the rectangle = length × breadth = 3 cm × 1 cm = 3 cm2.
Hence, the total area that is removed = (38.5 cm2 + 38.5 cm2 + 3 cm2) = 80 cm2.
Therefore, the area of the remaining sheet = (616 cm2 – 80 cm2) = 536 cm2.
11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Answer:
Each side of the square piece of the aluminium sheet = 6 cm.
The area of the aluminium sheet = (6 cm)2 = 36 cm2.
The radius (r) of the circle that is cut out = 2 cm.
The area of the circle that is cut out = πr2 = 3.14 × 22 = 12.56 cm2.
Therefore, the area of the left over aluminium sheet = (36 cm2 – 12.56 cm2) = 23.44 cm2.
12. The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Answer:
Let the radius of the circle be r cm.
So, the circumference of the circle = 2πr.
Therefore,
2πr = 31.4
or, 2 × 3.14 × r = 31.4
or, r = 31.4/(3.14 × 2)
or, r = 5 cm.
So, the radius of the circle = 5 cm.
Area of the circle = πr2 = 3.14 × (5 cm)2 = 78.5 cm2.
13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
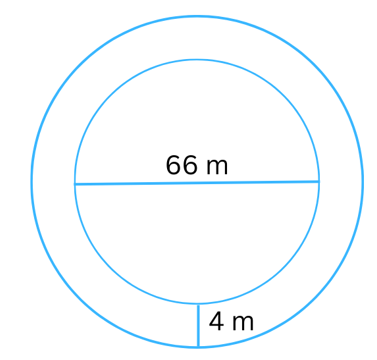
Answer:
The inner circle in the figure represents the flower bed.
The diameter of the flower bed = 66 m. Therefore, radius (r) = 66/2 = 33 m.
Area of the flower bed = πr2 = 3.14 × 332 = 3419.46 m2.
The width of the path surrounding the flower bed = 4 m.
Therefore, the radius of the outer circle = (33 + 4) m = 37 m.
Area of the outer circle (comprising of the flower bed + plus the path) = πr2 = 3.14 × 372 = 4298.66 m2.
Area of the path = Area of the outer circle – Area of the flower bed = (4298.66 – 3419.46) m2 = 879.2 m2.
14. A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Answer:
The area of the circular flower garden = 314 m2.
The radius (r) of sprinkler at the centre of the garden = 12 m.
Area of the flower bed = πr2 = 3.14 × 122 = 452.16 m2.
Since 452.16 m2 > 314 m2 we can say that the sprinkler can cover a lot more area beyond the area of the garden.
Therefore, we conclude that the sprinkler can water the entire garden.
15. Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
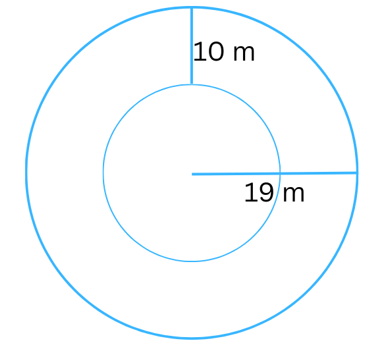
Answer:
From the figure we have: The radius (r) of the outer circle = 19 m.
Therefore, the circumference of the outer circle = 2πr = 2 × 3.14 × 19 = 119.32 m.
We find the radius of the inner circle = (19 m – 10 m) = 9 m.
Therefore, the circumference of the inner circle = 2πr = 2 × 3.14 × 9 = 56.52 m.
16. How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = 22/7)
Answer:
We know, that the distance around a circular region is known as its circumference.
When a wheel makes one complete rotation, it covers a distance equal to its circumference.
Therefore, to cover a distance of 352 m the wheel must rotate a certain number of times which is = Total distance/circumference.
Total distance = 352 m = 35200 cm (1 m = 100 cm)
The radius (r) of the wheel = 28 cm.
Circumference = 2πr = 2 × 22/7 × 28 = 176 cm.
Therefore, the number of times the wheel must rotate = 35200/176 = 200.
17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Answer:
In 1 hour the tip of the minute hand undergoes one complete rotation. Hence, it completes a distance equal to the circumference of the circle with radius (r) = the length of the minute hand of the clock.
The length of the minute hand of the clock = 15 cm.
This is actually the radius of the circle the minute hand moves through in 1 hour.
Therefore, taking radius (r) = 15 cm we get the circumference = 2πr = 2 × 3.14 × 15 = 94.2 cm.
Important Questions from Previous NCERT Textbook:
Exercise 11.1 Page No: 208 (Old Textbook):
1. The length and breadth of a rectangular piece of land are 500 m and 300 m respectively. Find
(i) its area (ii) the cost of the land, if 1 m2 of the land costs ₹ 10,000.
Answer: The figure of the rectangle is shown below:

(i) Length of the rectangular piece of land = 500 m.
Breadth of the rectangular piece of land = 300 m.
Area = Length × Breadth = 500 m × 300 m = 150000 m2.
(ii) The cost of 1 m2 of the land = ₹ 10,000.
Therefore, the cost of 150000 m2 = (150000 × ₹ 10000) = ₹ 1500000000.
2. Find the area of a square park whose perimeter is 320m.
Answer: The figure of the square park is shown below:

Let the length of each side of the square = a m.
Perimeter of the square = 4 × side = 4a m
It is given that perimeter = 320 m.
Therefore, 4a = 320
or, a = 320/4 = 80 m.
Area of the square = a2 = (80 m)2 = 6400 m2.
3. Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m. Also, find its perimeter.
Answer: The figure of the rectangular plot of land is shown below:
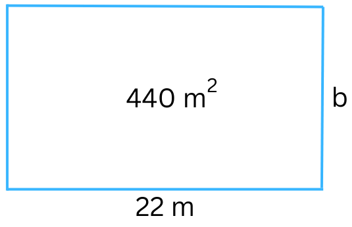
Length of the rectangle = 22 m.
Area of the rectangle = 440 m2.
Let the breadth of the rectangle = b m.
We know,
Area of the rectangle = Length × Breadth
or, 22 × b = 440
or, b = 440/22 = 20 m.
Perimeter = 2(length + breadth) = 2(22 m + 20 m) = 2 × 42 m = 84 m.
4. The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also, find the area.
Answer: The figure of the rectangular sheet is shown below:

Length of the rectangle = 35 cm.
Perimeter of a rectangular sheet = 100 cm.
Breadth of the rectangle = b cm.
Perimeter = 2(length + breadth)
or, 100 = 2(35 + b)
or, 35 + b = 100/2
or, b = 50 – 35
or, b = 15 cm
Therefore, the breadth of the rectangle = 15 cm.
Area = Length × Breadth
or area = 35 cm × 15 cm
or area of the rectangular sheet = 525 cm2
5. The area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
Answer: The figures of the square park and the rectangular park are both shown below:
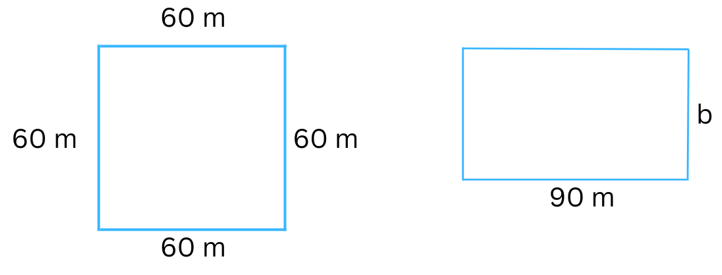
Side of the square = 60 m.
Area of the square = (Length of the side)2 = (60 m)2 = 3600 m2.
Length of the rectangular park = 90 m.
Let the breadth of the rectangular park = b m.
Area of the rectangle = Length × Breadth = 90 × b
We know,
Area of the rectangle = Area of the square
Therefore,
90 × b = 3600
or, b = 3600/90 = 40 m.
Therefore, the breadth of the rectangular park = 40 m.
6. A wire is in the shape of a rectangle. Its length is 40 cm, and its breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side? Also find which shape encloses more area?
Answer: The figures of the wire in rectangular form and square form (after being rebent) are both shown below:
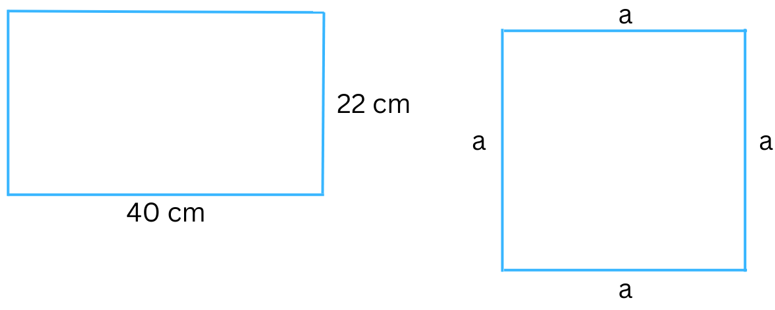
Length of the rectangle = 40 cm.
Breadth of the rectangle = 22 cm.
Perimeter = 2(length + breadth) = 2(40 cm + 22 cm) = 2 × 62 cm = 124 cm.
The same wire is formed into a square. So, the perimeter will remain the same.
Perimeter of the square = Perimeter of the rectangle
Perimeter of the square = 4 × side = 4a (Taking each side of the square to be a cm)
Therefore,
4a = 124
or, a = 124/4 = 31 cm.
So the measure of each side of the square = 31 cm.
Now,
Area of the rectangle = Length × Breadth = 40 cm × 22 cm = 880 cm2.
Are of the square = (Length of the side)2 = a2 = (31 cm)2 = 961 cm2.
Therefore, we conclude that the square encloses more area.
7. The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.
Answer: The figure of the rectangle is shown below:

Breadth of the rectangle = 30 cm.
Let the length of the rectangle = l cm.
The perimeter of a rectangle = 130 cm.
Perimeter of the rectangle = 2(length + breadth) = 130 cm.
or, 2(l + 30) = 130
or, l + 30 = 65
or, l = 65 – 30
or, l = 35 cm
So, the length of the rectangle = 35 cm.
Therefore, the area of the rectangle = Length × Breadth = 35 cm × 30 cm = 1050 cm2.
8. A door of length 2 m and breadth 1 m is fitted in a wall. The length of the wall is 4.5 m, and the breadth is 3.6 m (Fig). Find the cost of white washing the wall, if the rate of white washing the wall is ₹ 20 per m2.
Answer: The figure is shown below:
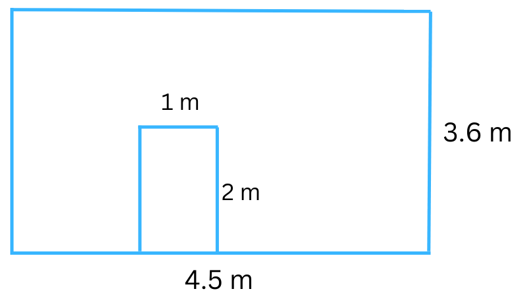
To find the cost of white washing the wall, we have to find the net area to be white washed.
Length of the rectangular wall = 4.5 m.
Breadth of the rectangular wall = 3.6 m.
Area of the rectangular wall = Length × Breadth = 4.5 m × 3.6 m = 16.2 m2.
Length of the door = 4.5 m.
Breadth of the door = 3.6 m.
Area of the rectangular door = Length × Breadth = 2 m × 1 m = 2 m2.
Therefore, the net area to be white washed = Area of the rectangular wall – Area of the rectangular door = 16.2 m2 – 2 m2 = 14.2 m2.
The rate of white washing the wall = ₹ 20 per m2.
Therefore, the total cost of white washing the wall = 14.2 m2 × ₹ 20 per m2 = ₹ 284.
Exercise 11.4 Page No 226 (Old Textbook):
1. A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside and around it. Find the area of the path. Also find the area of the garden in hectare.
Answer: The figure is shown below:

Let ABCD represent the rectangular garden and the shaded region represent the path 5 m wide.
To find the area of the path, we need to find (Area of rectangle PQRS – Area of rectangle ABCD)
It is given that AB = 90 m and BC = 75 m.
Therefore,
PQ = (90 + 5 + 5) m = 100 m.
QR = (75 + 5 + 5) m = 85 m.
Area of the rectangle ABCD = length × breadth = AB × BC = 90 × 75 m2 = 6750 m2.
Area of the rectangle PQRS = length × breadth = PQ × QR = 100 × 85 m2 = 8500 m2.
Area of the path = Area of the rectangle PQRS – Area of the rectangle ABCD = (8500 – 6750) m2 = 1750 m2.
We know,
1 hectare = 10000 m2
or, 1 m2 = 0.0001 hectare
Therefore, the area of the garden in hectare = (6750 × 0.0001) hectare = 0.675 hectare.
2. A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.
Answer: The figure is shown below:

Let ABCD represent the rectangular park and the shaded region represent the path 3 m wide.
To find the area of the path, we need to find (Area of rectangle PQRS – Area of rectangle ABCD)
It is given that AB = 125 m and BC = 65 m.
PQ = (125 + 3 + 3) m = 131 m.
QR = (65 + 3 + 3) m = 71 m.
Area of the rectangle ABCD = length × breadth = AB × BC = 125 × 65 m2 = 8125 m2.
Area of the rectangle PQRS = length × breadth = PQ × QR = 131 × 71 m2 = 9301 m2.
Area of the path = Area of the rectangle PQRS – Area of the rectangle ABCD = (9301 – 8125) m2 = 1176 m2.
3. A picture is painted on a cardboard 8 cm long and 5 cm wide, such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Answer: The figure is shown below:
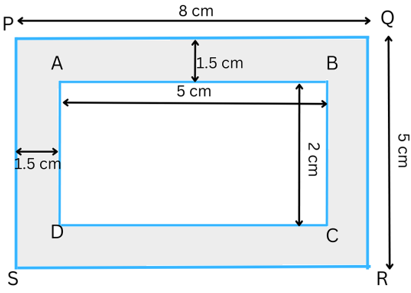
Let PQRS represent the entire cardboard, ABCD represent the painted picture and the shaded region represent the margin 1.5 cm wide.
To find the area of the path, we need to find (Area of rectangle PQRS – Area of rectangle ABCD)
It is given that PQ = 8 m and QR = 5 m.
Therefore,
AB = (8 – 1.5 – 1.5) m = 5 m.
BC = (5 – 1.5 – 1.5) m = 2 m.
Area of the rectangle PQRS = length × breadth = PQ × QR = 8 × 5 m2 = 40 m2.
Area of the rectangle ABCD = length × breadth = AB × BC = 5 × 2 m2 = 10 m2.
Area of the margin = Area of the rectangle PQRS – Area of the rectangle ABCD = (40 – 10) m2 = 30 m2.
4. A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find:
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate of ₹ 200 per m2.
Answer: The figure is shown below:
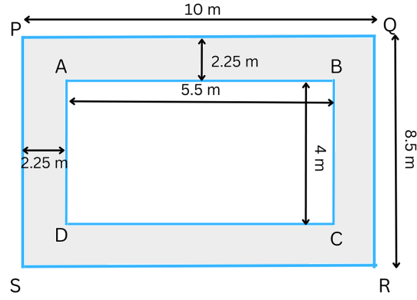
To find the area of the verandah, we need to find (Area of rectangle PQRS – Area of rectangle ABCD)
It is given that AB = 5.5 m and BC = 4 m.
Therefore,
PQ = (5.5 + 2.25 + 2.25) m = 10 m.
QR = (4 + 2.25 + 2.25) m = 8.5 m.
Area of the rectangle ABCD = length × breadth = AB × BC = 5.5 × 4 m2 = 22 m2.
Area of the rectangle PQRS = length × breadth = PQ × QR = 10 × 8.5 m2 = 85 m2.
Area of the verandah = Area of the rectangle PQRS – Area of the rectangle ABCD = (85 – 22) m2 = 63 m2.
(ii) For every 1 m2 the cost of cementing the floor = ₹ 200.
Therefore, the cost of cementing the entire verandah = (63 × ₹ 200) = ₹ 12600.
5. A path 1 m wide is built along the border and inside a square garden of side 30 m. Find:
(i) the area of the path.
(ii) the cost of planting grass in the remaining portion of the garden at the rate of ₹ 40 per m2.
Answer: The figure is shown below:
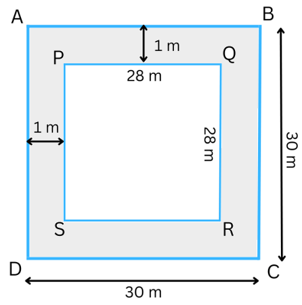
(i) Let ABCD represent the square garden and the shaded region represent the 1 m wide path.
To find the area of the path, we need to find (Area of rectangle – Area of rectangle ABCD)
It is given that each side of ABCD = 30 m.
Therefore,
PQ = (30 – 1 – 1) m = 28 m.
QR = (30 – 1 – 1) m = 28 m.
Area of the square ABCD = (length of each side)2 = 302 m2 = 900 m2.
Area of the square PQRS = (length of each side)2 = 282 m2 = 784 m2.
Area of the path = Area of the square ABCD – Area of the square PQRS = (900 – 784) m2 = 116 m2.
(ii) We already found the area of the remaining portion of the garden = Area of the square PQRS = 784 m2.
For every 1 m2 the cost of planting grass in the remaining portion of the garden = ₹ 40.
Therefore, the total cost of planting grass in the entire remaining portion of the garden = 784 × ₹ 40 = ₹ 31360.
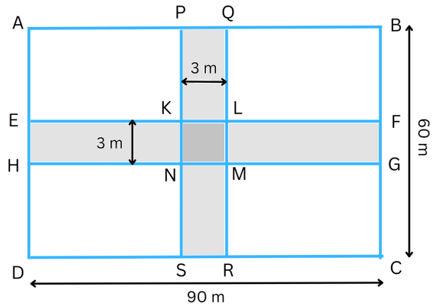
6. Two cross roads, each of width 10 m, cut at right angles through the centre of a rectangular park of length 700 m and breadth 300 m and parallel to its sides. Find the area of the roads. Also, find the area of the park excluding the crossroads. Give the answer in hectares.
Answer: The figure is shown below:

Area of the cross roads is the area of the shaded portion, i.e., the area of the rectangle PQRS and the area of the rectangle EFGH. But while doing this, note that the area of the square KLMN (darker shade of grey in the figure) is counted twice. Therefore, we have to subtract the area of the square KLMN once.
Now,
PQ = 10 m
PS = BC = 300 m
Therefore, area of rectangle PQRS = length × breadth = PQ × PS = 10 × 300 m2 = 3000 m2.
Now,
EH = 10 m
EF = CD = 700 m
Therefore, area of rectangle EFGH = length × breadth = EH × EF = 10 × 700 m2 = 7000 m2.
We observe, length of each side of the square KLMN = 10 m.
Area of the square KLMN = (length of side)2 = (10 m)2 = 100 m2.
Therefore, the area of the roads = area of rectangle PQRS + area of rectangle EFGH – area of the square KLMN = (3000 + 7000 – 100) m2 = 9900 m2.
1 hectare = 10000 m2
or, 1 m2 = 0.0001 hectare
Therefore, the area of the roads in hectares = (9900 × 0.0001) hectare = 0.99 hectares.
The total area of the park = (700 × 100) m2 = 210000 m2.
The area of the park excluding crossroads = The total area of the park – the area of the roads (210000 – 9900) m2 = 200100 m2.
In hectare, the area of the park excluding crossroads = (200100 × 0.0001) hectare = 20.01 hectare.
7. Through a rectangular field of length 90 m and breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
(i) the area covered by the roads.
(ii) the cost of constructing the roads at the rate of ₹ 110 per m2.
Answer: The figure is shown below:
(i) Area of the cross roads is the area of the shaded portion, i.e., the area of the rectangle PQRS and the area of the rectangle EFGH. But while doing this, note that the area of the square KLMN (darker shade of grey in the figure) is counted twice. Therefore, we have to subtract the area of the square KLMN once.
Now,
PQ = 3 m
PS = BC = 60 m
Therefore, area of rectangle PQRS = length × breadth = PQ × PS = 3 × 60 m2 = 180 m2.
Now,
EH = 3 m
EF = CD = 90 m
Therefore, area of rectangle EFGH = length × breadth = EH × EF = 3 × 90 m2 = 270 m2.
We observe, length of each side of the square KLMN = 3 m.
Area of the square KLMN = (length of side)2 = (3 m)2 = 9 m2.
Therefore, the area of the roads = area of rectangle PQRS + area of rectangle EFGH – area of the square KLMN = (180 + 270 – 9) m2 = 441 m2.
(ii) For every 1 m2 the cost of constructing the roads = ₹ 110.
Therefore, the total cost of constructing the roads = (441 × ₹ 110) = ₹ 48510.
8. Pragya wrapped a cord around a circular pipe of radius 4 cm (adjoining figure) and cut off the length required of the cord. Then she wrapped it around a square box of side 4 cm (also shown). Did she have any cord left? (π = 3.14)
Answer: The length required of the cord = circumference of the circular pipe.
The radius (r) = 4 cm.
Circumference of the circular pipe = 2πr = 2 × 3.14 × 4 = 25.12 cm.
Therefore, the length required of the cord = 25.12 cm.
The cord of length 25.12 cm is wrapped around a square box of side 4 cm.
The perimeter of the square box = 4 × (Length of side) = 4 × 4 = 16 cm.
So, the length of cord she has left after she has wrapped it around the square box = (25.12 – 16) cm = 9.12 cm.
9. The adjoining figure represents a rectangular lawn with a circular flower bed in the middle.
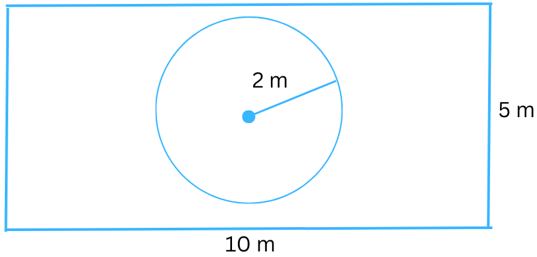
Find:
(i) the area of the whole land (ii) the area of the flower bed.
(iii) the area of the lawn, excluding the area of the flower bed.
(iv) the circumference of the flower bed.
Answer:
(i) The length of the rectangular lawn = 10 m.
The breadth of the rectangular lawn = 5 m.
Area of the rectangular lawn = length × breadth = 10 × 5 = 50 m2.
(ii) The radius (r) of the circular flower bed = 2 m.
Area of flower bed = πr2 = 3.14 × 22 = 12.56 m2.
(iii) The area of the lawn, excluding the area of the flower bed = (Area of the rectangular lawn – Area of flower bed) = (50 – 12.56) m2 = 37.44 m2.
(iv) The circumference of the flower bed = 2πr = 2 × 3.14 × 2 = 12.56 cm.
10. In the following figures, find the area of the shaded portions:
Answer:
(i) The first figure is shown below:
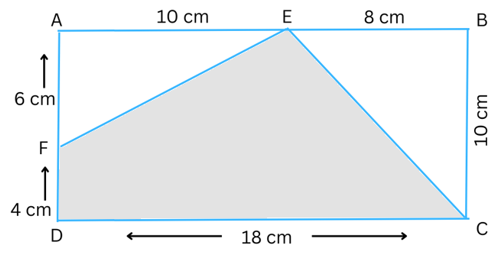
Area of the rectangle ABCD = Length × Breadth = (18 cm × 10 cm) = 180 cm2.
Area of ΔAEF = 1/2 × base × height = 1/2 × AE × AF = (1/2 × 10 × 6) cm2 = 30 cm2.
Area of ΔEBC = 1/2 × base × height = 1/2 × BC × EB = (1/2 × 10 × 8) cm2 = 40 cm2.
Therefore, the area of the shaded region FECD = Area of rectangle ABCD – Area of ΔAEF – Area of ΔEBC = (180 – 30 – 40) cm2 = 110 cm2.
(ii) The second figure is shown below:

Area of the square PQRS = (Length of side)2 = (20 cm)2 = 400 cm2.
Area of ΔQRU = 1/2 × base × height = 1/2 × UR × QR = (1/2 × 10 × 20) cm2 = 100 cm2.
Area of ΔTSU = 1/2 × base × height = 1/2 × SU × TS = (1/2 × 10 × 10) cm2 = 50 cm2.
Area of ΔQPT = 1/2 × base × height = 1/2 × PT × QP = (1/2 × 10 × 20) cm2 = 100 cm2.
Therefore, the area of the shaded region ΔQTU = (Area of the square PQRS – Area of ΔQRU – Area of ΔTSU – Area of ΔQPT) = (400 – 100 – 50 – 100) cm2 = 150 cm2.
11. Find the area of the quadrilateral ABCD.
Here, AC = 22 cm, BM = 3 cm,
DN = 3 cm, and
BM ⊥ AC, DN ⊥ AC
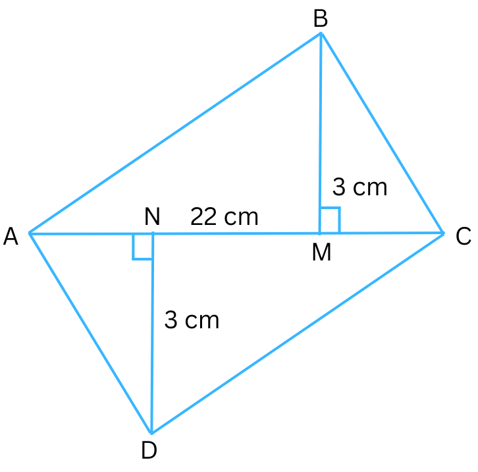
Answer:
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔADC
Area of ΔABC = 1/2 × base × height = 1/2 × AC × BM = (1/2 × 22 × 3) cm2 = 33 cm2.
Area of ΔACD = 1/2 × base × height = 1/2 × AC × DN = (1/2 × 22 × 3) cm2 = 33 cm2.
Therefore, area of quadrilateral ABCD = (33 + 33) cm2 = 66 cm2.
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 9 Perimeter and Area:
Very Short Answer Type Questions:
1. The length of a rectangle is twice its width. If the area is 288 cm2, find the length and width.
Answer:
Let length of a rectangle be 2x and width be x.
Area = Length × Breadth = 2x × x = 288
or, 2x2 = 288
or, x2 = 144
or, x = √144
or, x = 12 cm and 2x = 24 cm
Length = 24 cm and Width = 12 cm.
2. The sides of a square and an equilateral triangle are equal. If the perimeter of the square is 64 cm, find the perimeter of the triangle.
Answer:
Let each side of the square = each side of the equilateral triangle = a.
Therefore, 4a = 64 cm or, a = 16 cm.
Perimeter of the triangle = 3a = 16 × 3 = 48 cm.
3. A square has the same perimeter as a triangle with sides 2cm, 5 cm and 8 cm. What is the length of each side of the square?
Answer:
Perimeter of the square = perimeter of the triangle = 2 cm + 5 cm + 8 cm = 15 cm.
Length of each side of the square = 15/4 = 3.75 cm.
4. Out of a rectangular sheet of paper of area 16 cm2 two square pieces of area 2 cm2 are cut out. What is the area of the remaining sheet of paper?
Answer:
Area of the remaining sheet of paper = 16 cm2 – 2 cm2 – 2 cm2 = 12 cm2.
5. The base and altitude of a triangle are equal. The area of a triangle is 18 cm2. What is the length of the base?
Answer:
Base = altitude = b.
Therefore,
1/2 × b × b = 18
or, b2 = 18 × 2
or, b2 = 36
or, b = √36
or, b = 6 cm
Therefore, length of the base = 6 cm.
6. A square has area 40 cm2. If you draw the two diagonals, then what is the area of each of the four triangles thus formed?
Answer:
The area of the four triangles thus formed are equal. Area of each triangle = 1/4 × 40 cm2 = 10 cm2.
7. Two parallelograms of different shapes are given to you. The length of the base and also height of the parallelograms are equal. What can you say about the areas?
Answer:
Area of parallelogram = Length × Breadth. So, the areas of the parallelograms will be equal.
8. A circle has a radius of 7 cm. What is the area of one quarter of the circle?
Answer:
Area of the circle = πr2 = 22/7 × 72 = 154 cm2.
Therefore, area of one quarter of the circle= 154/4 = 38.5 cm2.
9. Give an example of a shape for which area increases as perimeter increases.
Answer:
Circle.
10. Express 40 m2 in cm2.
Answer:
1 m= 100 cm.
or, 1 m2 = 1 m × 1 m
or, 1 m2 = 100 cm × 100 cm
or, 1 m2 = 10000 cm2
or, 40 m2 = 40 × 10000 cm2
or, 40 m2 = 400000 cm2
Multiple Choice Questions (MCQs):
1. The area of a square is 64 cm2 and the area of another square is 16 cm2. What are the ratios of the perimeters?
(a) 2 : 1
(b) 4 : 1
(c) 3 : 1
(d) 16 : 1
Answer: (a) 2 : 1
For the first square, length of side = √64 = 8 cm.
For the second square, length of side = √16 = 4 cm.
So, perimeter of first square = 4 × 8 cm = 32 cm.
And perimeter of second square = 4 × 4 cm = 16 cm.
Ratio of perimeter of first square to perimeter of second square = 32 : 16 = 2 : 1.
2. The base of a triangle is half the length of a rectangle, and the height of the triangle is three-fourths the breadth of the rectangle. If the area of the triangle is 12 cm2, find the area of the rectangle.
(a) 64 cm2
(b) 16 cm2
(c) 32 cm2
(d) Need more information
Answer: (a) 64 cm2
Length of rectangle = l and breadth of rectangle = b.
Base of triangle = l/2 and height of triangle = 3b/4.
Area of triangle = 1/2 × base × height = 1/2 × l/2 × 3b/4 = 3lb/16
Therefore,
3lb/16 = 12
Area of rectangle = Length × Breadth = lb.
or, lb = (12 × 16)/3
or, lb = 64 cm2
3. Find the ratio of the perimeter to the area of the circle of given radius?
(a) 1 : r
(b) 3 : r
(c) 2 : r
(d) r : 2
Answer: (c) 2 : r
Perimeter of a circle = 2πr
Area of a circle = πr2
Perimeter/Area = 2πr/(πr2 ) = 2/r
or, Perimeter : Area = 2 : r
4. An equilateral triangle with length of one side = 6 cm has the same perimeter as an isosceles triangle with equal sides 4 cm. What is the length of the third side of the isosceles triangle?
(a) 12 cm
(b) 8 cm
(c) 10 cm
(d) 9 cm
Answer: (c) 10 cm
Perimeter of equilateral triangle = 6 cm × 3 = 18 cm.
Let the unequal side of the isosceles triangle be x.
Therefore, x + 4 + 4 = 18
or, x + 8 = 18
or, x = 18 – 8
or, x = 10 cm
5. If the radius of a circle is halved, by what percentage does the area change?
(a) 70%
(b) 80%
(c) 75%
(d) 50%
Answer: (c) 75%
If radius is r area = πr2
If the radius is halved new radius = r/2 .
New area = π(r/2)2 = (πr2)/4
New area decreased by = (πr2 – (πr2)/4) = (3πr2)/4 .
Percentage by which area decreases = ((3πr2)/4 ÷ πr2) × 100 = 75%.
Long and Short Answer Type Questions:
1. Two squares of area 16 cm2 are placed side by side such that they join each other. What is the perimeter of the rectangle thus formed?
Answer:
Length of side of both squares = √16 = 4 cm.
The two squares are placed side by side joining each other.
Length of the rectangle = 4 cm + 4 cm = 8 cm.
Breadth of the rectangle = 4 cm.
Therefore, perimeter = 2(length + breadth) = 2(8 + 4) = 24 cm.
2. A circle has a circumference of 22 cm. To increase its circumference to 44 cm, how much should the radius be increased?
Answer:
Initially the circumference = 22 cm.
2πr = 22
or, 2 × 22/7 × r = 22
or, r = (22 × 7)/(22 × 2)
or, r = 3.5 cm
After increasing the circumference to 44 cm.
2 × 22/7 × r = 44
or, r = (44 × 7)/(22 × 2)
or, r = 7 cm.
Therefore, the radius must be increased by (7 – 3.5) cm = 3.5 cm
3. A circular path of radius 6 cm has a 1 cm path all around it. What is the circumference of the outer path?
Answer:
Radius of outer path = 6 cm + 1 cm = 7 cm.
Circumference of the outer path= 2πr = 2 × 22/7 × 7 = 44 cm.
4. A circle is inscribed inside a square (touches all four sides). If the side of the square is a, what is the area of the circle?
Answer:
Refer to the figure below:
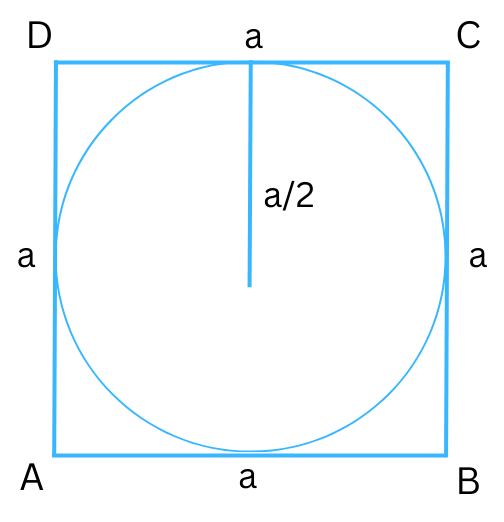
The side of the square is a.
Radius of the circle = a/2 .
Therefore, area of the circle = π(a/2)2 = (πa2)/4 .
5. You are given a right-angled triangle with sides 6 cm, 8 cm and 10 cm. What is the length of the altitude to the hypotenuse?
Answer:
By Pythagoras Theorem,
AB2 + BC2 = AC2
or, 82 + 62 = 102
Therefore, the hypotenuse must be 10 cm and the other two sides are 8 cm and 6 cm as shown below:

Now area of Δ ABC = 1/2 × AB × BC = 1/2 × 8 × 6 = 24 cm2.
The area of the triangle can also be computed as 1/2 × BD × AC = 1/2 × BD × 10.
Since the area remains the same,
1/2 × BD × 10 = 24 cm2
or, BD = (24 × 2)/10
or, BD = 4.8 cm
The length of the altitude to the hypotenuse = 4.8 cm.
6. The rectangle ABCD has length 8 cm and breadth 4 cm. A triangle is drawn in rectangle ABCD with BC as a common side and third vertex lying on AD. What is the area of part of the rectangle excluding the triangle?
Answer:
Please refer to the figure below:

Base of the triangle = Length of the rectangle = BC = 8 cm.
Altitude of the triangle = Breadth of the rectangle = EO = 4 cm.
Area of the triangle = 1/2 × Base × Height = 1/2 × BC × EO = 1/2 × 8 × 4 = 16 cm2.
Area of the rectangle = Length × Breadth = BC × CD = 8 × 4 = 32 cm2.
The area of part of the rectangle excluding the triangle = (32 – 16) cm2 = 16 cm2.
7. Two circles have a common centre. The radius of the smaller circle is 7 cm and the radius of the larger circle is 14 cm. What is the area of the region between the two circles?
Answer:
Area of the smaller circle = πr2 = 22/7 × 7 × 7 = 154 cm2.
Area of the larger circle = πr2 = 22/7 × 14 × 14 = 616 cm2.
Area between the region between the two circles with common centre = (616 – 154) cm2 = 462 cm2.
8. A circular pool is constructed in the rectangular garden as shown below. Find the area of the part of the garden excluding the pool.
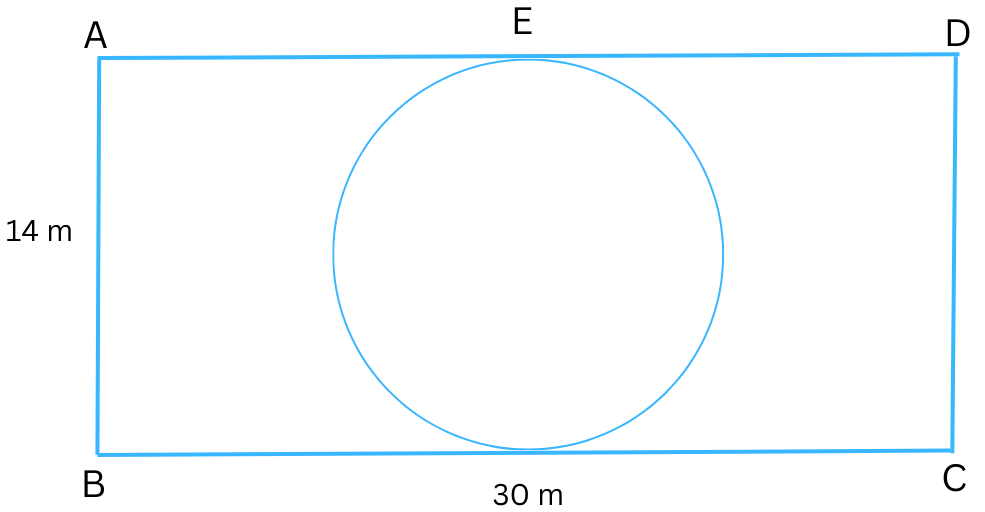
Answer:
From the figure we can that the diameter of the circle = 14 m.
Radius = 14/2 = 7 m.
Area of the circular pool = πr2 = 22/7 × 7 × 7 = 154 m2.
Area of the rectangular garden = Length × Breadth = 30 m × 14 m = 420 m2.
Area of the part of the garden excluding the pool = (420 – 154) = 266 m2.
9. A circular wheel of radius 14 cm completes one rotation in 3 seconds. How long does it take to cover 17.6 m?
Answer:
Distance covered in one rotation is equal to circumference = 2πr = 2 × 22/7 × 14 = 88 cm.
So the wheel covers 88 cm in 3 seconds.
The wheel covers 1 cm in 3/88 seconds.
17.6 m = 17.6 × 100 cm = 1760 cm.
The wheel covers 1760 cm in (3/88 × 1760) = 60 seconds = 60/60 = 1 minute.
10. You are given a rectangular sheet of paper. How can you decrease the area and increase the perimeter?
Answer:
You can cut off a small square piece from rectangle as shown below:
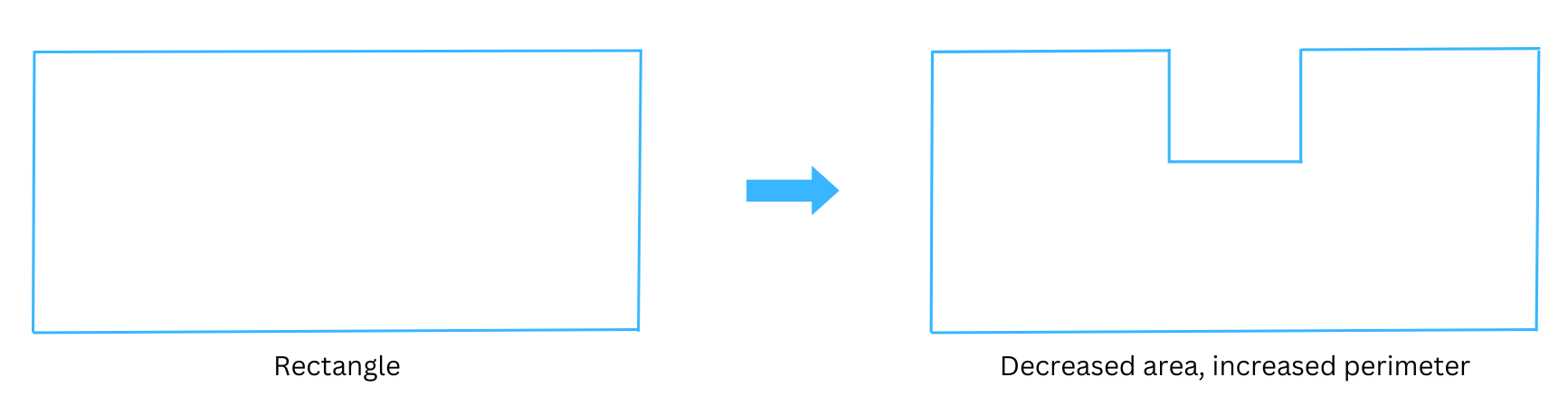
This adds extra boundaries to the rectangle and the perimeter increases. Since the square piece is cut off the area of the rectangle decreases.
Fill in the Blanks:
(a) 1 hectare = _________ m2.
(b) When the length and breadth of a rectangle become equal, it forms a _________.
(c) The area of two squares of side 2 cm is the same as the area of a rectangle of length 2 cm and breadth _________.
(d) The ratio of circumference to diameter of a circle is always ________.
(e) The diagonal of a parallelogram divides it into two triangles of equal _________.
Answers:
(a) 1 hectare = 10,000 m2.
(b) When the length and breadth of a rectangle become equal, it forms a square.
(c) The area of two squares of side 2 cm is the same as the area of a rectangle of length 2 cm and breadth 4 cm.
(d) The ratio of circumference to diameter of a circle is always π.
(e) The diagonal of a parallelogram divides it into two triangles of equal area.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 9 Perimeter and Area:
An expert team of Indian and foreign educated engineers and scientists have specifically prepared these exercise solutions and extra problem-set to show beginners the problem-solving techniques related to basic mensuration. If you follow the solutions step-by-step, you will be able to fully understand and implement the methods to solve unknown problems. We’ve done our best to make the concepts easy for you and are confident you will benefit from them.
The free versions of the solutions are available for you to download anytime! We aim to keep providing you with excellent study material and resources. So keep visiting our website and join our email list to use them to bolster your preparation!
The main topics covered are:
9.1 – Area of a Parallelogram
9.2 – Area of a Triangle
9.3 – Circles
Here are the number of problems by each chapter:
Exercise 9.1 – 8 questions
Exercise 9.2 – 17 questions
It is vital that you understand how the formulae and techniques are derived. You will find it much easier to solve problems (specially the tricky type), if you understand the underlying concepts. There will be problems, both objective-type and long-type in your exams which will test your understanding of the fundamentals. So first understand, and then apply.
There are many different kinds of problems that can be set from this chapter. The same concepts can be asked in many different ways. So, for this chapter we suggest that you find problems of many different types and closely study and practise the techniques used to solve them. Past papers and good reference books are an excellent starting point. You will increase in confidence and skill if you use this approach and fare well in your exams.
If you need additional help with your preparation – our expert teacher-mentors will be there for you anytime you need them! Feel free to get in touch with your requirements and let us help you out!
Reach out to us anytime you need additional tutoring and guidance. Whether it be top-quality coaching, exam preparation or even career mentoring – our expert teacher-mentors will be there for you every step of your journey. We provide on-demand one-to-one coaching, based on your convenience and your needs – have it completely your way! Just contact us with your requirements and let us get you on track! Book an appointment now!


