Solutions to NCERT Class 8 Mathematics Chapter 3 Understanding Quadrilaterals:

Welcome students! We have introduced you to many interesting geometry problem-solving methods in the Chapter 3 solutions. We have pretty much shown you all that you need to know to solve unknown problems. The solutions are designed scientifically to help you quickly grasp the topics. We only advise that you work out the problems by yourself by drawing the figures, alongside looking at your solutions. This approach will give you excellent practice.

Solutions to Exercise 3.1 (Page No 22) of NCERT Class 8 Mathematics Chapter 3 Understanding Quadrilaterals:

1. Given here are some figures.

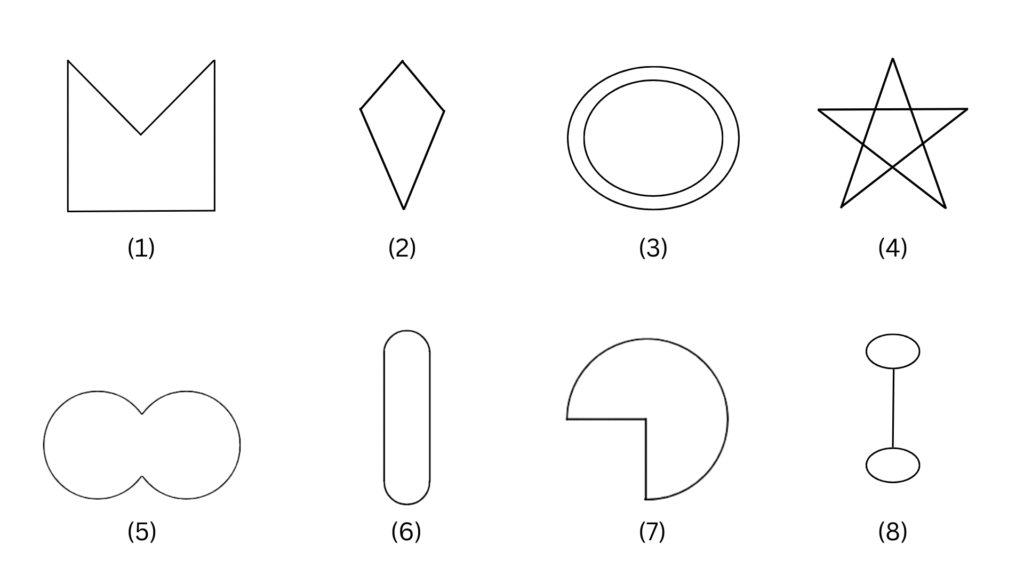
Classify each of them on the basis of the following.

(a) Simple curve                   (b) Simple closed curve                  (c) Polygon

(d) Convex polygon             (e) Concave polygon

Answer:

(a) Simple curve: 1, 2, 5, 6 and 7

(b) Simple closed curve: 1, 2, 5, 6 and 7

(c) Polygon: 1 and 2

(d) Convex polygon: 2

(e) Concave polygon: 1

2. What is a regular polygon?

State the name of a regular polygon of

(i) 3 sides                    (ii) 4 sides                  (iii) 6 sides

Answer: A regular polygon has sides of equal length and angles of equal measure. A regular polygon is both ‘equilateral’ and ‘equiangular’.

(i) 3 sides

An equilateral triangle is a regular polygon with three equal sides and three equal angles.

(ii) 4 sides

A square is a regular polygon with four equal sides and four equal angles.

(iii) 6 sides

A regular hexagon has six equal sides and six equal angles.

Summary: A regular polygon has sides of equal length and angles of equal measure. A regular polygon of (i) 3 sides is an equilateral triangle, a regular polygon of (i) 4 sides is a square and a regular polygon of (i) 6 sides is a regular hexagon.

Solutions to Exercise 3.2 (Page No 24) of NCERT Class 8 Mathematics Chapter 3 Understanding Quadrilaterals:

1. Find x in the following figures.

(a)

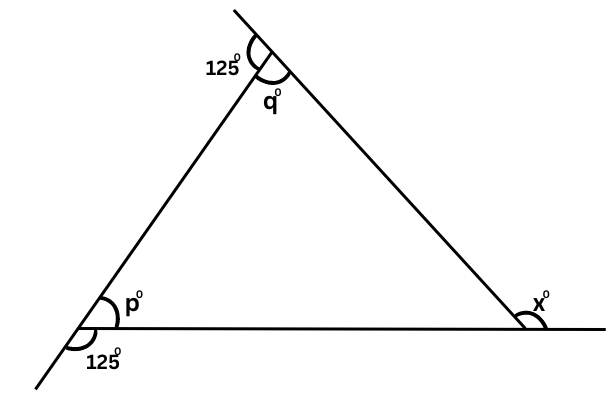
Answer:

125⁰ and p⁰ are supplementary.

Therefore, 125⁰ + p = 180⁰

or, p = 180⁰ – 125⁰ = 55⁰

125⁰ and q⁰ are supplementary.

Therefore, 125⁰ + q = 180⁰

or, q = 180⁰ – 125⁰ = 55⁰

x is the exterior angle of the triangle and p and q are the two interior opposite angles.

Therefore, x = p + q = 55⁰ + 55⁰ = 110⁰.

Another method:

Sum of exterior angles of a polygon = 360⁰.

x + 125⁰ + 125⁰ = 360⁰

or, x + 250⁰ = 360⁰

or, x = 360⁰ – 250⁰ = 110⁰.

(b)

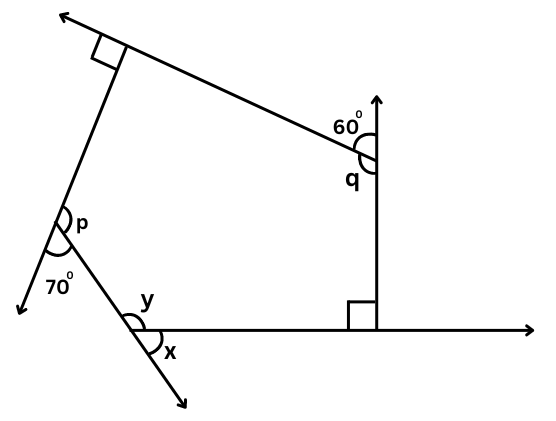
70⁰ and p⁰ are supplementary.

Therefore, 70⁰ + p = 180⁰

or, p = 180⁰ – 70⁰ = 110⁰

60⁰ and q⁰ are supplementary.

Therefore, 60⁰ + q = 180⁰

or, q = 180⁰ – 60⁰ = 120⁰

x⁰ and y⁰ are supplementary.

The sum of the angles of the polygon = (5 – 2) × 180⁰ = 540⁰.

Therefore,

110⁰ + 120⁰ + 90⁰ + 90⁰ + y = 540⁰

or, 410⁰ + y = 540⁰

or, y = 540⁰ – 410⁰ = 130⁰

x⁰ and y⁰ are supplementary.

x + y = 180⁰

or, x + 130⁰ = 180⁰

or, x = 180⁰ – 130⁰ = 50⁰

Another method:

Sum of exterior angles of a polygon = 360⁰.

90⁰ + 60⁰ + 90⁰ + 70⁰ + x = 360⁰

or, 310⁰ + x = 360⁰

or, x = 360⁰ – 310⁰ = 50⁰

Summary: In figure (a) x = 110⁰ and in figure (b) x = 50⁰.

2. Find the measure of each exterior angle of a regular polygon of

(i) 9 sides                (ii) 15 sides

Answers:

(i) 9 sides

Sum of the angles of a regular polygon with n sides = (n – 2) × 180⁰.

Therefore, the sum of the interior angles of a regular polygon with 9 sides = (9 – 2) × 180⁰ = 7 × 180⁰ = 1260⁰.

Measure of each interior angle = 1260/9 = 140⁰.

Exterior and interior angles are supplementary.

Therefore,

Each exterior angle = 180⁰ – 140⁰ = 40⁰

(ii) 15 sides

Sum of the angles of a regular polygon with n sides = (n – 2) × 180⁰.

Therefore, the sum of the interior angles of a regular polygon with 15 sides = (15 – 2) × 180⁰ = 13 × 180⁰ = 2340⁰.

Measure of each interior angle = 2340/15 = 156⁰.

Exterior and interior angles are supplementary.

Therefore,

Each exterior angle =180⁰ – 156⁰ = 24⁰

Summary: The measure of each exterior angle of a regular polygon of (i) 9 sides is 40⁰ and that of a regular polygon of (ii) 15 sides is 24⁰.

3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?

Answer:

Exterior and interior angles are supplementary.

Each exterior angle = 24⁰.

Sum of all exterior angles = 360⁰.

Number of sides = number of exterior angles = 360/24 = 15

Summary: If the measure of each exterior angle of a regular polygon is 24⁰, then the number of sides = 15.

5. (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?

    (b) Can it be an interior angle of a regular polygon? Why?

Answers:

(a) Exterior and interior angles are supplementary.

Each exterior angle = 22⁰.

Sum of all exterior angles = 360⁰.

Number of sides = number of exterior angles = 360/22 = 16.36.

The number of sides has to be an integer, hence such a regular polygon cannot exist.

(b) Each interior angle = 22⁰.

Sum of all interior angles = 360⁰.

Number of sides = number of interior angles = 360/22 = 16.36.

The number of sides has to be an integer, hence such a regular polygon cannot exist.

Summary: It is not possible to have a regular polygon with measure of each exterior angle or each interior angle as 22°. This is because the number of sides in these cases is a decimal value, which is not possible.

6. (a) What is the minimum interior angle possible for a regular polygon? Why?

(b) What is the maximum exterior angle possible for a regular polygon?

Answers:

(a)The regular polygon with the minimum number of sides will have the minimum possible interior angle. This is an equilateral triangle.

Therefore, the minimum interior angle = 180/3 = 60⁰.

As the number of sides increases in a regular polygon, the value of the interior angles also increases.

(b) We know that interior angles and exterior angles are supplementary because they form a linear pair.

Exterior angle = 180⁰ – interior angle.

Therefore, exterior angle is maximum when interior angle is minimum.

Since we found in (a) that an equilateral triangle has the minimum interior angle, it will also have the maximum exterior angle.

Therefore, maximum exterior angle = 180⁰ – 60⁰ = 120⁰.

Summary: (a) The minimum interior angle possible for a regular polygon is 60⁰ and (b) the maximum exterior angle possible for a regular polygon is 120⁰. Both are for an equilateral triangle.

Solutions to Exercise 3.3 (Page No 30) of NCERT Class 8 Mathematics Chapter 3 Understanding Quadrilaterals:

1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.

(i) AD = _________               (ii) ∠DCB = _________

(iii) OC = _________                          (iv) m ∠DAB + m ∠CDA = _________

Answers:

(i) AD = BC (Opposite sides of a parallelogram are equal)

(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal)

(iii) OC = OA (Diagonals of a parallelogram bisect each other)

(iv) m ∠DAB + m ∠CDA = 180⁰ (The adjacent angles in a parallelogram are supplementary)

2. Consider the following parallelograms. Find the values of the unknown x, y, z.

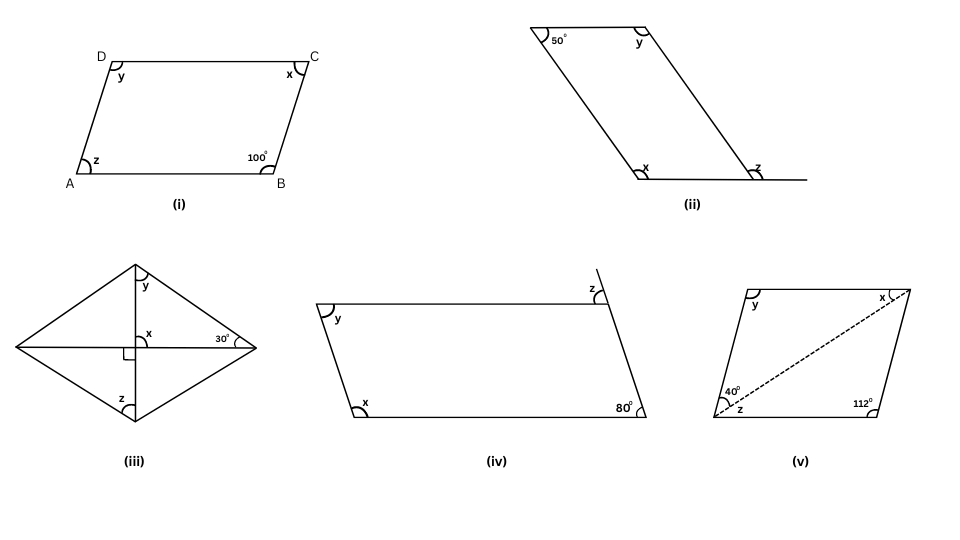
Answers:

(i) The figure is shown below:

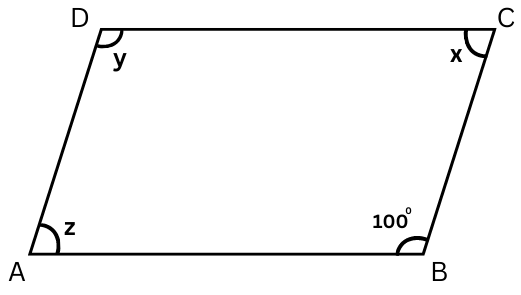
z + 100⁰ = 180⁰ (The adjacent angles in a parallelogram are supplementary)

or, z = 180⁰ – 100⁰

or, z = 80⁰

Now, y = 100⁰ (Opposite angles of a parallelogram are equal)

Also, x = z = 80⁰ (Opposite angles of a parallelogram are equal)

Summary: x = 80⁰, y = 100⁰ and z = 80⁰.

(ii) The figure is shown below:

50⁰ + x = 180⁰ (The adjacent angles in a parallelogram are supplementary)

or, x = 180⁰ – 50⁰

or, x = 130⁰

Now, y = x = 130⁰ (Opposite angles of a parallelogram are equal)

Also, z = x = 130⁰ (Equal corresponding angles because the opposite sides of the parallelogram are parallel)

Summary: x = 130⁰, y = 130⁰, z = 130⁰.

(iii) The figure is shown below:

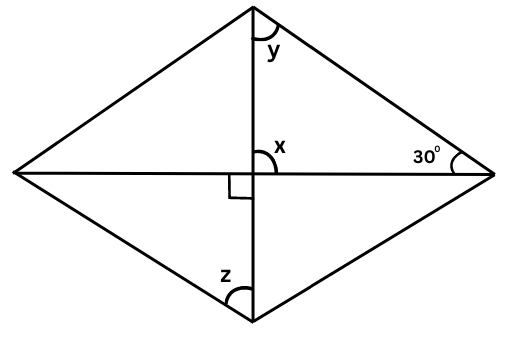
x = 90⁰ (Vertically opposite angles)

Now, x + y + 30⁰ = 180⁰ (Sum of angles of a triangle = 180⁰)

or, 90⁰ + y + 30⁰ = 180⁰

or, y = 180⁰ – 120⁰ = 60⁰

Also, z = y = 60⁰ (Equal alternate angles because the opposite sides of the parallelogram are parallel)

Summary: x = 90⁰, y = 60⁰, z = 60⁰.

(iv) The figure is shown below:

y = 80⁰ (Vertically opposite angles)

z = y = 80⁰ (Equal alternate angles because the opposite sides of the parallelogram are parallel)

x + y = 180⁰ (The adjacent angles in a parallelogram are supplementary)

or, x + 80⁰ = 180⁰

or, x = 180⁰ – 80⁰ = 100⁰

Summary: x = 100⁰, y = 80⁰, z = 80⁰.

(v) The figure is shown below:

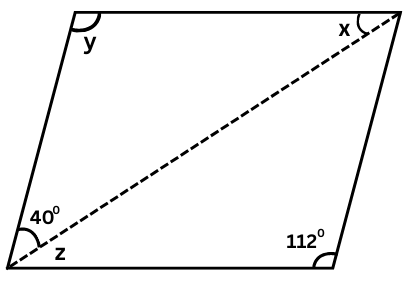
y = 112⁰ (Vertically opposite angles)

40⁰ + z + 112⁰ = 180⁰ (The adjacent angles in a parallelogram are supplementary)

or, z + 152⁰ = 180⁰

or, z = 180⁰ – 152⁰ = 28⁰

x = z = 28⁰ (Equal alternate angles because the opposite sides of the parallelogram are parallel)

Summary: x = 28⁰, y = 112⁰, z = 28⁰.

3. Can a quadrilateral ABCD be a parallelogram if

(i) ∠D + ∠B = 180°?                               (ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?

(iii) ∠A = 70° and ∠C = 65°?

Answers:

(i) ∠D + ∠B = 180°?

Quadrilateral ABCD is a parallelogram if opposite angles are equal and sum of adjacent angles are equal = 180⁰.

Here ∠D and ∠B are opposite angles in a parallelogram, so they have to be equal.

Since ∠D + ∠B = 180°, ∠D = ∠B = 90⁰

It is easy to see that ∠A and ∠C are both = 90⁰.

This gives us a rectangle.

Therefore, there may or may not be a parallelogram for the given condition. If there is a parallelogram it has to be a rectangle.

(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?

In a parallelogram opposite sides are equal. In this quadrilateral ABCD, AB = DC = 8 cm which satisfies the condition. But, AD = 4 cm and BC = 4.4 cm are not equal which does not satisfy the above condition. Therefore, in this case quadrilateral ABCD cannot be a parallelogram.

(iii) ∠A = 70° and ∠C = 65°?

In a parallelogram opposite angles are equal. ∠A = 70° and ∠C = 65⁰, which does not satisfy the above condition. Therefore, in this case quadrilateral ABCD cannot be a parallelogram.

Summary: For quadrilateral ABCD: if (i) ∠D + ∠B = 180°, there may or may not be a parallelogram. If there is a parallelogram it has to be a rectangle. If (ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm, quadrilateral ABCD cannot be a parallelogram. If (iii) ∠A = 70° and ∠C = 65°, quadrilateral ABCD cannot be a parallelogram.

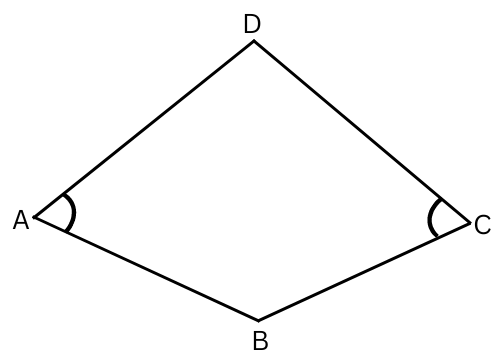
4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

Answer:

The following quadrilateral ABCD has opposite angles ∠A and ∠C of equal measure, but is not a quadrilateral.

5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.

Answer:

Let the two adjacent angles of a parallelogram be 3x and 2x.

The adjacent angles in a parallelogram are supplementary.

So, 3x + 2x = 180⁰

or, 5x = 180⁰

or, x = 180/5 = 36⁰

Then 3x = 108⁰ and 2x = 72⁰.

Opposite angles of a parallelogram are equal.

Therefore, the angle opposite to 3x = 108⁰ and the angle opposite to 2x = 72⁰.

Summary: The measures of the four angles of the parallelogram are 108⁰, 72⁰, 108⁰ and 72⁰.

6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Answer:

Let the measure of each adjacent angle be x.

The adjacent angles in a parallelogram are supplementary.

x + x = 180⁰

or, 2x = 180⁰

or, x = 180/2 = 90⁰

Opposite angles of a parallelogram are equal.

Therefore, the other two angles also = 90⁰.

Summary: Therefore, the measure of each angle of the parallelogram = 90⁰. This suggests that the parallelogram is a rectangle or a square.

7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

Answer:

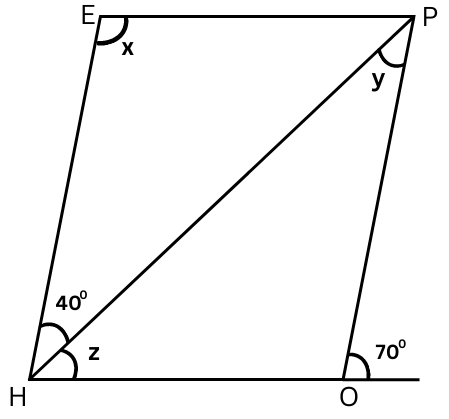
Answer:

In parallelogram HOPE,

∠H = ∠O = 70⁰ (Corresponding angles because HE ∥ OP)

z + 40⁰ = 70⁰

or, z = 70⁰ – 40⁰ = 30⁰

∠H + ∠E = 180⁰ (The adjacent angles in a parallelogram are supplementary)

or, 70⁰ + x = 180⁰

or, x = 180⁰ – 70⁰ = 110⁰

Also, y = 40⁰ (Alternate angles are equal)

Summary: In parallelogram HOPE, x = 110⁰, y = 40⁰ and z = 30⁰.

8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

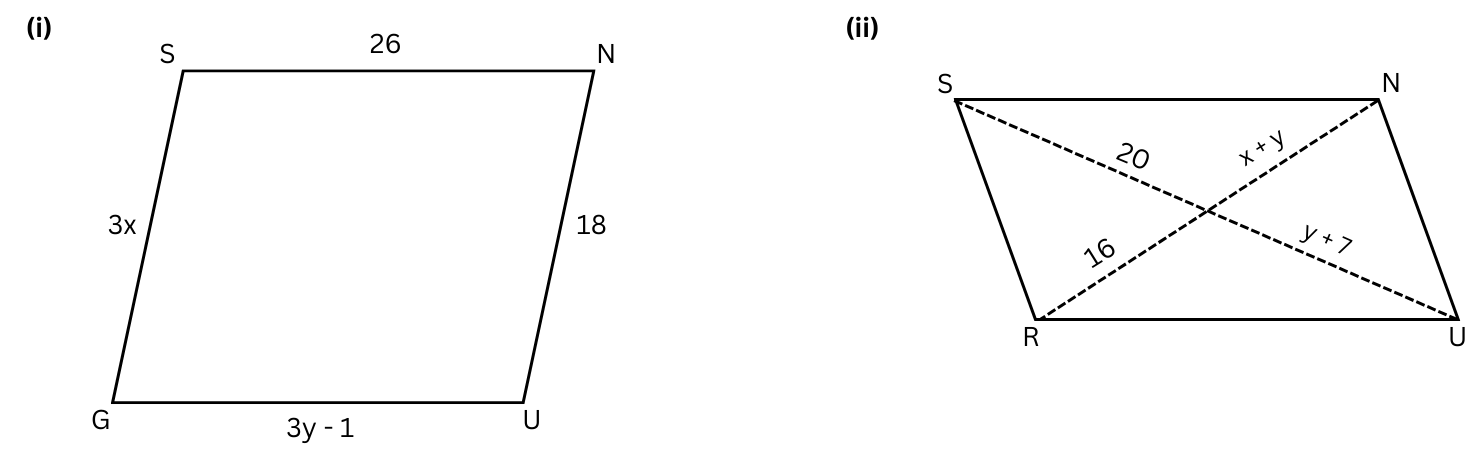
Answers:

(i) In parallelogram GUNS opposite sides are parallel.

Therefore,

3x = 18 or x = 18/3 = 6

and, 3y – 1 = 26

or, 3y = 26 + 1

or, 3y = 27

or y = 27/3 = 9

In parallelogram GUNS, x = 6 and y = 9.

(ii) In parallelogram RUNS, the diagonals bisect each other.

Therefore,

y + 7 = 20 or, y = 20 – 7 = 13

Also, x + y = 16

or, x + 13 = 16

or, x = 16 – 13 = 3

In parallelogram RUNS, x = 3 and y = 13.

Summary: (i) In parallelogram GUNS, x = 6 and y = 9. (ii) In parallelogram RUNS, x = 3 and y = 13.

9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.

Answer:

In parallelogram RISK,

∠K + ∠ISK = 180⁰ (Adjacent angles in a parallelogram are supplementary)

or, 120⁰ + ∠ISK = 180⁰

or, ∠ISK = 180⁰ – 120⁰

or, ∠ISK = 60⁰

In parallelogram CLUE,

∠CEU = ∠L (Opposite angles in a parallelogram are equal)

or, ∠CEU = 70⁰

In △EOS sum of all three angles = 180⁰.

Therefore,

x + 60⁰ + 70⁰ = 180⁰

or, x + 130⁰ = 180⁰

or, x = 180⁰ – 130⁰

or, x = 50⁰

Summary: The value of x = 50⁰. We used the properties that adjacent angles in a parallelogram are supplementary, opposite angles in a parallelogram are equal and sum of all three angles in a triangle = 180⁰.

10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)

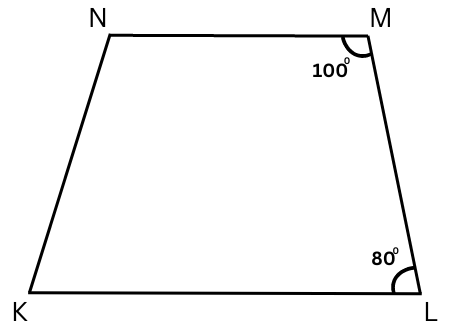
Answer: ∠L and ∠M are adjacent interior angles, ML is the transversal and ∠L + ∠M = 80⁰ + 100⁰ = 180⁰. Therefore, we can say that NM ∥ KL. The other two sides are not parallel. Hence, we can say that in the figure only one pair of sides are parallel and it is a trapezium.

11. Find m∠C in Fig 3.33 if AB ∥ DC.

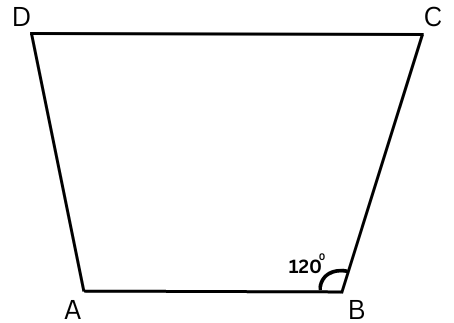
Answer: If AB ∥ DC, and ∠B + ∠C = 180⁰ because they are adjacent interior angles. So, 120⁰ + ∠C = 180⁰ or m∠C = 180⁰ – 120⁰ = 60⁰.

12. Find the measure of ∠P and ∠S if SP ∥ RQ in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)

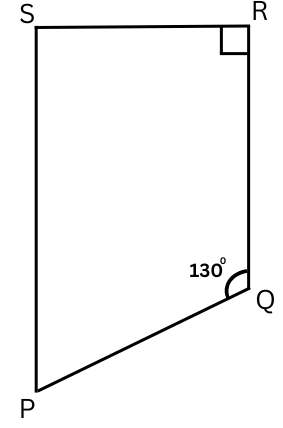
Answer:

Since SP ∥ RQ , we have:

 ∠P + ∠Q = 180⁰

or ∠P = 180⁰ – 130⁰

or ∠P = 50⁰.

We also have ∠S + ∠R = 180⁰

or ∠S = 180⁰ – 90⁰

or ∠S = 90⁰.

Alternative Method: The sum of all interior angles in a quadrilateral = 360⁰.

Therefore,

∠P + ∠Q + ∠S + ∠R = 360⁰

or, ∠P + 130⁰ + 90⁰ + 90⁰ = 360⁰

or, ∠P + 310⁰ = 360⁰

or, ∠P = 360⁰ – 310⁰

or, ∠P = 50⁰

Summary: The measure of ∠P = 50⁰ and measure of ∠S = 90⁰. You can use the alternate method that the sum of all interior angles in a quadrilateral = 360⁰ to find the magnitude of ∠P = 50⁰.

Solutions to Exercise 3.4 (Page No 35) of NCERT Class 8 Math Chapter 3 Understanding Quadrilaterals –

1. State whether True or False.

(a) All rectangles are squares.

Answer: False. Only a specific kind of rectangle where all sides are equal is called a square. Hence, all rectangles are not squares.

(b) All rhombuses are parallelograms.

Answer: True. A rhombus is a special case of a parallelogram with all sides equal. Therefore, all rhombuses are parallelograms.

(c) All squares are rhombuses and also rectangles.

Answer: True. A square is a specific kind of rhombus with each interior angle = 90⁰. Hence, all squares are rhombuses. A square is a specific kind of rectangle with all sides equal. Hence, all squares are rectangles.

(d) All squares are not parallelograms.

Answer: False. A square is a specific type of parallelogram with all sides equal. Hence, all squares are parallelograms.

(e) All kites are rhombuses.

Answer: False. A kite becomes a rhombus only when all sides are equal. Hence, all kites are not rhombuses.

 (f) All rhombuses are kites.

Answer: True. A rhombus is a specific type of kite in which all sides equal and diagonals bisect each other. Hence, all rhombuses are kites.

(g) All parallelograms are trapeziums.

Answer: False. Parallelograms have both pairs of opposite sides parallel. A trapezium has only one pair of opposite sides parallel. Hence, all parallelograms are not trapeziums.

(h) All squares are trapeziums.

Answer: False. Squares have opposite sides parallel and all sides equal. A trapezium has only one pair of opposite sides parallel. Hence, all squares are not trapeziums.

2. Identify all the quadrilaterals that have.

(a) four sides of equal length                                (b) four right angles

Answers:

(a) Rhombus and square have four sides of equal length.

(b) Square and rectangle have four right angles.


3. Explain how a square is

(i) a quadrilateral                  (ii) a parallelogram                   (iii) a rhombus                (iv) a rectangle

Answers:

(i) a quadrilateral: A square isa quadrilateral because it has four sides.

(ii) a parallelogram: A square is a parallelogram because the opposite sides are parallel.

(iii) a rhombus: A square is a rhombus because all sides are equal and diagonals are perpendicular bisectors of each other.

(iv) a rectangle: A square is a rectangle because all interior angles are = 90⁰ and opposite sides are equal.

Summary: A square is (i) a quadrilateral because it has four sides.(ii) a parallelogram because opposite sides are parallel.(iii) a rhombus because all sides are equal and diagonals are perpendicular bisectors of each other. (iv) a rectangle because all interior angles are = 90⁰ and opposite sides are equal.

4. Name the quadrilaterals whose diagonals.

(i) bisect each other             (ii) are perpendicular bisectors of each other              (iii) are equal

Answer:

(i) bisect each other: The diagonals of a parallelogram, rhombus, rectangle and square bisect each other.

(ii) are perpendicular bisectors of each other: Rhombus and square.

(iii) are equal: The diagonals of a rectangle and square are equal.

5. Explain why a rectangle is a convex quadrilateral.

Answer: A rectangle is a convex quadrilateral because both the diagonals lie in the interior. Also in a rectangle, all four interior angles are = 90⁰. Since all angles in a rectangle are less than 180⁰, it satisfies the condition of a convex quadrilateral.

6. ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

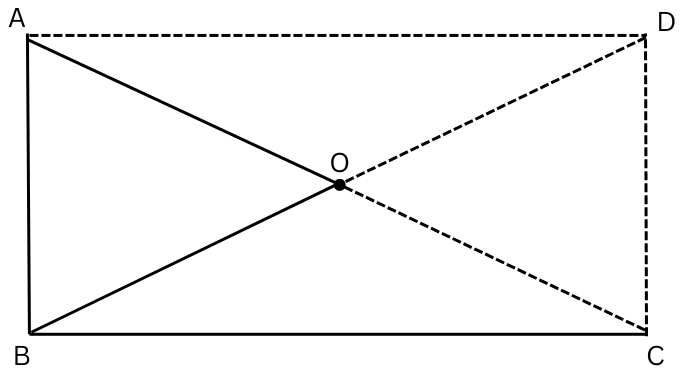
Answer:

AD and DC are drawn so that AB || DC and AD || BC and AB = DC and AD = BC.

Hence, ∠B = ∠C = ∠D = ∠A = 90⁰.

Therefore, ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are 90°.

The diagonals of a rectangle are equal and bisect each other.

Therefore,

AC = BD and AO = OC = BO = OD.

Hence, it is proved O is equidistant from A, B and C.

Summary: ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle.O is equidistant from A, B and C because O is the point of intersection of the diagonals of the rectangle ABCD. The diagonals are equal and bisect each other and so AO = OC = BO.

Important Questions from Previous NCERT Textbook:

Exercise 3.1 Page No: 41 (Old Textbook):

2. How many diagonals does each of the following have?

(a) A convex quadrilateral              (b) A regular hexagon            (c) A triangle

Answers:

(a) A convex quadrilateral has 2 diagonals. (b) A regular hexagon has 9 diagonals. (c) A triangle has 0 diagonals.

3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)

Answer: Look at the convex quadrilateral ABCD below:

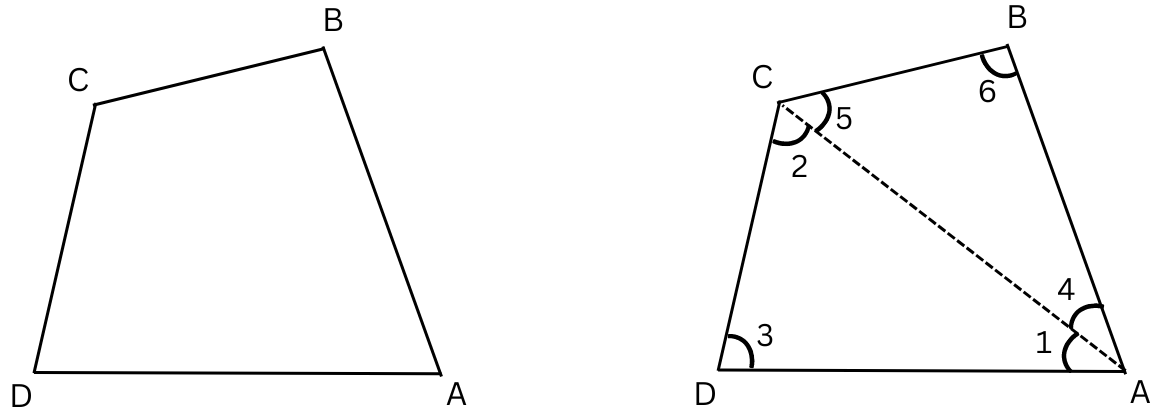
Join AC in ABCD.

ABCD = ΔADC + ΔABC

In ΔADC, ∠1 + ∠2 + ∠3 = 180⁰ and in ΔABC, ∠4 + ∠5 + ∠6 = 180⁰.

Therefore, in ABCD sum of angles = ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180⁰ + 180⁰= 360⁰.

Look at the concave quadrilateral ABCD below:

Join BD in ABCD,

ABCD = ΔBDA + ΔBDC

In ΔBDC, ∠1 + ∠2 + ∠3 = 180⁰ and in ΔBDA, ∠4 + ∠5 + ∠6 = 180⁰.

Therefore, in ABCD sum of angles = ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180⁰ + 180⁰= 360⁰.

Summary: The sum of the measures of the angles of a convex quadrilateral = 360⁰ and the sum of the measures of the angles of a non-convex quadrilateral also = 360⁰. This property holds for any quadrilateral because any quadrilateral can be divided into two triangles, each having sum of angles = 180⁰.

4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides?

(a) 7               (b) 8             (c) 10            (d) n

Answers:

From the information give in the above table we can develop a formulae for the angle sum of a polygon with n sides:

Angle sum of a polygon with n sides = (n – 2) × 180⁰

(a) 7

For n = 7, angle sum = (7 – 2) × 180⁰ = 5 × 180⁰ = 900⁰.

(b) 8  

For n = 8, angle sum = (8 – 2) × 180⁰ = 6 × 180⁰ = 1080⁰.

(c) 10

For n = 10, angle sum = (10 – 2) × 180⁰ = 8 × 180⁰ = 1440⁰.

(d) n

For n sides, angle sum = (n – 2) × 180⁰

Summary: The formulae for angle sum of a polygon with n sides = (n – 2) × 180⁰. Therefore: (a) For n = 7, angle sum = 900⁰, (b) for n = 8, angle sum = 1080⁰, (c) for n = 10, angle sum = 1440⁰ and (d) for n sides, angle sum = (n – 2) × 180⁰.

6. Find the angle measure of x in the following figures.

(a) The figure is shown below:

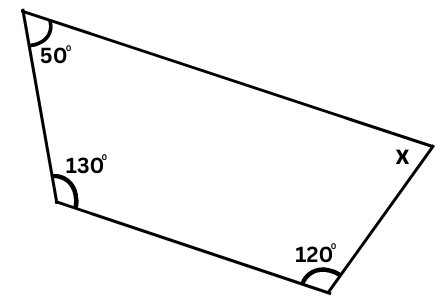
The figure has four sides, hence it is a quadrilateral.

Sum of all angles in a quadrilateral = 360⁰.

Therefore,

x + 50⁰ + 130⁰ + 120⁰ = 360⁰

or, x + 300⁰ = 360⁰

or, x = 360⁰ – 300⁰

or, x = 60⁰ (Answer)

(b) The figure is shown below:

The figure has four sides, hence it is a quadrilateral.

Sum of all angles in a quadrilateral = 360⁰.

One angle = 90⁰.

Therefore,

90⁰ + x + 70⁰ + 60⁰ = 360⁰

or, x + 220⁰ = 360⁰

or, x = 360⁰ – 220⁰

or, x = 140⁰ (Answer)

(c) The figure is shown below:

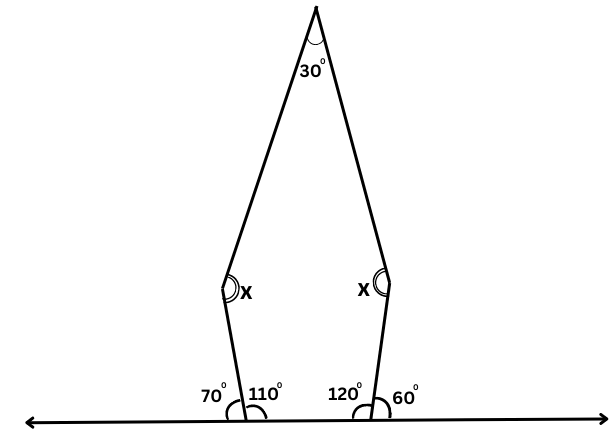
The figure has five sides, hence it is a pentagon.

The 70⁰ angle and the adjacent angle inside the polygon are supplementary.

So, 180⁰ – 70⁰ = 110⁰

The 60⁰ angle and the adjacent angle inside the polygon are supplementary.

So, 180⁰ – 60⁰ = 120⁰

Angle sum of a polygon with n sides = (n – 2) × 180⁰.

For a polygon with 5 sides = (5 – 2) × 180⁰ = 3 × 180⁰ = 540⁰.

Therefore,

110⁰ + 120⁰ + x + x + 30⁰ = 540⁰

or, 260⁰ + 2x = 540⁰

or, 2x = 540⁰ – 260⁰

or, 2x = 280⁰

or, x = 280/2 

or, x = 140⁰ (Answer)

(d) The figure is shown below:

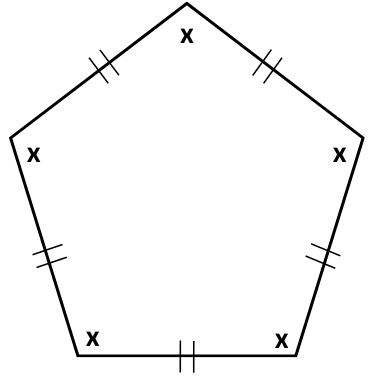
The figure has five sides, hence it is a pentagon.

Angle sum of a polygon with n sides = (n – 2) × 180⁰.

For a polygon with 5 sides = (5 – 2) × 180⁰ = 3 × 180⁰ = 540⁰.

Therefore,

x + x + x + x + x = 540⁰

or, 5x = 540⁰

or, x = 540/5

or, x = 108⁰ (Answer)

Summary: For figure (a) the value of x = 60⁰, for figure (b) the value of x = 140⁰, for figure (c) the value = 140⁰ and for figure (d) the value of x = 108⁰.

7. (a)

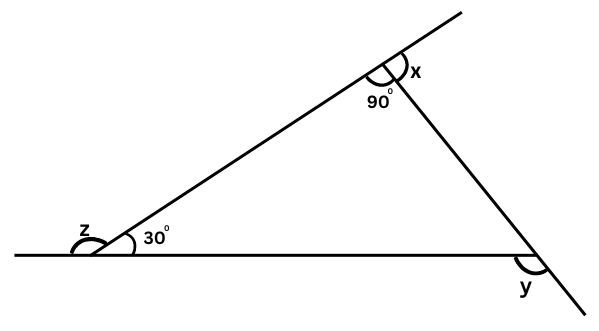
Find x + y + z

Answer:

(a) The angles z and 30⁰ are supplementary.

z + 30⁰ = 180⁰

or, z = 180⁰ – 30⁰ = 150⁰

The angles x and 90⁰ are supplementary.

x + 90⁰ = 180⁰

or, x = 180⁰ – 90⁰ = 90⁰

y is the exterior angle of the triangle and 30⁰ and 90⁰ are the two interior opposite angles.

y = 30⁰ + 90⁰ = 120⁰

x + y + z = 90⁰ + 120⁰ + 150⁰ = 360⁰

(b)

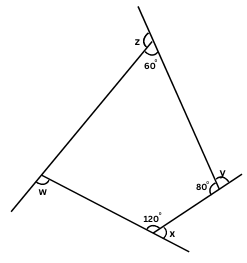
Find x + y + z + w

Answer:

The figure has four sides, hence it is a quadrilateral.

Sum of all angles in a quadrilateral = 360⁰.

Unknown fourth angle = 360⁰ – 120⁰ – 80⁰ – 60⁰ = 100⁰

z and 60⁰ are supplementary.

z + 60⁰ = 180⁰

or, z = 180⁰ – 60⁰ = 120⁰

y and 80⁰ are supplementary.

y + 80⁰ = 180⁰

or, y = 180⁰ – 80⁰ = 100⁰

x and 120⁰ are supplementary.

x + 120⁰ = 180⁰

or, x = 180⁰ – 120⁰ = 60⁰

w and 100⁰ are supplementary.

w + 100⁰ = 180⁰

or, w = 180⁰ – 100⁰ = 80⁰

Therefore, x + y + z + w = 60⁰ + 100⁰ + 120⁰ + 80⁰ = 360⁰.

Summary: The values of (a) x + y + z = 360⁰ and (b) x + y + z + w = 360⁰.

Extra Questions to Complement Solutions to NCERT Class 8 Mathematics Chapter 3 Understanding Quadrilaterals:

Very Short Answer Type Questions:

1. The diagonals of a parallelogram bisect each other but are not equal. Which specific types of parallelograms can you rule out based on this condition?
Answer:
You can rule out square, rectangle and rhombus. The diagonals in a square, rectangle or rhombus are equal and bisect each other.

2. You are given star-shaped polygon. What kind of polygon is it?
Answer:
The star-shaped polygon is a concave polygon.

3. Calculate the sum of interior angles in a hexagon.
Answer:
The sum of interior angles for a polygon of n sides = (n – 2) × 180⁰. Therefore, the sum of interior angles in a hexagon = (6 – 2) × 180⁰ = 4 × 180⁰ = 720⁰.

4. Are the measures of the exterior angles in a regular hexagon equal? Why?
Answer:
In a regular hexagon the measure of interior angles are equal. Since interior angle + exterior angle = 180⁰, all the exterior angles are also equal.

5. Name a quadrilateral that has one line of symmetry.
Answer:
The kite is a quadrilateral that has one line of symmetry.

6. Given the length of one side of a parallelogram = 5 cm can you find the length of all sides?
Answer:
No. In a parallelogram only opposite sides are equal.If we are given the length of one side = 5 cm, we can only find the length of the opposite side. You cannot find the length of the other two sides.

7. Name the quadrilaterals whose diagonals are equal in length and bisect each other.
Answer:
Square and rectangle are the quadrilaterals whose diagonals are equal in length and bisect each other.

8. Only three sides of a quadrilateral are equal. The length of the fourth side is known. Is it a square?
Answer:
It may not be a square. The interior angles of the quadrilateral may not be 90⁰, in which case it will not be a square.

9. Explain why the sum of interior angles in any quadrilateral is always 360⁰.
Answer:
Any quadrilateral can be divided into two triangles by drawing a diagonal. Sum of the angles of each triangle = 180⁰. Sum of the angles of both triangles which make up the quadrilateral = 180⁰ + 180⁰ = 360⁰.

10. Name the quadrilaterals which have a line of symmetry along a diagonal.
Answer:
Rhombus, square and kite are the quadrilaterals which have a line of symmetry along a diagonal. Rhombus and square are symmetric about both diagonals. Kite is symmetric about one diagonal.

Multiple Choice Questions (MCQ):

1. What can you say about the diagonals in a kite:

(a) They bisect each other.
(b) Only one of diagonals bisects the other.
(c) The diagonals do not bisect each other
(d) Whether the diagonals bisect each other depends on the length of the sides of the kite.

Answer: Correct answer: (b) Only one of diagonals bisects the other.

2. The diagonals of a parallelogram:

(a) Bisect each other at right angles.
(b) Bisect each other and are equal.
(c) Do not bisect each other.
(d) Bisect each other and are not equal.

Answer: Correct answer: (d) Bisect each other and are not equal.

3. The perimeter of a rhombus is 40 cm. Is it possible to find the length of each side?

(a) Yes it is possible.
(b) No you need extra information.
(c) It is possible for this rhombus, but not for other rhombuses.
(d) It is not possible for this rhombus, but might be possible for other rhombuses.

Answer: Correct answer:(a) Yes it is possible.

All sides in a rhombus are equal. Therefore, each side = 40/4 = 10 cm.

4. A diagonal of a square is drawn. The resulting two triangles:

(a) Are congruent
(b) Have equal area
(c) Are both congruent and have equal area
(d) None of the above

Answer: Correct answer: (c) Are both congruent and have equal area.

5. A trapezium has:

(a) One pair of parallel sides.
(b) One pair of parallel lines and two equal sides.
(c) Two pairs of parallel sides.
(d) One pair of parallel lines and two pairs of equal sides

Answer: Correct answer:(a) One pair of parallel lines.

Short and Long Answer Type Questions:

1. Find the measure of x in the following figure:

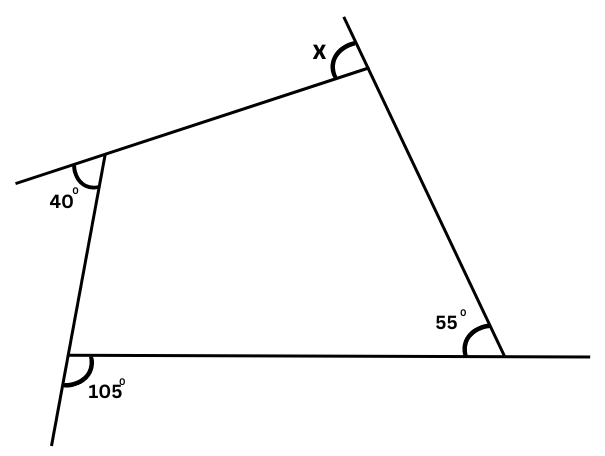
Answer: The figure is shown below:

Interior and exterior angles form a supplementary pair.

y + 55⁰ = 180⁰

or, y = 180⁰ – 55⁰ = 125⁰

Sum of all the measures of external angles in a polygon = 360⁰.

Therefore,

105⁰ + 40⁰ + 125⁰ + x = 360⁰

or, 270⁰ + x = 360⁰

or, x = 360⁰ – 270⁰

or, x = 90⁰ (Answer)

2. What is the value of x in the kite below? Given: ∠ABD = 45⁰.

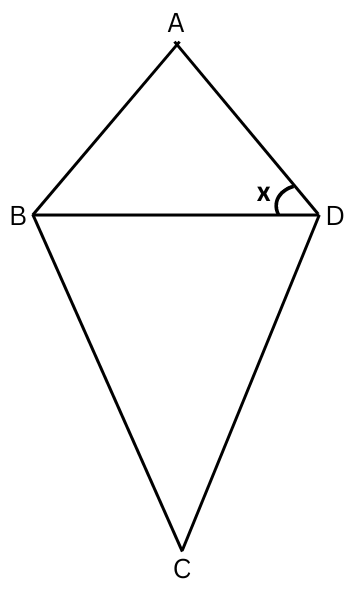
Answer:

In △ABD, ∠ABD = 45⁰.

Since ABCD is a kite, AB = AD.

Therefore, ∠ABD = ∠ADB (△ABD is isosceles triangle) or, x = ∠ADB = 45⁰.

3. Find the value of x in parallelogram ABCD.

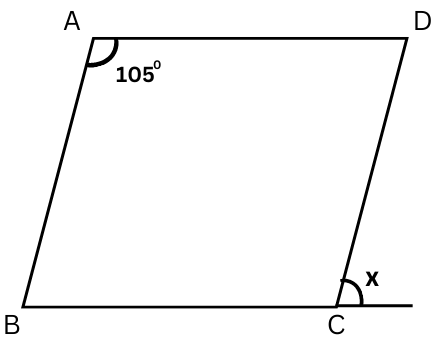
Answer:

Given: ∠BAD = 105⁰.

Opposite angles in a parallelogram are equal.

Therefore, ∠BCD = 105⁰.

Interior and exterior angles are supplementary.

∠BCD + x = 180⁰.

or, 105⁰ + x = 180⁰

or, x = 180⁰ – 105⁰

or, x = 75⁰ (Answer)

4. In parallelogram ABCD, the length of side AB is 10 cm, and the length of side BC is 12 cm. If the measure of ∠B is 65⁰, find the length of side AD and the measure of angles A, C, and D.

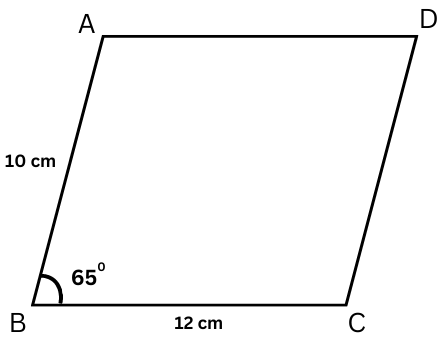
Answer:

Opposite sides in a parallelogram are equal.

Therefore, AD = BC = 12 cm.

The adjacent interior angles in a parallelogram are supplementary.

Therefore,

∠A + ∠B = 180⁰

or, ∠A + 65⁰ = 180⁰

or, ∠A = 180⁰ – 65⁰

or, ∠A = 115⁰

Opposite angles in a parallelogram are equal.

Therefore,

∠D = ∠B = 65⁰.

and ∠C = ∠A = 115⁰

5. Find the length of the diagonal of a square of side 5 cm.

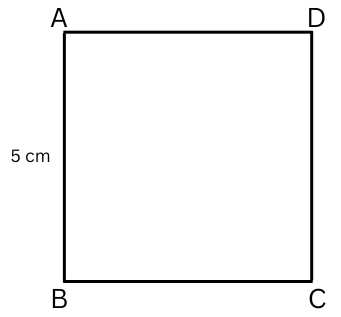
Answer: The angles of a square are all = 90⁰ and all sides are equal.

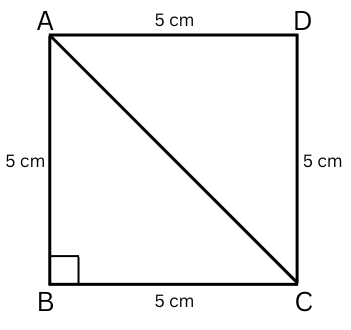
Therefore, using Pythagoras’ theorem:

AB² + BC² = AC²

or, AC² = AB² + BC²

or, AC² = 5² + 5²

or, AC² = 25 + 25

or, AC² = 50

or AC = 7.07 (Answer)

6. The perimeter of a parallelogram is 36 cm, and the length of one side is 8 cm. Find the length of the other side.

Answer: Let the other side be x.

Opposite sides in a parallelogram are equal.

Perimeter of a rectangle = sum of all four sides.

Therefore,

2(x + 8) = 36

or, 2x + 16 = 36

or, 2x = 36 – 16

or, 2x = 20

or, x = 10

Therefore, the length of the other side = 10 cm.

7. Calculate the length of diagonal BD of a rhombus with one side = 5 cm and diagonal AC = 6 cm.

Answer: The figure is shown below:

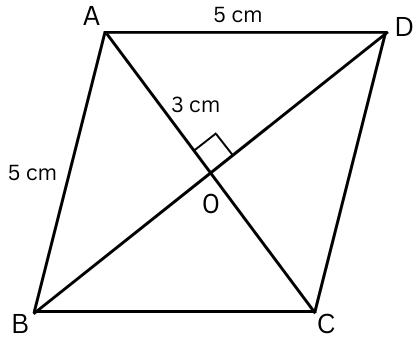
All sides of the rhombus are equal = 5 cm.

The diagonals bisect each other at 90⁰.

Therefore,

AO = OC = AC/2 = 6/2 = 3 cm.

Therefore, in △ AOD using Pythagoras Theorem:

AO² + OD² = AD²

or, 3² + OD² = 5²

or, OD² = 25 – 9

or, OD² = 16

or, OD = √16

or, OD = 4 cm

Therefore,

BD = 2OD = 8 cm. (since diagonals bisect each other)

Therefore, length of diagonal BD = 8 cm.

8. Look at the rectangle ABCD below. Can you find ∠BOC?

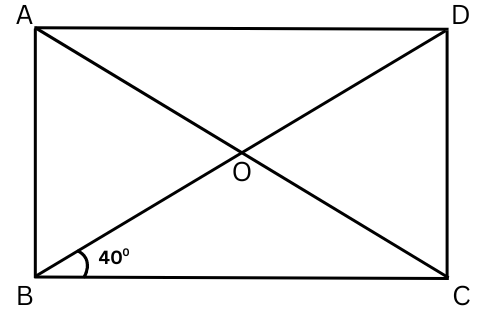
Answer: The figure is shown below:

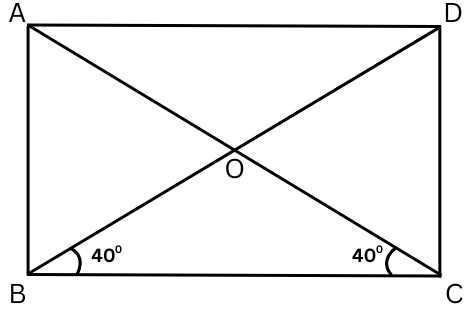
In a rectangle, diagonals are equal.

Therefore, AC = BD.

In a rectangle, diagonals bisect each other.

Therefore, BO = CO and △ BOC is an isosceles triangle.

Therefore, ∠OCB = ∠OBC = 40⁰.

In △ BOC sum of all angles = 180⁰.

∠BOC + ∠OCB + ∠OBC = 180⁰

or, ∠BOC + 40⁰ + 40⁰ = 180⁰

or, ∠BOC = 180⁰ – 80⁰

or, ∠BOC = 100⁰ (Answer)

9. Look at the parallelogram ABCD below. Can you find ∠BOC?

Answer:

In a parallelogram opposite sides are parallel.

Therefore, AD || BC and ∠ADB = ∠DBC = 30⁰ (alternate angles are equal)

In △ BOC sum of all angles = 180⁰.

∠BOC + ∠OCB + ∠OBC = 180⁰

or, ∠BOC + 40⁰ + 30⁰ = 180⁰

or, ∠BOC = 180⁰ – 70⁰

or, ∠BOC = 110⁰ (Answer)

10. Take a parallelogram ABCD in which ∠ABC = 120⁰. Extend the lines BA and CD. Then take any two points P and Q on BA extended and CD extended respectively. Join PQ. ∠QPA = 60⁰. Is DAPQ a parallelogram?

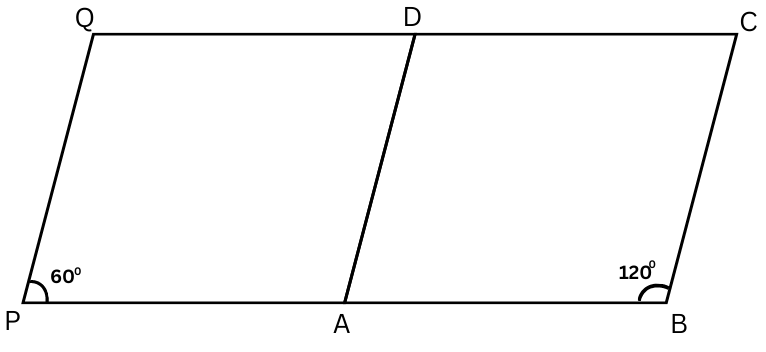
Answer:

In a parallelogram opposite sides are parallel.

Therefore, AD || BC and ∠DAB + ∠ABC = 180⁰ (sum of adjacent opposite angles = 180⁰)

or, ∠DAB + 120⁰ = 180⁰

or, ∠DAB = 180⁰ – 120⁰ = 60⁰

Now, ∠DAB = 60⁰ and ∠QPA = 60⁰ and PB is a transversal.

Therefore, we can say that PQ || AD. Also PA || QD because they are formed by extending the parallel lines BA and CD.

Hence it is proved that DAPQ is a parallelogram.

Fill in the Blanks:

(a) __________ is a polygon with 8 sides.

(b) In a convex polygon, all interior angles are __________ 180⁰.

(c) A __________ is a simple closed curve with 7 sides.

(d) A kite is a type of _________.

(e) The diagonals of a rhombus bisect each other at __________ angles.

Answers:

(a) Octagon is a polygon with 8 sides.

(b) In a convex polygon, all interior angles are less than 180⁰.

(c) A heptagon is a simple closed curve with 7 sides.

(d) A kite is a type of quadrilateral.

(e) The diagonals of a rhombus bisect each other at right angles.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 8 Mathematics Chapter 3 Understanding Quadrilaterals: