Welcome folks! When it comes to mastering Chapter 5, practice is essential. Our solutions to the exercise problems and a variety of extra questions are an excellent place to start. We advise that you work out the problems yourselves alongside studying our solutions. This ‘learning by doing’ approach helps in better understanding and retention of the material.
Solutions to Exercise 5.1 (Page No 58) of NCERT Class 8 Mathematics Chapter 5 Squares and Square Roots:
1. What will be the unit digit of the squares of the following numbers?
(i) 81 (ii) 272 (iii) 799 (iv) 3853
(v) 1234 (vi) 26387 (vii) 52698 (viii) 99880
(ix) 12796 (x) 55555
Answers:
When the digit in the unit’s place of a number is squared, the rightmost digit of the square will give us the required digit.
(i) 81
If a number has 1 in the unit’s place, then its square ends in 1 because 1 × 1 = 1.
Since 81 has 1 in the unit’s place, the unit digit of the square of 81 is 1.
(ii) 272
If a number has 2 in the unit’s place, then its square ends in 4 because 2 × 2 = 4.
Since 272 has 2 in the unit’s place, the unit digit of the square of 272 is 4.
(iii) 799
If a number has 9 in the unit’s place, then its square ends in 1. We have 9 × 9 = 81 and we take the rightmost digit 1.
Since 799 has 9 in the unit’s place, the unit digit of the square of 799 is 1.
(iv) 3853
If a number has 3 in the unit’s place, then its square ends in 9 because 3 × 3 = 9.
Since 3853 has 3 in the unit’s place, the unit digit of the square of 3853 is 9.
(v) 1234
If a number has 4 in the unit’s place, then its square ends in 6. We have 4 × 4 = 16 and we take the rightmost digit 6.
Since 1234 has 4 in the unit’s place, the unit digit of the square of 1234 is 6.
(vi) 26387
If a number has 7 in the unit’s place, then its square ends in 9. We have 7 × 7 = 49 and we take the rightmost digit 9.
Since 26387 has 7 in the unit’s place, the unit digit of the square of 26387 is 9.
(vii) 52698
If a number has 8 in the unit’s place, then its square ends in 64. We have 8 × 8 = 64 and we take the rightmost digit 4.
Since 52698 has 8 in the unit’s place, the unit digit of the square of 52698 is 4.
(viii) 99880
If a number has 0 in the unit’s place, then its square ends in 0 because 0 × 0 = 0.
Since 99880 has 0 in the unit’s place, the unit digit of the square of 99880 is 0.
(ix) 12796
If a number has 6 in the unit’s place, then its square ends in 36. We have 6 × 6 = 36 and we take the rightmost digit 6.
Since 12796 has 6 in the unit’s place, the unit digit of the square of 12796 is 6.
(x) 55555
If a number has 5 in the unit’s place, then its square ends in 25. We have 5 × 5 = 25 and we take the rightmost digit 5. Since 55555 has 5 in the unit’s place, the unit digit of the square of 55555 is 5.
2. The following numbers are obviously not perfect squares. Give reason.
(i) 1057 (ii) 23453 (iii) 7928 (iv) 222222
(v) 64000 (vi) 89722 (vii) 222000 (viii) 505050
Answers:
(i) 1057
All perfect square numbers end with 0, 1, 4, 5, 6, 9 at the unit’s place. 1057 has 7 in the unit’s place and is obviously not a perfect square.
(ii) 23453
All perfect square numbers end with 0, 1, 4, 5, 6, 9 at the unit’s place. 23453 has 3 in the unit’s place and is obviously not a perfect square.
(iii) 7928
All perfect square numbers end with 0, 1, 4, 5, 6, 9 at the unit’s place. 7928 has 8 in the unit’s place and is obviously not a perfect square.
(iv) 222222
All perfect square numbers end with 0, 1, 4, 5, 6, 9 at the unit’s place. 222222 has 2 in the unit’s place and is obviously not a perfect square.
(v) 64000
Perfect square numbers can only have an even number of zeros at the end. 64000 has 3 zeroes at the end which is an odd number. So it is not a perfect square.
(vi) 89722
All perfect square numbers end with 0, 1, 4, 5, 6, 9 at the unit’s place. 89722 has 2 in the unit’s place and is obviously not a perfect square.
(vii) 222000
Perfect square numbers can only have an even number of zeros at the end. 222000 has 3 zeroes at the end which is an odd number. So it is not a perfect square.
(viii) 505050
Perfect square numbers can only have an even number of zeros at the end. 505050 has 1 zero at the end which is an odd number. So it is not a perfect square.
3. The squares of which of the following would be odd numbers?
(i) 431 (ii) 2826 (iii) 7779 (iv) 82004
Answers:
We know that the square of an odd number is always odd and the square of an even number is always even. Thus, the squares of (i)431 and (iii) 7779 would be odd numbers. Verification: The unit digit of the square of 431 is 1 (1 × 1 = 1) and the unit digit of 7779 is 1 (9 × 9 = 81), which is odd.
4. Observe the following pattern and find the missing numbers.
112 = 121
1012 = 10201
10012 = 1002001
1000012 = 1 ……. 2 ……… 1
100000012 = ………………..
Answer:
The above pattern indicates that the square of the given number has the same number of zeros before and after digit 2 as the given number has, and the digit 1 lies at both ends.
Therefore, 1000012 = 10000200001 and 100000012 = 100000020000001
5. Observe the following pattern and supply the missing numbers.
112 = 121
1012 = 10201
101012 = 102030201
10101012 = ………………………
…………2 = 10203040504030201
Answer:
The above pattern indicates the square of the given number has an odd number of digits and is symmetric about the middle digit.
Therefore,
10101012 = 1020304030201 and 1010101012 = 10203040504030201
6. Using the given pattern, find the missing numbers.
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 = 132
42 + 52 + _2 = 212
5 + _ 2 + 302 = 312
6 + 72 + _ 2 = __ 2
Answers:
The third number is the result of multiplying the first two numbers, and the fourth number is found by adding 1 to the third number.
Find the missing numbers below:
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 = 132
42 + 52 + 202 = 212
5 + 62 + 302 = 312
6 + 72 + 422 = 432
7. Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
Answer: We know that the sum of the first n odd natural numbers is n2. Therefore, for the first 5 numbers odd natural numbers, sum = 52 = 25.
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
Answer: We know that the sum of the first n odd natural numbers is n2. Therefore, for the first 10 numbers odd natural numbers, sum = 102 = 100.
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Answer: We know that the sum of the first n odd natural numbers is n2. Therefore, for the first 12 odd natural numbers, sum = 122 = 144.
8. (i) Express 49 as the sum of 7 odd numbers.
We know that the sum of the first n odd natural numbers is n2.
In this case, n2 = 49 or n = 7.
The first 7 odd numbers are 1, 3, 5, 7, 9, 11, 13.
Hence, sum: 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49.
(ii) Express 121 as the sum of 11 odd numbers.
We know that the sum of the first n odd natural numbers is n2.
If 121 is the sum, then n2 = 121 or n = 11.
The first 11 odd numbers are 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21.
Hence, sum: 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 = 121.
Summary: (i)49 expressed as the sum of 7 odd numbers is: 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49. (ii) 121 expressed as the sum of 11 odd numbers is: 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 = 121.
9. How many numbers lie between squares of the following numbers?
(i) 12 and 13 (ii) 25 and 26 (iii) 99 and 100
Answers:
(i) 12 and 13
In general, between n2 and (n + 1)2 there are 2n numbers.
Therefore, between 122 and 132 there are 2 × 12 = 24 numbers.
(ii) 25 and 26
In general, between n2 and (n + 1)2 there are 2n numbers.
Therefore, between 252 and 262 there are 2 × 25 = 50 numbers.
(iii) 99 and 100
In general, between n2 and (n + 1)2 there are 2n numbers.
Therefore, between 992 and 1002 there are 2 × 99 = 198 numbers.
Summary: Between (i) 12 and 13 there are 24 numbers, between (ii) 25 and 26 there are 50 numbers and between (iii) 99 and 100 there are 198 numbers.
Solutions to Exercise 5.2 (Page No 60) of NCERT Class 8 Mathematics Chapter 5 Squares and Square Roots:
1. Find the square of the following numbers.
(i) 32 (ii) 35 (iii) 86 (iv) 93
(v) 71 (vi) 46
Answers:
(i) 32
322 = (30 + 2)2
= 30(30 + 2) + 2(30 + 2)
= 302 + 30 × 2 + 2 × 30 + 22
= 900 + 60 + 60 + 4
= 1024 (Answer)
(ii) 35
352 = (30 + 5)2
= 30(30 + 5) + 5(30 + 5)
= 302 + 30 × 5 + 5 × 30 + 52
= 900 + 150 + 150 + 25
= 1225 (Answer)
(iii) 86
862 = (80 + 6)2
= 80(80 + 6) + 6(80 + 6)
= 802 + 80 × 6 + 6 × 80 + 62
= 6400 + 480 + 480 + 36
= 7396 (Answer)
(iv) 93
932 = (90 + 3)2
= 90(90 + 3) + 3(90 + 3)
= 902 + 90 × 3 + 3 × 90 + 32
= 8100 + 270 + 270 + 9
= 8649 (Answer)
(v) 71
712 = (70 + 1)2
= 70(70 + 1) + 1(70 + 1)
= 702 + 70 + 70 + 1
= 4900 + 140 + 1
= 5041 (Answer)
(vi) 46
462 = (40 + 6)2
= 40(40 + 6) + 6(40 + 6)
= 402 + 40 × 6 + 6 × 40 + 62
= 1600 + 240 + 240 + 36 = 2116 (Answer)
2. Write a Pythagorean triplet whose one member is.
(i) 6 (ii) 14 (iii) 16 (iv) 18
Answers:
(i) 6
For any natural number m > 1, we have 2m, m2 – 1 and m2 + 1 form a Pythagorean triplet.
Let us take 2m = 6.
Then m = 3.
m2 – 1 = 32 – 1 = 9 – 1 = 8.
and m2 + 1 = 32 + 1 = 9 + 1 = 10.
Therefore, the Pythagorean triplet is 6, 8, 10.
(ii) 14
For any natural number m > 1, we have 2m, m2 – 1 and m2 + 1 form a Pythagorean triplet.
Let us take 2m = 14.
Then m = 7.
m2 – 1 = 72 – 1 = 49 – 1 = 48.
and m2 + 1 = 72 + 1 = 49 + 1 = 50.
Therefore, the Pythagorean triplet is 14, 48, 50.
(iii) 16
For any natural number m > 1, we have 2m, m2 – 1 and m2 + 1 form a Pythagorean triplet.
Let us take 2m = 16.
Then m = 8.
m2 – 1 = 82 – 1 = 64 – 1 = 63.
and m2 + 1 = 82 + 1 = 64 + 1 = 65.
Therefore, the Pythagorean triplet is 8, 63, 65.
(iv) 18
For any natural number m > 1, we have 2m, m2 – 1 and m2 + 1 form a Pythagorean triplet.
Let us take 2m = 18.
Then m = 9.
m2 – 1 = 92 – 1 = 81 – 1 = 80.
and m2 + 1 = 92 + 1 = 81 + 1 = 82.
Therefore, the Pythagorean triplet is 18, 80, 82.
Solutions to Exercise 5.3 (Page No 64) of NCERT Class 8 Mathematics Chapter 5 Squares and Square Roots:
1. What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801 (ii) 99856 (iii) 998001 (iv) 657666025
Answers:
(i) 9801
If the square of a number ends with 1, the unit digit of the square root is either 1 (1 × 1 = 1) or 9 (9 × 9 = 81). Since 9801 ends with the digit 1, the possible ‘one’s’ digits of the square root are 1 or 9.
(ii) 99856
If the square of a number ends with 6, the unit digit of the square root is either 4 (4 × 4 = 16) or 6 (6 × 6 = 36). Since 99856 ends with the digit 6, the possible ‘one’s’ digits of the square root are 4 or 6.
(iii) 998001
If the square of a number ends with 1, the unit digit of the square root is either 1 (1 × 1 = 1) or 9 (9 × 9 = 81). Since 998001 ends with the digit 1, the possible ‘one’s’ digits of the square root are 1 or 9.
(iv) 657666025
If the square of a number ends with 5, the unit digit of the square root is 5 (5 × 5 = 25). Since 657666025ends with the digit 5, the ‘one’s’ digits of the square root is 5.
Summary: (i) Since 9801 ends with the digit 1, the ‘one’s’ digit of the square root is 1 or 9. (ii) Since 99856 ends with the digit 6, the ‘one’s’ digit of the square root is 4 or 6. (iii) Since 998001 ends with the digit 1, the ‘one’s’ digit of the square root is 1 or 9. (iv) Since 657666025ends with the digit 5, the ‘one’s’ digit of the square root is 5.
2. Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153 (ii) 257 (iii) 408 (iv) 441
Answers:
(i) 153
The numbers with 2, 3, 7 and 8 in the unit’s place are not perfect squares. Since 153 has 3 in the unit’s place it is not a perfect square.
(ii) 257
The numbers ending with 2, 3, 7 and 8 in the unit’s place are not perfect squares. Since 257 has 7 in the unit’s place it is not a perfect square.
(iii) 408
The numbers ending with 2, 3, 7 and 8 in the unit’s place are not perfect squares. Since 408 has 8 in the unit’s place it is not a perfect square.
(iv) 441
The numbers with 0, 1, 4, 5, 6 or 9 in the unit’s place must be perfect squares. Since 441 has 1 in the unit’s place it must be a perfect square. It is the square of the number 21.
Summary: (i) Since 153 has 3 in the unit’s place it is not a perfect square. (ii) Since 257 has 7 in the unit’s place it is not a perfect square. (iii) Since 408 has 8 in the unit’s place it is not a perfect square. (iv) Since 441 has 1 in the unit’s place it must be a perfect square.
3. Find the square roots of 100 and 169 by the method of repeated subtraction.
Answers:
(a) Square root of 100:
Every square number can be expressed as a sum of successive odd natural numbers starting from 1.
Therefore,
(i) 100 – 1 = 99, (ii) 99 – 3 = 96, (iii) 96 – 5 = 91, (iv) 91 – 7 = 84, (v) 84 – 9 = 75, (vi) 75 – 11 = 64, (vii) 64 – 13 = 51, (viii) 51 – 15 = 36, (ix) 36 – 17 = 19, (x) 19 – 19 = 0.
From 100 we have subtracted successive odd numbers and obtained 0 at the 10th step. Therefore, √100 = 10.
(b) Square root of 169:
Every square number can be expressed as a sum of successive odd natural numbers starting from 1.
Therefore,
(i) 169 – 1 = 168, (ii) 168 – 3 = 165, (iii) 165 – 5 = 160, (iv) 160 – 7 = 153, (v) 153 – 9 = 144, (vi) 144 – 11 = 133, (vii) 133 – 13 = 120, (viii) 120 – 15 = 105, (ix) 105 – 17 = 88, (x) 88 – 19 = 69, (xi) 69 – 21 = 48, (xii) 48 – 23 = 25, (xiii) 25 – 25 = 0. From 169 we have subtracted successive odd numbers and obtained 0 at the 13th step. Therefore, √169 = 13.
4. Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729 (ii) 400 (iii) 1764 (iv) 4096
(v) 7744 (vi) 9604 (vii) 5929 (viii) 9216
(ix) 529 (x) 8100
Answers:
(i) 729
The prime factorisation of 729 is shown below:
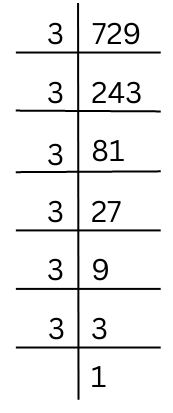
Therefore, the prime factorisation of 729 = 3 × 3 × 3 × 3 × 3 × 3.
By pairing the prime factors we get,
729 = 3 × 3 × 3 × 3 × 3 × 3 = 32 × 32 × 32 = (3 × 3 × 3)2
So, √729 = 3 × 3 × 3 = 27.
Summary: Using the prime factorisation method we get the square root of 729 = 27.
(ii) 400
The prime factorisation of 400 is shown below:

Therefore, the prime factorisation of 400 = 2 × 2 × 2 × 2 × 5 × 5.
By pairing the prime factors we get,
400 = 2 × 2 × 2 × 2 × 5 × 5 = 22 × 52 × 52 = (2 × 5 × 5)2
So, √400 = 2 × 2 × 5 = 20.
Summary: Using the prime factorisation method we get the square root of 400 = 20.
(iii) 1764
The prime factorisation of 1764 is shown below:

Therefore, the prime factorisation of 1764 = 2 × 2 × 3 × 3 × 7 × 7.
By pairing the prime factors we get,
1764 = 2 × 2 × 3 × 3 × 7 × 7 = 22 × 32 × 72 = (2 × 3 × 7)2
So, √1764 = 2 × 3 × 7 = 42.
Summary: Using the prime factorisation method we get the square root of 1764 = 42.
(iv) 4096
The prime factorisation of 4096 is shown below:

Therefore, the prime factorisation of 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
By pairing the prime factors we get,
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 22 × 22 × 22 × 22 × 22 × 22 = (2 × 2 × 2 × 2 × 2 × 2)2
So, √4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64.
Summary: Using the prime factorisation method we get the square root of 4096 = 64.
(v) 7744
The prime factorisation of 7744 is shown below:

Therefore, the prime factorisation of 7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11.
By pairing the prime factors we get,
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11 = 22 × 22 × 22 × 112 = (2 × 2 × 2 × 11)2
So, √7744 = 2 × 2 × 2 × 11 = 88.
Summary: Using the prime factorisation method we get the square root of 7744 = 88.
(vi) 9604
The prime factorisation of 9604 is shown below:
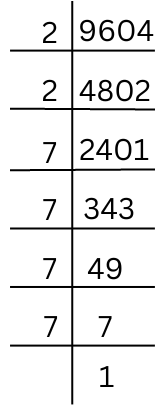
Therefore, the prime factorisation of 9604 = 2 × 2 × 7 × 7 × 7 × 7.
By pairing the prime factors we get,
9604 = 2 × 2 × 7 × 7 × 7 × 7 = 22 × 72 × 72 = (2 × 7 × 7)2
So, √9604 = 2 × 7 × 7 = 98.
Summary: Using the prime factorisation method we get the square root of 9604 = 98.
(vii) 5929
The prime factorisation of 5929 is shown below:
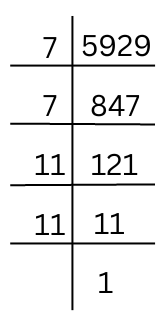
Therefore, the prime factorisation of 5929 = 7 × 7 × 11 × 11.
By pairing the prime factors we get,
5929 = 7 × 7 × 11 × 11 = 72 × 112 = (7 × 11)2
So, √5929 = 7 × 11 = 77.
Summary: Using the prime factorisation method we get the square root of 5929 = 77.
(viii) 9216
The prime factorisation of 9216 is shown below:
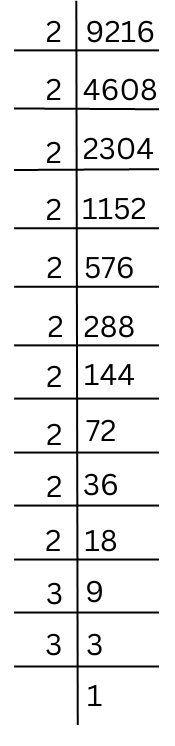
Therefore, the prime factorisation of 9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
By pairing the prime factors we get,
9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 = 22 × 22 × 22 × 22 × 22 = (2 × 2 × 2 × 2 × 2 × 3)2
So, √9216 = 2 × 2 × 2 × 2 × 2 × 3 = 96.
Summary: Using the prime factorisation method we get the square root of 9216 = 96.
(ix) 529
The prime factorisation of 529 is shown below:

Therefore, the prime factorisation of 529 = 23 × 23.
By pairing the prime factors we get,
529 = 23 × 23 = 232 = (23)2
So, √529 = 23.
Summary: Using the prime factorisation method we get the square root of 529 = 23.
(x) 8100
The prime factorisation of 8100 is shown below:

Therefore, the prime factorisation of 8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
By pairing the prime factors we get,
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 = 22 × 32 × 32 × 52 = (2 × 3 × 3 × 5)2
So, √8100 = 2 × 3 × 3 × 5 = 90.
Summary: Using the prime factorisation method we get the square root of 8100 = 90.
5. For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252 (ii) 180 (iii) 1008 (iv) 2028
(v) 1458 (vi) 768
Answers:
(i) 252
The prime factorisation of 252 is shown below:
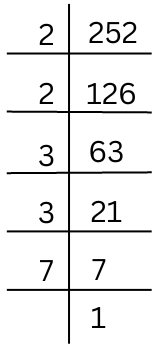
Therefore, the prime factorisation of 252 = 2 × 2 × 3 × 3 × 7.
By pairing the prime factors we get,
252 = 2 × 2 × 3 × 3 × 7
The prime factor 7 has no pair, so we multiply the number by 7 to get a perfect square number.
Therefore, 252 × 7 = 2 × 2 × 3 × 3 × 7 × 7.
Now each prime factor is a pair and the number = 252 × 7 = 1764.
√1764 = 2 × 3 × 7 = 42.
Summary: Therefore, the smallest whole number by which 252 should be multiplied so as to get a perfect square number is 7. The square root of the square number 1764 is 42.
(ii) 180
The prime factorisation of 180 is shown below:
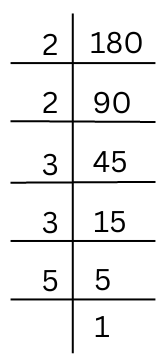
Therefore, the prime factorisation of 180 = 2 × 2 × 3 × 3 × 5.
By pairing the prime factors we get,
180 = 2 × 2 × 3 × 3 × 5
The prime factor 5 has no pair, so we multiply the number by 5 to get a perfect square number.
Therefore, 180 × 5 = 2 × 2 × 3 × 3 × 5 × 5.
Now each prime factor is a pair and the number = 180 × 5 = 900.
√900 = 2 × 3 × 5 = 30.
Summary: Therefore, the smallest whole number by which 180 should be multiplied so as to get a perfect square number is 5. The square root of the square number 900 is 30.
(iii) 1008
The prime factorisation of 1008 is shown below:
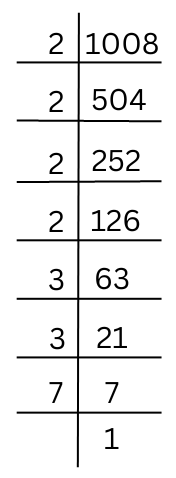
Therefore, the prime factorisation of 1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7.
By pairing the prime factors we get,
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
The prime factor 7 has no pair, so we multiply the number by 7 to get a perfect square number.
Therefore, 1008 × 7 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7.
Now each prime factor is a pair and the number 1008 × 7 = 7056.
√7056 = 2 × 2 × 3 × 7 = 84.
Summary: Therefore, the smallest whole number by which 1008 should be multiplied so as to get a perfect square number is 7. The square root of the square number 7056 is 84.
(iv) 2028
The prime factorisation of 2028 is shown below:

Therefore, the prime factorisation of 2028 = 2 × 2 × 3 × 13 × 13.
By pairing the prime factors we get,
2028 = 2 × 2 × 13 × 13 × 3
The prime factor 3 has no pair, so we multiply the number by 3 to get a perfect square number.
Therefore, 2028 × 3 = 2 × 2 × 13 × 13 × 3 × 3.
Now each prime factor is a pair and the number 2028 × 3 = 6084.
√6084 = 2 × 13 × 3 = 78.
Summary: Therefore, the smallest whole number by which 2028 should be multiplied so as to get a perfect square number is 3. The square root of the square number 6084 is 78.
(v) 1458
Answer:
The prime factorisation of 1458 is shown below:
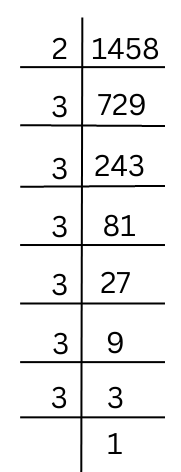
Therefore, the prime factorisation of 1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3.
By pairing the prime factors we get,
1458 = 3 × 3 × 3 × 3 × 3 × 3 × 2
The prime factor 2 has no pair, so we multiply the number by 2 to get a perfect square number.
Therefore, 1458 × 2 = 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2.
Now each prime factor is a pair and the number 1458 × 2 = 2916.
√2916 = 3 × 3 × 3 × 2 = 54.
Summary: Therefore, the smallest whole number by which 1458 should be multiplied so as to get a perfect square number is 2. The square root of the square number 2916 is 54.
(vi) 768
The prime factorisation of 768 is shown below:

Therefore, the prime factorisation of 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3.
By pairing the prime factors we get,
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
The prime factor 3 has no pair, so we multiply the number by 3 to get a perfect square number.
Therefore, 768 × 3 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3.
Now each prime factor is a pair and the number 768 × 3 = 2304.
√2304 = 2 × 2 × 2 × 2 × 3 = 48.
Summary: Therefore, the smallest whole number by which 768 should be multiplied so as to get a perfect square number is 3. The square root of the square number 2304 is 48.
6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252 (ii) 2925 (iii) 396 (iv) 2645
(v) 2800 (vi) 1620
Answers:
(i) 252
The prime factorisation of 252 is shown below:
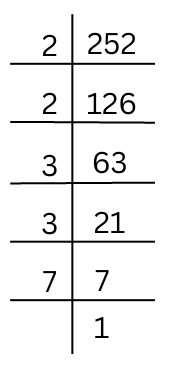
Therefore, the prime factorisation of 252 = 2 × 2 × 3 × 3 × 7.
By pairing the prime factors we get,
252 = 2 × 2 × 3 × 3 × 7
The prime factor 7 has no pair, so we divide the number by 7 to get a perfect square number.
Therefore, 252 ÷ 7 = 36 = 2 × 2 × 3 × 3 which is a perfect square. Therefore, the required smallest number is 7.
√36 = 2 × 3 = 6.
Summary: Therefore, the smallest whole number by which 252 should be divided so as to get a perfect square number is 7. The square root of the square number 36 is 6.
(ii) 2925
The prime factorisation of 2925 is shown below:
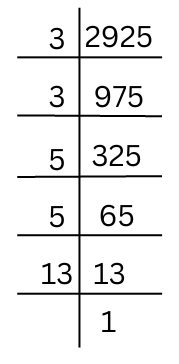
Therefore, the prime factorisation of 2925 = 3 × 3 × 5 × 5 × 13.
By pairing the prime factors we get,
2925 = 3 × 3 × 5 × 5 × 13
The prime factor 13 has no pair, so we divide the number by 13 to get a perfect square number.
Therefore, 2925 ÷ 13 = 225 = 3 × 3 × 5 × 5 which is a perfect square. Therefore, the required smallest number is 13.
√225 = 3 × 5 = 15.
Summary: Therefore, the smallest whole number by which 2925 should be divided so as to get a perfect square number is 13. The square root of the square number 225 is 15.
(iii) 396
The prime factorisation of 396 is shown below:

Therefore, the prime factorisation of 396 = 2 × 2 × 3 × 3 × 11.
By pairing the prime factors we get,
396 = 2 × 2 × 3 × 3 × 11
The prime factor 11 has no pair, so we divide the number by 11 to get a perfect square number.
Therefore, 396 ÷ 11 = 36 = 2 × 2 × 3 × 3 which is a perfect square. Therefore, the required smallest number is 11.
√36 = 2 × 3 = 6.
Summary: Therefore, the smallest whole number by which 396 should be divided so as to get a perfect square number is 11. The square root of the square number 36 is 6.
(iv) 2645
The prime factorisation of 2645 is shown below:

Therefore, the prime factorisation of 2645 = 5 × 23 × 23.
By pairing the prime factors we get,
2645 = 23 × 23 × 5
The prime factor 5 has no pair, so we divide the number by 5 to get a perfect square number.
Therefore, 2645 ÷ 5 = 529 = 23 × 23 which is a perfect square. Therefore, the required smallest number is 5.
√529 = 23.
Summary: Therefore, the smallest whole number by which 2645 should be divided so as to get a perfect square number is 5. The square root of the square number 529 is 23.
(v) 2800
The prime factorisation of 2800 is shown below:

Therefore, the prime factorisation of 2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7.
By pairing the prime factors we get,
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7.
The prime factor 7 has no pair, so we divide the number by 7 to get a perfect square number.
Therefore, 2800 ÷ 7 = 400 = 2 × 2 × 2 × 2 × 5 × 5 which is a perfect square. Therefore, the required smallest number is 7.
√400 = 2 × 2 × 5 = 20.
Summary: Therefore, the smallest whole number by which 2800 should be divided so as to get a perfect square number is 7. The square root of the square number 400 is 20.
(vi) 1620
The prime factorisation of 1620 is shown below:

Therefore, the prime factorisation of 1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5.
By pairing the prime factors we get,
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5.
The prime factor 5 has no pair, so we divide the number by 5 to get a perfect square number.
Therefore, 1620 ÷ 5 = 324 = 2 × 2 × 3 × 3 × 3 × 3 which is a perfect square. Therefore, the required smallest number is 5.
√324 = 2 × 3 × 3 = 18.
Summary: Therefore, the smallest whole number by which 1620 should be divided so as to get a perfect square number is 5. The square root of the square number 324 is 18.
7. The students of Class VIII of a school donated ₹ 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Answer:
Let the number of students in the class be x.
The amount of money each student donated also = x.
So the total amount of money donated = (x) × (x) = ₹ x2.
Therefore, x2 = 2401.
The prime factorisation of 2401 is done as follows:
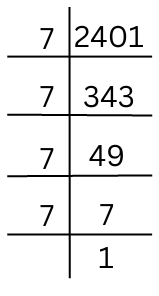
2401 = 7 × 7 × 7 × 7 = 7 × 7 × 7 × 7.
x2 = 2401 = 7 × 7 × 7 × 7.
or, x = √2401 = 7 × 7 = 49.
Summary: The number of students in the class = 49.
8. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Answer:
Let the number of rows be x. So, the number of plants in each row also = x.
Hence, the total number of plants = x2 = 2025.
The prime factorisation of 2025 is done:
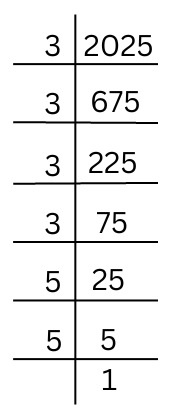
2025 = 3 × 3 × 3 × 3 × 5 × 5
x2 = 2025 = 3 × 3 × 3 × 3 × 5 × 5
or x = √2025 = 3 × 3 × 5 = 45.
Summary: The number of rows and the number of plants in each row both = 45.
9. Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Answer: The least number which is divisible by each of 4, 9 and 10 is the LCM:

LCM = 2 × 2 × 9 × 5 = 180.
Now 180 = 2 × 2 × 9 × 5 = 2 × 2 × 3 × 3 × 5 = 2 × 2 × 3 × 3 × 5.
Since 5 is unpaired we multiply the LCM by 5 to make it a perfect square.
Therefore, required smallest square number that is divisible by 4, 9 and 10= 180 × 5 = 900.
10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Answer: The least number which is divisible by each of 8, 15 and 20is the LCM:

LCM = 2 × 2 × 5 × 2 × 3 = 120.
Now 120 = 2 × 2 × 2 × 3 × 5 = 2 × 2 × 2 × 3 × 5.
Since 2, 3, 5 are unpaired we multiply the LCM by (2 × 3 × 5) to make it a perfect square.
Therefore, required smallest square number that is divisible by 8, 15 and 20 = 120 × 2 × 3 × 5 = 3600.
Solutions to Exercise 5.4 (Page No 69) of NCERT Class 8 Mathematics Chapter 5 Squares and Square Roots:
1. Find the square root of each of the following numbers by Division method.
(i) 2304 (ii) 4489 (iii) 3481 (iv) 529
(v) 3249 (vi) 1369 (vii) 5776 (viii) 7921
(ix) 576 (x) 1024 (xi) 3136 (xii) 900
Answers:
(i) 2304
The square root of 2304 can be calculated by division method:

Therefore, √2304 = 48.
(ii) 4489
The square root of 4489 can be calculated by division method:

Therefore, √4489 = 67.
(iii) 3481
The square root of 3481 can be calculated by division method:

Therefore, √3481 = 59.
(iv) 529
The square root of 529 can be calculated by division method:

Therefore, √529 = 23.
(v) 3249
The square root of 3249 can be calculated by division method:

Therefore, √3249 = 57.
(vi) 1369
The square root of 1369 can be calculated by division method:
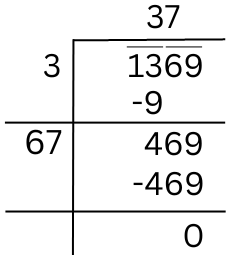
Therefore, √1369 = 37.
(vii) 5776
The square root of 5776 can be calculated by division method:

Therefore, √5776 = 76.
(viii) 7921
The square root of 7921 can be calculated by division method:
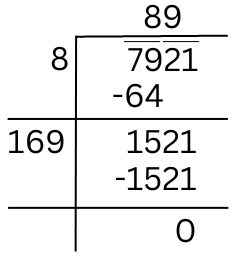
Therefore, √7921 = 89.
(ix) 576
The square root of 576 can be calculated by division method:

Therefore, √576 = 24.
(x) 1024
The square root of 1024 can be calculated by division method:

Therefore, √1024 = 32.
(xi) 3136
The square root of 3136 can be calculated by division method:

Therefore, √3136 = 56.
(xii) 900
The square root of 900 can be calculated by division method:

Therefore, √900 = 30.
2. Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64 (ii) 144 (iii) 4489 (iv) 27225 (v) 390625
Answers:
(i) 64
If a perfect square is of n digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd.
64 has 2 digits which is even and hence the number of digits in its square root 2/2 = 1.
(ii) 144
If a perfect square is of n digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd.
144 has 3 digits which is odd and hence the number of digits in its square root (3 + 1)/2 = 4/2 = 2.
(iii) 4489
If a perfect square is of n digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd.
4489 has 4 digits which is even and hence the number of digits in its square root 4/2 = 2.
(iv) 27225
If a perfect square is of n digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd.
27225 has 5 digits which is odd and hence the number of digits in its square root (5 + 1)/2 = 6/2 = 3.
(v) 390625
390625 has 6 digits which is even and hence the number of digits in its square root 6/2 = 3.
Summary: (i) The number of digits in the square root of 64 is 1, (ii) number of digits in square root of 144 is 2, (iii) number of digits in square root of 4489 is 2, (iv) number of digits in square root of 27225 is 3, number of digits in square roots of 390625 is 3.
3. Find the square root of the following decimal numbers.
(i) 2.56 (ii) 7.29 (iii) 51.84 (iv) 42.25
(v) 31.36
Answers:
(i) 2.56
The square root of 2.56 can be found using division method:
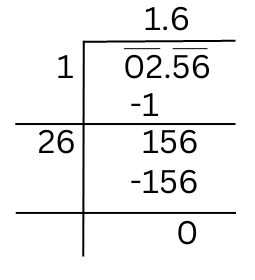
Therefore, √2.56 = 1.6
(ii) 7.29
The square root of 7.29 can be found using division method:

Therefore, √7.29 = 2.7
(iii) 51.84
The square root of 51.84 can be found using division method:
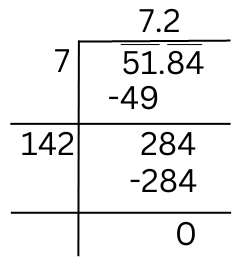
Therefore, √51.84 = 7.2
(iv) 42.25
The square root of 42.25 can be found using division method:

Therefore, √42.25 = 6.5
(v) 31.36
The square root of 31.36 can be found using division method:
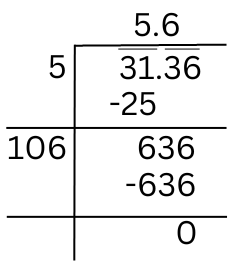
Therefore, √31.36 = 5.6
Summary: Using division method the square roots can be found. The square root of (i) 2.56 is 1.6, square root of (ii) 7.29 is 2.7, square root of (iii) 51.84 is 7.2, (iv) square root of 42.25 is 6.5, square root of 31.36 is 5.6.
4. Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402 (ii) 1989 (iii) 3250 (iv) 825 (v) 4000
Answers:
(i) 402
When we try to find the square root of 402 by long division method, we get the remainder 2.
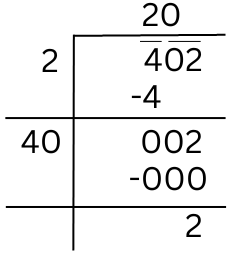
It shows that 202 is less than 402 by 2. This means if we subtract 2 from the number we get a perfect square. Therefore, the required perfect square = 402 – 2 = 400. Also since 400 = 202, √400 = 20.
(ii) 1989
When we try to find the square root of 1989 by long division method, we get the remainder 53.

It shows that 442 is less than 1989 by 53. This means if we subtract 53 from the number we get a perfect square. Therefore, the required perfect square = 1989 – 53 = 1936. Also since 1936 = 442, √1936 = 44.
(iii) 3250
When we try to find the square root of 1989 by long division method, we get the remainder 1.

It shows that 572 is less than 3250 by 1. This means if we subtract 1 from the number we get a perfect square. Therefore, the required perfect square = 3250 – 1 = 3249. Also since 3249 = 572, √3249 = 57.
(iv) 825
When we try to find the square root of 825 by long division method, we get the remainder 41.
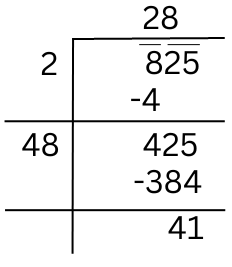
It shows that 282 is less than 825 by 41. This means if we subtract 41 from the number we get a perfect square. Therefore, the required perfect square = 825 – 41 = 784. Also since 784 = 282, √784 = 28.
(v) 4000
When we try to find the square root of 4000 by long division method, we get the remainder 31.
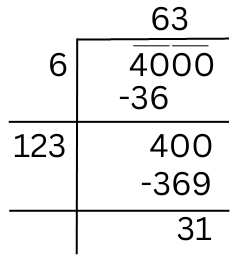
It shows that 632 is less than 4000 by 31. This means if we subtract 31 from the number we get a perfect square. Therefore, the required perfect square = 4000 – 31 = 3969. Also since 3969 = 632, √3969 = 63.
5. Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525 (ii) 1750 (iii) 252 (iv) 1825 (v) 6412
Answers:
(i) 525
We try to find √525 by long division method.

The remainder is 41. This shows that 222 < 525. Next perfect square number is 232 = 529.
Hence the number to be added to 525 to get a perfect square is (529 – 525) = 4.
Square root of 529 = √529 = 23.
(ii) 1750
We try to find √1750 by long division method.
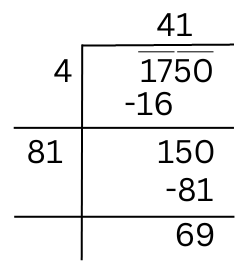
The remainder is 69. This shows that 412 < 1750. So we take the next perfect square number which is 422 = 1764.
Hence the number to be added to 1750 to get a perfect square is (1764 – 1750) = 14.
Square root of 1764 = √1764 = 42.
(iii) 252
We try to find √252 by long division method.
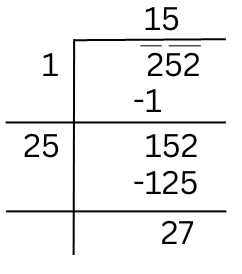
The quotient is 15 and remainder is 27. This shows that 152 < 252. So we take the next perfect square number which is 162 = 256.
Hence the number to be added to 252 to get a perfect square is (256 – 252) = 4.
Square root of 256 = √256 = 16.
(iv) 1825
We try to find √1825 by long division method.
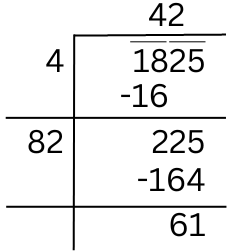
The quotient is 42 and remainder is 61. This shows that 422 < 1825. So we take the next perfect square number which is 432 = 1849.
Hence the number to be added to 1825 to get a perfect square is (1849 – 1825) = 24.
Square root of 1849 = √1849 = 43.
(v) 6412
We try to find √6412 by long division method.

The quotient is 80 and remainder is 12. This shows that 802 < 6400. So we take the next perfect square number which is 812 = 6561.
Hence the number to be added to 6412 to get a perfect square is (6561 – 6412) = 49.
Square root of 6561 = √6561 = 81.
Summary: The least number which must be added to (i) 525, (ii) 1750, (iii) 252, (iv) 1825 and (v) 6412 get a perfect square is (i) 4, (ii) 14, (iii) 4, (iv) 24 and (v) 49 respectively. The square roots of the perfects squares are: (i) 23, (ii) 42, (iii) 16, (iv) 43 and (v) 81 respectively.
6. Find the length of the side of a square whose area is 441 m2.
Answer:
Area of the square = (Length of side)2 = 441 m2.
Therefore, length of √441 = 21 m.
7. In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC (b) If AC = 13 cm, BC = 5 cm, find AB
Answers:
(a) If AB = 6 cm, BC = 8 cm, find AC
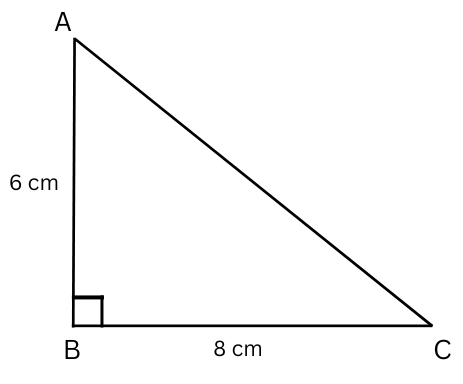
Given, AB = 6 cm, BC = 8 cm.
Using Pythagoras theorem, AC2 = AB2 + BC2.
or, AC2 = 62 + 82 = 36 + 64 = 100.
or, AC = √100 = 10 cm.
(b) If AC = 13 cm, BC = 5 cm, find AB
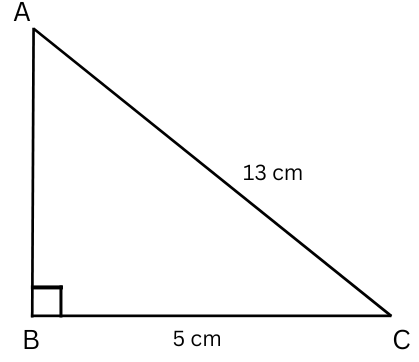
Given: AC = 13 cm, BC = 5 cm.
Using Pythagoras theorem, AC2 = AB2 + BC2.
or, 132 = AB2 + 52
or, AB2 = 132 – 52
or, AB2 = 169 – 25
or, AB2 = 144
or, AB = √144 = 12 cm.
8. A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Answer: Let the number of rows = number of columns = x.
Therefore, total number of plants = (x) × (x) = x2.
Let us try to find the square root of 1000.
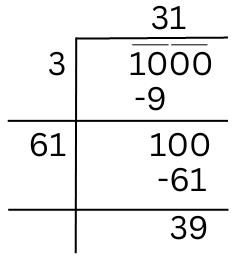
The quotient is 31 and the remainder is 39. This shows that 312 < 1000. So we take the next perfect square number which is 322 = 1024.
Hence the minimum number of more plants he needs = (1024 – 1000) = 24.
9. There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement.
Answer:
Let the number of rows = number of columns = x.
Therefore, the total number of children = (x) × (x) = x2.
Let us try to find the square root of 500.
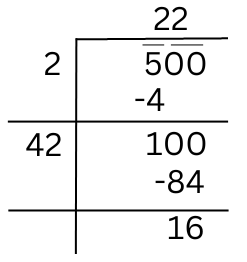
The remainder is 16.
Hence the number of children who would be left out in this arrangement = 16.
Extra Questions to Complement Solutions to NCERT Class 8 Mathematics Chapter 5 Squares and Square Roots:
Very Short Answer Type Questions:
1. Is the digit in the unit’s place of the square of 68 and 84 even or odd?
Answer:
The digit in the unit’s place of the square of all even numbers is even. 68 and 84 are even numbers. So, 682 and 842 both have even numbers in the unit’s place.
2. What is the digit in the unit’s place of the square of 89?
Answer:
If a number has 9 in the unit’s place then its square ends in 1. Therefore, the digit in the unit’s place of the square of 89 = 1. You can verify by multiplying the unit’s digit with itself and taking the rightmost digit (9 × 9 = 81).
3. Tell just by observation if 838 can be a square number.
Answer:
We know that numbers ending with 2, 3, 7 or 8 at the unit’s place cannot be perfect squares. Since 838 ends with the digit 8 it cannot be a perfect square number.
4. Tell just by observation if 900000 is a perfect square number.
Answer:
Perfect square numbers have an even number of zeros at the end. Since 900000 has 5 zeros it cannot be a perfect square number.
5. I am a two-digit number and end with 6. Two successive integral square roots can be obtained using me. What number am I?
Answer:
The number is 16. The first square root = √16 = 4. The second square root = √4 = 2.
6. Can you express 1 + 3 + 7 + 9 + 11 + 13 + 15 as a perfect square?
Answer:
We know that the sum of first n natural numbers is n2. Therefore, a perfect square number can be expressed as the sum of successive odd natural numbers starting with 1.
We observe,
1 + 3 + 7 + 9 + 11 + 13 + 15 is missing the digit 5. Hence, the sum cannot be a perfect square number.
The sum = 59 which is not a perfect square number. Hence, verified.
7. What is the least number by which 24 should be multiplied so that the resulting number is a perfect square?
Answer:
Prime factorisation of 24 = 2 × 2 × 2 × 3. Here 2 and 3 is unpaired. Hence if we multiply the number by 2 × 3 it will become a perfect square.
24 × 2 × 3 = 2 × 2 × 2 × 2 × 3 × 3.
Therefore the least number by which 24 should be multiplied so that the resulting number is a perfect square = 2 × 3 = 6.
8. Can you form a right-angled triangle with sides 3 cm, 5 cm, and 6 cm?
Answer:
Let the longest side or hypotenuse = 6 cm. 62 is not equal to (32 + 52) and so 3, 5 and 6 do not form a Pythagorean triplet. Hence, a right-angled triangle cannot be formed.
9. Which is greater: 1/10 or 1/√10 ?
Answer:
We know that 10 > √10. Therefore, since the denominator of 1/√10 is smaller, the number 1/√10 is larger.
10. Name three methods of finding the square root of a number.
Answer:
Three methods of finding the square root of a number are repeated subtraction, prime factorisation and division method.
Multiple Choice Questions (MCQ):
1. Which of the following numbers can have square roots?
(a) Fractions
(b) Integers
(c) Decimals
(d) All
Answer: Correct answer: (d) All. All non-negative numbers can have square roots.
2. Which of the following numbers will have the digit 6 at unit’s place.
(a) 192
(b) 242
(c) 482
(d) 892
Answer: Correct answer: (b) 242. Since 24 has the digit 4 in the unit’s place, 242 will have the digit 6 at unit place.
3. Which of the following gives you the square root (s) of 49?
(a) 7
(b) – 7
(c) 7 and – 7
(d) None of the above
Answer: Correct answer: (c) 7 and – 7.
4. The next two numbers in the number pattern 1, 4, 9, 16, 25 … are (NCERT Exemplar)
(a) 35, 48
(b) 36, 49
(c) 36, 48
(d) 35,49
Answer: Correct answer: (b) 36, 49.
1, 4, 9, 16, 25 … can be written as 12, 22, 32, 42, 52… Therefore the next two terms are 62 and 72 or 36 and 49 respectively.
5. Find the value of (√36 × √16)/√9 :
(a) 8
(b) 8/3
(c) 9
(d) 8/9
Answer: Correct answer: (a) 8.
(√36 × √16)/√9 = (6 × 4)/3 = 8.
Short and Long Answer Type Questions:
1. We know for any natural number m > 1, we have (2m)2 + (m2 – 1)2 = (m2 + 1)2. 2m, m2 – 1 and m2 + 1 form a Pythagorean triplet. Check to see if all Pythagorean triplets can be obtained using this form.
Answer: We take the Pythagorean triplet 5, 12 and 13.
We can clearly see that:
If 2m = 5, m = 5/2 which is not an integer.
So the above is not possible.
If 2m = 12, m = 6.
m2 – 1 = 12 or m2 = 13 or m = √13 which is not an integer.
So the above is not possible.
If 2m = 13, m = 13/2 which is not an integer.
So the above is also not possible.
Therefore, the Pythagorean triplet 5, 12 and 13 cannot be obtained using the form (2m)2 + (m2 – 1)2 = (m2 + 1)2. Hence all Pythagorean triplets cannot be obtained using this form.
2. How many numbers lie between the squares of the two consecutive square numbers 2k and 2k + 1?
Answer: We know that 2n non perfect square numbers lie between the squares of the numbers n and (n + 1).
Here n = 2k.
Therefore, 2n = 2 × 2k = 4k Hence number of non-perfect square numbers that lie between the squares of 2k and 2k + 1 = 4k.
3. Calculate the sum of 5 + 7 + 9 + 11 + 13 + 15 using the formulae that sum of first n natural numbers is n2.
Answer: We can write:
5 + 7 + 9 + 11 + 13 + 15 = (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15) – (1 + 3)
Since sum of first n natural numbers is n2,
(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15) = 82 = 64.
Therefore,
5 + 7 + 9 + 11 + 13 + 15
= (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15) – (1 + 3)
= 64 – 4 = 60 (Answer)
4. Prove that:
(i) 12 × 14 = 132 – 1 (ii) 17 × 19 = 182 – 1
Answers:
(i) 12 × 14
= (13 – 1) × (13 + 1)
= 132 + 13 – 13 – 1
= 132 – 1 (Hence proved)
(ii) 17 × 19
= (18 – 1) × (18 + 1)
= 182 + 18 – 18 – 1 = 182 – 1 (Hence proved)
5. Find the square roots of the following numbers without actual multiplication:
(i) 28 (ii) 49 (ii) 61
Answers:
(i) 28
282 = (20 + 8)2
= 20(20 + 8) +8(20 + 8)
= 202 + 20 × 8 + 8 × 20 + 82
= 400 + 160 + 160 + 64
= 784 (Answer)
(ii) 49
492 = (40 + 9)2
= 40(40 + 9) + 9(40 + 9)
= 402 + 40 × 9 + 9 × 40 + 9 × 9
= 1600 + 360 + 360 + 81
= 2401 (Answer)
(iii) 61
612 = (60 + 1)2
= 60(60 + 1) + 1(60 + 1)
= 602 + 60 + 60 + 1
= 3600 + 60 + 60 + 1
= 3721 (Answer)
6. Look at the two squares in the given figure. What is the width of the region between the two squares?

Answer: Let length of outer square be l1.
Area of outer square = l12 = 81.
or, l1 = √81 = 9 m.
Let length of outer square be l2.
Area of inner square = l22 = 64.
or, l2 = √64 = 8 m.
Let the width of the region between the two squares be x.

From the figure we can see that x + l2 + x = l1.
2x = l1 – l2 = 9 – 8 = 1 m.
or, x = 1/2
Therefore, the width of the region between the two squares is 1/2 m.
7. Is it possible to form a square with equal rows and columns by using all of 500 students?
Answer: Let the number of students in each row = number of students in each column = x.
Then total number of students = (x) × (x) = x2.
If a square is to be formed then x2 will have to be equal to 500.
Let us try to find the square root of 500.

Thus, we can see that 500 is not a perfect square. If we form equal rows and columns of 22 students each, we will have 16 students (remainder of quotient) left over.
Hence, it is not possible to form a square with equal rows and columns by using all of 500 students.
8. A factory has 2400 identical products to package. The manager wants to pack them in a square-shaped container, with the same number of rows and columns. Find the minimum number of extra products needed to fill the container.
Answer: Let the number of rows = number of columns = x.
Then total number of students = (x) × (x) = x2.
If a square is to be formed then x2 will have to be equal to 2400.
Let us try to find the square root of 2400.

The quotient is 48 and remainder is 96. This shows that 482 < 2400. So, we take the next perfect square number which is 492 = 2401.
Hence, in order to achieve the right arrangement the minimum number of extra products need = (2401 – 2400) = 1.
9. Estimate the square root of √350 to the nearest whole number.
Answer:
We know that, 225 < 350 < 400 and √225 = 15 and √400 = 20.
So, 15 < √350 < 20.
But still we are not very close to the square number.
We know that 182 = 324 and 192 = 361.
Therefore, 18 < √350 < 19 and 361 is much closer to 350 than 324.
So, √350 is approximately 19.
Fill in the Blanks:
(a) Square root of a number can be found by repeated _________ of successive odd natural numbers starting from 1.
(b) The number of digits in the square root of a 5-digit or 6-digit perfect square is _________.
(c) If you find the square root of a perfect square number by division method, the remainder will be _________.
(d) √80 is _________ than √70.
(e) The number of integral square roots of a perfect square number is _________.
Answers:
(a) Square root of a number can be found by repeated subtraction of successive odd natural numbers starting from 1.
(b) The number of digits in the square root of a 5-digit or 6-digit perfect square number is 3.
(c) If you find the square root of a perfect square number by division method, the remainder will be 0.
(d) √80 is greater than √70.
(e) The number of integral square roots of a perfect square number is two.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 8 Mathematics Chapter 5 Squares and Square Roots:
These solutions and extra material have been designed by an expert team of Indian and foreign-educated teachers, engineers and scientists. All the different problem-solving techniques are shown clearly in the exercise solutions as well as the extra material. We advise you practise them well. They will help you develop the skills you need to solve unknown problems on your own.
You can download the free PDFs of the solutions anytime! Get the latest material and other resources delivered straight to your inbox by subscribing to our email list. Happy preparing!
The following topics are covered:
5.1 – Introduction
5.2 – Properties of Square Numbers
5.3 – Some More Interesting Patterns
5.4 – Finding the Square of a Number
5.5 – Square Roots
5.6 – Square Roots of Decimals
Here are the number of problems for the chapter:
Exercise 6.1 – 9 Problems
Exercise 6.2 – 2 Problems
Exercise 6.3 – 10 Problems
Exercise 6.4 – 9 Problems
Of course! You can download the PDF version of educationroundtheworld.com’s NCERT Solutions for Class 8 Mathematics Chapter 5 Squares and Square Roots anytime you please! The solutions including the self-designed extra questions are included in the PDF version! Please look towards the top of the page to find the download button!
Carefully study the properties and patterns related to square numbers. Then look at the problems we have designed which makes use of those techniques. Secondly, practise the various methods of obtaining and estimating square roots until they are like second nature to you. Lastly, practise the word problems in the book and also the ones we have included in the extra material. Make sure to solve them on your own while looking at our solutions. Good luck!
If you need extra training, we can be your best guide! Our expert teachers will clear all your doubts, prepare you for your exams and provide expert counselling. Feel free to reach out to us anytime and let us help you out!
No worries! We provide you with a dedicated teacher cum mentor, who will prepare you for exams as well as counsel you about your future. Sounds good? Feel free to reach out to us anytime!
We provide expert one-on-one coaching and mentoring to you depending on your convenience and needs – have it completely your way! Book an appointment now!


