Solutions to NCERT Class 8 Mathematics Chapter 6 Cubes and Cube Roots

Hello students! You learnt about squares and square roots in Chapter 5, now it’s time for Chapter 6 Cubes and Cube Roots. As usual, our solutions and extra material are an excellent place to begin your study. Find the material below and we advise that you practise the problems on your own as well. This will help you understand and retain the material better.

Solutions to Exercise 6.1 (Page No 76) of NCERT Class 8 Mathematics Chapter 6 Cubes and Cube Roots:

1. Which of the following numbers are not perfect cubes?

Answers:

A number is a perfect cube if all its like prime factors can be grouped into triplets.

(i) 216

The prime factorisation of 216 is done.

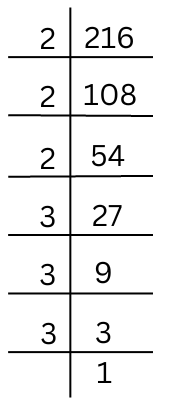
216 = 2 × 2 × 2 × 3 × 3 × 3 (Grouping like factors into triplets)

Each factor appears 3 times.

216 = 2³ × 3³ = (2 × 3)³ = 6³ which is a perfect cube. Thus 216 is a perfect cube.

(ii) 128

The prime factorisation of 128 is done.

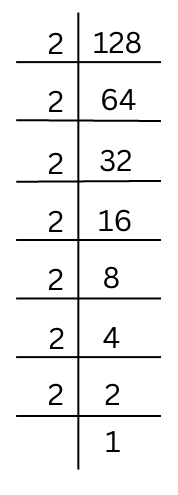
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2.

When we try to group like factors into triplets there is one 2 left.

So, 128 is not a perfect cube.

(iii) 1000

The prime factorisation of 1000 is done.

1000 = 2 × 2 × 2 × 5 × 5 × 5 (Grouping like factors into triplets)

Each factor appears 3 times.

1000 = 2³ × 5³ = (2 × 5)³ = 10³ which is a perfect cube. Thus 1000 is a perfect cube.

(iv) 100

The prime factorisation of 100 is done.

100 = 2 × 2 × 5 × 5

So, 100 cannot be grouped into triplets of like factors. Hence, 100 is not a perfect cube.

(v) 46656

The prime factorisation of 46656 is done.

46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 (Grouping like factors into triplets)

Each factor appears in groups of three.

46656 = 2³ × 2³ × 3³ × 3³ = (2 × 2 × 3 × 3)³ = 36³ which is a perfect cube. Thus 46656 is a perfect cube.

Summary: A number is a perfect cube if all its like prime factors can be grouped into triplets. (i) 216 is a perfect cube. (ii) 128 is not a perfect cube. (iii) 1000 is a perfect cube. (iv) 100 is not a perfect cube. (v) 46656 is a perfect cube.

2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.

Answers:

(i) 243

The prime factorisation of 243 is done.

243 = 3 × 3 × 3 × 3 × 3 (Grouping like factors into triplets)

We must convert the isolated (3 × 3) into a triplet by multiplying by 3.

243 × 3 = 3 × 3 × 3 × 3 × 3 × 3 = 729 which is a perfect cube.

Hence, the smallest number by which 243 should be multiplied to get a perfect cube is 3.

(ii) 256

The prime factorisation of 256 is done.

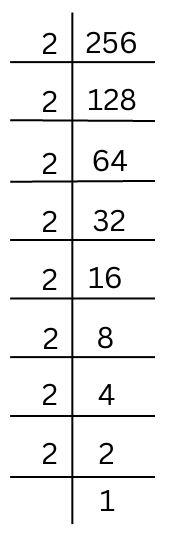
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2  (Grouping like factors into triplets)

We must convert the isolated (2 × 2) into a triplet by multiplying by 2.

256 × 2 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512 which is a perfect cube.

Hence, the smallest number by which 256 should be multiplied to get a perfect cube is 2.

(iii) 72

The prime factorisation of 72 is done.

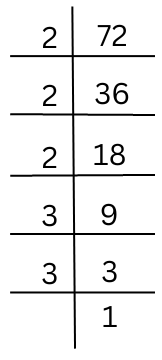
72 = 2 × 2 × 2 × 3 × 3 (Grouping like factors into triplets)

We must convert the isolated (3 × 3) into a triplet by multiplying by 3.

72 × 3 = 2 × 2 × 2 × 3 × 3 × 3 = 216 which is a perfect cube.

Hence, the smallest number by which 216 should be multiplied to get a perfect cube is 3.

(iv) 675

The prime factorisation of 675 is done.

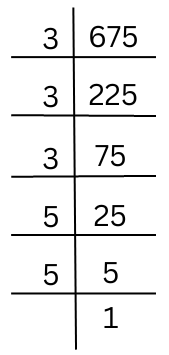
675 = 3 × 3 × 3 × 5 × 5 (Grouping like factors into triplets)

We must convert the isolated (5 × 5) into a triplet by multiplying by 5.

675 × 5 = 3 × 3 × 3 × 5 × 5 × 5 = 3375 which is a perfect cube.

Hence, the smallest number by which 675 should be multiplied to get a perfect cube is 5.

(v) 100

The prime factorisation of 100 is done.

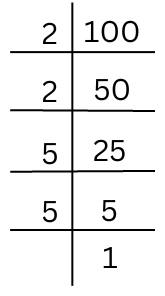
100 = 2 × 2 × 5 × 5

We must convert both (2 × 2) and (5 × 5) into triplets by multiplying by 2 and 5 respectively.

100 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5 = 1000 which is a perfect cube. Required number = 2 × 5 = 10.

Hence, the smallest number by which 100 should be multiplied to get a perfect cube is 10.

3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.

(i) 81

The prime factorisation of 81 is done.

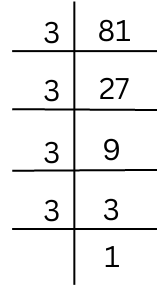
81 = 3 × 3 × 3 × 3

There is an isolated 3 that remains after grouping like factors into triplets.

Hence, we have to divide by 3 to obtain a perfect cube.

Hence, 81 ÷ 3 = 3 × 3 × 3 = 3³ which is a perfect cube.

Hence, the smallest number by which 81 should be divided to obtain a perfect cube is 3.

(ii) 128

The prime factorisation of 128 is done.

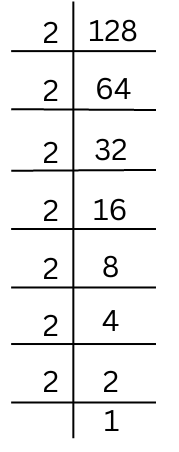
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2

There is an isolated 2 that remains after grouping like factors into triplets.

Hence, we have to divide by 2 to obtain a perfect cube.

Hence, 128 ÷ 2 = 2 × 2 × 2 × 2 × 2 × 2 which is a perfect cube.

Hence, the smallest number by which 128 should be divided to obtain a perfect cube is 2.

(iii) 135

The prime factorisation of 135 is done.

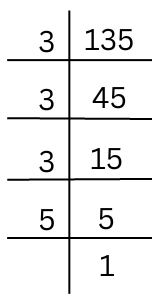
135 = 3 × 3 × 3 × 5

There is an isolated 5 that remains after grouping like factors into triplets.

Hence, we have to divide by 5 to obtain a perfect cube.

Hence, 135 ÷ 5 = 3 × 3 × 3 which is a perfect cube.

Hence, the smallest number by which 135 should be divided to obtain a perfect cube is 5.

(iv) 192

The prime factorisation of 192 is done.

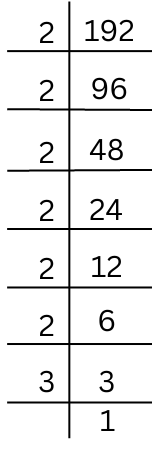
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3

There is an isolated 3 that remains after grouping like factors into triplets.

Hence, we have to divide by 3 to obtain a perfect cube.

Hence, 192 ÷ 3 = 2 × 2 × 2 × 2 × 2 × 2 which is a perfect cube.

Hence, the smallest number by which 192 should be divided to obtain a perfect cube is 3.

(v) 704

The prime factorisation of 704 is done.

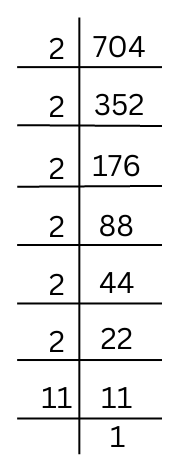
704 = 2 × 2 × 2 × 2 × 2 × 2 × 11

There is an isolated 11 that remains after grouping like factors into triplets.

Hence, we have to divide by 11 to obtain a perfect cube.

Hence, 704 ÷ 11 = 2 × 2 × 2 × 2 × 2 × 2 which is a perfect cube.

Hence, the smallest number by which 704 should be divided to obtain a perfect cube is 11.

4. Parikshit makes a cuboid of plasticine with sides 5 cm, 2 cm, and 5 cm. How many such cuboids will he need to form a cube?

Answer: The sides of the cuboid are 5 cm, 2 cm and 5 cm.

Volume of cuboid = 5 × 2 × 5 = 50.

The prime factorisation of 50 is done.

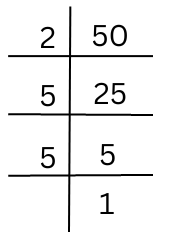
50 = 2 × 5 × 5

There are only one 2 and two 5’s in the prime factorisation.

Hence, we need to multiply by (2 × 2 × 5) = 20 to form a perfect cube.

Therefore, the number of such cuboids needed to form the cube = 20.

Solutions to Exercise 6.2 (Page No 77) of NCERT Class 8 Mathematics Chapter 6 Cubes and Cube Roots:

1. Find the cube root of each of the following numbers by the prime factorisation method.

(i) 64

Prime factorisation of 64 is done.

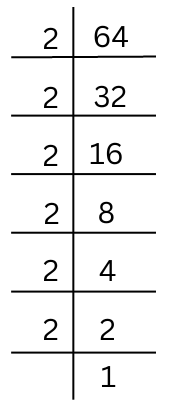
64 = 2 × 2 × 2 × 2 × 2 × 2 (Grouping like factors into triplets)

So, ∛64 = 2 × 2 = 4.

Hence, cube root of 64 is 4.

(ii) 512

Prime factorisation of 512 is done.

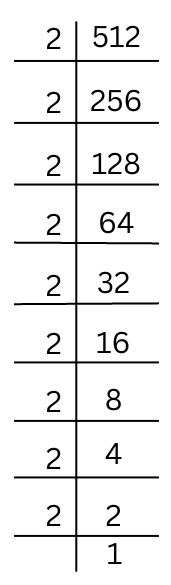
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 (Grouping like factors into triplets)

So, ∛512 = 2 × 2 × 2 = 8.

Hence, cube root of 512 is 8.

(iii) 10648

Prime factorisation of 10648 is done.

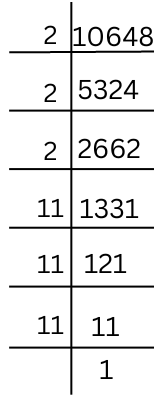
10648 = 2 × 2 × 2 × 11 × 11 × 11 (Grouping like factors into triplets)

So, ∛10648 = 2 × 11 = 22.

Hence, cube root of 10648 is 22.

(iv) 27000

Prime factorisation of 27000 is done.

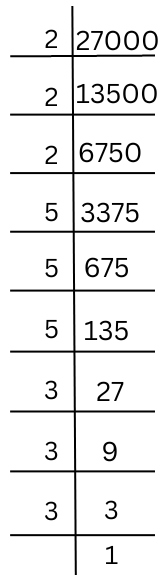
27000 = 2 × 2 × 2 × 5 × 5 × 5 × 3 × 3 × 3 (Grouping like factors into triplets)

So, ∛27000 = 2 × 5 × 3 = 30.

Hence, cube root of 27000 is 30.

(v) 15625

Prime factorisation of 15625 is done.

15625 = 5 × 5 × 5 × 5 × 5 × 5 (Grouping like factors into triplets)

So, ∛15625 = 5 × 5 = 25.

Hence, cube root of 15625 is 25.

(vi) 13824

Prime factorisation of 13824 is done.

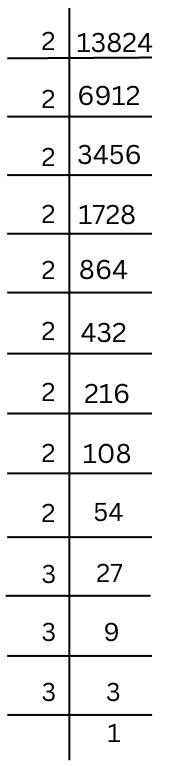
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 (Grouping like factors into triplets)

So, ∛13824 = 2 × 2 × 2 × 3 = 24.

Hence, cube root of 13824 is 24.

(vii) 110592

Prime factorisation of 110592 is done.

110592 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 (Grouping like factors into triplets)

So, ∛110592 = 2 × 2 × 2 × 2 × 3 = 48.

Hence, cube root of 110592 is 48.

(viii) 46656

Prime factorisation of 46656 is done.

46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 (Grouping like factors into triplets)

So, ∛46656 = 2 × 2 × 3 × 3 = 36.

Hence, cube root of 46656 is 36.

(ix) 175616

Prime factorisation of 175616 is done.

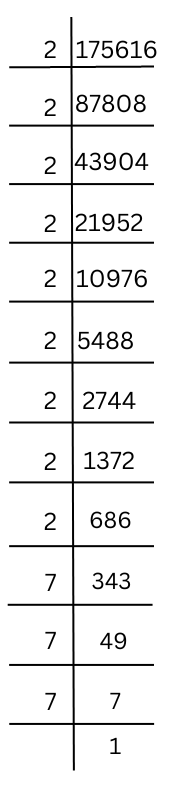
175616 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 × 7 (Grouping like factors into triplets)

So, ∛175616 = 2 × 2 × 2 × 7 = 56.

Hence, cube root of 175616 is 36.

(x) 91125

Prime factorisation of 91125 is done.

91125 = 3 × 3 × 3 × 3 × 3 × 3 × 5 × 5 × 5 (Grouping like factors into triplets)

So, ∛91125 = 3 × 3 × 5 = 45.

Hence, cube root of 91125 is 45.

2. State true or false.

(i) Cube of any odd number is even.

Answer: False. Cube of any odd number is odd.

(ii) A perfect cube does not end with two zeros.

Answer: True. A perfect cube ends with a minimum of three zeros.

(iii) If square of a number ends with 5, then its cube ends with 25.

Answer: False. For example for the number 15, 15² = 225 which ends with 5. However, 15³ = 3375 which ends with 75.

(iv) There is no perfect cube which ends with 8.

Answer: False. For example, the number 10648 ending with 8 is a perfect cube because ∛10648 = 22.

(v) The cube of a two-digit number may be a three-digit number.

Answer: False. Let us take the smallest two-digit number 10. We get 10³ = 1000 which has four digits. Therefore, the cubes of all two-digit numbers > 10 will have at least four digits.

(vi) The cube of a two-digit number may have seven or more digits.

Answer: False. Let us take the largest number two-digit99. We get 99³ = 970299 which has 6 digits. Therefore, a two digit number can never have seven or more digits.

(vii) The cube of a single-digit number may be a single-digit number.

Answer: True. Let us take the single digit number 2. Now, 2³ = 8 which has one digit. Hence, the above statement is True.

Important Questions from Previous NCERT Textbook:

Exercise 7.2 Page No: 116 (Old Textbook):

3. You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.

Answer:

(i) 1331

Step 1: We start making groups of three digits starting from the rightmost digit. Therefore, first group = 331 and second group is 1.

Step 2: The first group will give you the unit’s digit of the required root. We know that if the unit digit of the cube is 1, the unit digit of the cube root must be 1 (1 × 1 × 1 = 1). So, we get 1 at the unit’s place of the cube root.

Step 3: The second group has the only digit 1. Hence the required ten’s digit of the cube root is 1.

Step 4: Hence, ∛1331 = 11.

(ii) 4913

Step 1: We start making groups of three digits starting from the rightmost digit. Therefore, first group = 913 and second group is 4.

Step 2: The first group will give you the unit’s digit of the required root. We know that if the unit digit of the cube is 3, the unit digit of the cube root must be 7 (7 × 7 × 7 = 343). So, we get 7 at the unit’s place of the cube root.

Step 3: The second group has the only digit 4. We know 1³ < 4 < 2³. So we take the lower limit as the ten’s digit.

Step 4: Hence, ∛4913 = 17.

(iii) 12167

Step 1: We start making groups of three digits starting from the rightmost digit. Therefore, first group = 167 and second group is 12.

Step 2: The first group will give you the unit’s digit of the required root. We know that if the unit digit of the cube is 7, the unit digit of the cube root must be 3 (3 × 3 × 3 = 27). So, we get 3 at the unit’s place of the cube root.

Step 3: The second group is 12. We know 2³ < 12 < 3³. So, we take 2 as the ten’s digit.

Step 4: Hence, ∛12167 = 23.

(iv) 32768

Step 1: We start making groups of three digits starting from the rightmost digit. Therefore, first group = 768 and second group is 32.

Step 2: The first group will give you the unit’s digit of the required root. We know that if the unit digit of the cube is 8, the unit digit of the cube root must be 2 (2 × 2 × 2 = 8). So, we get 2 at the unit’s place of the cube root.

Step 3: The second group is 32. We know 3³ < 32 < 4³. So, we take 3 as the ten’s digit.

Step 4: Hence, ∛32768 = 32.

Extra Questions to Complement Solutions to NCERT Class 8 Mathematics Chapter 6 Cubes and Cube Roots:

Very Short Answer Type:

1. What is the smallest number that can be expressed as the sum of two cubes in two different ways.
Answer:
The required number is 1729.

We see that, 1729 = 1728 + 1 = 12³ + 1 and 1729 = 10³ + 9³.

2. If a = b³ find the value of b.
Answer:
a = b³ or b³ = a or b = ∛a (Taking the cube root).

3. What is the digit in the unit’s place of the cube root of 4096?
Answer:
We know that if the unit digit of the cube is 6, the unit digit of the cube root must be 6 (6 × 6 × 6 = 216). The digit in the unit’s place of the cube root of 4096 is 6.

4. Tell by mere observation which of ∛512 and ∛729 is greater.
Answer:
Since 729 > 512 the cube root of 729 will also be greater than 512. Therefore,∛729 is greater.

5. Tell by mere observation if 800 is a perfect cube.
Answer:
No 800 is not a perfect cube. Perfect cubes which end with zeros must contain at least 3 zeroes at the end. But 800 only contains 2 zeroes.

6. Is there a unique cube root for every number?
Answer:
Yes there is a unique cube root for every number, including negative numbers.

7. Name an integer which does not increase or decrease when it is cubed.
Answer:
0 is an integer which does not increase or decrease when it is cubed.

8. What is the smallest integral perfect cube greater than 800?
Answer:
We see that 9³ = 729. Therefore, we take the next digit 10. We see that 10³ = 1000 which is greater than 800. Therefore, the smallest integral perfect cube greater than 800 is 1000.

9. Is there a limit to the number of times a number can be cubed.
Answer:
No, a number can be cubed countless times.

10. Write all perfect cubes between 100 and 200.
Answer:
125 is the only perfect cube between 100 and 200.

Multiple Choice Questions:

1. The surface area of a cube is 256 square units. What is the volume of the cube.

(a) 5096
(b) 4096
(c) 3096
(d) 256

Answers: Correct answer:(b) 4096.

The length of each side of the cube is a. Therefore, the surface area = a².

a² = 256 or a =∛256 = 16

a² = 256 or a = √256 = 16.

Volume of the cube = a³.

Therefore,

a³ = (16)³ = 4096 cubic units.

2. If we divide the cube of a non-zero integer with its square, what do we get?

(a) The number itself
(b) The division is not possible
(c) 0
(b) Depends on the specific case.

Answer: Correct answer: (a) The number itself.

Let the number be a. Therefore, a³ ÷ a² = a³/a² = a. This is the number itself.

3. What can you say about the cube of 729?

(a) Ends with the digit 1 and is even
(b) Ends with the digit 9 and is odd
(c) Ends with the digit 9 and is even
(d) Ends with the digit 1 and is odd.

Answer: Correct answer:(b) Ends with the digit 9 and is odd. When a number ending with 9 is cubed, the last digit of the cubed number is 9. Also, cubes of all odd numbers are odd. Since 729 is odd the cube will also be odd.

4. The value of (1.3)³ is:

(a) 2.197
(b) 21.97
(c) 2197
(d) 0.2197

Answer: Correct answer: (a) 2.197.

5. Represent 10³ and 12³ on a number line. Which of the following is correct?

(a) 10³ is to the right of 12³
(b) 10³ is to the left of 12³
(c) They are right next to each other.
(d) They are far away from each other

Answer: Correct answer: (b) and (d).

Short and Long Answer Type Questions:

1. Express (1 + 3 + 5 + 7 + 9 + 11) as the sum of cubes.

Answer: We can see that:

1 = 1 = 1³ …………………………(i)

3 + 5 = 8 = 2³……………………(ii)

7 + 9 + 11 = 27 = 3³………….(iii)

Adding (i), (ii) and (iii) we get:

1 + 3 + 5 + 7 + 9 + 11 = 1³ + 2³ + 3³ which is the sum of three cubes.

2. Consider the following pattern.

2³ – 1³ = 1 + 2 × 1 × 3

3³ – 2³ = 1 + 3 × 2 × 3

4³ – 3³ = 1 + 4 × 3 × 3

Using the above pattern find the value of the following:

(i) 12³ – 11³                     (ii) 20³ – 19³                (iii) 51³ – 50³

Answers:

(i) 12³ – 11³

Using the pattern we get:

12³ – 11³

= 1 + 12 × 11 × 3

= 1 + 396

= 397 (Answer)

(ii) 20³ – 19³

Using the pattern we get:

20³ – 19³

= 1 + 20 × 19 × 3

= 1 + 1140

= 1141 (Answer)

(iii) 51³ – 50³

Using the pattern we get:

51³ – 50³

= 1 + 51 × 50 × 3

 = 1 + 7650 = 7651 (Answer)

3. State true or false: for any fraction m, m² < m³. Give explanation.

Answer:

Let us take the fraction 1/2.

m² = (1/2)² = 1/4

m3 = (1/2)³ = 1/8

Since 1/4 > 1/8, we can say m² > m³.

In general, when a fraction is cubed its denominator becomes greater than when it is squared. Since the denominator becomes greater, the fraction becomes smaller when it is cubed than when it is squared.

Hence in general we can say, m² > m³ for any fraction m. Hence the above statement is False.

. Three numbers are in the ratio 1:2:3 and the sum of their cubes is 4500. Find the numbers. (NCERT Exemplar)

Answer: Let the three number be x, 2x and 3x.

Sum of their cubes is 4500.

Therefore,

x³ + (2x)³ + (3x)³ = 4500

or, x³ + 8x³ + 27x³ = 4500

or, 36x³ = 4500

or, x³ = 125

or, x = ∛125

or, x = 5.

2x = 10, 3x = 15.

The required numbers are 5, 10 and 15.

5. The edge length of a cube is doubled. Find the percentage increase in the volume.

Answer: Let the original length of the cube be x.

The original volume = x³.

The new edge length is 2x.

The new volume = (2x)³ = 8x³.

Therefore, the volume increases by a percentage of (8x³– x³)/x³ × 100 = 7x³/x³ × 100 = 700%.

6. How many consecutive odd integers will be needed to obtain the sum as 10³?

Answer: We can see the following pattern:

1 = 1³

3 + 5 = 2³

7 + 9 + 11 = 3³

13 + 15 + 17 + 19 = 4³

We can see that the number of digits in LHS = number that is raised to the power 3 on RHS. Therefore, 10 consecutive odd numbers will be needed in LHS to obtain 10³ in RHS.

7. Find the smallest perfect cube number which is divisible by each of 3, 6, 8.

Answer: Let us first find the smallest number which is divisible by each of 3, 6, 8. This is the LCM of 3, 6, 8.

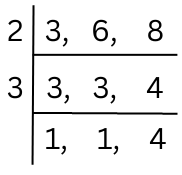
LCM = 2 × 3 × 4 = 24.

Prime factorisation of 24 = 2 × 2 × 2 × 3. (Grouping into triplets).

There is an isolated 3 which is not grouped. Hence, we have to multiply by 3 × 3 to get a cubed number.

24 × 3 × 3 = 2 × 2 × 2 × 3 × 3 × 3. This is a perfect cube because the like factors exist in triplets.

Therefore, required number = 216.

So, the smallest perfect cube number which is divisible by each of 3, 6, 8 is 216.

8. Show that (a + b)(a² – ab + b²) is the sum of two cubed numbers.

Answer:

(a + b)(a² – ab + b²)

= a(a² – ab + b²) + b(a² – ab + b²)

= a³ – a²b + ab² + a²b – ab² + b³

= a³ + b³, which is the sum of two cubed numbers

9. The cube root of 6860 lies close to which number? Estimate without actually finding square root.

Answer: Let us start with 18³.

18³ = 5832 which is not very close to 6860.

Now we take 19³ = 6859 which is very close to 6860.

Therefore, the cube root of 6860 lies close to 19.

10. Calculate the sum of (1³ + 2³ + 3³ + 4³ + 5³) without finding the cubes.

Answer:

We can write:

1³ = 1

2³ = 3 + 5

3³ = 7 + 9 + 11

4³ = 13 + 15 + 17 + 19

5³ = 21 + 23 + 25 + 27 + 29

Adding we get,

1³ + 2³ + 3³ + 4³ + 5³ = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29

There are 15 consecutive odd numbers starting from 1 in the RHS.

We know that sum of n consecutive odd numbers starting from 1 = n².

Therefore,

 1³ + 2³ + 3³ + 4³ + 5³ = 15² = 225 (Answer)

Fill in the Blanks:

(a) The sum of the cubes of two consecutive integers is 1729. The integers are ____________ and ____________.

(b) If the like factors in the prime factorisation of a number do not exist in triplets, then the number is not a ____________.

(c) if on cubing a number the number decreases, then the number can be a ____________.

(d) You can identify the unit’s digit of a cubed number from observing the ____________ of the number itself.

(e) ___________ numbers exist which can be expressed as the sum of two cubes in two different ways.

Answers:

(a) The sum of the cubes of two consecutive integers is 1729. The integers are 9 and 10.

(b) If the like factors in the prime factorisation of a number do not exist in triplets, then the number is not a cube.

(c) if on cubing a number the number decreases, then the number can be a fraction.

(d) You can identify the unit’s digit of a cubed number from observing the unit’s digit of the number itself.

(e) Infinite numbers exist which can be expressed as the sum of two cubes in two different ways.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 8 Mathematics Chapter 6 Cubes and Cube Roots: