Hello students and welcome to the crucial chapter on Work and Energy! It is essential that you grasp the concepts of this chapter early on and be able to solve numericals on your own. By answering all in-text questions, exercise questions and activities we have answered all your questions on this chapter. We have even included an extra problem set which will show you problem-solving techniques and clear your concepts. The illustrations will also make learning interesting for you! So, let’s dive in!
Solutions to In Text Questions of NCERT Class 9 Science Chapter 10 Work and Energy –
Page 115:
1. A force of 7 N acts on an object. The displacement is, say 8 m, in the direction of the force (Fig. 10.3). Let us take it that the force acts on the object through the displacement. What is the work done in this case?
Answer:
When a force F acting on an object causes a displacement s, work is done on the body by the force.
Work done = Force × Displacement
or, W = F × s
In this case, F = 7 N and s = 8 m.
W = 7 × 9 = 56 Nm = 56 J.
Page 116:
1. When do we say that work is done?
Answer:
Work is done when a force acting on a body displaces the body in the direction of the force. Work is also done when a retarding force acts opposite to the direction of motion of a body and causes it to stop.
2. Write an expression for the work done when a force is acting on an object in the direction of its displacement.
Answer:
When a force F acting on an object causes a displacement s in the direction of the applied force, work done (W) = F × s.
3. Define 1 J of work.
Answer:
1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.
4. A pair of bullocks exerts a force of 140 N on a plough. The field being ploughed is 15 m long. How much work is done in ploughing the length of the field?
Answer:
Force (F) = 140 N and displacement (s) = 15 m.
Work done (W) = F × s = 140 N × 15 m = 2100 J.
Therefore, the work done in ploughing the length of the field = 2100 J.
Page 119:
1. What is the kinetic energy of an object?
Answer:
Kinetic energy is the energy produced by a body by virtue of its motion. Kinetic energy of a body moving with a certain velocity is equal to the work done on it to make it acquire that velocity.
2. Write an expression for the kinetic energy of an object.
Answer:
The kinetic energy possessed by an object of mass, m and moving with a uniform velocity, v is Ek = (1/2)mv2.
3. The kinetic energy of an object of mass, m moving with a velocity of 5 m s–1 is 25 J. What will be its kinetic energy when its velocity is doubled? What will be its kinetic energy when its velocity is increased three times?
Answer:
Ek = 25 J
Velocity (v) = 5 m s–1
Let mass be m.
Therefore,
Ek = (1/2)mv2
or, (1/2) × m × 52 = 25
or, m = 2 kg
When velocity is doubled,
v = 10 ms-1
m = 2 kg
Therefore,
Ek = (1/2)mv2 = (1/2) × 2 × 102 = 100 J
When velocity is increased 3 times,
v = 15 ms-1
m = 2 kg
Therefore,
Ek = (1/2)mv2 = (1/2) × 2 × 152 = 225 J
Page 123:
1. What is power?
Answer:
Power is defined as the rate of doing work or the rate of transfer of energy. If an agent does a work W in time t, then power is given by: Power = work/time or P = W/t.
2. Define 1 watt of power.
Answer:
1 watt is the power of an agent, which does work at the rate of 1 joule per second. 1 watt = 1 joule/second or 1 W = 1 J s–1.
3. A lamp consumes 1000 J of electrical energy in 10 s. What is its power?
Answer:
Power is defined as the rate of doing work or the rate of transfer of energy.
Here energy consumed = 1000 J. Time = 10 s.
Power = 1000 J/10 s = 100 J/s = 100 Watt.
4. Define average power.
Answer:
Average power is defined as the total work done or total energy consumed or transferred by the total time taken.
Solutions to Exercises (Page No 124) of NCERT Class 9 Science Chapter 10 Work and Energy
1. Look at the activities listed below. Reason out whether or not work is done in the light of your understanding of the term ‘work’.
• Suma is swimming in a pond.
• A donkey is carrying a load on its back.
• A wind-mill is lifting water from a well.
• A green plant is carrying out photosynthesis.
• An engine is pulling a train.
• Food grains are getting dried in the sun.
• A sailboat is moving due to wind energy.
Answer:
Work is done when there is a net force acting on the body and a displacement is caused by the force in or opposite to the direction of motion.
(i) Suma exerts a force on the water and by Newton’s third law the water exerts and equal and opposite force on Suma. This force causes displacement. Hence, work is done.
(ii) When a donkey carries a load, it exerts an upward force to counteract gravity, but the displacement of the load is in the forward direction. Because the force and displacement are perpendicular to each other, the work done is zero.
(iii) The windmill exerts a force in the upward direction and the motion of the water is also in the upward direction. Hene, there is work done.
(iv) During photosynthesis there is no force and no displacement. Hence, work is not done.
(v) An engine exerts a force on the train in the forward direction and the train moves in the forward direction. Hence work is done.
(vi) When food grains are getting dried in the sun, there is no net force and no net displacement. Hence, no work is done.
2. An object thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and the final points of the path of the object lie on the same horizontal line. What is the work done by the force of gravity on the object?
Answer:
Work done by the force of gravity on the object depends only on the vertical displacement.
Work Done = Force × Displacement
or, Work Done = mg × 0 (Since vertical displacement = 0)
or, Work done = 0 J.
Therefore, work done by the force of gravity on the object is 0 J.
3. A battery lights a bulb. Describe the energy changes involved in the process.
Answer:
When a bulb is connected to a battery, the chemical energy of the battery is converted into electrical energy. Subsequently, the bulb transforms this electrical energy into both light and heat energy. Therefore, the energy transformation in this scenario can be represented as follows: Chemical Energy → Electrical Energy → Light Energy + Heat Energy
4. Certain force acting on a 20 kg mass changes its velocity from 5 m s–1 to 2 m s–1. Calculate the work done by the force.
Answer:
Mass of the body = 20 kg
Initial velocity (u) = 5 m s-1
Final velocity v = 2 m s-1
Thus, initial kinetic energy
Ei = (1/2) mu2 = (1/2) × 20 × (5)2
= 250 J
Final kinetic energy
Ef = (1/2) mv2 = (1/2) × 20 × (2)2
= 10 × 4
= 40 J
Therefore,
Work done = Change in kinetic energy
Work done = Ef – Ei
Work done = 40 J – 250 J
Work done = -210 J
The negative sign indicates that the direction of force is opposite to the direction of motion.
5. A mass of 10 kg is at a point A on a table. It is moved to a point B. If the line joining A and B is horizontal, what is the work done on the object by the gravitational force? Explain your answer.
Answer:
Work done by the force of gravity on the object depends only on the vertical displacement. Here the displacement is horizontal or vertical displacement = 0.
Work Done = Force × Displacement
or, Work Done = mg × 0 (Since vertical displacement = 0)
or, Work done = 0 J.
Therefore, work done by the force of gravity on the object is 0 J.
6. The potential energy of a freely falling object decreases progressively. Does this violate the law of conservation of energy? Why?
Answer:
No, it does not violate the law of conservation of energy as the potential energy gets converted into kinetic energy. As the potential energy decreases, the kinetic energy of the object gradually increases. The total mechanical energy which is the sum of kinetic energy and potential energy remains conserved.
7. What are the various energy transformations that occur when you are riding a bicycle?
Answer:
When you ride a bicycle the muscular energy is converted into heat energy and kinetic energy. The kinetic energy drives the bicycle forward and the heat energy heats up our body.
8. Does the transfer of energy take place when you push a huge rock with all your might and fail to move it? Where is the energy you spend going?
Answer:
No, transfer of energy does not take place since there is no displacement of the rock. The muscular energy you spend gets converted into heat energy and heats up your body.
9. A certain household has consumed 250 units of energy during a month. How much energy is this in joules?
Answer:
1 unit of energy = 1 kWh
250 units = 250 kWh
1 kWh = 3.6 × 106 J
Therefore,
250 units = 250 × 3.6 × 106 J = 9 × 108 J.
10. An object of mass 40 kg is raised to a height of 5 m above the ground. What is its potential energy? If the object is allowed to fall, find its kinetic energy when it is half-way down.
Answer:
Mass (m) = 40 kg.
Acceleration due to gravity (g) = 10m s-2
Height above the ground (h) = 5 m
Potential energy= mgh = 40 × 10 × 5 = 2000 J
When it is half-way down, the height above the ground = 5/2 = 2.5 m.
Potential energy when it is halfway down = mgh = 40 × 10 × 2.5 = 1000 J.
According to law of conservation of energy,
Total potential energy at 10 m height = potential energy halfway down at 5 m height + kinetic energy halfway down at 5 m height
or, 2000 J = 1000 J + kinetic energy halfway down at 5 m height
or, Kinetic energy halfway down at 5 m height = 2000 J – 1000 J = 1000 J.
11. What is the work done by the force of gravity on a satellite moving round the earth? Justify your answer.
Answer:
Work done by the force of gravity on the object depends only on the vertical displacement. When a satellite moves round the earth the direction of motion at every point is perpendicular to the force of gravity which is towards the centre. Hence, the vertical displacement = 0 and work done by the force of gravity is zero.
12. Can there be displacement of an object in the absence of any force acting on it? Think. Discuss this question with your friends and teacher.
Answer:
Displacement of an object can occur even without the presence of an external force. Consider a scenario where an object is moving at a constant velocity. Although the net force acting on the object is zero, it still undergoes displacement during its motion. Hence, displacement can indeed occur without the necessity of a force.
13. A person holds a bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not? Justify your answer.
Answer:
The person holding the bundle of hay over his head has not done any work because the displacement of the bundle of hay is zero.
Work Done = Force × Displacement = Force × 0 = 0.
14. An electric heater is rated 1500 W. How much energy does it use in 10 hours?
Answer:
Power of the heater = 1500 W = 1.5 kW.
Time taken = 10 hours.
Power = Energy consumed/Time
or, Energy consumed = Power × Time
or, Energy consumed = 1.5 kW × 10 hr
or, Energy consumed = 15 kW h.
15. Illustrate the law of conservation of energy by discussing the energy changes which occur when we draw a pendulum bob to one side and allow it to oscillate. Why does the bob eventually come to rest? What happens to its energy eventually? Is it a violation of the law of conservation of energy?
Answer:
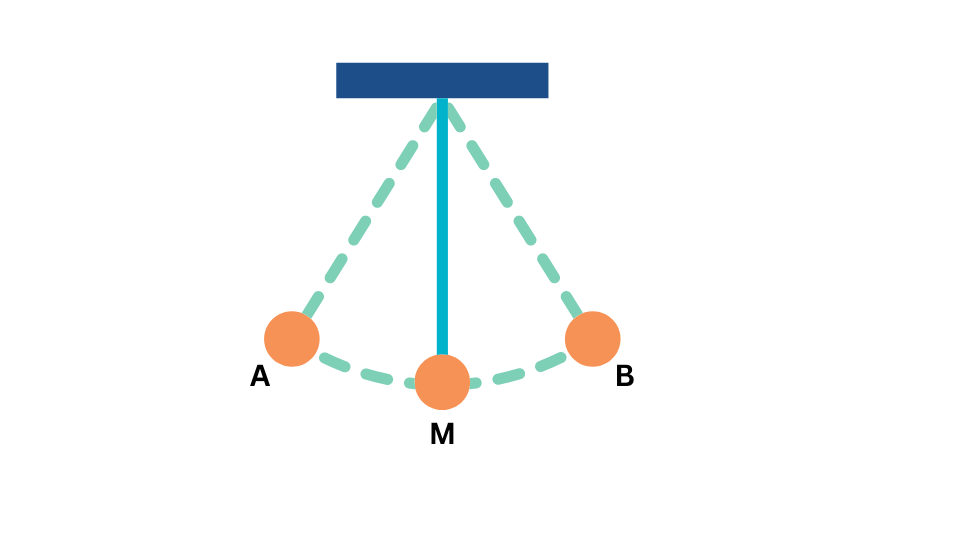
Potential Energy to Kinetic Energy Conversion: As we draw the pendulum bob to one side from the mean position M, it gains potential energy due to its increased height above its mean position. This potential energy is converted into kinetic energy as the bob is released and starts to swing. At the lowest point of its swing at M, when it reaches its maximum speed, all of its potential energy has been converted into kinetic energy.
Kinetic Energy to Potential Energy Conversion: As the pendulum bob swings upwards, its kinetic energy decreases and is converted back into potential energy. At the highest point of its swing at A, when it momentarily stops before changing direction, all of its kinetic energy has been converted into potential energy.
Conservation of Mechanical Energy: Thus, we can see thatthroughout the motion of a pendulum the total mechanical energy i.e. sum of kinetic energy and potential energy is conserved. Thus, the law of conservation of energy holds.
The bob eventually comes to rest because of air resistance. Air resistance saps the kinetic energy of the pendulum, causing its motion to slow down. The kinetic energy is converted into thermal energy due to friction with the air and leads to a slight increase in temperature in the vicinity of the pendulum. Thus, the law of conservation of energy holds and energy is not destroyed.
16. An object of mass, m is moving with a constant velocity, v. How much work should be done on the object in order to bring the object to rest?
Answer:
Work done = Change in kinetic energy of the object.
Work done = Final K.E – Initial K.E
or, work done = 0 – (1/2)mv2
or, Work done = – (1/2)mv2
The negative sign indicates that the force is opposing the direction of motion.
17. Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km/h?
Answer:
Velocity = 60 km/h = 60000m/3600s = 16.67 m/sec.
Work done = Change in kinetic energy of the object.
Work done = Final K.E – Initial K.E
or, work done = 0 – (1/2)mv2
or, Work done = – (1/2)mv2
or, Work done = – (1/2) × 1500 kg × (16.67)2
or, Work done = – 208416.68 J
18. In each of the following a force, F is acting on an object of mass, m. The direction of displacement is from west to east shown by the longer arrow. Observe the diagrams carefully and state whether the work done by the force is negative, positive or zero.

Answer:
From left to right:
Block 1: The direction of the force is perpendicular to the direction of displacement. Hence, work done by the force on the block is zero.
Block 2: The direction of the force is in the same direction as the direction of displacement. Hence, work done by the force on the block is positive.
Block 3: The direction of the force is in a direction opposite to the direction of displacement. Hence work done by the force on the block is negative.
19. Soni says that the acceleration in an object could be zero even when several forces are acting on it. Do you agree with her? Why?
Answer:
Yes, acceleration of an object could be zero even when several forces are acting on it if the net force acting on the body is zero. The forces can cancel each other out and the net force becomes zero. In this case, the body can be at rest or in a state of uniform motion.
20. Find the energy in joules consumed in 10 hours by four devices of power 500 W each.
Answer:
Power consumed = 500 W = 0.5 kW.
Time taken = 10 hours.
For one device:
Power = Energy consumed/Time
or, Energy consumed = Power × Time
or, Energy consumed = 0.5 kW × 10 hr = 5 kWh
Therefore, total energy consumes by four such devices = 4 × 5 = 20 kWh.
21. A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy?
Answer: Just before reaching the ground, the potential energy of the freely falling object will get completely converted into kinetic energy. On hitting the ground, this kinetic energy converts into heat energy, sound energy and also may be used to deform the surface. As a result, the law of conservation of energy holds.
Solutions to All Activities of NCERT Class 9 Science Chapter 10 Work and Energy –
1. Complete Activity 10.1 (Page 113). We have discussed in the above paragraphs a number of activities which we normally consider to be work in day-to-day life. For each of these activities, ask the following questions and answer them:
(i) What is the work being done on?
(ii) What is happening to the object?
(iii) Who (what) is doing the work?
Answer:
2. Complete Activity 10.2 (Page 114).
• Think of some situations from your daily life involving work.
• Discuss with your friends whether work is being done in each situation.
• Try to reason out your response.
• List them.
• If work is done, which is the force acting on the object?
• What is the object on which the work is done? • What happens to the object on which work is done?
Answer:
3. Complete Activity 10.3 (Page 114).
• Think of situations when the object is not displaced in spite of a force acting on it.
• Also think of situations when an object gets displaced in the absence of a force acting on it.
• List all the situations that you can think of for each.
• Discuss with your friends whether work is done in these situations.
Answer:
4. Complete Activity 10.4 (Page 115).
• Lift an object up. Work is done by the force exerted by you on the object. The object moves upwards. The force you exerted is in the direction of displacement. However, there is the force of gravity acting on the object.
• Which one of these forces is doing positive work?
• Which one is doing negative work?
• Give reasons.
Answer:
5. Complete Activity 10.5 (Page 116).
• A few sources of energy are listed above. There are many other sources of energy. List them.
• Discuss in small groups how certain sources of energy are due to the Sun. • Are there sources of energy which are not due to the Sun?
Answer:
6. Complete Activity 10.6 (Page 117).
• Take a heavy ball. Drop it on a thick bed of sand. A wet bed of sand would be better. Drop the ball on the sand bed from height of about 25 cm. The ball creates a depression.
• Repeat this activity from heights of 50 cm, 1m and 1.5 m.
• Ensure that all the depressions are distinctly visible.
• Mark the depressions to indicate the height from which the ball was dropped.
• Compare their depths.
• Which one of them is deepest?
• Which one is shallowest? Why?
• What has caused the ball to make a deeper dent?
• Discuss and analyse.
Answer:
7. Complete Activity 10.7 (Page 117).
• Set up the apparatus as shown in Fig. 10.5.
• Place a wooden block of known mass in front of the trolley at a convenient fixed distance.
• Place a known mass on the pan so that the trolley starts moving.
• The trolley moves forward and hits the wooden block.
• Fix a stop on the table in such a manner that the trolley stops after hitting the block. The block gets displaced.
• Note down the displacement of the block. This means work is done on the block by the trolley as the block has gained energy.
• From where does this energy come?
• Repeat this activity by increasing the mass on the pan. In which case is the displacement more?
• In which case is the work done more?
• In this activity, the moving trolley does work and hence it possesses energy.
Answer:
8. Complete Activity 10.8 (Page 119).
• Take a rubber band.
• Hold it at one end and pull from the other. The band stretches.
• Release the band at one of the ends.
• What happens?
• The band will tend to regain its original length. Obviously the band had acquired energy in its stretched position.
• How did it acquire energy when stretched?
Answer:
9. Complete Activity 10.9 (Page 119).
• Take a slinky as shown below.
• Ask a friend to hold one of its ends. You hold the other end and move away from your friend. Now you release the slinky.
• What happened?
• How did the slinky acquire energy when stretched?
• Would the slinky acquire energy when it is compressed?
Answer:
10. Complete Activity 10.10 (Page 119).
• Take a toy car. Wind it using its key.
• Place the car on the ground.
• Did it move?
• From where did it acquire energy?
• Does the energy acquired depend on the number of windings? • How can you test this?
Answer:
11. Complete Activity 10.11 (Page 119).
• Lift an object through a certain height. The object can now do work. It begins to fall when released.
• This implies that it has acquired some energy. If raised to a greater height it can do more work and hence possesses more energy. • From where did it get the energy? Think and discuss.
Answer:
12. Complete Activity 10.12 (Page 119).
• Take a bamboo stick and make a bow as shown in Fig. 10.6.
• Place an arrow made of a light stick on it with one end supported by the stretched string.
• Now stretch the string and release the arrow.
• Notice the arrow flying off the bow. Notice the change in the shape of the bow. • The potential energy stored in the bow due to the change of shape is thus used in the form of kinetic energy in throwing off the arrow.
Answer:
13. Complete Activity 10.13 (Page 121).
• Sit in small groups.
• Discuss the various ways of energy conversion in nature.
• Discuss following questions in your group:
(a) How do green plants produce food?
(b) Where do they get their energy from?
(c) Why does the air move from place to place?
(d) How are fuels, such as coal and petroleum formed?
(e) What kinds of energy conversions sustain the water cycle?
Answer:
14. Complete Activity 10.14 (Page 121).
• Many of the human activities and the gadgets we use involve conversion of energy from one form to another.
• Make a list of such activities and gadgets. • Identify in each activity/gadget the kind of energy conversion that takes place.
Answer:
15. Complete Activity 10.15 (Page 122).
An object of mass 20 kg is dropped from a height of 4 m. Fill in the blanks in the following table by computing the potential energy and kinetic energy in each case.
| Height at which object is located m | Potential energy (Ep = mgh) J | Kinetic energy (Ek = mv2/2) J | Ep + Ek J |
| 4 | |||
| 3 | |||
| 2 | |||
| 1 | |||
| Just above the ground |
Answer:
16. Complete Activity 10.16 (Page 122).
• Consider two children, say A and B. Let us say they weigh the same. Both start climbing up a rope separately. Both reach a height of 8 m. Let us say A takes 15 s while B takes 20 s to accomplish the task.
• What is the work done by each?
• The work done is the same. However, A has taken less time than B to do the work.
• Who has done more work in a given time, say in 1 s?
Answer:
17. Complete Activity 10.17 (Page 123).
• Take a close look at the electric meter installed in your house. Observe its features closely.
• Take the readings of the meter each day at 6.30 am and 6.30 pm.
• Do this activity for about a week.
• How many ‘units’ are consumed during day time?
• How many ‘units’ are used during night?
• Tabulate your observations.
• Draw inferences from the data.
• Compare your observations with the details given in the monthly electricity bill (One can also estimate the electricity to be consumed by specific appliances by tabulating their known wattages and hours of operation).
Answer:
Extra Questions to Complement Solutions to NCERT Class 9 Science Chapter 10 Work and Energy –
Very Short Answer Type:
1. You push a car. What kind of energy does it have?
Answer:
Kinetic energy.
2. You lift a ball to a certain height. What kind of energy does the ball have?
Answer:
Potential energy.
3. You lift a ball to a certain height. Who/what is doing the work?
Answer:
You are doing the work on the ball.
4. A spring is stretched. What kind of energy does the spring have?
Answer:
Potential energy.
5. What is the biggest natural source of energy to us?
Answer:
The sun.
6. What is the commercial unit of energy?
Answer:
Kilowatt hour (kWh).
7. When birds fly what are the types of energy they possess?
Answer:
Kinetic energy and potential energy.
8. What is 1 unit of energy equivalent to?
Answer:
1 Kilowatt hour (kWh).
9. Name two renewable sources of energy.
Answer:
Solar energy, wind energy.
10. The unit of heat was named after which scientist?
Answer:
James Prescott Joule.
Multiple Choice Questions (MCQ):
1. When a ball is thrown upwards through a certain height, the total energy:
(A) Increases
(B) Decreases
(C) Remains constant
(D) Fist increases then decreases
Answer: (C) Remains constant
The total energy of the ball remains constant. The kinetic energy gets converted into potential energy as the ball rises. Then the potential energy is converted into kinetic energy as the ball falls back down.
2. A body of mass 10 kg is lifted through a height of 10 m. A second body of mass 5 kg is lifted through a height of 15 m. Which one has more energy?
(A) First body
(B) Second body
(C) Both are equal
(D) Depends on the value of acceleration due to gravity
Answer: (A) First body
Potential energy of first body = 10 × 10 × 10 = 1000 J.
Potential energy of second body = 5 × 10 × 15 = 750 J.
Since 1000 J > 750 J, the potential energy of first body is greater than the potential energy of second body.
3. An iron sphere of mass 10 kg has the same diameter as an aluminium sphere of mass is 3.5 kg. Both spheres are dropped simultaneously from a tower. When they are 10 m above the ground, they have the same (NCERT Exemplar)
(A) acceleration
(B) momenta
(C) potential energy
(D) kinetic energy
Answer: (A) acceleration
The acceleration due to gravity does not depend on the mass of the bodies. The momenta, potential energy and kinetic energy all depend on the mass of the bodies.
4. A wound-up spring in a clock possesses:
(A) No energy
(B) Electrical energy
(C) Kinetic energy
(D) Potential energy
Answer: (D) Potential energy
5. A train accelerates to a velocity which is 4 times the initial velocity on levelled tracks. The potential energy of the train:
(A) does not change
(B) becomes twice to that of initial
(C) becomes 4 times that of initial
(D) becomes 16 times that of initial
Answer: (A) does not change
The height of the train above the levelled tracks does not change, hence the potential energy of the train does not change.
Short Answer Type:
1. An object of mass m is dropped from a height h. Find the velocity of the object just before reaching the ground. (Hint: Use the principle of conservation of energy)
Answer:
At height h, potential energy of the object = mgh.
Let velocity of the object just before reaching the ground be v.
Therefore, kinetic energy of the object just before reaching the ground = (1/2)mv2.
According to principle of conservation of energy,
(1/2)mv2 = mgh
or, v2 = 2gh
or, v = √2gh
The velocity of the object just before reaching the ground = √2gh.
2. An object of mass 10 kg is moving with velocity 10 m/s comes to rest at a certain distance. Is this a violation of the law of conservations of energy? Explain.
Answer:
When the object comes to rest, its kinetic energy is converted into other forms of energy, such as thermal energy due to friction. Hence, the principle of conservation of energy is not violated.
3. An object of mass 10 kg has momentum of 20 kg m/s. What is the kinetic energy of the object?
Answer:
Momentum = mass (m) × velocity (v)
or, 20 = 10 × velocity (v)
or, velocity (v) = 2 m/s
Kinetic energy = (1/2)mv2 = (1/2) × 10 × 22 = 20 J
4. A car of mass 5 kg is initially at rest and accelerates from 0 m/s to 20 m/s over a distance of 50 meters. Calculate the work done by the car’s engine.
Answer:
Work done by the engine = change in kinetic energy of the car.
Initial kinetic energy = (1/2)m(0)2 = 0 J.
Final kinetic energy = (1/2)(5)(20)2 = 1000 J.
Therefore, work done by the engine = Final kinetic energy – Initial kinetic energy = 1000 J – 0 J = 1000 J.
5. Can an object have kinetic energy without having any potential energy? Justify your answer.
Answer:
A car moving along a straight road can have kinetic energy but zero potential energy because it is at zero height above the ground.
6. A toy car of mass 0.5 kg was pressed against a spring and released. The initial velocity of the car was 20 m/s. Calculate the potential energy stored in the spring.
Answer:
Mass of the car (m) = 0.5 kg.
Initial velocity (v) = 20 m/s.
Initial kinetic energy of car = (1/2)mv2 = (1/2) × 0.5 × 202 = 100 J.
Potential energy stored in the spring = Initial kinetic energy of car = 100 J.
7. A wind turbine generates 500 kWh of electricity in a day. Calculate the average power output of the wind turbine in kW.
Answer:
Average power = Energy generated/Time
Energy generated = 500 kWh
Time = 1 day = 24 h
or, Average power = Energy generated/Time = 500 kWh/24h = 20.83 kW.
8. A body of mas 5 kg moving with velocity 10 m/s comes to a stop at distance of 50 m under the action of a retarding force. What is the value of the retarding force? Use principle of conservation of energy to solve this problem.
Answer:
Final kinetic energy = (1/2)m(0)2 = 0 J.
Initial kinetic energy = (1/2) × 5 × (10)2 = 250 J.
Change in kinetic energy = Final kinetic energy – Initial kinetic energy = 0 J – 250 J = -250 J.
The change in kinetic energy = work done by the retarding force.
Let the retarding force be F.
The displacement is 50 m.
Therefore,
-250 J = F (-50)
or, F = 5 N.
Therefore, the value of the retarding force is 5 N.
9. A machine applies a force of 1000 N to move a crate horizontally across the floor with a constant velocity of 2 m/s. Calculate the power exerted by the machine.
Answer:
Let force be F and displacement be s.
Work done (W) = F × s
Power = Work done (W)/Time
Let time be t.
Power = F × s/t
Or, Power = F × v (Where velocity v = s/t).
Therefore, in this case:
Power = 1000 N × 2 m/s = 2000 watt = 2 kW.
10. You are whirling a stone tied to one end of a thread. What is the work done by the centripetal force on the stone?
Answer:
The work done by the centripetal force on the stone is zero. The centripetal force acts towards the centre of the circle and is perpendicular to the direction of motion of the stone at every point, which is tangential to the circle. Therefore, the work done by the centripetal force is 0.
Long Answer Type:
1. A ball of mass 1 kg is released from a height of 10 m. On hitting the ground the ball bounces a height of 5 m. How much energy is lost on hitting the ground?
Answer:
Potential energy = mgh where m is the mass, g is the acceleration due to gravity and h is the height.
Initial potential energy at height 10 m = 1 × 10 × 10 = 100 J.
On hitting the ground the ball bounces a height of 5 m.
The final potential energy after hitting the ground and rebounding to a height of 5 m = 1 × 10 × 5 = 50 J.
Therefore, the energy lost on hitting the ground = Final potential energy – initial potential energy = 100 J – 50 J = 50 J.
2. A mass of 5 kg is lifted to a height 10 m and another mass of 5 kg is lifted to a same height. Then they are tied together at that height and released. Find the velocity with which the combined mass hits the ground. Take g = 9.8 m/s2.
Answer:
The potential energy of each mass at height 10 m = mgh, where m is the mass, g is the acceleration due to gravity and h is the height.
The total potential energy = 2mgh.
The mass of the combined particle = 2m = 2 × 5 = 10 kg.
The kinetic energy of the combined particle when it hits the ground = (2m)v2, where v is the velocity with which the combined particle hits the ground.
Therefore,
(1/2)(2m)v2 = 2mgh
or, v2 = 2gh
or, v2 = 2 × 9.8 × 10
or, v2 = 196
or, v = 14 m/s
Therefore, the velocity with which the combined particle hits the ground is 14 m/s.
Fill in the Blanks:
(a) 5 kWh = __________ J
(b) When a force is applied to an object and it moves in the direction of the force, work is said to be ___________.
(c) The work done by the force of gravity on a speeding car is ____________.
(d) The sum of the kinetic and potential energies of an object is called its ___________ energy.
(e) If the velocity of an object is tripled, its kinetic energy increased by __________ times.
Answers:
(a)5 kWh = 1.8 × 107 J.
(b)When a force is applied to an object and it moves in the direction of the force, work is said to be positive.
(c) The work done by the force of gravity on a speeding car is 0.
(d) The sum of the kinetic and potential energies of an object is called its mechanical energy.
(e) If the velocity of an object is tripled, its kinetic energy increased by 9 times.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 9 Science Chapter 10 Work and Energy
Did you wish you had the solutions to all the exercise questions, in-text questions and activities all in one place? We have it right here for you! Alongside these solutions, we have also provided you with a set of extra problems for additional practice. Also, we have included the PDF versions of the solutions which you can download anytime for free!
Like what we offer and want more from us? Keep visiting our website and subscribe to our email list to be among the first to access all the latest goodies! (insert hyperlink)
The following topics are covered:
10.1 Work
10.2 Energy
10.3 Rate of Doing Work
Here are the number of questions for the chapter:
(i) 14 Theoretical Questions (Questions 1, 2, 3, 5, 6, 7, 8, 11, 12, 13, 15, 18, 19, 21)
(ii) 7 Numerical-based Questions (Questions 4, 9, 10, 14, 16, 17, 20)
Understand the concept of work, kinetic energy and potential energy and the interconversion between them. The concept of power is also equally important. The best way to master this chapter is to solve theoretical and numerical problems of many kinds. This will clear your concepts and give you confidence. Our solutions and extra problem set are an excellent place to start practising.
Anytime you need expert coaching, our personable faculty will be there for you. They use systematic training methods and will get you ready for any exam. Contact us anytime with your requirements and let us help you out! (Insert hyperlink)
Our personable team of experts is here to guide and support you every step of the way. Whether you need coaching, mentoring, or just a helping hand, we’re dedicated to helping you reach your full potential. With personalized one-on-one sessions tailored to your schedule and needs, we’re here to make sure you succeed – your way! So don’t hesitate to reach out to us anytime (insert hyperlink) – let’s work together to achieve your goals!


