Hello there students! Chapter 7 Motion is a fundamental chapter in physics and it is vital that you master it not just for your exams, but also for higher classes. We have answered all in-text questions, exercise questions, in-text activities in this comprehensive solutions material. These solutions have been meticulously crafted to simplify complex concepts and boost your understanding. Dive into Chapter 7 with confidence, armed with extra practice questions to sharpen your skills and ace your exams.
Solutions to In Text Questions of NCERT Class 9 Science Chapter 7 Motion
Page 74:
1. An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.
Answer:
An object which has moved through a distance can have zero displacement if it comes back to its initial position. For example, if a car moves along a circular track and comes back to where it started, the displacement of the car will be zero.
2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Answer:
Perimeter of the square field = 4 × 10 = 40 m.
The farmer takes 40 s to cover a distance of 40 m.
Therefore, in 1 s he covers a distance of 1 m.
Therefore, at the end of 2 minutes 20 seconds or 140 s he covers a distance of 140 m.
The number of rounds he covers in 2 minutes 20 seconds or 140 s = 140/40 = 3.5.
Therefore, in the figure below if the farmer starts from initial position O, at the end of 3.5 rounds he will be at position B.
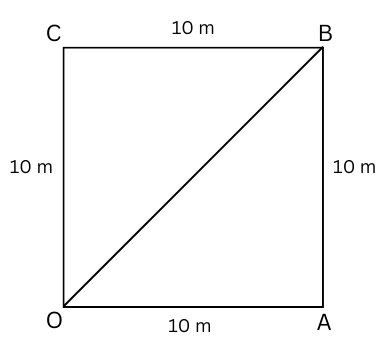
Therefore, displacement from O = √((OA)2 + (AB)2) = √((10)2 +(10)2) = √200 = 10√2 = 14.14 m.
The magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position = 14.14 m.
3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Answer:
(a) It cannot be zero.
False. When an object travels a certain distance and returns to its initial position, the displacement of the object is 0.
(b) Its magnitude is greater than the distance travelled by the object.
False. Magnitude of displacement can be equal to or less than the distance travelled by the object.
Page 76:
1. Distinguish between speed and velocity.
Answer:
Speed is how fast an object moves, measured as the distance travelled per unit of time, and has no direction. Velocity includes both the speed and direction of motion.
2. Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Answer:
We know that average velocity = total displacement/total time and average speed = total distance/total time. Therefore, the magnitude of average velocity of an object is equal to its average speed when the total displacement of an object = total distance covered by it in a given time period. This happens only when an object moves along a straight line without turning back.
3. What does the odometer of an automobile measure?
Answer:
The odometer of an automobile measures the total distance travelled by the vehicle since it was last reset, providing a cumulative measure of distance.
4. What does the path of an object look like when it is in uniform motion?
Answer:
The path of an object looks like a straight line when it is uniform motion.
5. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is, 3 × 108 m s–1.
Answer:
The signal travels in a straight line, so the distance of the spaceship from the ground station is equal to the distance travelled by the signal.
5 minutes = 5 × 60 = 300 seconds.
Speed of light = 3 × 108 m s–1.
Therefore, total distance = 3 × 108 m s–1 × 300 s = 9 × 1010 m.
Page 77:
1. When will you say a body is in (i) uniform acceleration? (ii) non uniform acceleration?
Answer:
(i) Uniform acceleration:
If an object travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time, then the acceleration of the object is said to be uniform. The motion of a freely falling body is an example of uniformly accelerated motion.
(ii) non uniform acceleration
On the other hand, an object can travel with non-uniform acceleration if its velocity changes at a non-uniform rate. For example, if a car travelling along a straight road increases its speed by unequal amounts in equal intervals of time, then the car is said to be moving with non-uniform acceleration.
2. A bus decreases its speed from 80 km h–1 to 60 km h–1 in 5 s. Find the acceleration of the bus.
Answer:
Initial velocity of the bus (u) = 80 km/hour = 80000 m/3600s = 22.22 m.s-1
Final velocity of the bus (v) = 60 km/hour = 60000 m/3600s = 16.66 m.s-1
Time taken, t = 5 seconds.
Therefore, acceleration (a) = (v – u)/t = (16.66 m.s-1 – 22.22 m.s-1)/5s = -1.11 m.s-2
Summary: A bus decreases its speed from 80 km h–1 to 60 km h–1 in 5 s. The acceleration of the bus = -1.11 m.s-2. Negative acceleration indicates that the bus is slowing down, i.e. its speed is decreasing.
3. A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h–1 in 10 minutes. Find its acceleration.
Answer:
Initial velocity (u) = 0. Final velocity (v) = 40 km h–1 = 40000m/3600s = 11.11 m/s.
Time taken (t) = 10 minutes = 10 × 60 = 600 s.
Therefore, acceleration (a) = (v – u)/t = (11.11 – 0)/600 m.s-2 = 0.0185 m.s-2.
Page 81:
1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer:
The distance-time graph for uniform motion of an object is a straight line. The distance-time graph for non-uniform motion of an object is a curve.
2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Answer:
When the distance-time graph is a straight line parallel to the time axis, it means that the distance does not change with time. Therefore, the object is at rest.
3. What can you say about the motion of an object if its speed time graph is a straight line parallel to the time axis?
Answer:
If the speed time graph is a straight line parallel to the time axis, it means that the speed does not change with time. Therefore, the object is in uniform motion.
4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer:
Displacement is the quantity which is measured by the area occupied below the velocity-time graph.
Page 82:
1. A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. Find (a) the speed acquired, (b) the distance travelled.
Answer:
(a) Since the bus starts from rest,initial velocity (u) = 0.
Acceleration (a) = 0.1 m s-2
Time = 2 minutes = 120 s.
Let final velocity be v.
v = u + at
or, v = 0 + 0.1 m s-2 × 120 s = 12 m.s-1
(b) Let distance covered be s.
2as = v2 – u2
or, s = (v2– u2)/2a = (122– 02)/(2 × 0.1) = 720 m
Therefore, distance travelled = 720 m.
Summary: A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. (a) The speed acquired is 12 m.s-1, (b) the distance travelled = 720 m.
2. A train is travelling at a speed of 90 km h–1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s-2. Find how far the train will go before it is brought to rest.
Answer:
Initial velocity (u) = 90 km/hour = 90000/3600 = 25 m.s-1
Final velocity (v) = 0 m.s-1
Acceleration (a) = -0.5 m.s-2
We know, v2 – u2 = 2as
Therefore, distance travelled by the train (s) = (v2– u2)/2a = (02– 252)/(2 ×(-0.5)) = 625 m
Summary:
A train is travelling at a speed of 90 km h–1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s-2. The train will go 625 m before it is brought to rest.
3. A trolley, while going down an inclined plane, has an acceleration of 2 cm s-2. What will be its velocity 3 s after the start?
Answer:
The trolley starts from rest, initial velocity (u) = 0.
Acceleration (a) = 2 cm s-2 = 0.02 m.s-2
Time (t) = 3 s.
Final velocity (v) = 0 m.s-1
Therefore,
v = u + at = 0 + (0.02 m.s-2)(3 s) = 0.06 m.s-1 = 6 cm.s-1.
Summary:
A trolley, while going down an inclined plane, has an acceleration of 2 cm s-2. The velocity 3 s after the start is 6 cm.s-1.
4. A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start?
Answer:
The racing car is initially at rest. Initial velocity (u) = 0.
Acceleration (a) = 4 m s-2.
Time (t) = 10 s.
Let distance covered be s.
Therefore,
s = ut + (1/2)at2 = (0)t + × 4 × (10)2 = 200 m.
Summary: A racing car has a uniform acceleration of 4 m s-2. The distance it will cover in 10 s after starting is 200 m.
5. A stone is thrown in a vertically upward direction with a velocity of 5 m s-1. If the acceleration of the stone during its motion is 10 m s–2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Answer:
Initial velocity (u) = 5 m s-1.
Acceleration (a) = – 10 m s–2.
Final velocity (v) = 0 as the stone attains a state of rest at the point of maximum height.
Let height attained by the stone be s.
We know, v2 – u2 = 2as Therefore, distance travelled by the train (s) = (v2– u2)/2a = (02– 52)/(2 × (-10)) = 625 m
Let time taken to cover the distance be t.
v = u + at
or, t = (v – u)/a = (0 – 5)/(-10) = 0.5 s.
Summary: A stone is thrown in a vertically upward direction with a velocity of 5 m s-1. If the acceleration of the stone during its motion is 10 m s–2 in the downward direction, the height attained by the stone is 1.25 m and time taken to reach there is 0.5 s.
Solutions to Exercises (Page No 85) of NCERT Class 9 Science Chapter 7 Motion
1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Answer:
Diameter of the track (d) = 200 m.
Circumference of the track = πd = 200π.
Distance covered in 40 s is 200π.
Distance covered in 1 s is 200π/40.
Distance covered in 2 minutes 20 s or 140 s = (200π/40 × 140) = ((200 )/40 × (22 )/7 × 140) = 2200 m.
Number of rounds completed by the athlete in 2 minutes 20 s or 140 s = 140/40 = 3.5.
Therefore, the final position of the athlete is at the opposite end of the circular track with respect to his starting position.
Therefore, the displacement = diameter of the circular track = 200 m.
Summary:
An athlete completes one round of a circular track of diameter 200 m in 40 s. The distance covered and the displacement at the end of 2 minutes 20 s are 2200 m and 200 m respectively.
2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer:
(a) Distance from A to B is 300 m.
Displacement from A to B = 300 m.
Time taken to cover the distance = 2 minutes 30 seconds = 150 seconds.
Average speed = total distance/time = 300m/150 seconds = 2 ms-1.
Average velocity = total displacement/time = 300m/150 seconds = 2 ms-1.
(b) Total distance from A to C is 300 m + 100 m = 400 m.
Displacement from A to C = 300 m – 100 m = 200 m.
Time taken to cover the distance = 2 minutes 30 seconds + 1 minute = 210 seconds.
Average speed = total distance/time = 400m/210 seconds = 1.9 ms-1.
Average velocity = total displacement/time = 200m/210 seconds = 0.95 ms-1.
Summary:
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. Joseph’s average speeds and velocities in jogging (a) from A to B are both 2 m.s-1 and Joseph’s average speeds and velocities in jogging (b) from A to C are 1.9 ms-1 and 0.95 ms-1 respectively.
3. Abdul, while driving to school, computes the average speed for his trip to be 20 km h–1. On his return trip along the same route, there is less traffic and the average speed is 30 km h–1. What is the average speed for Abdul’s trip?
Answer:
Distance covered to each school = distance covered to reach home = d.
Let time taken to reach school be t1.
Let time taken to reach home be t2. Average speed while going to school = (Total distance travelled)/(Total time taken) = d/t1 = 20.
Therefore, t1 = d/20.
Average speed while returning = (Total distance travelled)/(Total time taken) = d/t2 = 30.
Therefore, t2 = d/30.
Now, average speed for the whole trip = (Total distance travelled)/(Total time taken) = (d + d)/(t1+ t2)
= 2d/(d/20 + d/30)
= 2/(1/20 + 1/30)
= 2/((3 + 2)/60)
= 2 × 60/5
= 24 km h–1
Summary: Abdul, while driving to school, computes the average speed for his trip to be 20 km h–1. On his return trip along the same route, there is less traffic and the average speed is 30 km h–1. The average speed for Abdul’s trip is 24 km h–1.
4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s–2 for 8.0 s. How far does the boat travel during this time?
Answer:
Initial velocity of the motorboat (u) = 0.
Acceleration (a) = 3.0 m s–2.
Time period (t) = 8 s.
Let distance covered by the boat be s.
Therefore,
s = ut + at2
or, s = 0 + × 3 × 82
or, s = 96 m
Summary:
A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s–2 for 8.0 s. The boat travels 96 m during this time.
5. A driver of a car travelling at 52 km h–1 applies the brakes Shade the area on the graph that represents the distance travelled by the car during the period. (b) Which part of the graph represents uniform motion of the car?
Answer:
(a) The area on the graph that represents the distance covered by the car during the period when the brakes are applied is shown below:
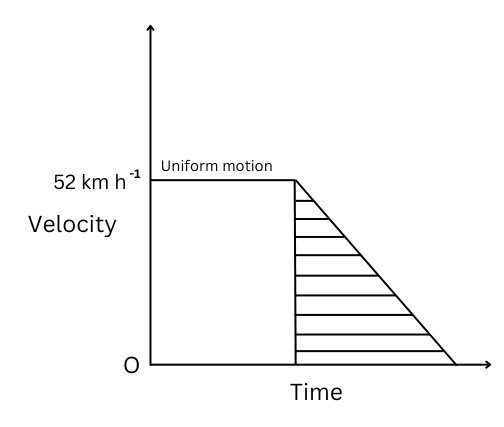
(b) The part of the graph that represents uniform motion of the car is shown above.
6. Fig 7.10 shows the distance-time graph of three objects A, B and C. Study the graph and answer the following questions:
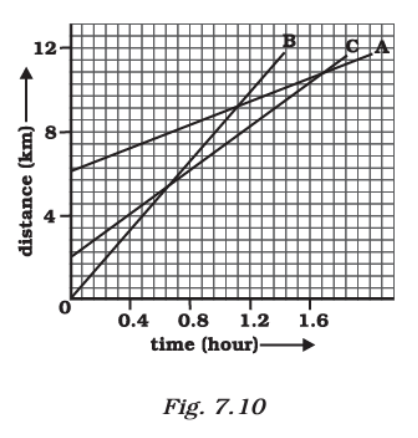
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?
Answer:
(a) Car B is travelling the fastest because it covers the greatest distance in the time interval.
(b) All three are never at the same point on the road because the three lines do not intersect at one point.
(c) Since there are 7 units between 0 and 4 on the y-axis, 1 graph unit equals 4/7 km.
Object C is initially 4 graph units away from the origin on the y-axis. Therefore, its initial distance from the origin is 4 × (4/7) km = 16/7 km.
At the time when B passes A, C will have covered a distance of 8 km.
Therefore, total distance travelled till when B passes A = 8 – (16/7) km = 5.71 km.
(d) By the time it passes C, B will have travelled 9 graph units.
Therefore, distance travelled by B is 9 × (4/7) km = 5.14 km.
7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground? After what time will it strike the ground?
Answer:
Since the ball was initially at rest, initial velocity of the ball (u) = 0.
Distance travelled by ball (s) = 20 m.
Acceleration (a) = 10 m.s-2
Let final velocity be v.
We know,
v2 – u2 = 2as
or, v2 = 2 × 10 m.s-2 × 20 m + 0
or, v2 = 400 m2.s-2
or, v = 20 m.s-1
Let the time taken for it to strike the ground be t.
We know:
v = u + at
or, t = (v – u)/a
or, t = (20 – 0)/10
or, t = 2 s
Summary:
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, the velocity with which it strikes the ground is 20 m.s-1 and the time taken to strike the ground is 2 s.
8. The speed-time graph for a car is shown is Fig. 7.11.
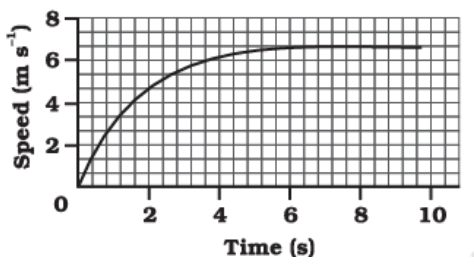
(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer:
(a) The area of the graph that represents the distance travelled by the car during the 4 seconds is shown below:
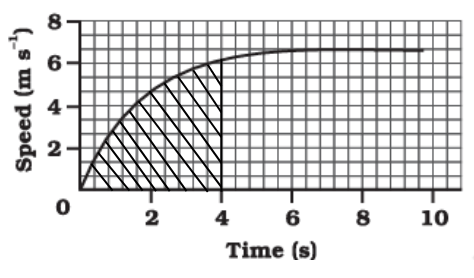
The shaded region can be approximated as a triangle and the area of the triangle will give us the distance travelled in the first 4 seconds.
Distance = 1/2 × 4 × 6 = 12 m.
(b) The speed of the car does not change between the 6th second to the 10th second. Therefore, the part between the 6th second to the 10th second represents uniform motion of the car.
9. State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity
(b) an object moving with an acceleration but with uniform speed.
(c) an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer:
(a) This is possible. When an object is thrown upwards and reaches maximum height, the velocity is zero but the object has constant acceleration due to force of gravity acting on it.
(b) This is possible. An object moving in a circle with uniform speed has acceleration because the direction of motion changes at every point, thereby resulting in change in velocity.
(c) This is possible. A satellite orbiting the Earth moves in a direction tangential to its orbit at every point, but experiences acceleration towards the Earth due to gravity, which acts perpendicular to its direction of motion.
10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer:
The radius of the orbit of satellite = 42250 km.
Therefore, circumference of the orbit = 2πr = 2 × π × 42250 km = 265571.43 km.
Time to revolve around the earth = 24 hours.
Therefore, speed of the satellite = 265571.43 km/24 hours = 11065.5 km.h-1
Summary: An artificial satellite is moving in a circular orbit of radius 42250 km. If it takes 24 hours to revolve around the earth, its speed is 11065.5 km.h-1.
Solutions to All Activities of NCERT Class 9 Science Chapter 7 Motion
1. Complete Activity 7.1 (Page 72). Discuss whether the walls of your classroom are at rest or in motion.
Answer:
2. Complete Activity 7.2 (Page 72).
• Have you ever experienced that the train in which you are sitting appears to move while it is at rest? • Discuss and share your experience.
Answer:
3. Complete Activity 7.3 (Page 73).
• Take a metre scale and a long rope.
• Walk from one corner of a basket-ball court to its opposite corner along its sides.
• Measure the distance covered by you and magnitude of the displacement.
• What difference would you notice between the two in this case?
Answer:
4. Complete Activity 7.4 (Page 73).
• Automobiles are fitted with a device that shows the distance travelled. Such a device is known as an odometer. A car is driven from Bhubaneshwar to New Delhi. The difference between the final reading and the initial reading of the odometer is 1850 km. • Find the magnitude of the displacement between Bhubaneshwar and New Delhi by using the Road Map of India.
Answer:
5. Complete Activity 7.5 (Page 74).
• The data regarding the motion of two different objects A and B are given in Table 7.1.
• Examine them carefully and state whether the motion of the objects is uniform or non-uniform.
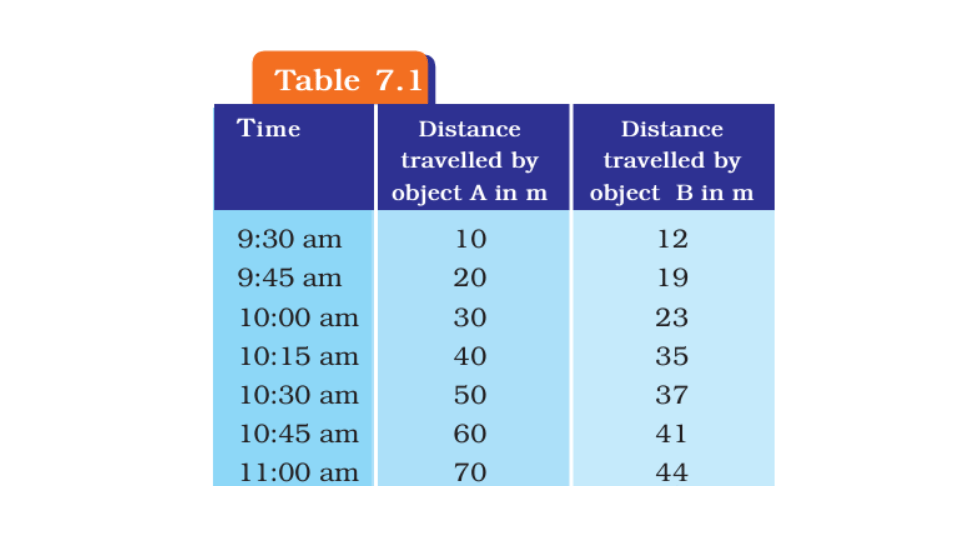
Answer:
6. Complete Activity 7.6 (Page 75). Measure the time it takes you to walk from your house to your bus stop or the school. If you consider that your average walking speed is 4 km h–1, estimate the distance of the bus stop or school from your house.
Answer:
7. Complete Activity 7.7 (Page 76).
• At a time when it is cloudy, there may be frequent thunder and lightning. The sound of thunder takes some time to reach you after you see the lightning.
• Can you answer why this happens?
• Measure this time interval using a digital wrist watch or a stop watch. • Calculate the distance of the nearest point of lightning. (Speed of sound in air = 346 m s-1.)
Answer:
8. Complete Activity 7.8 (Page 77).
• In your everyday life you come across a range of motions in which
(a) acceleration is in the direction of motion,
(b) acceleration is against the direction of motion,
(c) acceleration is uniform,
(d) acceleration is non-uniform.
• Can you identify one example each for the above type of motion?
Answer:
9. Complete Activity 7.9 (Page 80).
The times of arrival and departure of a train at three stations A, B and C and the distance of stations B and C from station A are given in Table 7.4.
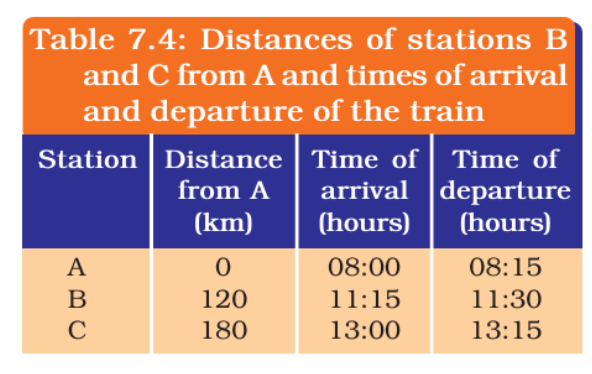
Plot and interpret the distance-time graph for the train assuming that its motion between any two stations is uniform.
Answer:
10. Complete Activity 7.10 (Page 81).
Feroz and his sister Sania go to school on their bicycles. Both of them start at the same time from their home but take different times to reach the school although they follow the same route. Table 7.5 shows the distance travelled by them in different times
| Table 7.5: Distance covered by Feroz and Sania at different times on their bicycles | ||
| Time | Distance travelled by Feroz (km) | Distance travelled by Sania (km) |
| 8.00 am | 0 | 0 |
| 8.05 am | 1.0 | 0.8 |
| 8.10 am | 1.9 | 1.6 |
| 8.15 am | 2.8 | 2.3 |
| 8:20 am | 3.6 | 3.0 |
| 8:25 am | – | 3.6 |
Plot the distance-time graph for their motions on the same scale and interpret.
Answer:
11. Complete Activity 7.11 (Page 84).
• Take a piece of thread and tie a small piece of stone at one of its ends. Move the stone to describe a circular path with constant speed by holding the thread at the other end, as shown in Fig. 7.9.
• Now, let the stone go by releasing the thread.
• Can you tell the direction in which the stone moves after it is released? • By repeating the activity for a few times and releasing the stone at different positions of the circular path, check whether the direction in which the stone moves remains the same or not.
Answer:
Extra Questions to Complement Solutions to NCERT Class 9 Science Chapter 7 Motion
Very Short Answer Type Questions:
1. Give the SI unit of displacement.
Answer:
Metre.
2. Area under the graph for a velocity-time graph gives us which quantity?
Answer:
Displacement.
3. A body is moving with constant velocity in a straight line. What is its acceleration?
Answer:
Zero.
4. Name a tissue in our body that is in constant motion.
Answer:
Blood.
5. What is the magnitude of acceleration due to gravity?
Answer:
9.8 m s-2
6. A ball is dropped from a certain height. What is its initial velocity?
Answer:
Zero.
7. A car moves along a winding road. Its speed remains constant. Is its velocity constant for the whole journey?
Answer:
No, because the direction changes.
8. What does the slope of the velocity-time graph give us?
Answer:
Acceleration.
9. The distance-time graph of a car is a straight line. What can you say about its velocity?
Answer:
Velocity is uniform.
10. An athlete takes 2 seconds to move along a semicircular path of radius 2 m. What is its speed?
Answer:
Speed = πr/t = (π × 2)/2 = π m s-1
Short Answer Type Questions:
1. A car travels 10 km every 1 hour. What can you say about its motion? What can you say about its acceleration?
Answer:
The car is in uniform motion since it covers equal distances in equal intervals of time. The acceleration of the car = 0.
2. A ball is thrown vertically upwards. What is the time to reach the maximum height?
Answer:
We know, v = u + at.
The ball reaches maximum height when final velocity becomes 0.
Here a = -g, v = 0.
Therefore,
0 = u – gt or,
t = u/g
3. A car accelerates from rest at a constant rate of 2 m s-2 for a time of 5 s. Determine:
(a) The final velocity of the car.
(b) The average velocity of the car during this time
Answer:
(a) We know, v = u + at
Initial velocity u = 0, a = 2, t = 5.
v = 0 + 2 × 5
or, v = 10 m s-1
Final velocity = 10 m s-1.
(b) Average velocity = (u + v)/2 = (0 + 10)/2 = 5 m s-1.
4. A car moves three-quarters of the circumference along a circular path of radius r. What is its displacement?
Answer:
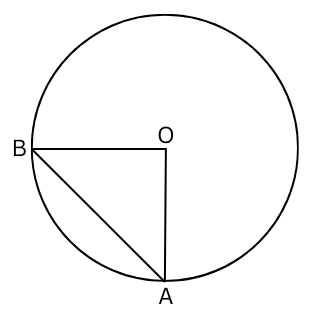
If the car starts from A and moves three-quarters of the circumference it will reach B.
The displacement AB = √((OA)2 + (OB)2) = √(r2+ r2 ) = √(2r2 ) = √2r.
5. A car moves along a circular path with constant speed. Is the acceleration of the car zero?
Answer:
Although the speed of the car is uniform, the velocity of the car changes at every point due to change in the direction of motion. Therefore, the car has acceleration.
6. The velocity-time graph of a car is shown below. What can you say about the acceleration?
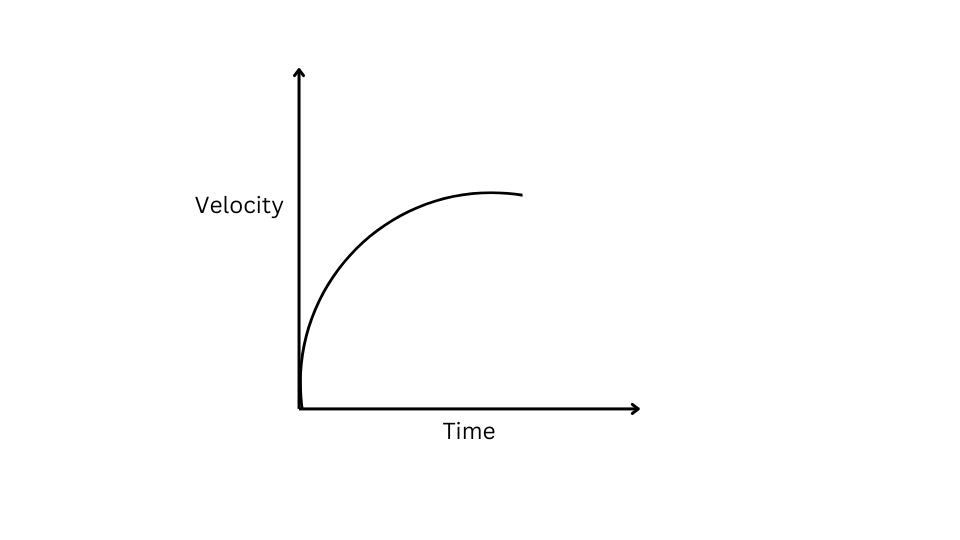
Answer:
We can see from the graph that the rate of change of velocity is decreasing over time. Therefore, the car has negative acceleration or retardation.
7. A ball is thrown vertically upwards with an initial velocity of 15 ms-1. Determine: (a) How long it takes for the ball to return to its initial position. (b) What is the displacement of the ball during this time?
Answer:
(a) First let us find the time taken to reach the maximum height.
We know v = u + at.
Here, v = 0, u = 15 ms-1, a = -9.8 ms-2
Therefore,
0 = 15 – 9.8t
or, t = 15/9.8 = 1.53 seconds
Therefore, time taken to reach the maximum height = 1.53 seconds. Time taken to return to its initial position will be double that of that.
Therefore, time taken to return to its initial position = 1.53 × 2 = 3.06 seconds.
(b) Since the ball returns to its initial position, the displacement = 0.
8. A car is moving along a straight road. After a certain point its acceleration varies with time as (-t3 + t2) where t is time. What can you say about the acceleration?
Answer:
The expression (-t3 + t2) is always negative. As time increases, the acceleration becomes even more negative. So, in this case, the acceleration of the car is continuously decreasing with time, meaning the car is experiencing deceleration or retardation along the straight road.
9. A train starts from rest and accelerates uniformly at 2 m/s2 for 10 s. After that, it decelerates uniformly at 1 m/s2 until it comes to rest. The total time taken for the train to come to rest.
Answer:
Let us find the velocity of the train after 10 s.
v = u + at
or, v = 0 + 2 × 10
or, v = 20 m/s
Thus, 20 m/s is the initial velocity for the deceleration period and final velocity = 0.
For the deceleration period, v = 0, u = 20 m/s, a = 1 m/s2.
v = u – at
or, 0 = 20 – 1t
or, t = 20 s.
Therefore, the train decelerates for 20 s and accelerates for 10 s. Therefore, total time taken for the train to come to rest = 20 s + 10 s = 30 s.
10. Can a velocity-time graph be circular?
Answer:
No, a velocity-time graph cannot be circular because it would mean that two velocities would exist at the same instant.
Long Answer Type Questions:
1. Two balls are thrown vertically upwards. Their initial velocities are in the ratio 1:2. What is the ratio of the heights reached by the two balls?
Answer:
Let the velocity of the first ball be u and the second ball be 2u.
Let height attained by the first ball be h1.
We know,
v2 – u2 = 2gh1
or, 02 – u2 = 2gh1
or, h1 = u2/2g
Let height attained by the first ball be h2.
v2 – u2 = 2gh1
or, 02 – (2u)2 = 2gh2
or, h2 = 4u2/2g
h1/h2 = u2/2g ÷ 4u2/2g
or, h1/h2 = 1:4
2. A rocket is launched vertically upwards. Its acceleration as a function of time is given by a(t) = 10 – 2t, where a is in m/s² and t is in seconds. Determine: (a) The initial acceleration of the rocket. (b) The time it takes for the rocket to reach zero acceleration. (c) What happens to the rocket’s acceleration after it reaches zero?
Answer:
(a) We get the initial acceleration by putting t = 0 in a(t) = 10 – 2t.
Putting t = 0, a(t) = 10 – 2 × 0 = 10 m/s²
Initial acceleration = 10 m/s².
(b) Putting a(t) = 0, we get:
0 = 10 – 2t
or, t = 10/2 = 5 seconds.
Therefore, it takes 5 s for the rocket to reach zero acceleration.
(c) After it reaches zero, the rocket’s acceleration becomes negative. This indicates that the rocket experiences a negative acceleration, or deceleration. Therefore, the rocket starts to slow down after reaching zero acceleration.
Fill in the Blanks:
(a) When acceleration is negative it is called ___________.
(b) When the velocity of an object changes with respect to time, it is said to be undergoing ___________.
(c) In a velocity-time graph, a horizontal line represents ___________ acceleration or deceleration.
(d) If an object is accelerating uniformly, its velocity-time graph will be a ___________ line.
(e) A body undergoes uniform motion starting from rest. Its final velocity is 10 ms-1. The average velocity for the journey is __________.
Answers:
(a) When acceleration is negative it is called retardation.
(b) When the velocity of an object changes with respect to time, it is said to be undergoing acceleration.
(c) In a velocity-time graph, a horizontal line represents zero acceleration or deceleration.
(d) If an object is accelerating uniformly, its velocity-time graph will be a straight line.
(e) A body undergoes uniform motion starting from rest. Its final velocity is 10 ms-1. The average velocity for the journey is 5 ms-1.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 9 Science Chapter 7 Motion
Our meticulously crafted solutions material covers all in-text questions, exercises, and activities. Complemented with captivating illustrations our material ensures a seamless understanding of every concept. Dive deeper with our additional problem set, perfect for boosting your exam preparation. Plus, enjoy the convenience of accessing free PDF downloads of all solutions anytime, anywhere!
Excited to stay ahead with our latest materials and exclusive offers? Keep visiting our website regularly and subscribe to our email list for updates and special promotions. (insert hyperlink)
The following topics are covered:
7.1 Describing Motion
7.2 Measuring the Rate of Motion
7.3 Rate of Change of Velocity
7.4 Graphical Representation of Motion
7.5 Equations of Motion
7.6 Uniform Circular Motion
Here are the number of problems for the chapter:
(i) 7 Numerical-based Questions (Questions 1 – 5, 7, 10)
(ii) 2 Graph-based Questions (Questions 6, 8)
(iii) 1 Theoretical Questions (Questions 9)
The best way to understand the concepts in this chapter is to practise numericals and graph-based questions. Study the equations of motion and graphs in the textbook well, you will see questions from this material in the exams. As always, we have included an extra problem-set which will give you additional practice.
Looking for expert coaching that’s tailored just for you? Don’t hesitate to reach out anytime (Insert hyperlink) – we’re here to provide the personalized guidance you need to succeed!
Embark on a journey of growth and achievement with our personalized coaching services. Let us be your guiding light as you navigate through your academic and professional endeavours. Reach out to us whenever you need support or advice – we’re here to help you shine! We provide expert one-on-one coaching and mentoring to you depending on your convenience and needs – have it completely your way!


