Hello students and welcome to Class 7! We have prepared excellent solutions to NCERT Class 7 Math Chapter 1 Integers for you to study. Our experts have done an excellent job of explaining the concepts to you and have even included extra questions of various formats for you to practise. This solutions material follows the latest NCERT syllabus and will be an excellent place to start if you are looking to study integers.
Solutions to Exercise 1.1 (Page No 4) of NCERT Class 7 Math Chapter 1 Integers:
1. Following number line shows the temperature in degree celsius (co) at different places on a particular day.

Answer:
By observing the number line, we can see that the gap between two successive marks represents 1o. Therefore, the temperatures of the places marked on it are shown as follows:
| Lahulspiti | -8o C |
| Srinagar | -2o C |
| Shimla | 5o C |
| Ooty | 14o C |
| Bengaluru | 22o C |
(b) What is the temperature difference between the hottest and the coldest places among the above?
Answer:
From the number line, we can see that the temperature of the hottest place (Bengaluru) = 22o C
Also, the temperature of the coldest place = -8o C
Therefore, the temperature difference between the hottest and the coldest places = 22o C – (-8o C)
For subtraction, we add the additive inverse of the integer that is being subtracted to the other integer. Therefore, a – (-b) = a + additive inverse of (-b) = a + b
So, 22o C – (-8o C) = 22o C + 8o C = 30 o C
(c) What is the temperature difference between Lahulspiti and Srinagar?
Answer:
From the number line we can see that:
The temperature of Lahulspiti = -8o C
The temperature of Srinagar = -2o C
The temperature difference between Lahulspiti and Srinagar = -2o C – (-8o C)
For subtraction, we add the additive inverse of the integer that is being subtracted to the other integer. Therefore, a – (-b) = a + additive inverse of (-b) = a + b
So, -2o C – (-8o C) = -2o C + 8o C = 6o C
(d) Can we say the temperature of Srinagar and Shimla, taken together, is less than the temperature in Shimla? Is it also less than the temperature in Srinagar?
Answer:
From the number line we can see that:
The temperature of Srinagar = -2o C
The temperature of Shimla = 5o C
Therefore, the temperature of Srinagar and Shimla taken together = -2o C + 5o C = 3 o C.
Since, 3 o C < 5o C, the temperature of Srinagar and Shimla, taken together, is indeed less than the
temperature in Shimla.
Since, 3 o C > -2o C, the temperature of Srinagar and Shimla, taken together, is not less than the temperature in Srinagar.
2. In a quiz, positive marks are given for correct answers and negative marks are given for incorrect answers. If Jack’s scores in five successive rounds were 25, – 5, – 10, 15 and 10, what was his total at the end?
Answer:
Jack’s scores in five successive rounds are: 25, – 5, – 10, 15 and 10.
Jack’s total score at the end = 25 + (-5) + (-10) + 15 + 10 = 25 – 5 – 10 + 15 + 10 = 35.
3. At Srinagar temperature was – 5°C on Monday, and then it dropped by 2°C on Tuesday. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by 4°C. What was the temperature on this day?
Answer:
On Monday, the temperature at Srinagar = – 5°C.
Then it dropped by 2°C on Tuesday.
Therefore, on Tuesday, the temperature at Srinagar = – 5°C – 2°C = – 7°C.
On Wednesday, it rose by 4°C. Therefore, the temperature on Wednesday = – 7°C + 4°C = – 3°C.
4. A plane is flying at the height of 5000 m above sea level. At a particular point, it is exactly above a submarine floating 1200 m below sea level. What is the vertical distance between them?

Answer:
The sea-level is taken as 0 m.
The height of the plane above sea-level will be represented by a positive integer.
Therefore, the distance above sea-level = 5000 m.
The distance below sea-level will be represented by a negative integer.
Therefore, the depth of the submarine below sea-level = – 1200 m.
So, the vertical distance between them = 5000 – (– 1200) m.
For subtraction, we add the additive inverse of the integer that is being subtracted to the other integer. Therefore, a – (-b) = a + additive inverse of (-b) = a + b
Therefore, 5000 – (– 1200) = 5000 + 1200 = 6200 m.
5. Mohan deposits ₹ 2,000 in his bank account and withdraws ₹ 1,642 from it the next day. If the withdrawal of the amount from the account is represented by a negative integer, then how will you represent the amount deposited? Find the balance in Mohan’s account after the withdrawal.
Answer:
The withdrawal of the amount from the account is represented by a negative integer.
Therefore, the amount deposited can be represented by a positive integer.
The amount of money Mohan deposits in his bank account = ₹ 2,000.
And, the amount of the money Mohan withdraws the next day = – ₹ 1,642.
Therefore, the balance in Mohan’s account after the withdrawal = Amount of money deposited + Amount of money withdrawn = ₹ 2,000 + (– ₹ 1,642) = ₹ 2,000 – ₹ 1,642 = ₹ 358.
6. Rita goes 20 km towards the east from point A to point B. From B, she moves 30 km towards the west along the same road. If the distance towards the east is represented by a positive integer, then how will you represent the distance travelled towards the west? By which integer will you represent her final position from A?

Answer:
The distance towards the east is represented by a positive integer.
Therefore, the distance towards the west (opposite to east) is represented by a negative integer.
The distance Rita goes towards the east = 20 km.
After that, the distance Rita goes towards the west = – 30 km.
Therefore, her final position from A = 20 + (– 30) = 20 – 30 = – 10 km (which is a negative integer) and is to the west of A.
7. In a magic square, each row, column and diagonal have the same sum. Check which of the following is a magic square.
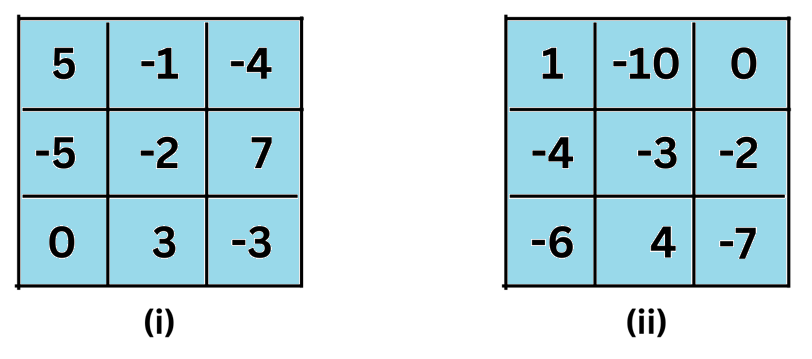
Answer:
The calculations for Square (i) are shown below:
Adding along the rows:
Row 1:
Sum of the numbers = 5 + (–1) + (–4) = 5 – 1 – 4 = 0
Row 2:
Sum of the numbers = (–5) + (–2) + 7 = – 5 – 2 + 7 = 0
Row 3:
Sum of the numbers = 0 + 3 + (–3) = 3 – 3 = 0
Adding along the columns:
Column 1:
Sum of the numbers = 5 + (–5) + 0 = 5 – 5 = 0
Column 2:
Sum of the numbers = (–1) + (–2) + 3 = 0
Column 3:
Sum of the numbers = (–4) + 7 + (–3) = –4 + 7 – 3 = 0
Adding along the two diagonals:
5 + (–2) + (–3) = 5 – 2 – 3 = 0
(–4) + (–2) + 0 = – 4 – 2 = –6
Since the sum of the numbers in one diagonal = –6 and the remaining sums are all = 0, we conclude that Square (i) is not a magic square.
The calculations for Square (ii) are shown below:
Adding along the rows:
Row 1:
Sum of the numbers = 1 + (–10) + 0 = –9
Row 2:
Sum of the numbers = (–4) + (–3) + (–2) = –9
Row 3:
Sum of the numbers = (–6) + 4 + (–7) = –9
Adding along the columns:
Column 1:
Sum of the numbers = 1 + (–4) + (–6) = –9
Column 2:
Sum of the numbers = (–10) + (–3) + 4 = –9
Column 3:
Sum of the numbers = 0 + (–2) + (–7) = –9
Adding along the two diagonals:
1 + (–3) + (–7) = –9
0 + (–3) + (–6) = –9
Since, the sum of the number in all 3 rows, all 3 columns and both diagonals are all = –9, we conclude that Square (ii) is a magic square.
8. Verify a – (– b) = a + b for the following values of a and b.
(i) a = 21, b = 18
Ans:
LHS: a – (– b) = 21 – (– 18) = 21 + 18 = 39
RHS: a + b = 21 + 18 = 39
LHS = RHS, therefore, we can say it is verified.
(ii) a = 118, b = 125
Ans:
LHS: a – (– b) = 118 – (– 125) = 118 + 125 = 243
RHS: a + b = 118 + 125 = 243
LHS = RHS, therefore, we can say it is verified.
(iii) a = 75, b = 84
LHS: a – (– b) = 75 – (– 84) = 75 + 84 = 159
RHS: a + b = 75 + 84 = 159
LHS = RHS, therefore, we can say it is verified.
(iv) a = 28, b = 11
LHS: a – (– b) = 28 – (– 11) = 28 + 11 = 39
RHS: a + b = 28 + 11 = 39
LHS = RHS, therefore, we can say it is verified.
9. Use the sign of >, < or = in the box to make the statements true.
(a) (-8) + (-4) [ ] (-8) – (-4)
Answer:
LHS: (-8) + (-4) = – 8 – 4 = – 12
RHS: (-8) – (-4) = – 8 + 4 = – 4
– 12 < – 4 therefore, (-8) + (-4) [ < ] (-8) – (-4)
(b) (-3) + 7 – (19) [ ] 15 – 8 + (-9)
Answer:
LHS: (-3) + 7 – (19)=– 3 + 7 – 19 = – 15
RHS: 15 – 8 + (-9) = 15 – 8 – 9 = – 2
– 15 < – 2 therefore, (-3) + 7 – (19) [ < ] 15 – 8 + (-9)
(c) 23 – 41 + 11 [ ] 23 – 41 – 11
Answer:
LHS: 23 – 41 + 11 = – 7
RHS: 23 – 41 – 11 = – 29
– 7 > – 29 therefore, 23 – 41 + 11 [ > ] 23 – 41 – 11
(d) 39 + (-24) – (15) [ ] 36 + (-52) – (- 36)
Answer:
LHS: 39 + (-24) – (15) = 39 – 24 – 15 = 0
RHS: 36 + (-52) – (-36) = 36 – 52 + 36 = 20
0 < 20 therefore, 39 + (-24) – (15) [ < ] 36 + (-52) – (- 36)
(e) – 231 + 79 + 51 [ ] -399 + 159 + 81
Ans:
LHS: – 231 + 79 + 51 = – 101
RHS: -399 + 159 + 81 = – 159
– 101 > – 159 therefore, – 231 + 79 + 51 [ > ] -399 + 159 + 81
10. A water tank has steps inside it. A monkey is sitting on the topmost step (i.e., the first step). The water level is at the ninth step.

(i) He jumps 3 steps down and then jumps back 2 steps up. In how many jumps will he reach the water level?
Answer: Please refer to the figure below:
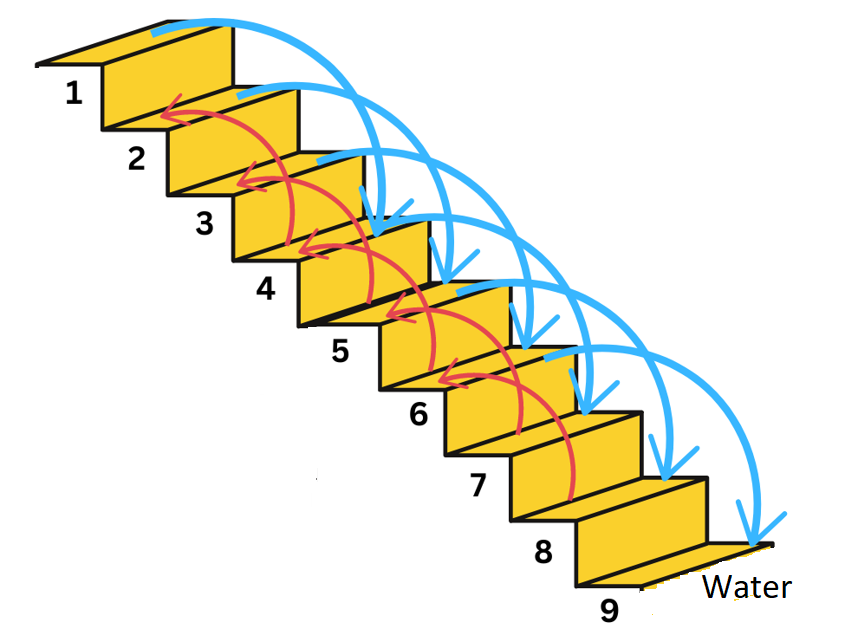
Let us assume that the number of steps jumped downward are represented by positive integers and the number of steps jumped upward are represented by negative integers.
The monkey jumps 3 steps down and 2 steps up.
Please refer to the figure along with the solution.
The monkey starts its journey from Step 1.
After the 1st jump, the monkey is at Step no = 1 + 3 = Step 4.
After the 2nd jump, the monkey is at Step no = 4 + (–2) = 4 – 2 = Step 2.
After the 3rd jump, the monkey is at Step no = 2 + 3 = Step 5.
After the 4th jump, the monkey is at Step no = 5 + (–2) = 5 – 2 = Step 3.
After the 5th jump, the monkey is at Step no = 3 + 3 = Step 6.
After the 6th jump, the monkey is at Step no = 6 + (–2) = 6 – 2 = Step 4.
After the 7th jump, the monkey is at Step no = 4 + 3 = Step 7.
After the 8th jump, the monkey is at Step no = 7 + (–2) = 7 – 2 = Step 5.
After the 9th jump, the monkey is at Step no = 5 + 3 = Step 8.
After 10th jump, the monkey is at Step no = 8 + (–2) = 8 – 2 = Step 6.
After 11th jump, the monkey is at Step no = 6 + 3 = Step 9.
Therefore, we conclude that the monkey took 11 jumps to each the water level.
(ii) After drinking water, he wants to go back. For this, he jumps 4 steps up and then jumps back 2 steps down with every move. In how many jumps will he reach back to the top step?
Answer:
Please refer to the figure below:
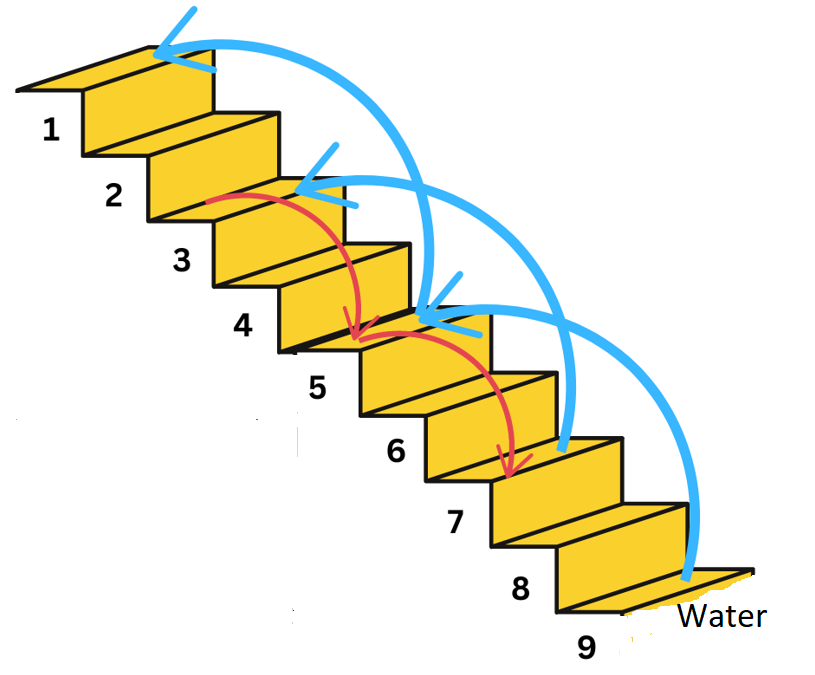
Let us assume that the number of steps jumped downward are represented by positive integers and the number of steps jumped upward are represented by negative integers.
The monkey jumps 4 steps up and 2 steps down.
Please refer to the figure along with the solution.
The monkey starts its journey from Step 9.
After the 1st jump, the monkey is at Step no = 9 + (–4) = 5 = Step 5
After the 2nd jump, the monkey is at Step no = 5 + 2 = Step 7.
After the 3rd jump, the monkey is at Step no = 7 + (–4) = Step 3.
After the 4th jump, the monkey is at Step no = 3 + 2 = 5 = Step 5.
After the 5th jump, the monkey is at Step no = 5 + (–4) = Step 1.
Therefore, we conclude that the monkey took 5 jumps to reach the top step.
(iii) If the number of steps moved down is represented by negative integers, and the number of steps moved up by positive integers, represent his moves in parts (i) and (ii) by completing the following: (a) – 3 + 2 – … = – 8 (b) 4 – 2 + … = 8. In (a), the sum (– 8) represents going down by eight steps. So, what will the sum 8 in (b) represent?
Answer:
It is given that number of steps moved down is represented by negative integers, and the number of steps moved up by positive integers.
(a) – 3 + 2 – … = – 8
In part (i) the monkey alternately jumps 3 steps down and 2 steps up.
By repeating the pattern, we get:
– 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 = – 18 + 10 = – 8.
(b) 4 – 2 + … = 8
In part (ii) the monkey alternately jumps 4 steps up and 2 steps down.
By repeating the pattern, we get:
4 – 2 + 4 – 2 + 4 = 12 – 4 = 8.
In (a), the sum (– 8) represents going down by eight steps. Therefore, the sum 8 in (b) represents going up by 8 steps.
Solutions to Exercise 1.2 (Page No 14) of NCERT Class 7 Math Chapter 1 Integers –
1. Find each of the following products:
(a) 3 × (–1)
Answer:
While multiplying a positive integer and a negative integer, we multiply them as whole numbers and put a minus (–) before the product.
For two positive integers a and b we can say, a × (–b) = (–a) × b = –(a × b).
Therefore, 3 × (–1) = –(3 × 1) = –3.
(b) (–1) × 225
Answer:
While multiplying a negative integer and a positive integer, we multiply them as whole numbers and put a minus (–) before the product.
For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b).
Therefore, (–1) × 225 = –(1 × 225) = –225.
(c) (–21) × (–30)
Answer:
The product of two negative integers is a positive integer. We multiply the two negative integers as whole numbers and put the positive sign before the product.
For two positive integers a and b, (–a) × (–b) = a × b.
Therefore, (–21) × (–30) = +21 × 30 = 630.
(d) (–316) × (–1)
Answer:
The product of two negative integers is a positive integer. We multiply the two negative integers as whole numbers and put the positive sign before the product.
For two positive integers a and b, (–a) × (–b) = a × b.
Therefore, (–316) × (–1) = +316 × 1 = 316.
(e) (–15) × 0 × (–18)
Answer:
Using commutative property of multiplication,
(–15) × 0 × (–18) = (–15) × (–18) × 0
(–15) × (–18) × 0 = (15 × 18) × 0 [For two positive integers a and b, (–a) × (–b) = a × b]
= 270 × 0
For any integer a,
a × 0 = 0 × a = 0
Therefore, 270 × 0 = 0.
(f) (–12) × (–11) × (10)
Answer:
For two positive integers a and b, (–a) × (–b) = a × b.
So, (–12) × (–11) = 132
Therefore, (–12) × (–11) × (10) = 132 × 10 = 1320.
(g) 9 × (–3) × (– 6)
Answer:
(–3) × (– 6) = 18 [For two positive integers a and b, (–a) × (–b) = a × b]
9 × (–3) × (– 6) = 9 × 18 = 162
(h) (–18) × (–5) × (– 4)
Answer:
(–18) × (–5) × (– 4)
= [(–18) × (–5)] × (– 4)
= (18 × 5) × (– 4) [For two positive integers a and b, (–a) × (–b) = a × b]
= 90 × (– 4)
= – (90 × 4) [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= – 360
(i) (–1) × (–2) × (–3) × 4
Answer:
We take the first 3 integers first:
(–1) × (–2) × (–3)
= [(–1) × (–2)] × (–3)
= (1 × 2) × (–3) [For two positive integers a and b, (–a) × (–b) = a × b]
= 2 × (–3)
= – (2 × 3) [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= – 6
Therefore, (–1) × (–2) × (–3) × 4 = – 6 × 4 = – 24
(j) (–3) × (–6) × (–2) × (–1)
Answer:
If the number of negative integers in a product is even, then the product is a positive integer.
(–3) × (–6) × (–2) × (–1) = +(3 × 6 × 2 × 1) = 36
2. Verify the following:
(a) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]
Answer:
LHS: 18 × [7 + (–3)] = 18 × (7 – 3) = 18 × 4 = 72
RHS: [18 × 7] + [18 × (–3)]
= 126 + [–(18 × 3)] [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= 126 – 54 = 72
Therefore, LHS = RHS and it is verified.
(b) (–21) × [(– 4) + (– 6)] = [(–21) × (– 4)] + [(–21) × (– 6)]
Answer:
LHS: (–21) × [(– 4) + (– 6)]
= (–21) × (– 4 – 6)
= (–21) × (– 10)
= 21 × 10 [For two positive integers a and b, (–a) × (–b) = a × b]
= 210
RHS: [(–21) × (– 4)] + [(–21) × (– 6)]
= (21 × 4) + (21 × 6) [For two positive integers a and b, (–a) × (–b) = a × b]
= 210
Therefore, LHS = RHS and it is verified.
3. (i) For any integer a, what is (–1) × a equal to?
Answer:
We can see that:
(–1) × a
= – (1 × a) [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= –a
We get the additive inverse (–a) of the integer a when we multiply (–1) to a.
(ii) Determine the integer whose product with (–1) is
(a) –22
Answer:
We can see that:
(–1) × a
= – (1 × a) [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= –a
Therefore, we can see that,
(–1) × 22 = – 22
So, the integer whose product with (–1) gives –22 = 22
We get the additive inverse 22 of the integer –22 when we multiply (–1) to –22.
(b) 37
Answer:
We can see that:
(–1) × a
= – (1 × a) [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
= –a
Therefore, we can see that,
(–1) × (–37) = 37
So, the integer whose product with (–1) gives –37 = 37
(c) 0
Answer:
For any integer a,
a × 0 = 0 × a = 0
We can see that, (–1) × 0 = 0.
Therefore, the integer whose product with (–1) gives 0 is 0.
4. Starting from (–1) × 5, write various products showing some pattern to show (–1) × (–1) = 1.
Answer:
The various products are shown below,
= –1 × 5 = –5
= –1 × 4 = –4
= –1 × 3 = –3
= –1 × 2 = –2
= –1 × 1 = –1
= –1 × 0 = 0
Recognising the pattern above, we can say that:
(–1) × (–1) = 1
5. Find the product using suitable properties:
(a) 26 × (–48) + (–48) × (–36)
Answer:
Using the property that multiplication is commutative for integers, we get:
26 × (–48) + (–48) × (–36)
= (–48) × 26 + (–48) × (–36)
Using the property of distributivity of multiplication over addition:
In general, for any integers a, b and c,
a × (b + c) = a × b + a × c
Therefore, (–48) × 26 + (– 48) × (–36)
= (–48) × [26 + (–36)]
= (–48) × (26 – 36)
= (–48) × (–10)
= 480 [For two positive integers a and b, (–a) × (–b) = a × b]
(b) 8 × 53 × (–125)
Answer:
Using the commutative property of multiplication:
8 × 53 × (–125) = 8 × (–125) × 53
= [8 × (–125)] × 53
= 1000 × 53
= 53000
(c) 15 × (–25) × (– 4) × (–10)
Answer:
We proceed to make the multiplication easy to solve:
Using the commutative property of multiplication, we get:
15 × (–25) × (– 4) × (–10)
= 15 × (–25) × (–10) × (– 4)
Using the commutative property of multiplication for the second time, we get:
15 × (–25) × (–10) × (– 4)
= [15 × (–10)] × [(–25) × (– 4)]
For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
Also, for two positive integers a and b, (–a) × (–b) = a × b
Therefore, [15 × (–10)] × [(–25) × (– 4)]
= (–150) × (100)
= –15000 [(–a) × b = a × (–b) = –(a × b)]
(d) (–41) × 102
Answer:
Using the property of distributivity of multiplication over addition:
In general, for any integers a, b and c,
a × (b + c) = a × b + a × c
(–41) × 102
= (–41) × (100 + 2)
= (–41) × 100 + (–41) × 2
= –41 × 100 – 41 × 2
= –4100 – 82
= –4182
(e) 625 × (–35) + (– 625) × 65
Answer:
625 × (–35) + (–625) × 65
= 625 × (–35) + 625 × (–65) [For two positive integers a and b we can say, (–a) × b = a × (–b)]
= 625 × (–35 – 65)
= 625 × (–100)
= – 62500 [For two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)]
(f) 7 × (50 – 2)
Answer:
Using the property of distributivity of multiplication over subtraction:
In general, for any integers a, b and c,
a × (b – c) = a × b – a × c
Therefore,
7 × (50 – 2)
= 7 × 50 – 7 × 2
= 350 – 14
= 336
(g) (–17) × (–29)
Answer:
(–17) × (–29)
= (–17) × (–30 + 1)
Using the property of distributivity of multiplication over addition:
In general, for any integers a, b and c,
a × (b + c) = a × b + a × c
Therefore,
(–17) × (–30 + 1)
= (–17) × (–30) + (–17) × 1
For two positive integers a and b, (–a) × (–b) = a × b.
Also, for two positive integers a and b we can say, (–a) × b = a × (–b) = –(a × b)].
Therefore,
(–17) × (–30) + (–17) × 1
= (17 × 30) – (17 × 1)
= 510 – 17
= 510 – 17
= 493
(h) (–57) × (–19) + 57
Answer:
For two positive integers a and b, (–a) × (–b) = a × b.
So,
(–57) × (–19) + 57
= 57 × 19 + 57
= 57 × 19 + 57 × 1
Using the property of distributivity of multiplication over addition:
In general, for any integers a, b and c,
a × (b + c) = a × b + a × c
So,
57 × 19 + 57 × 1
= 57 × (19 + 1)
= 57 × 20
= 1140
6. A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5°C every hour. What will be the room temperature 10 hours after the process begins?
Answer:
The initial room temperature = 40°C.
It will be lowered at the rate of 5°C every hour.
Let us represent the lowering of the temperature by a negative number.
Therefore, the rate of temperature change = –5°Cper hour.
Therefore, 10 hours after the process begins the total temperature change = (–5°Cper hour) × 10 hours = –50°C.
Therefore, the final room temperature = 40°C – 50°C = –10°C.
7. In a class test containing 10 questions, 5 marks are awarded for every correct answer and (–2) marks are awarded for every incorrect answer and 0 for questions not attempted.
(i) Mohan gets four correct and six incorrect answers. What is his score?
Answer:
5 marks are awarded for every correct answer.
Mohan gets four correct answers.
Therefore, total marks awarded for correct answers = 5 × 4 = 20 marks.
(–2) marks are awarded for every incorrect answer.
Therefore, total marks awarded for correct answers = 6 × (–2) = –12 marks.
Therefore, total marks = 20 + (–12) = 20 – 12 = 8 marks.
(ii) Reshma gets five correct answers and five incorrect answers; what is her score?
Answer:
5 marks are awarded for every correct answer.
Reshma gets five correct answers.
Therefore, total marks awarded for correct answers = 5 × 5 = 25 marks.
(–2) marks are awarded for every incorrect answer.
Reshma gets five incorrect answers.
Therefore, total marks awarded for incorrect answers = 5 × (–2) = –10 marks.
Therefore, total marks = 25 + (–10) = 25 – 10 = 15 marks.
(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
Answer:
5 marks are awarded for every correct answer.
Heena gets two correct answers.
Therefore, total marks awarded for correct answers = 5 × 2 = 10 marks.
(–2) marks are awarded for every incorrect answer.
Heena gets five incorrect answers.
Therefore, total marks awarded for incorrect answers = 5 × (–2) = –10 marks.
Therefore, total marks = 10 + (–10) = 0 marks.
8. A cement company earns a profit of ₹ 8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold.
(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?
Answer:
Let us represent profit in integers numbers and loss in negative integers.
A cement company earns a profit of ₹ 8 per bag.
The company sells 3,000 bags of white cement.
Therefore, the total profit = 3000 × ₹ 8 = ₹ 24000.
The companysells 5,000 bags of grey cement in a month.
Loss per bag of grey cement sold = –₹ 5.
Therefore, the total loss = 5000 × (–₹ 5) = –₹ 25000.
Therefore, the total profit or loss can be found as = ₹ 24000 + (–₹ 25000) = –₹ 1000.
Since –₹ 1000 is a negative number, we conclude that there a loss of ₹ 1000.
(b) What is the number of white cement bags it must sell to have neither profit nor loss, if the number of grey bags sold is 6,400 bags?
Answer:
Let us represent profit in integers numbers and loss in negative integers.
Loss per bag of grey cement sold = –₹ 5.
Therefore, the total loss = 6400 × (–₹ 5) = –₹ 32000.
Therefore, to have neither profit nor loss:
Total profit + total loss = 0.
Total profit + (–₹ 32000) = 0
Therefore, total profit = ₹ 32000.
Profit per bag of white cement = ₹ 8.
Therefore, number of white cement bags it must sell to have neither profit nor loss = = 4000.
9. Replace the blank with an integer to make it a true statement.
(a) (–3) × _____ = 27
Answer:
(–3) × _____ = 27
or, (–3) × _____ = 3 × 9
Therefore we get,
(–3) × (–9) = 3 × 9 [For two positive integers a and b, (–a) × (–b) = a × b]
or, (–3) × (–9) = 27
(b) 5 × _____ = –35
Ans:
5 × _____ = –35
or, 5 × _____ = –(5 × 7)
Therefore we get,
5 × (–7) = –(5 × 7) [For two positive integers a and b we can say, a × (–b) = –(a × b)]
or, 5 × (–7) = –35
(c) _____ × (– 8) = –56
Ans:
_____ × (– 8) = –56
or, _____ × (– 8) = –(7 × 8)
Therefore we get,
(7) × (– 8) = –(7 × 8) [For two positive integers a and b we can say, a × (–b) = –(a × b)]
or, (7) × (– 8) = –(56)
(d) _____ × (–12) = 132
Ans:
_____ × (–12) = 132
or, _____ × (–12) = 11 × 12
Therefore we get,
(–11) × (–12) = 11 × 12 [For two positive integers a and b, (–a) × (–b) = a × b]
or, (–11) × (–12) = 132
Solutions to Exercise 1.3 (Page No 18) of NCERT Class 7 Math Chapter 1 Integers –
1. Evaluate each of the following.
(a) (–30) ÷ 10
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, (–30) ÷ 10 = –3
(b) 50 ÷ (–5)
Answer:
When we divide a positive integer by a negative integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, 50 ÷ (–5) = –10
(c) (–36) ÷ (–9)
Answer:
When we divide a negative number by a negative number, we first divide them as whole numbers and positive sign (+). In general, for any two positive integers a and b, (–a) ÷ (–b) = a ÷ b where b ≠ 0.
So, (–36) ÷ (–9) = 4
(d) (–49) ÷ (49)
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, (–49) ÷ 49 = –1
(e) 13 ÷ [(–2) + 1]
Answer:
13 ÷ [(–2) + 1]
= 13 ÷ (–1)
When we divide a positive integer by a negative integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, 13 ÷ (–1) = –13
(f) 0 ÷ (–12)
Answer:
Zero divided by an integer other than zero is equal to zero. For any integer a ≠ 0, 0 ÷ a = 0.
Therefore, 0 ÷ (–12) = 0.
(g) (–31) ÷ [(–30) + (–1)]
Answer:
(–31) ÷ [(–30) + (–1)]
= (–31) ÷ (–30 –1)
= (–31) ÷ (–31)
When we divide a negative number by a negative number, we first divide them as whole numbers and positive sign (+). In general, for any two positive integers a and b, (–a) ÷ (–b) = a ÷ b where b ≠ 0.
(–31) ÷ (–31) = 1
(h) [(–36) ÷ 12] ÷ 3
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
The division in the bracket must be carried out first.
Therefore, (–36) ÷ 12 = –3
Then we get, –3 ÷ 3 = –1
(i) [(– 6) + 5)] ÷ [(–2) + 1]
Answer:
The operations within the brackets must be carried out first.
[(–6) + 5)] ÷ [(–2) + 1]
= (–1) ÷ (–1)
h
(–1) ÷ (–1) = 1
2. Verify that a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c) for each of the following values of a, b and c.
(a) a = 12, b = –4, c = 2
Answer:
LHS:
a ÷ (b + c)
= 12 ÷ (–4 + 2)
= 12 ÷ (–2)
When we divide a positive integer by a negative integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, 12 ÷ (–2) = –6
LHS = –6
RHS:
(a ÷ b) + (a ÷ c)
= [12 ÷ (–4)] + [12 ÷ 2]
= –3 + 6
= 3
RHS = 3
Since –6 ≠ 3, it is proved that LHS ≠ RHS.
(b) a = (–10), b = 1, c = 1
Answer:
LHS:
a ÷ (b + c)
= (–10) ÷ (1 + 1)
= (–10) ÷ 2
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
So, (–10) ÷ 2 = –5
LHS = –5
RHS:
(a ÷ b) + (a ÷ c)
[(–10) ÷ 1] + [(–10) ÷ 1]
= (–10) + (–10)
= –10 – 10
= –20
RHS = –20
Since –5 ≠ –20 it is proved that LHS ≠ RHS.
3. Fill in the blanks:
(a) 369 ÷ _____ = 369
Answer:
Any integer divided by 1 gives the same integer.
Therefore, 369 ÷ 1 = 369.
(b) (–75) ÷ _____ = –1
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
Therefore, (–75) ÷ 75 = –1
(c) (–206) ÷ _____ = 1
Answer:
When we divide a negative number by a negative number, we first divide them as whole numbers and positive sign (+). In general, for any two positive integers a and b, (–a) ÷ (–b) = a ÷ b where b ≠ 0.
Therefore, (–206) ÷ (–206) = 1
(d) –87 ÷ _____ = 87
Answer:
When we divide a negative number by a negative number, we first divide them as whole numbers and positive sign (+). In general, for any two positive integers a and b, (–a) ÷ (–b) = a ÷ b where b ≠ 0.
Therefore, –87 ÷ (–1) = 87
(e) _____ ÷ 1 = – 87
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
Therefore, (– 87) ÷ 1 = – 87
(f) _____ ÷ 48 = –1
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
Therefore, (– 48) ÷ 48 = –1
(g) 20 ÷ _____ = –2
Answer:
When we divide a positive integer by a negative integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
Therefore, 20 ÷ (–10) = –2
(h) _____ ÷ (4) = –3
Answer:
When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
Therefore, (–12) ÷ (4) = –3.
4. Write five pairs of integers (a, b) such that a ÷ b = –3. One such pair is (6, –2) because 6 ÷ (–2) = (–3).
Answer:
When we divide a positive integer by a negative integer, we divide them as whole numbers and then put a minus sign (–) before the quotient.
The five pairs of integers are as follows:
(i) (9, –3)
We can see that, 9 ÷ (–3) = –3.
(ii) (–9, 3)
We can see that, (–9) ÷ 3 = –3.
(iii) (12, –4)
We can see that, 12 ÷ (–4) = –3.
(iv) (–12, 4)
We can see that, (–12) ÷ 4 = –3.
(v) (15, –5)
We can see that, 15 ÷ (–5) = –3.
5. The temperature at 12 noon was 10o C above zero. If it decreases at the rate of 2o C per hour until midnight, at what time would the temperature be 8°C below zero? What would be the temperature at mid-night?
Answer:
The temperature at 12 noon = 10o C.
Rate of change of temperature = –2o C per hour (The temperature is decreasing, so it is represented by a negative number).
We are required to find the time when the temperature = –8°C.
We find,
At 1 pm, temperature = 10o C + (–2o C) = 10o C – 2o C = 8o C.
At 2 pm, temperature = 8o C + (–2o C) = 8o C – 2o C = 6o C.
At 3 pm, temperature = 6o C + (–2o C) = 6o C – 2o C = 4o C.
At 4 pm, temperature = 4o C + (–2o C) = 4o C – 2o C = 2o C.
At 5 pm, temperature = 2o C + (–2o C) = 2o C – 2o C = 0o C.
At 6 pm, temperature = 0o C + (–2o C) = 0o C – 2o C = –2o C.
At 7 pm, temperature = –2o C + (–2o C) = –2o C – 2o C = –4o C.
At 8 pm, temperature = –4o C + (–2o C) = –4o C – 2o C = –6o C.
At 9 pm, temperature = –6o C + (–2o C) = –6o C – 2o C = –8o C.
Therefore, the temperature will be 8°C below zero (–8o C) at 9 pm.
The temperature at mid-night (12 am) can be found as follows:
From 12 noon to 12 am, the gap is 12 hours.
Rate of change of temperature = –2o C per hour.
Therefore, the total change of temperature in 12 hours = –2o C per hour × 12 hours = –24 o C.
The temperature at 12 noon = 10o C.
Therefore, the temperature at mid-night = 10o C – 24o C = –14o C or 14o C below 0.
6. In a class test, (+ 3) marks are given for every correct answer and (–2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
Answer:
Radhika scored 20 marks.
Number of correct answers she has got = 12.
Marks given for every correct answer = 3.
Therefore, total number of marks given for 12 correct answers = 12 × 3 = 36.
The total number of marks awarded for incorrect answers = Total number of marks – total number of marks awarded for correct answers.
Therefore, total number of marks awarded for incorrect answers = 20 – 36 = –16.
The marks awarded for every correct answer is represented by a positive integer, therefore the marks awarded for every incorrect answer is represented by a negative integer.
Marks given for every incorrect answer = –2.
Therefore, the total number of questions she attempted incorrectly = (–16) ÷ (–2) = 8.
(ii) Mohini scores –5 marks in this test, though she got 7 correct answers. How many questions has she attempted incorrectly?
Answer:
Total marks Mohini scores = –5 marks.
Number of correct answers she has got = 7.
Marks given for every correct answer = 3.
Therefore, total number of marks given for 7 correct answers = 7 × 3 = 21.
The total number of marks awarded for incorrect answers = Total number of marks – total number of marks awarded for correct answers.
Therefore, total number of marks awarded for incorrect answers = –5 – 21 = –26.
Marks given for every incorrect answer = –2.
Therefore, the total number of questions she attempted incorrectly = (–26) ÷ (–2) = 13.
7. An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m?
Answer:
The initial height above the ground level = 10 m.
The final depth below the ground level = –350 m.
The total distance descended by the elevator = –350 m – 10 m = –360 m.
The rate of descent will be represented by a negative number.
Therefore, the elevator descends into a mine shaft at the rate of –6 m/min.
Therefore, the total time taken = (–360 m ÷ –6 m/min) = 60 min.
Important Questions from Previous NCERT Textbook:
Exercise 1.2 Page No: 9 (Old Textbook):
1. Write down a pair of integers whose:
(a) sum is -7
Answer:
We can see that:
(–1) + (–6) = – 1 – 6 = – 7.
Therefore, the pair of integers are – 1, – 6.
(b) the difference is – 10
Answer:
We can see that:
(–12) – (–2) = –12 + 2 = –10 [For subtraction, we add the additive inverse of the integer that is being subtracted to the other integer. Therefore, a – (-b) = a + additive inverse of (-b) = a + b]
Therefore, the pair of integers are –12, –2.
(c) sum is 0
Answer:
We can see that:
5 + (–5) = 5 – 5 = 0
Therefore, the pair of integers are 5, –5.
2. (a) Write a pair of negative integers whose difference gives 8.
Answer:
We can see that:
–2 – (–10) = –2 + 10 = 8 [For subtraction, we add the additive inverse of the integer that is being subtracted to the other integer. Therefore, a – (-b) = a + additive inverse of (-b) = a + b]
Therefore, the pair of negative integers whose difference gives 8 = –2, –10.
(b) Write a negative integer and a positive integer whose sum is – 5.
Answer:
We can see that:
–7 + 2 = – 5
Therefore, the negative integer can be –7 and the positive integer can be 2.
(c) Write a negative integer and a positive integer whose difference is – 3.
Answer:
We can see that:
–1 – 2 = –3
Therefore, the negative integer can be –1 and the positive integer is 2.
3. In a quiz, team A scored – 40, 10, 0 and team B scored 10, 0, – 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
Answer:
The scores of team A are: – 40, 10, 0.
The scores of team B are: 10, 0, – 40.
The total scores of team A = – 40 + 10 + 0 = – 30.
The total scores of team B = 10 + 0 + (– 40) = 10 – 40 = – 30.
The scores of both teams are the same.
Yes, the integers can be added in any order (as is evident from the two additions above).
4. Fill in the blanks to make the following statements true.
(i) (–5) + (– 8) = (– 8) + (…………)
Answer:
Using the commutative property of addition of integers, we can say:
For any integers a and b, a + b = b + a
Therefore, (–5) + (– 8) = (– 8) + (–5).
(ii) –53 + ………… = –53
Answer:
Zero is an additive identity for integers.
Therefore, –53 + 0 = –53
(iii) 17 + ………… = 0
Answer:
17 + (–17) = 0 [– 17 is the additive inverse of 17)
(iv) [13 + (– 12)] + (…………) = 13 + [(–12) + (–7)]
Answer:
Using the associative property for addition of integers, we can say:
(a + b) + c = a + (b + c)
Therefore, [13 + (– 12)] + (–7) = 13 + [(–12) + (–7)]
(v) (– 4) + [15 + (–3)] = [– 4 + 15] +…………
Answer:
Using the associative property for addition of integers, we can say:
a + (b + c) = (a + b) + c
Therefore, (– 4) + [15 + (–3)] = [– 4 + 15] + (–3)
Extra Questions to Complement Solutions to NCERT Class 7 Mathematics Chapter 1 Integers:
(A) Very Short Answer Type Questions:
1. How many pairs of integers can you find whose difference is 2?
Answer:
You can find infinite pairs of integers whose difference is 2.
2. How many pairs of integers can you find whose sum is 0?
Answer:
You can find infinite pairs of integers whose sum is 0.
3. Write a pair of integers whose sum gives an integer smaller than both the integers.
Answer:
The pair of integers can be – 2, – 3. Their sum = – 2 – 3 = – 5 which is smaller than both –2 and – 3.
4. What number do we multiply 5 with to get the additive inverse of 5?
Answer:
We multiply the number by – 1 to get the additive inverse. We see that 5 × (– 1) = – 5.
5. What property would you use to express 6 × (4 + 2) as the sum of two multiplications?
Answer:
Distributive property. Using distributive property, we get 6 × (4 + 2)= 6 × 4 + 6 × 2.
6. If we add a positive integer and a negative integer, what do we get?
Answer:
If the positive integer is greater than the negative integer, we get a positive sum. If the positive integer is lesser than the negative integer, we get a negative sum.
7. What do you get when you add -1 to the integer lying to the right of -1 on the number line?
Answer:
The integer lying to the right of -1 on the number line is 0. Adding -1 to 0 we get the sum as (-1 + 0) = -1, which is the number -1 again.
8. Which one of the four basic mathematical operations is not closed?
Answer:
Division is not closed.
9. For which value of b is the division a ÷ b not possible?
Answer:
a ÷ b is not possible for b = 0.
10. The value of 20 ÷ (-2) × (-3) lies to which side of zero?
Answer:
20 ÷ (-2) × (-3) = (-10) × (-3) = 30.
30 lies to the right of 0 on the number line.
(B) Multiple Choice Questions (MCQ):
1. If we subtract the number 3 five times from 30 what do we get?
(a) 12
(b) 15
(c) 18
(d) 21
Answer: (b) 15
30 – 3 × 5 = 30 – 15 = 15
2. Write the next digit in the following pattern: -9, -3, 3, 9, 15, _______.
(a) 21
(b) 22
(c) 18
(d) 27
Answer:(a) 21
We have,
-3 – (-9) = – 3 + 9 = 6
3 – (-3) = 3 + 3 = 6
9 – 3 = 6
Therefore, the difference between consecutive number is 6.
Therefore, the next digit in the pattern = 15 + 6 = 21.
3. Evaluate (-10) × (-12) × (-6) × (-10).
(a) 7200
(b) -7200
(c) 1200
(d) -1200
Answer:
We have, (-10) × (-12) × (-6) × (-10)
= (10 × 12) + (6 × 10) [Using (– a) × (– b) = a × b]
= 120 + 60
= 180 (Answer)
4. Which one of the following is not equal to (-a) × b?
(a) -(ab)
(b) -1 × a × b
(c) -b × a
(a) (-a) × (-b)
Answer: (a) (-a) × (-b)
5. Which property of addition does not hold for division?
(a) Commutativity
(b) Associativity
(c) Commutativity and Associativity
(d) All properties for addition hold for division
Answer: (c) Commutativity and Associativity
(C) Short and Long Answer Type Questions:
1. Show using the digits 4 and 6 that:
(i) Addition is commutative (ii) Subtraction is not commutative
Answer:
(i) Addition is commutative
We have:
4 + 6 = 10 and 6 + 4 = 10
So, 4 + 6 = 6 + 4
Therefore, we can see that addition is commutative.
(ii) Subtraction is not commutative
We have:
4 – 6 = – 2 and 6 – 4 = 2
Therefore, we can see that subtraction is not commutative.
2. Starting from (–5) × 4, find (–5) × (– 6)
Answer:
(–5) × 4 = -20
(–5) × 3 = -15 = -20 – (-5)
(–5) × 2 = -10 = -15 – (-5)
(–5) × 1 = -5 = -10 – (-5)
(-5) × 0 = 0 = -5 – (-5)
(-5) × (-1) = 5 = 0 – (-5) = 0 + 5 = 5
(-5) × (-2) = 10 = 5 – (-5) = 5 + 5 = 10
Based on the above pattern we get,
(–5) × (– 6) = 30 (Answer)
3. Express 30 as 5 multiplied by the sum of two even numbers:
Answer:
30 = 5 × 6
6 can be written as:
6 = 5 + 1
6 = 4 + 2
6 = 3 + 3
The sum of two even numbers would be (4 + 2).
Therefore, we can write 30 = 5 × (4 + 2). (Answer)
4. Using appropriate properties evaluate:
(i) 6 × (3 + 2) + 5 × (8 – 2) (ii) (5 – 6) × 2 + (4 – 1) × 5
Answer:
(i) 6 × (3 + 2) + 5 × (8 – 2)
Using distributive property we get:
6 × (3 + 2) + 5 × (8 – 2)
= 6 × 3 + 6 × 2 + 5 × 8 – 5 × 2
= 18 + 12 + 40 – 10
= 60 (Answer)
(ii) (5 – 6) × 2 + (4 – 1) × 5
(5 – 6) × 2 + (4 – 1) × 5
= 2 × (5 – 6) + 5 × (4 – 1) [Using commutative property]
= 2 × 5 – 2 × 6 + 5 × 4 – 5 × 1 [Using distributive property]
= 10 – 12 + 20 – 5
= 13 (Answer)
5. Evaluate:
(i) 6 × 5 – 5 × 7 (ii) 3 × 6 – 7 × 4 + 6 × 5 – 4 × 5
Answers:
(i) 6 × 5 – 5 × 7
= 5 × 6 – 5 × 7 (Using commutative property)
= 5 × (6 – 7) (Using distributive property)
= 5 × (-1)
= -5 (Answer)
(ii) 3 × 6 – 7 × 4 + 6 × 5 – 4 × 5
= 3 × 6 + 6 × 5 – 7 × 4 – 4 × 5 (Rearrangement)
= 6 × 3 + 6 × 5 – 4 × 7 – 4 × 5 (Using commutative property)
= 6 × (3 + 5) – 4 × (7 + 5) (Using distributive property)
= 6 × 8 – 4 × 12
= 48 – 48
= 0 (Answer)
6. An air force transport plane which is 100 m above the ground descends vertically at the rate of 5 m/min. After 8 mins what would it be its height from the ground? How long more will take for the plane to reach the ground?
Answer:
Let the distance vertically upwards be positive and the distance vertically downwards be negative.
The height it covers in 8 mins = (-5 m/min × 8 min) = – 40 m.
Therefore, after 8 mins its height from the ground = 100 + (– 40) m = 60 m.
The amount of time taken by the plane to reach the ground = = 12 minutes.
7. How many integers lie between (-3) × 4 and 6 ÷ (-2)?
Answer:
We have (-3) × 4 =- 12 and 6 ÷ (-2) = -3.
Integers lying between -12 and -3 are -11, -10, -9, -8, -7, -6, -5, -4.
Therefore, the number of integers = 8. (Answer)
8. Each step is of a height of 10 cm. A person starts from the ground, climbs 8 steps and then descends 2 steps. What is his height above the ground.
Answer:
When a person climbs 8 steps his height above the ground = (10 cm × 8) = 80 cm.
When the person descends 2 steps the distance covered = (-10 cm × 2) = – 20 cm.
Therefore, his height above the ground = 80 cm + (-20 cm) = 80 cm – 20 cm = 60 cm.
9. Simplify the following:
(i) a × b + b × c – b × a + c × b (ii) a × b + b × c + c × (a + b)
where a, b and c are integers.
Answers:
(i) a × b + b × c – b × a + c × b
= a × b – b × a + b × c + c × b
= a × b – a × b + b × c + b × c (Using commutative property)
= 2 × b × c
(ii) a × b + b × c + c × (a + c)
= b × a + b × c + c × (a + c) (Using commutative property)
= b × (a + c) + c × (a + c)
Since a and c are integers, (a + c) is also an integer.
So, b × (a + c) + c × (a + c)
= (a + c) × b + (a + c) × c (Using commutative property)
= (a + c) × (b + c) (Using distributive property)
10. You are given that: a Δ b = – a. Find the value of:
(i) 6 Δ 3 (ii) -3 Δ -3
Answers:
(i) 6 Δ 3
Given: a Δ b = – a
Therefore, 6 Δ 3 = – 6 = 2 – 6 = -4 (Answer)
(ii) -3 Δ -3
Given: a Δ b = – a
Therefore, -3 Δ -3 = – (-3) = 1 + 3 = 4 (Answer)
(D) Fill in the Blanks:
(a) If we multiply three negative integers with one positive integer, the resulting number will be a _________ number.
(b) When we divide an integer with its additive inverse, we get the number _________.
(c) The product of an even and an odd integer is always _________.
(d) In the addition of three integers, any two integers can be added first and then the third. The statement is _________.
(e) If a is an integer then the value of 3 x a ÷ (-a) is _________ (-3).
Answers:
(a) If we multiply three negative integers with one positive integer, the resulting number will be a negative number
(b) When we divide an integer with its additive inverse, we get the number -1.
(c) The product of an even and an odd integer is always even.
(d) In the addition of three integers, any two integers can be added first and then the third. The statement is True.
(e) If a is an integer then the value of 3 x a ÷ (-a) is -3.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 7 Maths Chapter 1 Integers:
These solutions have been crafted with utmost care by Indian and foreign educated engineers and scientists in a scientific and logical manner, which will help your understanding. We understand that the readers are young and your needs are unique, and so we strive to give you the best possible learning experience. We have solved the questions in a way that complements the material in Chapter 1 of the Class 7 Maths NCERT textbook, so that it easy for you to follow along.
The PDF version of the solution is free for you to use and download! We do our best to ensure that we provide you with the best study material and we will provide you plenty more! So make sure you keep visiting our website and join our email list to stay updated!
The main topics covered are:
1.1 – Properties of Addition and Subtraction of Integers
1.2 – Multiplication of Integers
1.3 – Properties of Multiplication of Integers
1.4 – Division of Integers
1.5 – Properties of Division of Integers
Here are the number of problems by each chapter:
Exercise 1.1 – 4 questions
Exercise 1.2 – 4 questions
Exercise 1.3 – 7 questions
Yes, the PDFs of the solutions are available for you to download (please look towards the top of the page) for free!
The most important properties of the chapter are the properties of addition, subtraction, multiplication and division of integers. Learn them well and practise problems which require you to apply them. Our solutions materials and extra problems are designed to help you quickly grasp the concepts and be able to apply them. They are an excellent to start your practise.
Need extra coaching? Our amazing teacher-mentors will give their all to help you achieve success. Reach out to us anytime and let us help you out! (Insert hyperlink)
At educationroundtheworld.com, we care for your needs. Our expert teacher-mentors not only provide top-quality coaching, but also mentor students regarding their future careers. This helps in overall development and readies the students to face any challenge that lies ahead. So if you need us to teach you and mentor you, or if you have any feedback, reach out to us anytime! We provide tailored one-to-one coaching and mentoring services, based on your convenience and your needs – have it completely your way! Book an appointment now!


