Hello students – welcome to Class 8! Our Chapter 1 solutions are an excellent place to continue your study on rational numbers. The exercise solutions and extra problems have been designed and solved in a manner that will help clear your concepts. If you study them well, you will quickly learn to solve unknown problems by yourself.
Solutions to Exercise 1.1 (Page No 12) of NCERT Class 8 Math Chapter 1 Integers –
1. Name the property under multiplication used in each of the following.
(i) (-4)/5 × 1 = 1 × (-4)/5 = – 4/5
(ii) – 13/17 × (-2)/7 = (-2)/7 × (-13)/17
(iii) (-19)/29 × 29/(-19) = 1
Answers:
(i) (-4)/5 × 1 = 1 × (-4)/5 = – 4/5 uses the property that 1 is the multiplicative identity for rational numbers.
(ii) – 13/17 × (-2)/7 = (-2)/7 × (-13)/17 uses the property of associativity of multiplication of rational numbers.
(iii) (-19)/29 × 29/(-19) = 1 uses the property of multiplicative inverse for rational numbers.
Summary: (i) uses the property that 1 is the multiplicative identity for rational numbers, (ii) uses the property of associativity of multiplication of rational numbers and (iii) uses the property of multiplicative inverse for rational numbers.
2. Tell what property allows you to compute 1/3 × (6 × 4/3) as (1/3 × 6) × 4/3 .
Answer: The expression is of the form a × (b × c) = (a × b) × c, where a = 1/3 , b = 6 and c = 4/3 . Hence, the property used is associative property of multiplication.
3. The product of two rational numbers is always a __.
Answer: The product of two rational numbers is always a rational number.
Important Questions from Previous NCERT Textbook:
Exercise 1.1 Page No: 14 (Old Textbook):
1. Using appropriate properties find.
(i) – 2/3 × 3/5 + 5/2 – 3/5 × 1/6
Answer:
We have – 2/3 × 3/5 + 5/2 – 3/5 × 1/6
= (-2)/3 × 3/5 – 3/5 × 1/6 + 5/2 (By commutativity for addition)
= 3/5 × ((-2)/3) – 3/5 × 1/6 + 5/2 (By commutativity for multiplication)
= 3/5 × ((-2)/3 – 1/6) + 5/2 (Using distributivity property)
= 3/5 × ((-4 – 1)/6) + 5/2
= 3/5 × ((-5)/6) + 5/2
= (-1)/2 + 5/2
= 4/2
= 2 (Answer)
(ii) 2/5 × (– 3/7 ) – 1/6 × 3/2 + 1/14 × 2/5
Answer:
We have 2/5 × (– 3/7 ) – 1/6 × 3/2 + 1/14 × 2/5
= 2/5 × (– 3/7 ) + 1/14 × 2/5 – 1/6 × 3/2 (By commutativity for addition)
= 2/5 × (– 3/7 ) + 2/5 × 1/14 – 1/6 × 3/2 (By commutativity for multiplication)
= 2/5 × ((-3)/7 + 1/14) – 1/4 (Using distributivity of multiplication over addition)
= 2/5 × ((-6 + 1)/14) – 1/4
= 2/5 × ((-5 )/14) – 1/4
= (-1 )/7 – 1/4
= (-4-7 )/28
= (-11 )/28 (Answer)
Summary: By using the properties of commutativity for addition, commutativity for multiplication and distributivity of multiplication over subtraction, the answers for the expressions (i) – 2/3 × 3/5 + 5/2 – 3/5 × 1/6 and (ii) 2/5 × (– 3/7 ) – 1/6 × 3/2 + 1/14 × 2/5 are 2 and (-11 )/28 respectively.
2. Write the additive inverse of each of the following:
(i) 2/8
(ii) (-5)/9
(iii)(-6)/(-5)
(iv) 2/(-9)
(v) 19/(-6)
Answers:
(i) Since 2/8 + ((-2)/8) = (2-2)/8 = 0/8 = 0, (-2)/8 is the additive inverse of 2/8 .
(ii) Since (-5)/9 + 5/9 = (-5 + 5)/9 = 0/9 = 0, 5/9 is the additive inverse of (-5)/9 .
(iii) Since (-6)/(-5) = 6/5 and 6/5 + ((-6)/5) = (6-6)/5 = 0/5 = 0, (-6)/5 is the additive inverse of (-6)/(-5) (or 6/5) .
(iv) Since 2/(-9) = (-2)/9 and (-2)/9 + 2/9 = (-2 + 2)/9 = 0/9 = 0, 2/9 is the additive inverse of 2/(-9) (or (-2)/9) .
(v) Since 19/(-6) = (-19)/6 and (-19)/6 + 19/6 = (-19 + 19)/6 = 0/6 = 0, 19/6 is the additive inverse of 19/(-6) (or (-19)/6) .
3. Verify that: – (–x) = x for:
(i) x = 11/15
(ii) x = – 13/17
Answers:
(i) We have, x = 11/15
The additive inverse of x = 11/15 is – x = (-11)/15 since 11/15 + ((-11)/15) = 0. The same equality 11/15 + ((-11)/15) = 0, shows that the additive inverse of (-11)/15 is 11/15 . Therefore, – ((-11)/15) = 11/15 i.e. – (– x) = x (Proved)
(ii) We have, x = (-13)/17
The additive inverse of x = (-13)/17 is – x = 13/17 since (-13)/17 + 13/17 = 0. The same equality(-13)/17 + 13/17 = 0, shows that the additive inverse of (-13)/17 is 13/17 . Therefore, – ((-13)/17) = 13/17 i.e. – (– x) = x (Proved).
4. Find the multiplicative inverse of the following:
(i) – 13
(ii) (-13)/19
(iii) 1/5
(iv) (-5)/8 × (-3)/7
(v) – 1 × (-2)/5
(vi) – 1
Answers:
(i) – 13
Since (– 13) × (1/(-13)) = 1, the multiplicative inverse of – 13 is 1/(-13) or (-1)/13 (rational number).
(ii) (-13)/19
Since ((-13)/19) × (19/(-13)) = 1, the multiplicative inverse of (-13)/19 is 19/(-13) or (-19)/13(rational number).
(iii) 1/5
Since 1/5 × 5/1 = 1, the multiplicative inverse of 1/5 is 5 or 5/1 (rational number).
(iv) (-5)/8 × (-3)/7
Since (-5)/8 × (-3)/7 = (-5 × (-3))/(8 × 7) = 15/56 and 15/56 × 56/15 = 1, the multiplicative inverse of ((-5)/8 × (-3)/7) is 56/15 .
(v) – 1 × (-2)/5
Since – 1 × (-2)/5 = ((-1) × (-2))/5 = 2/5 and 2/5 × 5/2 = 1, the multiplicative inverse of (– 1 × (-2)/5) is 5/2 .
(vi) – 1
Since – 1 × (–1) = 1, the multiplicative inverse of – 1 is – 1 or (-1)/1 (rational number).
Summary: The multiplicative inverses of: (i) – 13 is (-1)/13 , (ii) (-13)/19 is (-19)/13 , (iii) 1/5 is 5/1 , (iv) (-5)/8 × (-3)/7 is 56/15 , (v) – 1 × (-2)/5 is 5/2 , (vi) – 1 is – 1.
6. Multiply 6/13 by the reciprocal of (-7)/16 .
Answer:
The reciprocal of (-7)/16 is (-16)/7 .
Now, 6/13 × (-16)/7 = (6 × (-16))/(13 × 7) = (-96)/91 .
Summary: If we multiply 6/13 by the reciprocal of (-7)/16 we get the product = (-96)/91 .
7. Tell what property allows you to compute 1/3 × (6 × 4/3) as (1/3 × 6) × 4/3 .
Answer: The expression is of the form a × (b × c) = (a × b) × c, where a = 1/3 , b = 6 and c = 4/3 . Hence, the property used is associative property of multiplication.
8. Is 8/9 the multiplicative inverse of – 11/8 ? Why or why not?
Answer: We have, – 11/8 = (-9)/8 and (-9)/8 × 8/9 = – 1, Therefore, we conclude that 8/9 is not the multiplicative inverse of – 11/8 because their product is not equal to 1.
9. 0.3 the multiplicative inverse of 31/3 ? Why or why not?
Answer: We have 0.3 = 3/10 and 31/3 = 10/3. Now, 3/10 × 10/3 = 1 and hence we conclude that 0.3 is the multiplicative inverse of 31/3.
10. Write.
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Answers:
(i) The rational number that does not have a reciprocal.
0 can be written as the rational number 0/1 . The reciprocal of 0/1 = 1/0 which is undefined. Therefore, the required number that does not have a reciprocal is 0.
(ii) The rational numbers that are equal to their reciprocals.
1 can be written as the rational number 1/1 and the reciprocal of 1/1 is also 1/1.
Similarly, – 1 can be written as the rational number (-1)/1 and the reciprocal of (-1)/1 is 1/(-1) which is = (-1)/1.
Therefore, 1 and – 1 are rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
0 can be written as the rational number 0/1 . The negative of 0/1 is (-0)/1 which is also equal to 0.
Therefore, 0 is the rational number that is equal to its negative.
Summary: (i) 0 is the rational number that does not have a reciprocal. (ii) 1 and – 1 are rational numbers that are equal to their reciprocals. (iii) 0 is the rational number that is equal to its negative.
11. Fill in the blanks.
(i) Zero has _______ reciprocal.
(ii) The numbers ______and _______are their own reciprocals.
(iii) The reciprocal of – 5 is __.
(iv) Reciprocal of 1/x, where x ≠ 0 is _______.
(v) The product of two rational numbers is always a _______.
(vi) The reciprocal of a positive rational number is _______.
Answers:
(i) Zero has no reciprocal.
(ii) The numbers 1 and – 1 are their own reciprocals.
(iii) The reciprocal of – 5 is (-1)/5.
(iv) Reciprocal of 1/x, where x ≠ 0 is x.
(v) The product of two rational numbers is always a rational number.
(vi) The reciprocal of a positive rational number is positive.
Exercise 1.2 Page No: 20 (Old Textbook):
1. Represent these numbers on the number line.
(i) 7/4
(ii) (-5)/6
Answers:
(i) 7/4
Since the denominator of the fraction is 4, we divide the number line between the whole numbers into 4 equal parts. The length of the line between 0 and 1 is divided into 4 equal parts and the length of the line between 1 and 2 is divided into 4 equal parts. To get 7/4, we count 7 markings of length 1/4 each on the right of zero and starting from 0. The seventh marking is 7/4 as shown below:
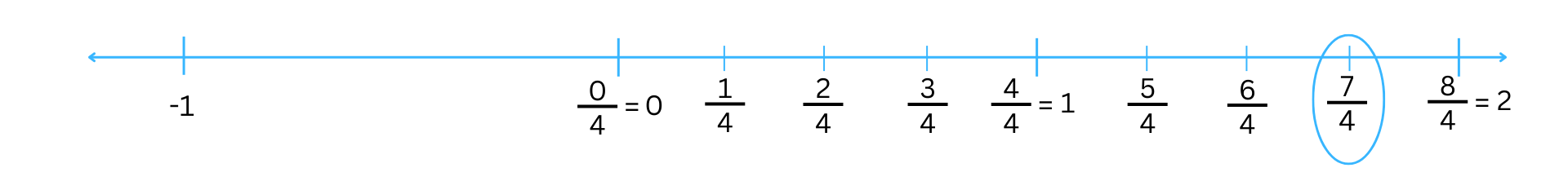
(ii) (-5)/6
Since the denominator of the fraction is 6, we divide the number line between the whole numbers 0 and – 1 into 6 equal parts. To get (-5)/6, we count 5 markings of length 1/6 each on the left of zero and starting from 0. The fifth marking is (-5)/6 as shown below:
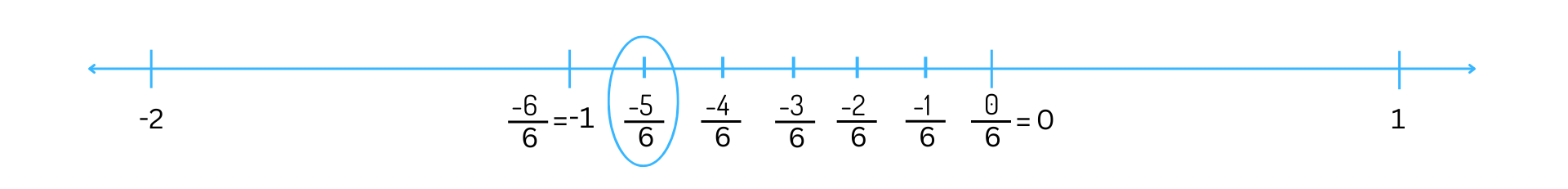
2. Represent (-2)/11, (-5)/11, (-9)/11 on a number line.
Answer:
Since the denominator of the fraction is 11, we divide the number line between the whole numbers 0 and – 1 into 11 equal parts. To get (-2)/11, we count 2 markings of length 1/11 each on the left of zero and starting from 0. The second marking is (-2)/11. To get (-5)/11, we count 5 markings of length 1/11 each on the left of zero and starting from 0. The fifth marking is (-5)/11. To get (-9)/11, we count 9 markings of length 1/11 each on the left of zero and starting from 0. The ninth marking is (-9)/11. The three numbers are marked on the number line below:

3. Write five rational numbers which are smaller than 2.
Answer:
We can write 2 as 20/10. Thus we can say that five rational numbers which are small than 2 are 19/10, 18/10, 10/10, 9/10, 1/10.
4. Find ten rational numbers between (-2)/5 and 1/2.
Answer:
We first convert (-2)/5 and 1/2 to rational numbers with the same denominator.
(-2)/5 = (-2 × 4)/(5 × 4) = (-8)/20 and 1/2 = (1 × 10)/(2 × 10) = 10/20
Thus ten rational numbers between (-2)/5 and 1/2 are (-7)/20, (-6)/20, (-5)/20, (-4)/20, (-3)/20, (-2)/20, (-1)/20, 0, 1/20, 2/20.
5. Find five rational numbers between.
(i) 2/3 and 4/5
(ii) (-3)/2 and 5/3
(iii) 1/4 and 1/2
Answers:
(i) 2/3 and 4/5
Let us make the denominators of both numbers = 60.
2/3 = (2 × 20)/(3 × 20) = 40/60 and 4/5 = (4 × 12)/(5 × 12) = 48/60
Five rational numbers between 40/60 and 48/60 are 41/60, 42/60, 43/60, 44/60, 47/60.
(ii) (-3)/2 and 5/3
Let us make the denominators of both numbers = 6.
(-3)/2 = (-3 × 3)/(2 × 3) = (-9)/6 and 5/3 = (5 × 2)/(3 × 2) = 10/6
Five rational numbers between (-9)/6 and 10/6 are (-8)/6, (-7)/6, 3/6, 5/6, 6/6.
(iii) 1/4 and 1/2
Let us make the denominators of both numbers = 24.
1/4 = (1 × 6)/(4 × 6) = 6/24 and 1/2 = (1 × 12)/(2 × 12) = 12/24
Five rational numbers between 6/24 and 12/24 are 7/24, 8/24, 9/24, 10/24, 11/24.
6. Write five rational numbers greater than -2.
Answer: We can write – 2 as (-20)/10. Thus we can say that five rational numbers which are greater than – 2 are (-19)/10, (-10)/10, (-1)/10, 5/10, 10/10.
7. Find ten rational numbers between 3/5 and 3/4.
Answer: Let us make the denominators of both numbers = 80.
3/5 = (3 × 16)/(5 × 16) = 48/80 and 3/4 = (3 × 20)/(4 × 20) = 60/80
Five rational numbers between 48/80 and 60/80 are 49/80, 50/80, 51/80, 52/80, 53/80, 54/80, 55/80, 56/80, 57/80, 58/80.
Extra Questions to Complement Solutions to NCERT Class 8 Mathematics Chapter 1 Rational Numbers:
(A) Very Short Answer Type Questions:
1. Find the reciprocal of 5/6 and then show how to get the number back.
Answer:
Reciprocal of 5/6 is 6/5 since 5/6 × 6/5 = 1.
We get the number back by dividing 1 by 6/5: 1 ÷ 6/5 = 5/6.
2. Which is greater: 1/10 or (-1)/10 ?
Answer:
1/10 lies to the right of 0 in the number line and (-1)/10 lies to the left of 0 on the number line. Therefore, 1/10 is greater than (-1)/10.
3. What happens when you divide a rational number by 0?
Answer:
Let us take a rational number 2/3.
We have 2/3 ÷ 0 = 2/3 ÷ 0/1 = 2/3 × 1/0 , which is undefined.
4. Show using 0 that the division of rational numbers is not commutative.
Answer:
Let us take the rational numbers 5/6 and 0.
0 can be written as 0/1.
We have 5/6 ÷ 0/1 = 0 = 5/6 × 1/0 which is undefined. Therefore, there is no need to evaluate the other division 0/1 ÷ 5/6 which is equal to 0.
Hence, it is proved that division of rational numbers is not commutative.
5. Which part of the number line is the negative part?
Answer:
The part of the number line to the left of 0 on the number line.
6. Is negative – 8 a rational number?
Answer:
– 8 can be written as (-8)/1, which is a negative rational number.
7. What is the largest rational number?
Answer:
There are countless rational numbers, so the largest number is undefined.
8. Give a rational number which is also an integer between – 1 and 1.
Answer:
0 is an integer between – 1 and 1. 0 can also be written in rational number form as 0/1.
9. What is the additive inverse and multiplicative inverse of a/b ?
Answer:
Since a/b + ((-a)/b) = 0, we can say that the additive inverse of a/b is (-a)/b.
Since a/b × b/a = 1, we can say that the multiplicative inverse of a/b is b/a.
10. Give a number which has the same additive inverse as itself.
Answer:
The number which as the same additive inverse as itself is 0.
(B) Multiple Choice Questions (MCQ):
1. Look at the following expression: 3/7 × 1/5 – 2/5 × 3/7. What properties can you use to easily simplify the expression?
(a) Commutativity
(b) Commutativity and associativity
(c) Associativity
(d) Commutativity and distributivity
Answer: Correct answer: (d) Commutativity and distributivity.
Solution:
3/7 × 1/5 – 2/5 × 3/7
= 3/7 × 1/5 – 3/7 × 2/5 (Using commutativity of multiplication)
= 3/7 × (1/5 – 2/5) (Using distributivity of multiplication over subtraction)
= 3/7 × ((1 – 2)/5)
= 3/7 × ((- 1)/5)
= (3 × (-1))/(7 × 5)
= (-3)/35
2. Which is the largest rational number among the following: 5/2, 6/5, 13/10, 3/10
(a) 5/2
(b) 6/5
(c) 13/10
(d) 3/10
Answer: Correct answer: (a) 5/2.
Solution:
Let us make the denominators of all the fractions = 10.
5/2 = (5 × 5)/(2 × 5) = 25/10
6/5 = (6 × 2)/(5 × 2) = 12/10
The denominators of the fractions 13/10 and 3/10 are both already = 10.
By comparing we get,
25/10 > 13/10 > 12/10 > 3/10
Hence, the largest rational number = 25/10 or 5/2.
3. Which of the following rational numbers is the equivalent of 6/5 ?
(a) 36/31
(b) 90/75
(c) 12/11
(d) 24/21
Answer: Correct answer: (b) 90/75.
We can see that 90/75 = (90 ÷ 15)/(75 ÷ 15) = 6/5 .
4. If 7/8 × x = 1/56 , the value of x is:
(a) 1/42
(b) 1/49
(c) 1/8
(d) 1/64
Answer: Correct answer: (b) 1/49.
We have 7/8 × x = 1/56
or, x = 1/56 × 8/7
or, x = 1/49
5. 1 can be written as the rational number(s):
(a) 7/7
(b) (-7)/(-7)
(c) Both (a) and (b)
(d) None
Answer: Correct answer: (c) Both (a) and (b).
We note:
7/7 = (7 ÷ 7)/(7 ÷ 7) = 1/1 = 1
(-7)/(-7) = (-7 ÷ (-7))/(-7 ÷ (-7)) = 1/1 = 1
(C) Short and Long Answer Type Questions:
1. Evaluate the following:
(i) 25/36 × 7/6 × 6/5
(ii) 1/3 × 25 × 9 × 1/5
Answers:
(i) 25/36 × 7/6 × 6/5
We have 25/36 × 7/6 × 6/5
= (5 × 5)/(6 × 6) × 7/6 × 6/5
= 5/6 × 5/6 × 7/6 × 6/5
= 5/6 × 5/6 × 6/5 × 7/6
= (5/6 × 6/5) × (5/6 × 7/6) (Using commutativity and associativity of multiplication of rational numbers)
= 1 × 35/36 (5/6 and 6/5 are reciprocals)
= 35/36
(ii) 1/3 × 25 × 9 × 1/5
= 1/3 × 9 × 25 × 1/5 (Using commutativity of multiplication)
= (1/3 × 9) × (25 × 1/5) (Using associativity of multiplication)
= 3 × 5
= 15
2. Evaluate the following:
(i) 7/5 × ((-3)/12) + 7/5 × 5/12
(ii) 9/16 × 4/12 + 9/16 × ((-3)/9)
Answers:
(i) 7/5 × ((-3)/12) + 7/5 × 5/12
= 7/5 × ((-3)/12 + 5/12) (Using distributivity of multiplication over addition)
= 7/5 × 2/12
= 7/30
(ii) 9/16 × 4/12 + 9/16 × ((-3)/9)
= 9/16 × [4/12 + ((-3)/9)] (Using distributivity of multiplication over addition)
= 9/16 × [4/(3 × 4) + ((-3)/(3 × 3))]
= 9/16 × [1/3 + ((-1)/3)]
= 9/16 × [(1 – 1)/3]
= 9/16 × 0
= 0
3. Show how the mean of the rational numbers 1/6 and 1/5 compares to the two numbers.
Answer:
The mean of the given rational numbers 1/6 and 1/5 is:
(1/6 + 1/5) ÷ 2 = ((5 + 6)/30) ÷ 2 = 11/30 ÷ 2 = 11/60
The numbers can be written as 1/6 = (1 × 10)/(6 × 10) = 10/60 and 1/5 = (1 × 12)/(5 × 12) = 12/60.
As you can see the mean 10/60 < 11/60 < 12/60 and lies in the middle between 10/60 and 12/60.
Therefore, 1/6 < 11/60 < 1/5 and the mean 11/60 lies right in the middle between 1/6 and 1/5.
4. Find three negative rational numbers and three positive rational numbers between (-1)/2 and 1/3.
Answer:
Let us make the denominators of both rational numbers = 12.
(-1)/2 = (-1 × 6)/(2 × 6) = (-6)/12 and 1/3 = (1 × 4)/(3 × 4) = 4/12
Therefore, three negative rational numbers are (-5)/12 , (-3)/12 , (-1)/12 and three positive rational numbers are 1/12 , 2/12 and 3/12.
5. Represent 11/4 and 11/2 on the number line.
Answer:
11/4 = 5/4 and 11/2 = 3/2 = (3 × 2)/(2 × 2) = 6/4
Since we have converted the denominators of both fractions to 4, we divide the number line between the whole numbers into 4 equal parts. The length of the line between 0 and 1 is divided into 4 equal parts and the length of the line between 1 and 2 is divided into 4 equal parts. To get 5/4, we count 5 markings of length 1/4 each on the right of zero and starting from 0. The fifth marking is 5/4. To get 6/4, we count 6 markings of length 1/4 each on the right of zero and starting from 0. The sixth marking is 6/4. The rational numbers 5/4 and 6/4 marked on the number line is shown below:

6. Rational numbers are closed under division. True/False?
Answer:
We note that 5/4 ÷ 3/4 = 5/3 and 8/7 ÷ 5/6 = 48/35 .
Hence, it may seem that the division of any two rational numbers yields another rational number.
However, if you divide any rational number a by 0, a ÷ 0 is not defined.
Hence, we conclude that rational numbers are not closed under division. And the given statement is False.
7. Division is associative for rational numbers. True/False?
Answer:
We note that 5/4 ÷ (3/4 ÷ 1/2)
= 5/4 ÷ (3/4 × 2/1)
= 5/4 ÷ 3/2
= 5/4 × 2/3
= 5/6
Also we note that (5/4 ÷ 3/4) ÷ 1/2
= (5/4 × 4/3) ÷ 1/2
= 5/3 ÷ 1/2
= 5/3 × 2/1
= 10/3
Therefore, 5/4 ÷ (3/4 ÷ 1/2) is not equal to ( 5/4 ÷ 3/4) ÷ 1/2 and so division is not associative for rational numbers. Hence, the above statement is False.
8. A father takes 1/2 out of an entire cake and divides the remaining equally among his three daughters. What is the share of each daughter?
Answer:
The father takes 1/2 out of an entire cake.
The part of the cake that remains = (1 – 1/2) = 1/2 part.
The father divides the remaining equally among his three daughters.
Therefore, the part of the cake that each daughter gets (1/2 ÷ 3) = (1/2 × 1/3) = 1/6 part.
9. Show using the number line which one of 3/4 and 7/8 is greater.
Answer:
We make the denominators of both fractions = 8.
3/4 = (3 × 2)/(4 × 2) = 6/8
Since we have converted the denominators of both fractions to 8, we divide the length of the number line between 0 and 1 is divided into 8 equal parts. To get 6/8, we count 6 markings of length 1/8 each on the right of zero and starting from 0. The sixth marking is 6/8. To get 7/8, we count 7 markings of length 1/8 each on the right of zero and starting from 0. The seventh marking is 7/8. The required number line is shown below:

Since 7/8 lies to the right of 6/8 , we conclude that 7/8 is greater than 6/8 or 7/8 is greater than 3/4.
10. The sum of Ram, Shyam and Sachin’s marks in an exam is 300. Ram and Shyam’s marks are equal and Sachin’s marks is 1/2 of that. What is Ram, Shyam and Sachin’s marks individually?
Answer:
Let marks obtained by Ram = marks obtained by Shyam = x.
Therefore, Sachin’s marks = x/2.
The sum of Ram, Shyam and Sachin’s marks in the exam = 300.
Therefore, x + x + x/2 = 300
or, 5x/2 = 300
or, x = 120
Therefore, x/2 = 60
Marks obtained by Ram = 120 marks.
Marks obtained by Shyam = 120 marks.
Marks obtained by Sachin = 60 marks.
Fill in the Blanks:
(a) Multiplicative inverse of a negative rational number is a _______ rational number.
(b) A rational number immediately to the left of 0 on the number line is _______.
(c) Between the rational numbers 9/32 and 5/16 the greater number is _______.
(d) There are______ negative rational numbers.
(e) There are ______ positive rational numbers to the right of 3009/16.
Answers:
(a) Multiplicative inverse of a negative rational number is a negative rational number.
(b) A rational number immediately to the left of 0 on the number line is negative.
(c) Between the rational numbers 9/32 and 5/16 the greater number is 5/16.
(d) There are infinite negative rational numbers.
(e) There are infinite positive rational numbers to the right of 3009/16.
++++++++++++++
Frequently Asked Questions (FAQs) on NCERT Solutions to Class 8 Mathematics Chapter 1 Rational Numbers:
Our team of Indian and foreign-educated scientists and engineers have shown all the major problems solving techniques you need to know for this chapter. You will have a good idea about how to solve typical problems after studying the solutions and extra material. The problem-solving methods are clear and logical and you will understand them easily.
The free PDF version of the solutions is also available for download anytime! We are preparing lots more study material and resources for you, so subscribe to our email list to be among the first to access them.
The following topics are covered:
1.1 – Introduction
1.2 – Properties of Rational Numbers
Here are the number of problems for the chapter:
Exercise 1.1 – 3 Problems
Of course! You can download PDF version of educationroundtheworld.com’s NCERT Solutions for Class 8 Mathematics Chapter 1 Rational Numbers anytime! We have also included the self-designed extra problems in the PDF version! Please look towards the top of the page to find the button to download the document!
The most important part of the chapter is the properties of rational numbers. Understand how the properties are derived and how to use to solve problems. Practice is essential for understanding how to use these properties. Our exercise solutions and set of extra problems are an excellent place to begin.
If you need additional coaching, feel free to contact us anytime. We will assign you a dedicated teacher-mentor who will take care of all your requirements. Feel free to reach out to us anytime.
In addition to coaching and exam preparation we believe in counselling young students regarding their future careers. We have found this approach to be very beneficial for young minds to flower. If that sounds good to you, then reach out us! We will assign you a friendly teacher-mentor who will take care of all your needs.
We provide expert one-on-one coaching and mentoring to you depending on your convenience and needs – have it completely your way! Book an appointment now!


