Solutions to NCERT Class 9 Mathematics Chapter 1 Number Systems:

Hello students and welcome to Class 9! We have included excellent solutions to all Chapter 1 textbook exercises and a plethora of carefully designed extra questions right here to help you learn the topic fast. If you understand the problems in this material and practise them on your own, you will be confident as far as this chapter is concerned. We only suggest that you practise the problems on your own while looking at the solutions, for maximum benefit.

Solutions to Exercise 1.1 (Page 5) of NCERT Class 9 Mathematics Chapter 1 Number Systems:

1. Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q ≠ 0?
Answer:
Yes, zero is a rational number. This is because zero can be written in the form of 0 ÷ any non-zero integer. 0 can be written in the form p/q, where p and q are integers and q ≠ 0 as follows: 0/2 = 0 and 0/5 = 0.

2. Find six rational numbers between 3 and 4.
Answer:
Since we want six numbers, we write 3 and 4 as rational numbers with denominator 6 + 1, i.e. 3 = 21/7 and 4 = 28/7.
Therefore, six rational numbers between 3 and 4 are 22/7, 23/7, 24/7, 25/7, 26/7, 27/7.

3. Find five rational numbers between 3/5 and 4/5.
Answer:
Since we want 5 numbers, we multiply numerator and denominator of both fractions with 5 + 1 = 6.
3/5 = (3 × 6)/(5 × 6) = 18/30 and 4/5 = (4 × 6)/(5 × 6) = 24/30
Therefore, five rational numbers between 3/5 and 4/5 are 19/30, 20/30, 21/30, 22/30, 23/30.

4. State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
Answer:
The statement is True.
Natural numbers represent all integers starting from 1 to infinity. Whole numbers represent all integers starting from 0 to infinity. The set of whole numbers = set of natural numbers + 0. Therefore, every natural number is a whole number.

(ii) Every integer is a whole number.
Answer:
The statement is False. Integers can be both positive and negative, whereas whole numbers only include 0 and positive integers. Negative integers are not whole numbers.

(iii) Every rational number is a whole number.
Answer:
The statement is False. Rational numbers can be written in the form p/q, where p and q are integers and q ≠ 0. Whole numbers represent all integers starting from 0 to infinity. Examples of rational numbers are 7/8, (-11)/4, 2/3, 6/7 , which are not whole numbers.

Solutions to Exercise 1.2 (Page 9) of NCERT Class 9 Mathematics Chapter 1 Number Systems:

1. State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number.
Answer:
The statement is True. Real numbers comprise all rational numbers + all irrational numbers. Therefore, every irrational number is a real number. For example, √5 is an irrational number which is also a real number.

(ii) Every point on the number line is of the form √m, where m is a natural number.
Answer:
The statement is False. For example, the number √(1/2) lies on the number line, but m = 1/2 which is not a natural number.

(iii) Every real number is an irrational number.
Answer:
The statement is False. Real numbers include all rational numbers and all irrational numbers.

2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Answer:
No, square roots of all positive integers are not irrational, they can be rational as well. An example of the square root of a number that is a rational number is √4 = 2. Here 2 is a rational number because it can be written as 2 = 2/1.

3. Show how √5 can be represented on the number line.
Answer:
√5 can be represented on the number line by following the given procedure:
Step 1: Take AB of length 2 units on the number line.
Step 2: At B construct a perpendicular BC of length 1 unit.
Step 3: Join AC to form right-angled triangle ABC.
Step 4: Using Pythagoras theorem we get, AB² + BC² = AC² or 2² + 1² = AC² or AC² = 5 or AC = √5.
Step 5: Using a compass with centre A and radius AC, draw an arc which intersects the number line. This point of intersection is at a distance √5 from O.

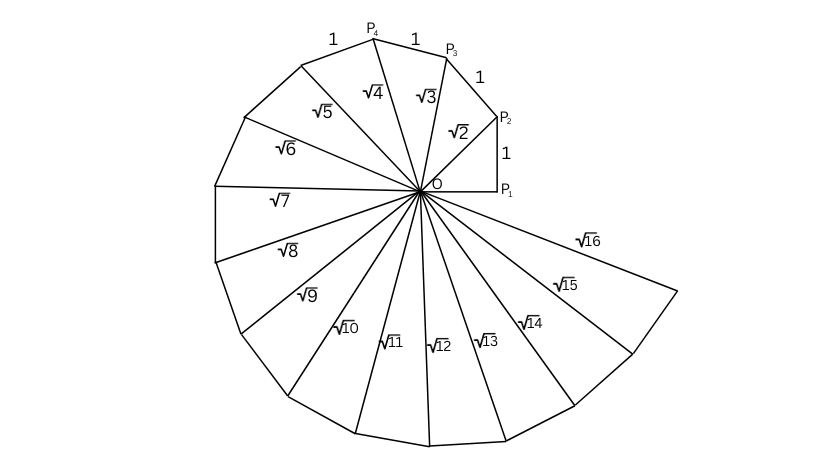
4. Classroom activity (Constructing the ‘square root spiral’) : Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁ P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂ P₃ perpendicular to OP₂ . Then draw a line segment P₃ P₄ perpendicular to OP₃ . Continuing in this manner, you can get the line segment P_n–1P_n by drawing a line segment of unit length perpendicular to OP_n–1. In this manner, you will have created the points P₂ , P₃ ,…., P_n ,… ., and joined them to create a beautiful spiral depicting 2, 3, 4, …

Answer:

Step 1: Take a point O and draw a horizontal line segment OP₁ of unit length.

Step 2: Now draw a line segment P₁P₂ perpendicular to OP₁ of unit length.

Step 3: Join OP₂. OP₂ = √(1²+ 1² ) = √2.

Step 4: Now draw a line segment P₂ P₃ perpendicular to OP₂ of unit length.

Step 5: Join OP₃. OP₃ = √((√2)²+ 1² ) = √3.

Similarly, continue the process until you get the beautiful spiral shown below:

Solutions to Exercise 1.3 (Page 14) of NCERT Class 9 Mathematics Chapter 1 Number Systems:

1. Write the following in decimal form and say what kind of decimal expansion each has:
(i) 36/100
(ii) 1/11
(iii) 4 1/8
(iv) 3/13
(v) 2/11
(vi) 329/400

Answers:

(i) 36/100

36/100 = 0.36
The decimal expansion is terminating.

(ii) 1/11

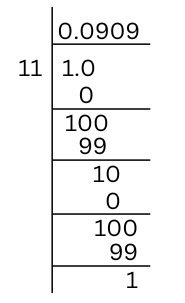
1/11 =
So, the decimal expansion is non-terminating and recurring.

(iii) 4 1/8

4 1/8 = 33/8

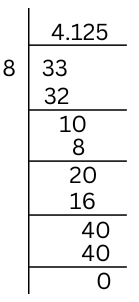
33/8 = 4.125
The decimal expansion is terminating.

(iv) 3/13

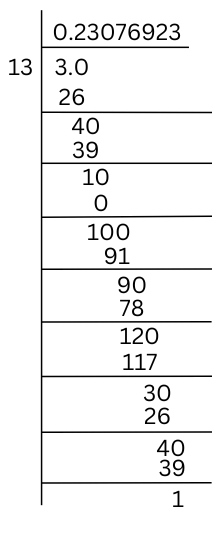
$latex \frac{3}{13}=0.\overline{230769}$

(v) 2/11

2/11 =

(vi) 329/400

329/400 = 0.8225
The decimal is terminating.

Summary:
The decimal expansions of (i) 36/100 , (iii) 41/8 and (vi) 329/400 are terminating and the decimal expansions of (ii) 1/11 , (iv) 3/13 and (v) 2/11 are non-terminating recurring.

2. You know that 1/7 = . Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of 1/7 carefully.]

Answer:

(i) 2/7
We get 2 as the remainder after the second step in the long division.
Hence, the quotient will start from after the second decimal place = 0.285714.
Therefore,

$latex \frac{2}{7}=0.\overline{285714}$

(ii) 3/7
We get 3 as the remainder after the first step in the long division.
Hence, the quotient will start from after the first decimal place = 0.428571.
Therefore,

$latex \frac{3}{7}=0.\overline{428571}$

(iii) 4/7
We get 4 as the remainder after the fourth step in the long division.
Hence, the quotient will start from after the fourth decimal place = 0.571428.
Therefore,

$latex \frac{4}{7}=0.\overline{571428}$

(iv) 5/7
We get 5 as the remainder after the fifth step in the long division.
Hence, the quotient will start from after the fifth decimal place = 0.714285.
Therefore,

$latex \frac{5}{7}=0.\overline{714285}$

(v) 6/7
We get 6 as the remainder after the third step in the long division.
Hence, the quotient will start from after the third decimal place = 0.857142.
Therefore,

$latex \frac{6}{7}=0.\overline{857142}$

3. Express the following in the form p/q , where p and q are integers and q ≠ 0.

(i) $latex 0.\overline{6}$

(ii) $latex 0.4\overline{7}$

(iii) $latex 0.\overline{001}$

Answers:

Let x = 0.6666…
10x = 10 × 0.6666…
or 10x = 6.666…
We observe,
10x = 6 + x
or, 10x – x = 6
or, 9x = 6
or, x = 6/9
or, x = 2/3
Therefore,

$latex 0.\overline{6}$ = 2/3 (Answer)

= 4/10 + 0.777/10
Let x = 0.777…
10x = 10 × 0.777… = 7.77…
We observe,
10x = x + 7
or, 9x = 7
or, x = 7/9
Therefore, 0.777… = 7/9.

$latex 0.4\overline{7}$ = 0.4777… = 4/10 + 1/10 × 7/9 = 4/10 + 7/90 = 36/90 + 7/90 = 43/90

$latex 0.4\overline{7}$ = 43/90 (Answer)

Let x = 0.001001…
1000x = 1000 × 0.001001… = 1.001…
We observe,
1000x = 1 + x
or, 999x = 1
or, x = 1/999
Therefore,

$latex 0.\overline{001}$ = 1/999 (Answer)

4. Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Answer:
Let x = 0.9999…
10x = 10 × 0.9999… = 9.999…
10x = 9 + x
or, 9x = 9
or, x = 1
0.99999…. is almost equal to 1. Hence, the answer makes sense.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer.
Answer:
The division is shown below:

We stop the division when the remainder is 1.

Therefore,

$latex \frac{1}{17}=0.\overline{0588235294117647}$

6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
Let us look at examples of rational numbers whose decimal expansions are terminating.
3/16 = 0.1875
7/10 = 0.7
8/25 = 0.32
33/100 = 0.33
Let us examine the denominators of the above numbers.
16 = 2 × 2 × 2 × 2
10 = 2 × 5
25 = 5 × 5
100 = 2 × 2 × 5 × 5
As you can see, the denominators are multiples of 2 or multiples of 5 or both, for the decimal representation to be terminating.
Summary: The property q must satisfy for the rational number to have terminating decimal representations (expansions) is that it must be a multiple of 2 or multiple of 5 or both.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
√2 = 1.4142135
√17 = 4.1231056
√29 = 5.3851648

8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.
Answer:

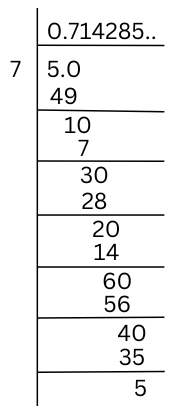
$latex \frac{5}{7}=0.\overline{714285}$

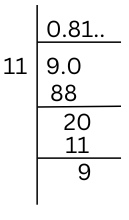
$latex \frac{9}{11}=0.\overline{81}$

three different irrational numbers between the rational numbers 5/7 and 9/11 are:

(i) 0.722627362783
(ii) 0.75839037847
(iii) 0.80103029403

Summary: Three different irrational numbers between the rational numbers 5/7 and 9/11 are (i) 0.722627362783, (ii) 0.75839037847, (iii) 0.80103029403.

9. Classify the following numbers as rational or irrational:

(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478
(v) 1.101001000100001…

Answers:

(i) √23

√23 = √23/1
Since √23 is not an integer, the number cannot be expressed in the form p/q (q ≠ 0), where p and q are integers. Hence, √23 is an irrational number.

(ii) √225

√225 = 15 = 15/1 = p/q where p and q are both integers and q ≠ 0. Therefore, √225 is a rational number.

(iii) 0.3796

0.3796 is a terminating decimal number therefore can be expressed as a rational number.

(iv) 7.478478

7.478478 is a terminating decimal number therefore can be expressed as a rational number.

(v) 1.101001000100001…

1.101001000100001… is a non-terminating non-recurring number and is therefore, an irrational number.

Summary: (ii) √225, (iii) 0.3796, (iv) 7.478478 are rational numbers and (i) √23 and (v) 1.101001000100001… are irrational numbers.

Solutions to Exercise 1.4 (Page 20) of NCERT Class 9 Mathematics Chapter 1 Number Systems:

1. Classify the following numbers as rational or irrational:

(i) 2 – √5
(ii) (3 + √23) – √23
(iii) (2√7)/(7√7)
(iv) 1/√2
(v) 2π

Answers:

(i) 2 – √5

2 is a rational number and √5 is irrational.
The difference of a rational number and an irrational number is always irrational.
Therefore, 2 – √5 is irrational.

(ii) (3 + √23) – √23

3 + √23) – √23
= 3 = 3/1 which is in the form p/q where p and q are both integers and q ≠ 0. Hence, (3 + √23) – √23 is a rational number.

(iii) (2√7)/(7√7)

(2√7)/(7√7)
= 2/7 ÷ √7/√7
= 2/7 ÷ 1
= 2/7 which is in the form p/q where p and q are both integers and q ≠ 0. Hence, (2√7)/(7√7) is a rational number.

(iv) 1/√2

1/√2 = (1√2)/(√2 √2) = √2/2
Here √2 is an irrational number and 2 is a rational number. Hence, the quotient will be an irrational number.

(v) 2π

2π = 2 × 3.14….

Here 2 is a rational number and 3.14…. is an irrational number. Therefore, the product of the two is an irrational number.
Summary: (ii) (3 + √23) – √23, (iii) (2√7)/(7√7) are rational numbers and (i) 2 – √5 , (iv) 1/√2 and (v) 2π are irrational numbers.

2. Simplify each of the following expressions:

(i) (3 + √3)(2 + √2)
(ii) (3 + √3)(3 – √3)
(iii) (√5 + √2)2
(iv) (√5 – √2) (√5 + √2)

Answers:

(i) (3 + √3)(2 + √2)

= 3 × 2 + 3 × √2 + √3 × 2 + √3 × √2
= 6 + 3√2 + 2√3 + √6 (Answer)

(ii) (3 + √3)(3 – √3)
= (3)² – (√3)²
= 9 – 3
= 6 (Answer)

(iii) (√5 + √2)²
= (√5)² + 2 × √5 × √2 + (√2)²
= 5 + 2√10 + 2
= 7 + 2√10 (Answer)

(iv) (√5 – √2) (√5 + √2)
= (√5)² – (√2)²
= 5 – 2
= 3 (Answer)

Summary: The simplified value of (i) (3 + √3)(2 + √2) is 6 + 3√2 + 2√3 + √6, that of (ii) (3 + √3)(3 – √3) is 6, that of (iii) (√5 + √2)2 is 7 + 2√10 and that of (iv) (√5 – √2) (√5 + √2) is 3.

3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer:
There is no contradiction. When a length is measured with a scale or any other device, an approximate rational value is obtained. So, we may not realise that c or d is irrational.

4. Represent (√(9.3)) on the number line.
Answer:
To represent (√9.3) on the number line we follow the below steps:
Step 1: Mark AB = 9.3 units on a horizontal line.
Step 2: From B mark a distance of 1 unit and mark the new point as C. Mark the mid-point of AC as O.
Step 3: Draw a semicircle with centre O and radius OC.
Step 4: At B draw a perpendicular cutting the semicircle at D. BD = √9.3.

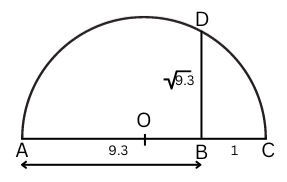
Step 5: Draw an arc with centre B and radius BD which cuts the number line at E. E represents √9.3.

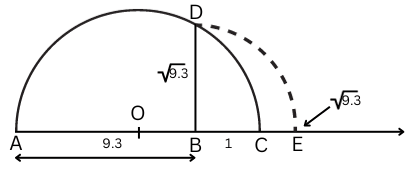
5. Rationalize the denominators of the following:

(i) 1/√7 (ii) 1/(√7-√6 )

(iii) 1/(√5 + √2 ) (iv) 1/(√7-2 )

Answers:

(i) 1/√7

1/√7
= 1/√7 × √7/√7 (Multiplying and dividing 1/√7 by √7)
= √7/7

(ii) 1/(√7-√6 )

Multiply and divide 1/(√7-√6 ) by √7 + √6 we get:
1/(√7-√6 )
= 1/(√7-√6 ) × (√7 + √6)/(√7 + √6)
= (√7 + √6)/((√7-√6)(√7 + √6))
= (√7 + √6)/((√7)^2- (√6)^2 ) [Since (a + b)(a – b) = a2 – b2]
= (√7 + √6)/(7-6)
= √7 + √6

(iii) 1/(√5 + √2 )

Multiply and divide 1/(√5 + √2 ) by √5 – √2 we get:
1/(√5 + √2 )
= 1/(√5 + √2 ) × (√5 – √2)/(√5 – √2)
= (√5- √2)/((√5)^2- (√2)^2 ) [Since (a + b)(a – b) = a2 – b2]
= (√5- √2)/(5 – 2)
= (√5- √2)/3

(iv) 1/(√7-2 )

Multiply and divide 1/(√7- 2 ) by √7 + 2 we get:
1/(√7-2 )
= 1/(√7-2 ) × (√7 + 2)/(√7 + 2)
= (√7 + 2)/((√7)^2- (2)^2 ) [Since (a + b)(a – b) = a2 – b2]
= (√7 + 2)/(7 – 4)
= (√7 + 2)/( 3)
Summary: The rationalized expression of (i) 1/√7 is √7/7 , that of (ii) 1/(√7-√6 ) is √7 + √6, that of (iii) 1/(√5 + √2 ) is (√5- √2)/3 and that of (iv) 1/(√7-2 ) is (√7 + 2)/( 3) .

Solutions to Exercise 1.5 (Page 23) of NCERT Class 9 Mathematics Chapter 1 Number Systems:

1. Find:
(i) 64^1/2
(ii) 32^1/5
(iii) 125^1/3

Answers:

(i) 64^1/2

64^1/2
= (8²)^1/2
= 8^{2 × 1/2}[Using (a^p )^q = a^pq]
= 8¹
= 8 (Answer)

(ii) 32^1/5

32^1/5
= (2⁵)^1/5
= 2^{5 × 1/5} [Using (a^p )^q = a^pq]
= 2¹
= 2(Answer)

(iii) 125^1/3

125^1/3
= (5³)^1/3
= 5^{3 × 1/3} [Using (a^p )^q = a^pq]
= 5¹
= 5 (Answer)

Summary: The value of (i) 64^1/2 = 8, the value of (ii) 32^1/5 = 2 and the value of (iii) 125^1/3 = 5.

2. Find:

(i) 9^3/2
(ii) 32^2/5
(iii) 16^3/4
(iv) 125^-1/3

Answer:

(i) 9^3/2

9^3/2
=(3²)^3/2
= 3^{2 × 3/2} [Using (a^p )^q = a^pq]
= 3³
= 27 (Answer)

(ii) 32^2/5

32^2/5
= (2⁵)^2/5
= 2^{5 × 2/5}[Using (a^p )^q = a^pq]
= 2²
= 4 (Answer)

(iii) 16^3/4

16^3/4
=(2⁴)^3/4
= 2^{4 × 3/4}[Using (a^p )^q = a^pq]
= 2³
= 8 (Answer)

(iv) 125^-1/3

125^-1/3
= (5³)^-1/3
= 5^{3 × -1/3}[Using (a^p )^q = a^pq]
= 5^-1
= 1/5 (Answer)

Summary: The value of (i) 9^3/2 = 27, the value of (ii) 32^2/5 = 4, the value of (iii) 16^3/4 = 8 and the value of (iv) 125^-1/3 = 1/5.

3. Simplify:

(i) 2^2/3 × 2^1/5
(ii) (1/3³)⁷
(iii) (11)^1/2/(11)^1/4
(iv) 7^1/2 . 8^1/2

Answers:

(i) 2^2/3 × 2^1/5

2^2/3 × 2^1/5
= 2^{2/3 + 1/5} (Since a^p.a^q = a^{p + q})
= 2^13/15

(ii) (1/3³)⁷

(1/3³)⁷
= (3^-3)⁷ [1/aⁿ = a^-n]
= 3^{-3 × 7} [Using (a^p )^q = a^pq]
= 3^-21

(iii) (11)^1/2/(11)^1/4

(11)^1/2/(11)^1/4
= (11)^{1/2 – 1/4} [Since a^p/a^q = a^{p – q} ]
= (11)^1/4

(iv) 7^1/2 . 8^1/2

7^1/2 . 8^1/2
= (7 × 8)^1/2 [Since a^pb^p = (ab)^p]
= 56^1/2

Extra Questions to Complement Solutions to NCERT Class 9 Mathematics Chapter 1 Number Systems:

(A) Multiple Choice Questions (MCQ):

1. A real number is:

(A) The set of all rational numbers
(B) The set of all irrational numbers
(C) The set of all rational and irrational numbers
(D) Either rational or irrational

Answer: (c) The set of all rational and irrational numbers

2. How many irrational numbers between 5 and 6?

(A) None
(B) One
(C) Many but finite
(D) Infinite

Answer: (d) Infinite

3. If r is rational and s is irrational then:

(A) r + s is irrational and r/s is rational
(B) r + s is rational and r/s is irrational
(C) r + s and r/s are both rational
(D) r + s and r/s are both irrational

Answer: (D) r + s and r/s are both irrational

4. The decimal expansion of 1/3 is:

(A) Terminating
(B) Non-terminating
(C) Non-terminating recurring
(D) Non-terminating non-recurring

Answer: (C) Non-terminating recurring

1/3 = 0.3333… = 0.3 ̅ , which is non-terminating recurring.

5. The value of 6.999…in the form p/q , where p and q are integers and q ≠ 0, is:

(A) (6.9)/10
(B) (6.999)/1000
(C) 7
(D) 1/6

Answer: (C) 7

x = 6.999…
10x = 10 × 6.999…
or, 10x = 69.99…
We observe,
10x = 63 + x
or, 9x = 63
or, x = 63/9 = 7

6. 5√3 – √3 + 6√3
(A) 10√3
(B) 6√3
(C) -√3
(D) 3√3

Answer: (A) 10√3

5√3 – √3 + 6√3
= √3(5 – 1 + 6)
= √3(10)
= 10√3

7. √3 × √9 is equal to:

(A) 3√3
(B) 3
(C) √3
(D) √21

Answer: (A) 3√3

√3 × √9
= √3 × 3
= 3√3

8. Value of 729^-1/4:

(A) 1/(3√3)
(B) 1/27
(C) 1/√3
(D) 3^-2

Answer: (A) 1/(3√3)

729^-1/4
= (27²)^-1/4
= (27)^{2 × -1/4} [Using (a^p )^q = a^pq]
= (27)^-1/2
= (3 × 3²)^-1/2
= (3)^-1/2 × (3²)^-1/2 [Since (ab)^p = a^pb^p]
= (3)^-1/2 × (3)^{2 ×-1/2} [Using (a^p )^q = a^pq]
= (3)^-1/2 × (3)^-1
= 1/(3)^1/2 × 1/3
= 1/√3 × 1/3
= 1/(3√3)

9. Which of the following is equal to 1:

(A) (√9 + √8)( √9 – √8)
(B) √2
(C) √2 – 1
(D) 1/√2

Answer: (A) (√9 + √8)( √9 – √8)

(√9 + √8)( √9 – √8)
= (√9)² – (√8)²
= 9 – 8
= 1

10. Find the value of: (√2 + √3)²(√2 – √3)²

(A) √2 + √3
(B) 1
(C) √2 – √3
(D) – 1

Answer: (B) 1

(√2 + √3)²(√2 – √3)²
= (√2 + √3) (√2 – √3)(√2 + √3) (√2 – √3)
= [(√2)² – (√3)²] [(√2)² – (√3)²]
= (2 – 3)(2 – 3)
= (-1) × (-1)
= 1

(B) Short Answer Type Questions:

1. Square root of a prime number is always irrational. True/False? Explain with examples.
Answer:
Let us take the prime numbers 2, 3, 11, 17.
√2 = 1.414…
√3 = 1.732…
√11 = 3.3166…
√17 = 4.1231…
The decimal expansions of the square roots of these numbers are non-terminating non-recurring. Therefore, they are irrational.

2. Give a non-terminating repeating rational number between 1.5 and 1.7.
Answer:
is a non-terminating repeating rational number between 1.5 and 1.7.

3. Give an irrational number between 0 and 0.1.
Answer:
0.012328392… is an irrational number between 0 and 0.1.

4. Write 12 in the form of (√a + √b)².
Answer:
12 = 3 + 2.3 + 3
= (√3)² + 2. √3 √3 + (√3)²
= (√3 + √3)² [Since a + 2√ab + b = (√a + √b)²]

5. Simplify the following:

(i) √20 + 3√5 – √80

(ii) (3 + √5)(3 – √5)

Answer:

(i) √20 + 3√5 – √80

= √(2 ×2 ×5) + 3√5 – √(2 ×2 ×2 ×2×5)
= 2√5 + 3√5 – 2 × 2√5
= 2√5 + 3√5 – 4√5
= √5

(ii) (3 + √5)(3 – √5)

= (3)² – (√5)²
= 9 – 5
= 4

6. Rationalise the following:

(i) (10√2)/√5

(ii) (√2 + 1)/(√2 -1 )

Answer:

(i) (10√2)/√5

(10√2)/√5
= (10√2 × √5 )/(√5 × √5)
= (10√10 )/5
= 2√10

(ii) (√2 + 1)/(√2 -1 )

= ((√2 + 1) × (√2+1) )/((√2 -1) × (√2+1) )
= (√2 + 1)²/((√2)²– 1 ²)
= (2 + 2√2 + 1)/(2-1)
= 3 + 2√2

7. If (√2)³(√3)⁴ = 6a√2, find the value of a.
Answer:
(√2)³(√3)⁴ = 6a√2
or, √2 × √2 × √2 × √3 × √3 × √3 × √3 = 6a√2
or, 2√2 × 9 = 6a√2
or, 18√2 = 6a√2
or, a = (18√2 )/(6√2)
or, a = 3

8. Find the value of:

(i) √(√81-5)

(ii) √6/√2 – √12/2 + 4√3

Answer:

(i) √(√81-5)

= √(√(9²)-5)
= √((9²)^1/2-5)
= √(9^{2 × 1/2}-5)
= √(9-5)
= √4
= 2

(ii) √6/√2 – √12/2 + 4√3

= (√3×√2)/√2 – (√4×√3)/2 + 4√3
= √3 – (2×√3)/2 + 4√3
= √3 – √3 + 4√3
= 4√3

9. Find the value of: √(√(8+√64) )
Answer:
√(√(8+√64) )
= √(√(8+√(8² )) )
= √(√(8+8))
= √(√16)
= √4
= 2

10. Simplify: (2√12 + 4√8 + 3√12)/(2√(3 )+ 4√2 + 3√3)
Answer:
(2√12 + 4√8 + 3√12)/(2√(3 )+ 4√2 + 3√3)
= (2√4 × √3 + 4√4 × √2 + 3√4 × √3)/(2√(3 )+ 4√2 + 3√3)
= (2 × 2 × √3 + 4 × 2 × √2 + 3 × 2 × √3)/(2√(3 )+ 4√2 + 3√3)
= (4√3 + 8√2 + 6√3)/(2√(3 )+ 4√2 + 3√3)
= 2(2√3 + 4√2 + 3√(3))/(2√(3 )+ 4√2 + 3√3)
= 2

11. If (1/3^-7)^-7= (1/3)^a, find the value of a.
Answer:
(1/3^-7)^-7= (1/3)^a
or, (3⁷)^-7 = (1/3)^a(Since 1/aⁿ = a^-n)
or, 3^-49 = (1/3)^a [Using (a^p )^q = a^pq]
or, (1/3)⁴⁹ = (1/3)^a(Since a^-n = 1/aⁿ )
or, (1/3)⁴⁹= (1/3)^a[Since a^p/b^p = (a/b)^p]
or, a = 49

12. Which of the following numbers are rational and which are irrational:

(i) 0.121212…
(ii) 0.0112
(iii) 0.0123123123…
(iv) 0.12356284…

Answer:

(i) 0.121212…

This number is non-terminating repeating and hence is rational.

(ii) 0.0112

This number is terminating and hence is rational.

(iii) 0.0123123123…

This number is non-terminating repeating and hence is rational.

(iv) 0.12356284…

This number is non-terminating non-repeating and hence is irrational.

13. Find whether the following numbers are rational or irrational:

(i) √8 – 1

(ii) √9 – √4

Answer:

(i) √8 – 1

= 2√2 – 1
Here 2 is rational and √2 = 1.4142… is irrational.
When we multiply a rational number and an irrational number, the product is irrational.
Therefore,
2√2 is irrational.
When you subtract a rational number from an irrational number the result is irrational.
Therefore,
2√2 – 1 is an irrational number or √8 – 1 is irrational.

(ii) √9 – √4

= 3 – 2
= 1 which is a rational number because it can be expressed in the form p/q where q≠0.
Therefore, √9 – √4 is rational.

14. Give a rational number and an irrational number, with the irrational number being greater than the rational number between 1.5 and 1.6

Answer: The rational number can be 1.55 and the irrational number can be 1.5673892….

(C) Long Answer Type Questions:

1. x = (√2 – 1)/(√2 + 1) and y = (√2 + 1)/(√2 – 1), then find the value of x2 + y2.

Answer:

x – y = (√2 – 1)/(√2 + 1) – (√2 + 1)/(√2 – 1)
= ((√2 – 1)²– (√2 + 1)²)/((√2 + 1)(√2 – 1))
= (2 – 2√2 + 1 – 2 – 2√(2 )- 1)/((√2)²– 1)
= (- 4√2)/(2-1)
= – 4√2
xy = (√2 – 1)/(√2 + 1) × (√2 + 1)/(√2 – 1) = 1
Therefore, x² + y² = (x – y)² + 2xy = (-4√2)² + 2.1 = 32 + 2 = 34.

2. Express in the form p/q where q≠0.

Answer:

$latex x=0.\overline{7}$=0.7777…

10x = 7.777
Now, 10x – x = 7
or, 9x = 7
or, x = 7/9

$latex y=0.\overline{8}$=0.8888…

10y = 8.888
Now,
10y – y = 8
or, 9y = 8
or, y = 8/9

Therefore,

= 7/9 + 8/9
= 15/9
= 5/3 (Expressed in the form p/q where q≠0.)

3. Simplify:

(i) (64)^-2/3/(343)^-1/3

Answer:

(64)^-2/3
= (4³ )^-2/3
= 4^{3 × (-2)/3}
= 4^-2
= 1/16

(343)^-1/3
= (7³)^-1/3
= 7^{3 × (-1)/3}
= 7^-1
= 1/7

(64)^-2/3/(343)^-1/3

= 1/16 ÷ 1/7
= 1/16 × 7/1
= 7/16 (Answer)

(D) Fill in the Blanks:

(a) Between any two rational numbers there lies ________ irrational numbers.

(b) The number 0 is an example of a ________ number on the number line.

(c) An ________number cannot be expressed as a ratio of two integers.

(d) The decimal representation of the rational number 1/7 is ____________ repeating.

(e) The square of an irrational number is _________.

Answers:

(a) Between any two rational numbers there lies infinite irrational numbers.

(b) The number 0 is an example of a whole number on the number line.

(c) An irrational number cannot be expressed as a ratio of two integers.

(d) The decimal representation of the rational number 1/7 is non-terminating repeating.

(e) The square of an irrational number is irrational.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 9 Mathematics Chapter 1 Number Systems: