Solutions to NCERT Class 9 Mathematics Chapter 2 Polynomials:

Hello students and welcome to Chapter 2! We have posted top-quality solutions to all textbook exercises along with a plethora of extra questions, to help you prepare. The problems will test your understanding of the topics and give you excellent practice. We have covered the whole topic in detail and only suggest that you practise the problems on your own as well, while looking at the solutions. This will boost your speed and confidence and you will be able to solve problems faster! Good luck!

Solutions to Exercise 2.1 (Page 29) of NCERT Class 9 Mathematics Chapter 2 Polynomials:

1. Which of the following expressions are polynomials in one variable, and which are not? State reasons for your answer.

(i) 4x² – 3x + 7
(ii) y² + √2
(iii) 3√t + t√2
(iv) y + 2/y
(v) x¹⁰ + y³ + t⁵⁰

Answers:

(i) 4x² – 3x + 7
The polynomial contains only one variable x.
Therefore, 4x² – 3x + 7 is a polynomial in one variable.

(ii) y² + √2
The polynomial contains only one variable y.
Therefore, y² + √2 is a polynomial in one variable.

(iii) 3√t + t√2
The power of the variable t in the first term is 1/2 which is not a whole number. Hence, 3√t + t√2 is not a polynomial.

(iv) y + 2/y
y + 2/y = y + 2y^-1. The power of the variable y in the second term in -1, which is not a whole number. Hence, y + 2/y is not a polynomial.

(v) x¹⁰ + y³ + t⁵⁰
In the above polynomial, there are three variables x, y, t. Hence, it is not a polynomial in one variable.

Summary: (i) 4x² – 3x + 7 and (ii) y² + √2 are polynomials in one variable, while (iii) 3√t + t√2, (iv) y + 2/y, (v) x¹⁰ + y³ + t⁵⁰ are not polynomials in one variable.

2. Write the coefficients of x² in each of the following:

(i) 2 + x² + x
(ii) 2 – x² + x³
(iii) (π/2)x² + x
(iv) √2x – 1

Answers:

(i) 2 + x² + x

2 + x2 + x = 2 + (1)x2 + x
Therefore, the coefficient of x2 is 1.

(ii) 2 – x² + x³

2 – x² + x³ = 2 + (-1)x² + x³
Therefore, the coefficient of x² is (-1).

(iii) (π/2)x² + x

The coefficient of x² is π/2.

(iv) √2x – 1

√2x – 1 can be written as (0)x² + √2x – 1.
Therefore, the coefficient of x² is 0.

Summary:
The coefficients of x² in the expressions (i) 2 + x²+ x, (ii) 2 – x² + x³, (iii) (π/2) x² + x, and (iv) √2x – 1 are 1, -1, π/2, and 0 respectively.

3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.

Answer:

An example of a binomial of degree 35 is x³⁵ + 5 and an example of a monomial of degree 100 is 5x¹⁰⁰.

4. Write the degree of each of the following polynomials:

(i) 5x³ + 4x² + 7x        
(ii) 4–y²      
(iii) 5t – √7                 
(iv) 3

Answer:

(i) 5x³ + 4x² + 7x  

Degree of a polynomial refers to the highest power of the variable in the polynomial. Therefore, the degree of 5x³ + 4x² + 7x is 3.

(ii) 4 – y²      

Degree of a polynomial refers to the highest power of the variable in the polynomial. Therefore, the degree of 4 – y² is 2.

(iii) 5t – √7   

Degree of a polynomial refers to the highest power of the variable in the polynomial. Therefore, the degree of 5t – √7 is 1.

(iv) 3

Degree of a polynomial refers to the highest power of the variable in the polynomial. We can write 3 = 3x⁰. Therefore, the degree of 3 = 3x⁰ = 0.

Summary: The degree of the polynomials (i) 5x³ + 4x² + 7x, (ii) 4 − y², (iii) 5t − √7, and (iv) 3 are 3, 2, 1, and 0 respectively

5. Classify the following as linear, quadratic and cubic polynomials:

(i) x² + x              
(ii) x – x³           
(iii) y + y² + 4           
(iv) 1 + x
(v) 3t                  
(vi) r²                
(vii) 7x³

Answers:

(i) x² + x

The degree of x² + x is 2. Hence, it is quadratic polynomial.

(ii) x – x³           

The degree of x – x³ is 3. Hence, it is a cubic polynomial.

(iii) y + y² + 4

The degree of y + y² + 4 is 2. Hence, it is a quadratic polynomial.

(iv) 1 + x

The degree of 1 + x is 1. Hence, it is a linear polynomial.

(v) 3t

The degree of 3t is 1. Hence, it is a linear polynomial.

(vi) r²

The degree of r² is 2. Hence, it is quadratic polynomial.

(vii) 7x³

The degree of 7x³ is 3. Hence, it is a cubic polynomial.

Summary: (iv) 1 + x and (v) 3t are linear polynomials, (i) x² + x, (iii) y + y² + 4, (vi) r² are quadratic polynomials and (ii) x – x³and (vii) 7x³ are cubic polynomials.

Solutions to Exercise 2.2 (Page 31) of NCERT Class 9 Mathematics Chapter 2 Polynomials:

1. Find the value of the polynomial 5x − 4x² + 3 at

(i) x = 0              
(ii) x = – 1           
(iii) x = 2

Answers:

(i) x = 0

Let p(x) = 5x − 4x² + 3

or, p(0) = 5(0) – 4(0)² + 3 = 0 – 0 + 3 = 3

(ii) x = – 1

Let p(x) = 5x − 4x² + 3

or, p(-1) = 5(-1) – 4(-1)² + 3 = – 5 – 4 + 3 = – 6

(iii) x = 2

Let p(x) = 5x − 4x² + 3

or, p(2) = 5(2) – 4(2)² + 3 = 10 – 16 + 3 = – 3

Summary: The values of the polynomial 5x − 4x² + 3 at (i) x = 0, (ii) x = – 1 and (iii) x = 2 are 3, – 6, -3 respectively.

2. Find p(0), p(1) and p(2) for each of the following polynomials:

(i) p(y) = y² – y + 1           
(ii) p(t) = 2 + t + 2t² – t³
(iii) p(x) = x³                     
(iv) p(x) = (x – 1)(x + 1)

Answers:

(i) p(y) = y² – y + 1           

p(0) = 0² – 0 + 1 = 1

p(1) = 1² – 1 + 1 = 1

p(2) = 2² – 2 + 1 = 3

(ii) p(t) = 2 + t + 2t² – t³

p(0) = 2 + 0 + 2(0)² – (0)³ = 2

p(1) = 2 + 1 + 2(1)² – (1)³ = 2 + 1 + 2 – 1 = 4

p(2) = 2 + 2 + 2(2)² – (2)³ = 2 + 2 + 8 – 8 = 4

(iii) p(x) = x³

p(0) = (0)³ = 0

p(1) = 1³ = 1

p(2) = 2³ = 8

(iv) p(x) = (x – 1)(x + 1)

p(0) = (0 – 1)(0 + 1) = (-1)(1) = – 1

p(1) = (1 – 1)(1 + 1) = (0)(2) = 0

p(2) = (2 – 1)(2 + 1) = (1)(3) = 3

Summary:

The values of p(0), p(1) and p(2) for (i) p(y) = y² – y + 1, (ii)p(t) = 2 + t + 2t² – t³, (iii) p(x) = x³ and (iv) p(x) = (x – 1)(x + 1) are (1, 1, 3), (2, 4, 4), (0, 1, 8) and (-1, 0, 3).

3. Verify whether the following are zeroes of the polynomial, indicated against them.

(i) p(x) = 3x + 1, x = −1/3
(ii) p(x) = 5x – π, x = 4/5
(iii) p(x) = x²−1, x = 1, −1
(iv) p(x) = (x + 1)(x – 2), x =−1, 2
(v) p(x) = x², x = 0
(vi) p(x) = lx + m, x = −m/l
(vii) p(x) = 3x² − 1, x = – 1/√3 , 2/√3
(viii) p(x) = 2x + 1, x = 1/2

Answers:

(i) p(x) = 3x + 1, x = −1/3

p(−1/3) = 3(−1/3) + 1 = – 1 + 1 = 0
Therefore, x = −1/3 is a zero of the polynomial p(x) = 3x + 1.

(ii) p(x) = 5x – π, x = 4/5

p(4/5) = 5(4/5) – π = 4 – π ≠ 0
Therefore, x = 4/5 is not a zero of the polynomial p(x) = 5x – π.

(iii) p(x) = x²−1, x = 1, −1

p(1) = 12 – 1 = 0
p(-1) = (-1)2 – 1 = 1 – 1 = 0
Therefore, x = 1, – 1 are both zeroes of the polynomial p(x) = x2−1.

(iv) p(x) = (x + 1)(x – 2), x =−1, 2

p(-1) = (-1 + 1)(-1 – 2) = (0)(-3) = 0
p(2) = (2 + 1)(2 – 2) = 3(0) = 0
Therefore, x =−1, 2 are both zeroes of the polynomial p(x) = (x + 1)(x – 2).

(v) p(x) = x², x = 0

p(0) = (0)² = 0
Therefore, x = 0 is a zero of the polynomial p(x) = x2.

(vi) p(x) = lx + m, x = −m/l

p(−m/l) = l(−m/l) + m = -m + m = 0
Therefore, x = −m/l is a zero of the polynomial p(x) = lx + m.

(vii) p(x) = 3x² − 1, x = – 1/√3 , 2/√3

p(-1/√3) = 3(-1/√3)² – 1 = 3(1/3) – 1 = 1 – 1 = 0
p(2/√3) = 3(2/√3)² – 1 = 3(4/3) – 1 = 4 – 1 = 3
Therefore, x = – 1/√3 is a zero of the polynomial p(x) = 3x² – 1, but x = 2/√3 is not a zero of p(x) = 3x² – 1.

(viii) p(x) = 2x + 1, x = 1/2

p(1/2) = 2(1/2) + 1 = 1 + 1 = 2
Therefore, x = 1/2 is not a zero of the polynomial p(x) = 2x + 1.

4. Find the zero of the polynomial in each of the following cases:

(i) p(x) = x + 5               
(ii) p(x) = x – 5               
(iii) p(x) = 2x + 5
(iv) p(x) = 3x – 2         
(v) p(x) = 3x                     
(vi) p(x) = ax, a≠0
(vii) p(x) = cx + d, c ≠ 0, c, d are real numbers.

Answers:

(i) p(x) = x + 5

p(x) = x + 5 = 0

or, x = – 5

Therefore, x = – 5 is a zero of the polynomial p(x) = x + 5.

(ii) p(x) = x – 5

p(x) = x – 5 = 0

or, x = 5

Therefore, x = 5 is a zero of the polynomial p(x) = x – 5.

(iii) p(x) = 2x + 5

p(x) = 2x + 5 = 0

or, 2x = – 5

or, x = -5/2

Therefore, x = -5/2 is a zero of the polynomial p(x) = 2x + 5.

(iv) p(x) = 3x – 2

p(x) = 3x – 2 = 0

or, 3x = 2

or, x = 2/3

Therefore, x = 2/3 is a zero of the polynomial p(x) = 3x – 2.

(v) p(x) = 3x

p(x) = 3x = 0

or, x = 0

Therefore, x = 0 is a zero of the polynomial p(x) = 3x.

(vi) p(x) = ax, a≠0

p(x) = ax = 0

or x = 0

Therefore, x = 0 is a zero of the polynomial p(x) = ax, a≠0.

(vii) p(x) = cx + d, c ≠ 0, c, d are real numbers.

p(x) = cx + d = 0

or, cx = -d

or, x = -d/c 

Therefore, x = -d/c is a zero of the polynomial p(x) = cx + d.

Summary:

The zeros of the polynomials in each of the following cases (i) p(x) = x + 5, (ii) p(x) = x – 5, (iii) p(x) = 2x + 5, (iv) p(x) = 3x – 2, (v) p(x) = 3x, (vi) p(x) = ax, (a ≠ 0), and (vii) p(x) = cx + d, (c ≠ 0 and c, d are real numbers) are -5, 5, -5/2, 2/3, 0, 0, and -d/c respectively.

Solutions to Exercise 2.3 (Page 35) of NCERT Class 9 Mathematics Chapter 2 Polynomials:

1. Determine which of the following polynomials has (x + 1) a factor:

(i) x³ + x² + x + 1                                   
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1                    
(iv) x³ – x²– (2 + √2)x + √2

Answer:

(i) x³ + x² + x + 1

x + 1 = 0

or, x = – 1

p(-1) = (-1)³ + (-1)² – 1 + 1 = – 1 + 1 – 1 + 1 = 0

Since p(-1) = 0, x + 1 is a factor of x³ + x² + x + 1.

(ii) x⁴ + x³ + x² + x + 1

x + 1 = 0

or, x = – 1

p(-1) = (-1)⁴ + (-1)³ + (-1)² – 1 + 1 = 1 – 1 + 1 – 1 + 1 = 1 ≠ 0.

Since p(-1) = 1 ≠ 0, x + 1 is a not factor of x⁴ + x³ + x² + x + 1.

(iii) x⁴ + 3x³ + 3x² + x + 1

x + 1 = 0

or, x = – 1

p(-1) = (-1)⁴ + 3(-1)³ + 3(-1)² – 1 + 1 = 1 – 3 + 3 – 1 + 1 = 1 ≠ 0.

Since p(-1) = 1 ≠ 0, x + 1 is a not factor of x⁴ + 3x³ + 3x² + x + 1.

(iv) x³ – x²– (2 + √2)x + √2

x + 1 = 0

or, x = – 1

p(-1) = (-1)³ – (-1)² – (2 + √2)(-1) + √2

= -1 – 1 + 2 + √2 + √2

= 2√2 ≠ 0 Since p(-1) = 2√2 ≠ 0, x + 1 is a not factor of x³ – x²– (2 + √2)x + √2.

2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:

(i) p(x) = 2x³ + x² – 2x – 1, g(x) = x + 1

(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2

(iii) p(x) = x³ – 4x² + x + 6, g(x) = x – 3

Answers:

(i) p(x) = 2x³ + x² – 2x – 1, g(x) = x + 1

By Factor Theorem, x – a is a factor of p(x), if p(a) = 0.

g(x) = x + 1 = 0

or, x = – 1

p(−1) = 2(−1)³ + (−1)² – 2(−1) – 1

= −2 + 1 + 2 − 1

= 0

Since p(−1) = 0, g(x) = x + 1 is a factor of p(x) = 2x³ + x² – 2x – 1.

(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2

g(x) = x + 2 = 0

or, x = – 2

p(-2) = (-2)³ + 3(-2)² + 3(-2) + 1

= – 8 + 12 – 6 + 1

= – 1 ≠ 0

Since, p(-2) ≠ 0, by Factor Theorem we can say that g(x) = x + 2 is not a factor of p(x) = x³ + 3x² + 3x + 1.

(iii) p(x) = x³ – 4x² + x + 6, g(x) = x – 3

g(x) = x – 3 = 0

or, x = 3

p(3) = (3)³ – 4(3)² + 3 + 6

= 27 – 36 + 3 + 6

= 0

Since p(3) = 0, by Factor Theorem we can say that g(x) = x – 3 is factor of p(x) = x³ – 4x² + x + 6.

Summary: Using factor theorem we determine that (i) g(x) = x + 1 is a factor of p(x) = 2x³ + x² – 2x – 1, (ii) g(x) = x + 2 is not a factor of p(x) = x³ + 3x² + 3x + 1, and (iii) g(x) = x – 3 is a factor of p(x) = x³ – 4x² + x + 6.

3. Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:

(i) p(x) = x² + x + k                       
(ii) p(x) = 2x² + kx + √2
(iii) p(x) = kx² – √2x + 1             
(iv) p(x) = kx² – 3x + k

Answers:

(i) p(x) = x² + x + k

By Factor Theorem, if x – 1 is a factor of p(x) = x² + x + k, then p(1) = 0.

p(1) = 1² + 1 + k = 0

or, k = -2

(ii) p(x) = 2x² + kx + √2

By Factor Theorem, if x – 1 is a factor of p(x) = 2x² + kx + √2, then p(1) = 0.

p(1) = 2(1)² + k(1) + √2 = 0

or, 2 + k + √2 = 0

or, k = – 2 – √2

(iii) p(x) = kx² – √2x + 1

By Factor Theorem, if x – 1 is a factor of p(x) = kx² – √2x + 1, then p(1) = 0.

p(1) = k(1)² – √2(1) + 1 = 0

or, k – √2 + 1 = 0

or, k = √2 – 1

(iv) p(x) = kx² – 3x + k

By Factor Theorem, if x – 1 is a factor of p(x) = kx² – 3x + k, then p(1) = 0.

p(1) = k(1)² – 3(1) + k = 0

or, k – 3 + k = 0

or, 2k = 3

or, k = 3/2

Summary: The values of k, if (x – 1) is a factor of p(x) in each of the following cases (i) p(x) = x² + x + k, (ii) p(x) = 2x² + kx + √2, (iii) p(x) = kx² – √2x + 1, (iv) p(x) = kx² – 3x + k are -2, – 2 – √2, √2 – 1, and 3/2 respectively.

4. Factorise:

(i) 12x² – 7x + 1                    
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6                     
(iv) 3x² – x – 4

Answers:

(i) 12x² – 7x + 1

p + q = -7 and pq = 12 × 1 = 12

We get -3 and -4 as the numbers because – 3 – 4 = -7 and (-3)(-4) = 12.

12x² – 7x + 1

= 12x² + (-3 – 4)x + 1

= 12x² – 3x – 4x + 1

= 3x(4x – 1) – 1(4x – 1)

= (4x – 1)(3x – 1)

(ii) 2x² + 7x + 3

p + q = 7 and pq = 2 × 3 = 6

We get 6 and 1 as the numbers because 6 + 1 = 7 and (6)(1) = 6.

2x² + 7x + 3

= 2x² + (6 + 1)x + 3

= 2x² + 6x + x + 3

= 2x(x + 3) + 1(x + 3)

= (x + 3)(2x + 1)

(iii) 6x² + 5x – 6

p + q = 5 and pq = 6 × (-6) = -36

We get 9 and -4 as the numbers because 9 – 4 = 5 and (9)(-4) = -36.

6x² + 5x – 6

= 6x² + (9 – 4)x – 6

= 6x² + 9x – 4x – 6

= 3x(2x + 3) – 2(2x + 3)

= (2x + 3)(3x – 2)

(iv) 3x² – x – 4

p + q = -1 and pq = 3 × (-4) = -12

We get -4 and 3 as the numbers because -4 + 3 = -1 and (-4)(3) = -12.

3x² – x – 4

= 3x² + (-4 + 3)x – 4

= 3x² – 4x + 3x – 4

= x(3x – 4) + 1(3x – 4)

= (3x – 4)(x + 1)

Summary: The factorized form of (i) 12x² – 7x + 1, (ii) 2x² + 7x + 3, (iii) 6x² + 5x – 6 and (iv) 3x² – x – 4 are (4x – 1)(3x – 1), (x + 3)(2x + 1), (2x + 3)(3x – 2), (3x – 4)(x + 1) respectively.

5. Factorise:

(i) x³ – 2x² – x + 2                               
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20                   
(iv) 2y³ + y² – 2y – 1
(i) x³ – 2x² – x + 2                         

Answers:

(i) x³ – 2x² – x + 2   

Let p(x) = x³ – 2x² – x + 2

Factors of 2 are ±1 and ± 2.

p(1) = (1)³ – 2(1)² – (1) + 2

= 1 – 2 – 1 + 2

= 0

Therefore, by factor theorem (x – 1) is a factor of p(x).

Now we divide p(x) by (x – 1):

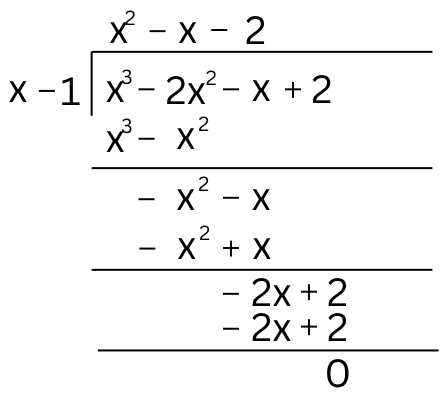
x³ – 2x² – x + 2 = (x – 1)(x² – x – 2)

Now, x² – x – 2 can be factorised by splitting the middle term.

p + q = -1 and pq = (1)(-2) = -2

We get -2 and 1 as the numbers because -2 + 1 = -1 and (-2)(1) = -2.

x² – x – 2

= x² + (-2 + 1)x – 2

= x² – 2x + x – 2

= x(x – 2) + 1(x – 2)

= (x – 2)(x + 1)

x³ – 2x² – x + 2 = (x – 1)(x – 2)(x + 1)

(ii) x³ – 3x² – 9x – 5

p(x) = x³ – 3x² – 9x – 5

We observe,

p(-1) = (-1)³ – 3(-1)² – 9(-1) – 5 = – 1 – 3 + 9 – 5 = 0

By factor theorem, x + 1 is a factor of p(x).

Now we see that,

x³ – 3x² – 9x – 5

= x³ + x² – 4x² – 4x – 5x – 5

= x²(x + 1) – 4x(x + 1) – 5(x + 1)

= (x + 1)(x² – 4x – 5)

Now, x² – 4x – 5 can be factorised by splitting the middle term.

p + q = -4 and pq = (1)(-5) = -5

We get -5 and 1 as the numbers because -5 + 1 = -4 and (-5)(1) = -5.

x² – 4x – 5

= x² + (-5 + 1)x – 5

= x² – 5x + x – 5

= x(x – 5) + 1(x – 5)

= (x – 5)(x + 1)

x³ – 3x² – 9x – 5 = (x + 1)(x – 5)(x + 1)

(iii) x³ + 13x² + 32x + 20

p(x) = x³ + 13x² + 32x + 20

We observe,

p(-1) = (-1)³ + 13(-1)² + 32(-1) + 20 = – 1 + 13 – 32 + 20 = 0

By factor theorem, x + 1 is a factor of p(x).

Now we see that,

x³ + 13x² + 32x + 20

= x³ + x² + 12x² + 12x + 20x + 20

= x²(x + 1) + 12x(x + 1) + 20(x + 1)

= (x + 1)(x² + 12x + 20)

Now, x² + 12x + 20 can be factorised by splitting the middle term.

p + q = 12 and pq = (20)(1) = 20

We get 10 and 2 as the numbers because 10 + 2 = 12 and (10)(2) = 20.

x² + 12x + 20

= x² + (10 + 2)x + 20

= x² + 10x + 2x + 20

= x(x + 10) + 2(x + 10)

= (x + 10)(x + 2)

x³ + 13x² + 32x + 20 = (x + 1)(x + 10)(x + 2)

(iv) 2y³ + y² – 2y – 1

p(y) = 2y³ + y² – 2y – 1

We observe,

p(1) = 2(1)³ + (1)² – 2(1) – 1 = 2 + 1 –  2 – 1 = 0

By factor theorem, y – 1 is a factor of p(y).

Now we divide p(y) by (y – 1):

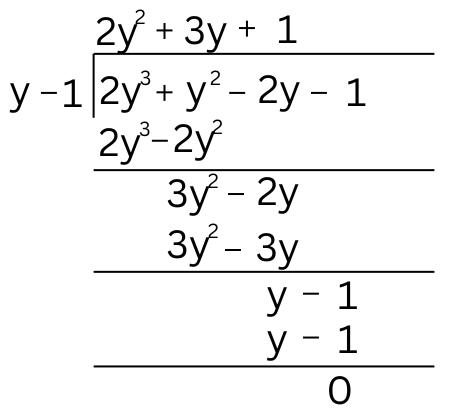
2y³ + y² – 2y – 1 = (y – 1)(2y² + 3y + 1)

Now, 2y² + 3y + 1 can be factorised by splitting the middle term.

p + q = 3 and pq = (2)(1) = 2

We get 2 and 1 as the numbers because 2 + 1 = 3 and (2)(1) = 2.

2y² + 3y + 1

= 2y² + (2 + 1)y + 1

= 2y² + 2y + y + 1

= 2y(y + 1) + 1(y + 1)

= (y + 1)(2y + 1)

Therefore,

2y³ + y² – 2y – 1 = (y – 1)(y + 1)(2y + 1)

Summary:

The factorized form of (i) x³ – 2x² – x + 2, (ii) x³ – 3x² – 9x – 5, (iii) x³ + 13x² + 32x + 20 and (iv) 2y³ + y² – 2y – 1 are (x – 1)(x – 2)(x + 1), (x + 1)(x – 5)(x + 1), (x + 1)(x + 10)(x + 2)and (y – 1)(y + 1)(2y + 1) respectively.

Solutions to Exercise 2.4 (Page 40) of NCERT Class 9 Mathematics Chapter 2 Polynomials:

1. Use suitable identities to find the following products:

(i) (x + 4)(x + 10)            
(ii) (x + 8)(x – 10)            
(iii) (3x + 4)(3x – 5)
(iv) (y² + 3/2)(y² – 3/2)          
(v) (3 – 2x)(3 + 2x)

Answers:

(i) (x + 4)(x + 10)            

Using the identity (x + a)(x + b) = x² + (a + b)x + ab we get:

(x + 4)(x + 10) = x² + (4 + 10)x + 4 × 10 = x² + 14x + 40

(ii) (x + 8)(x – 10)

Using the identity (x + a)(x + b) = x² + (a + b)x + ab we get:

(x + 8)(x – 10) = x² + (8 – 10)x + 8 × (-10) = x² – 2x – 80

(iii) (3x + 4)(3x – 5)

Using the identity (x + a)(x + b) = x² + (a + b)x + ab we get:

(3x + 4)(3x – 5) = (3x)² + [4 + (-5)]3x + (4)(-5) [Taking 3x in place of x]

= 9x² – 3x – 20

(iv) (y² + 3/2)(y² – 3/2)

Using identity (a + b)(a – b) = a² – b² we get:

(y² + 3/2)(y² – 3/2) = (y²)² – (3/2)² [Taking a = y² and b = ]

= y⁴ – 9/4

(v) (3 – 2x)(3 + 2x)

Using identity (a – b)(a + b) = a² – b² we get:

(3 – 2x)(3 + 2x) = 3² – (2x)² [Taking a = 3 and b = 2x]

= 9 – 4x²

Summary: Using suitable identities we find the products of (i) (x + 4)(x + 10), (ii) (x + 8)(x – 10), (iii) (3x + 4)(3x – 5), (iv) (y² + 3/2)(y² – 3/2), and (v) (3 – 2x)(3 + 2x) as x² + 14x + 40, x² – 2x – 80, 9x² – 3x – 20, y⁴ – 9/4, and 9 – 4x² respectively.

2. Evaluate the following products without multiplying directly:

(i) 103 × 107               
(ii) 95 × 96               
(iii) 104 × 96

Answers:

(i) 103 × 107

103 × 107 = (100 + 3) × (100 + 7)

We use the identity [(x + a)(x + b) = x² + (a + b)x + ab].

Here, x = 100, a = 3, b = 7

Now, 103 × 107 = (100 + 3) × (100 + 7)

= (100)² + (3 + 7)100 + (3 × 7)

= 10000 + 1000 + 21

= 11021

(ii) 95 × 96

95 × 96 = (100 – 5)(100 – 4)

We use the identity [(x + a)(x + b) = x² + (a + b)x + ab].

Here, x = 100, a = -5, b = -4

Now, 95 × 96 = (100 – 5) × (100 – 4)

(100)² + (-5 + (-4))100 + (-5) × (-4)

= 10000 – 900 + 20

= 9120

(iii) 104 × 96

104 × 96 = (100 + 4) × (100 – 4)

We use the identity [(a + b)(a – b)= a² – b²]

Here, a = 100, b = 4

Now, 104 × 96 = (100 + 4) × (100 – 4)

= (100)² – (4)²

= 10000 – 16

= 9984

Summary: The products without multiplying directly of (i)103 × 107, (ii)95 × 96 and (iii) 104 × 96 are 11021, 9120 and 9984 respectively.

3. Factorise the following using appropriate identities:

(i) 9x² + 6xy + y²                             
(ii) 4y² − 4y + 1                 
(iii)  x² – y²/100

Answers:

(i) 9x² + 6xy + y²

We use identity x² + 2xy + y² = (x + y)².

Here, x = 3x and y = y.

Therefore,

9x² + 6xy + y²

= (3x)² + 2(3x)(y) + y²

= (3x + y)²

(ii) 4y² − 4y + 1

We use identity x² – 2xy + y² = (x – y)².

Here, x = 2y and y = 1.

Therefore,

4y² − 4y + 1

= (2y)² – 2(2y)(1) + 1²

= (2y – 1)²

(iii)  x² – y²/100       

We use the identity [(a + b)(a – b)= a² – b²]

Here, a = x, b = y/10

Therefore,

x² – y²/100      

= (x)² – (y/10)²

= (x + y/10)(x – y/10)

Summary: The factorized form using appropriate identities of (i) 9x² + 6xy + y², (ii) 4y² – 4y + 1, and (iii) x² – y²/100 are (3x + y)², (2y – 1)², and (x + y/10) (x – y/10) respectively.

4. Expand each of the following using suitable identities:

(i) (x + 2y + 4z)²                
(ii) (2x – y + z)²                 
(iii) (−2x + 3y + 2z)²
(iv) (3a – 7b – c)²            
(v) (–2x + 5y – 3z)²          
(vi) [(1/4)a – (1/2)b + 1]²

Answers:

(i) (x + 2y + 4z)²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = x

y = 2y

z = 4z

(x + 2y + 4z)² = x² + (2y)² + (4z)² +( 2 × x × 2y) + (2 × 2y × 4z) + (2 × 4z × x)

= x² + 4y² + 16z² + 4xy + 16yz + 8xz

(ii) (2x – y + z)²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = 2x

y = -y

z = z

(2x – y + z)² = (2x)² + (-y)² + z² + 2 × 2x × (-y) + 2 × (-y) × z + 2 × z × 2x

= 4x² + y² +z ² – 4xy – 2yz + 4xz

(iii) (−2x + 3y + 2z)²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = -2x

y = 3y

z = 2z

(−2x + 3y + 2z)² = (-2x)² + (3y)² + (2z)² + 2 × (-2x) × (3y) + 2 × (3y) × (2z) + 2 × (2z) × (-2x)

= 4x² + 9y² + 4z² – 12xy + 12yz – 8xz

(iv) (3a – 7b – c)²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = 3a

y = -7b

z = -c

(3a – 7b – c)² = (3a)² + (-7b)² + (-c)² + 2 × (3a) × (-7b) + 2 × (-7b) × (-c) + 2 × (-c) × (3a)

= 9a² + 49b² + c²– 42ab + 14bc – 6ca

(v) (–2x + 5y – 3z)²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = -2x

y = 5y

z = -3z

(–2x + 5y – 3z)² = (–2x)² + (5y)² + (–3z)² + 2 × (-2x) × (5y) + 2 × (5y) × (-3z) + 2 × (-3z) × (-2x)

= 4x² + 25y² + 9z² – 20xy – 30yz + 12zx

(vi) [(1/4)a – (1/2)b + 1]²

We use the identity (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Here, x = a/4

y = – b/2

z = 1

[(1/4)a – (1/2)b + 1]² = (a/4)² + (– b/2)² + 1² + 2 × (a/4) × (– b/2) + 2 × (– b/2) × 1 + 2 × (1) × (a/4)

= (1/16)a² + (1/4)b² + 1 – ab/4 – b + a/2

Summary: The expanded form of each of the following (i) (x + 2y + 4z)², (ii) (2x – y + z)², (iii) (−2x + 3y + 2z)², (iv) (3a – 7b – c)², (v) (–2x + 5y – 3z)² and (vi) [a – b + 1]² are x² + 4y² + 16z² + 4xy + 16yz + 8xz, 4x² + y² +z ² – 4xy – 2yz + 4xz, 4x² + 9y² + 4z² – 12xy + 12yz – 8xz, 9a² + 49b² + c²– 42ab + 14bc – 6ca, 4x² + 25y² + 9z² – 20xy – 30yz + 12zx, (1/16)a² + (1/4)b² + 1 – ab/4 – b + a/2 respectively.

5. Factorise:

(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz

(ii) 2x² + y² + 8z² –2√2xy + 4√2yz – 8xz

Answers:

(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz

We use the identity x² + y² + z² + 2xy + 2yz + 2zx = (x + y + z)².

4x² + 9y² + 16z² + 12xy – 24yz – 16xz

= (2x)² + (3y)² + (-4z)² + 2(2x)(3y) + 2(3y)(-4z) + 2(2x)(-4z)

Here x = 2x, y = 3y and z = -4z.

= (2x + 3y – 4z)²

(ii) 2x² + y² + 8z² –2√2xy + 4√2yz – 8xz

We use the identity x² + y² + z² + 2xy + 2yz + 2zx = (x + y + z)².

2x² + y² + 8z² –2√2xy + 4√2yz – 8xz

= (-√2x)² + y² + (2√2z)² + 2(-√2x)(y) + 2(y)( 2√2z) + 2(2√2z)(-√2x)

Here, x = -√2x, y = y and z = 2√2z.

= (-√2x + y + 2√2z)²

Summary: The factorised forms of (i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz and (ii) 2x² + y² + 8z² –2√2xy + 4√2yz – 8xz are (2x + 3y – 4z)² and (-√2x + y + 2√2z)² respectively.

6. Write the following cubes in expanded form:

(i) (2x + 1)³            
(ii) (2a − 3b)³          
(iii) [(3/2)x + 1]³               
(iv) [x – (2/3)y]³

Answers:

(i) (2x + 1)³

We use the identity (x + y)³ = x³ + y³ + 3xy(x + y):

Here x = 2x and y = 1.

(2x + 1)³= (2x)³ + 1³ + 3 × 2x × 1(2x + 1)

= 8x³ + 1 + 6x(2x + 1)

= 8x³ + 12x² + 6x + 1

(ii) (2a − 3b)³

We use the identity (x – y)³ = x³ – y³ – 3xy(x – y):

Here x = 2a and y = 3b.

(2a − 3b)³ = (2a)³ – (3b)³ – 3(2a)(3b)(2a – 3b)

= 8a³ – 27b³ – 18ab(2a – 3b)

= 8a³ – 27b³ – 36a²b + 54ab²

(iii) [(3/2)x + 1]³

We use the identity (x + y)³ = x³ + y³ + 3xy(x + y):

Here x = (3/2)x and y = 1.

[(3/2)x + 1]³ = ((3/2)x)³ + 1³ + 3.(3/2).x.1.((3/2)x + 1)

= (27/8)x³ + 1 + (9/2)x ((3/2)x + 1)

= (27/8)x³ + 1 + (27/4)x² + (9/2)x

= (27/8)x³ + (27/4)x² + (9/2)x + 1

(iv) [x – (2/3)y]³

We use the identity (x – y)³ = x³ – y³ – 3xy(x – y):

Here x = x and y = (2/3)y.

[x – (2/3)y]³ = x³ – ((2/3)y)³ – 3x((2/3)y)(x – (2/3)y)

= x³ – (8/27)y³ – 2xy(x – (2/3)y)

= x³ – (8/27)y³ – 2x²y + (4/3)xy²

Summary: The expanded forms of the following cubes (i) (2x + 1)³, (ii) (2a − 3b)³, (iii) [(3/2)x + 1]³ , (iv) [x – (2/3)y]³ are 8x³ + 12x² + 6x + 1, 8a³ – 27b³ – 36a²b + 54ab², (27/8)x³ + (27/4)x² + (9/2)x + 1, x³ – (8/27)y³ – 2x²y + (4/3)xy² .

7. Evaluate the following using suitable identities: 

(i) (99)³                      
(ii) (102)³                   
(iii) (998)³

Answers:

(i) (99)³

99 = 100–1

We use identity (x – y)³ = x³ – y³ – 3xy(x – y):

(99)³ = (100 – 1)³

= (100)³ – 1³ – (3 × 100 × 1)(100 – 1)

= 1000000 – 1 – 300(100 – 1)

= 1000000 – 1 – 30000 + 300

= 970299

(ii) (102)³

102 = 100 + 2

We use identity (x + y)³ = x³ + y³ + 3xy(x + y):

(100 + 2)³ = (100)³ + 2³ + (3 × 100 × 2)(100 + 2)

= 1000000 + 8 + 600(100 + 2)

= 1000000 + 8 + 60000 + 1200

= 1061208

(iii) (998)³

998 = 1000 – 2

We use identity (x – y)³ = x³ – y³ – 3xy(x – y):

(998)³ = (1000 – 2)³

= (1000)³ – (2)³ – 3(1000) (2) (1000 – 2)

= 1000000000 – 8 – 6000(1000 – 2)

= 1000000000 – 8 – 6000000 + 12000

= 994011992

Summary: The evaluated values using suitable identities of the following (i) (99)³, (ii) (102)³, and (iii) (998)³ are 970299, 1061208, and 994011992 respectively.

8. Factorise each of the following:

(i) 8a³ + b³ + 12a²b + 6ab²                                 (ii) 8a³ – b³ – 12a²b + 6ab²

(iii) 27 – 125a³ – 135a + 225a²                        (iv) 64a³ – 27b³ – 144a²b + 108ab²

(v) 27p³ – 1/216 – (9/2)p² + (1/4)p

Answers:

(i) 8a³ + b³ + 12a²b + 6ab²

8a³ + b³ + 12a²b + 6ab² = (2a)³ + b³ + 3(2a)²b + 3(2a)(b)²

This is of the form x³ + y³ + 3x²y + 3xy² = (x + y)³, where x = 2a, y = b.

= (2a + b)³

(ii) 8a³ – b³ – 12a²b + 6ab²

8a³ – b³ – 12a²b + 6ab² = (2a)³ – b³ – 3(2a)²b + 3(2a)(b)²

This is of the form x³ – y³ – 3x²y + 3xy² = (x – y)³, where x = 2a, y = b.

= (2a – b)³

(iii) 27 – 125a³ – 135a + 225a² 

27 – 125a³ – 135a + 225a² = 3³ – (5a)³ – 3(3)³5a + 3(3)(5a)²

This is of the form x³ – y³ – 3x²y + 3xy² = (x – y)³, where x = 3, y = 5a.

= (3 – 5a)³

(iv) 64a³ – 27b³ – 144a²b + 108ab²

64a³ – 27b³ – 144a²b + 108ab² = (4a)³ – (3b)³ – 3(4a)²(3b) + 3(4a)(3b)²

This is of the form x³ – y³ – 3x²y + 3xy² = (x – y)³, where x = 4a, y = 3b.

= (4a – 3b)³

(v) 27p³ – 1/216 – (9/2)p² + (1/4)p

27p³ – 1/216 – (9/2)p² + (1/4)p= (3p)³ – (1/6)³ – 3(3p)² (1/6) +3(3p)(1/6)²

= (3p – 1/6)³

Summary: The factorised form of the following (i) 8a³ + b³ + 12a²b + 6ab², (ii) 8a³ – b³ – 12a²b + 6ab², (iii) 27 – 125a³ – 135a + 225a², (iv) 64a³ – 27b³ – 144a²b + 108ab², 27p³ – 1/216 – (9/2)p² + (1/4)p are (2a + b)³, (2a – b)³, (3 – 5a)³, (4a – 3b)³ and (3p – 1/6)³ respectively.

9. Verify:

(i) x³ + y³ = (x + y)(x² – xy + y²)                  (ii) x³ – y³ = (x – y)(x² + xy + y²)

Answers:

(i) x³ + y³ = (x + y)(x² – xy + y²)

We use the identity (x + y)³ = x³ + y³ + 3xy(x + y):

x³ + y³ = (x + y)³ – 3xy(x + y)

or, x³ + y³ = (x + y)[(x + y)² – 3xy]

or, x³ + y³ = (x + y)[x² + y² + 2xy – 3xy]

or, x³ + y³ = (x + y)(x² + y² – xy)

(ii) x³ – y³ = (x – y)(x² + xy + y²)

We use the identity (x – y)³ = x³ – y³ – 3xy(x – y):

x³ – y³ = (x – y)³ + 3xy(x – y)

or, x³ – y³ = (x – y)[(x – y)² + 3xy]

or, x³ – y³ = (x – y)(x² + y² – 2xy + 3xy)

or, x³ – y³ = (x – y)(x² + xy + y²)

Summary: Hence it is verified that (i) x³ + y³ = (x + y)(x² – xy + y²) and (ii) x³ – y³ = (x – y)(x² + xy + y²).

10. Factorise each of the following:

(i) 27y³ + 125z³                   (ii) 64m³ – 343n³

[Hint: See Question 9.]

Answers:

(i) 27y³ + 125z³

= (3y)³ + (5z)³

Using identity x³ + y³ = (x + y)(x² – xy + y²) we get:

(3y)³ + (5z)³ = (3y + 5z)[(3y)² – (3y)(5z) + (5z)²]

= (3y + 5z)(9y² – 15yz + 25z²)

(ii) 64m³ – 343n³

= (4m)³ – (7n)³

Using identity x³ – y³ = (x – y)(x² + xy + y²) we get:

(4m)³ – (7n)³

= (4m – 7n)[(4m)² + (4m)(7n) + (7n)²]

= (4m – 7n)(16m² + 28mn + 49n²)

Summary:

The factorised form of (i) 27y³ + 125z³ and(ii) 64m³ – 343n³ are (3y + 5z)(9y² – 15yz + 25z²) and (4m – 7n)(16m² + 28mn + 49n²) respectively.

11. Factorise: 27x³ + y³ + z³ – 9xyz. 

Answer:

27x³ + y³ + z³ – 9xyz = (3x)³ + y³ + z³ +3(3x)(y)(z)

We use the identity x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx):

(3x)³ + y³ + z³ +3(3x)(y)(z)

= (3x + y + z)[(3x)² + y² + z² – (3x)(y) – (y)(z) – (z)(3x)]

= (3x + y + z)(9x² + y² + z² – 3xy – yz – 3xz)

Summary: The factorised form of 27x³ + y³ + z³ – 9xyz is (3x + y + z)(9x² + y² + z² – 3xy – yz – 3xz).

12. Verify that x³ + y³ + z³ – 3xyz = (x + y + z)[(x – y)² + (y – z)² + (z – x)²]

Answer:

We use the identity x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx):

or, x³ + y³ + z³ – 3xyz =  (x + y + z)[2(x² + y² + z² – xy – yz – zx)]

or, x³ + y³ + z³ – 3xyz =  (x + y + z)[2x² + 2y² + 2z² – 2xy – 2yz – 2zx]

or, x³ + y³ + z³ – 3xyz =  (x + y + z)[(x² + y² − 2xy) + (y² + z² – 2yz) + (x² + z² –2xz)]

or, x³ + y³ + z³ – 3xyz = (x + y + z)[(x – y)² + (y – z)² + (z – x)²] (Proved)

Summary: Hence, it is verified that x³ + y³ + z³ – 3xyz = (x + y + z)[(x – y)² + (y – z)² + (z – x)²].

13. If x + y + z = 0, show that x³ + y³ + z³ = 3xyz.

Answer:

Answer:

We know x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)

or, x³ + y³ + z³ – 3xyz = (0) (x² + y² + z² – xy – yz – zx)

or, x³ + y³ + z³ – 3xyz = 0

or, x³ + y³ + z³ = 3xyz (Proved)

Summary: Hence it is proved that if x + y + z = 0, x³ + y³ + z³ = 3xyz.

14. Without actually calculating the cubes, find the value of each of the following:

(i) (−12)³ + (7)³ + (5)³

(ii) (28)³ + (−15)³ + (−13)³

Answer:

(i) (−12)³ + (7)³ + (5)³

Here, x = -12, y = 7 and z = 5 and x + y + z = -12 + 7 + 5 = 0.

We know that, if x + y + z = 0, x³ + y³ + z³ = 3xyz.

Therefore,

(−12)³ + (7)³ + (5)³ = 3(-12)(7)(5) = -1260

(ii) (28)³ + (−15)³ + (−13)³

Here, x = 28, y = -15 and z = -13 and x + y + z = 28 – 15 – 13 = 0.

We know that, if x + y + z = 0, x³ + y³ + z³ = 3xyz.

Therefore,

(28)³ + (-15)³ + (-13)³ = 3(28)(-15)(-13) = 16380

Summary: Without actually calculating the cubes the values of (i) (−12)³ + (7)³ + (5)³ and (ii) (28)³ + (−15)³ + (−13)³ are -1260 and 16380.

15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given: 

(i) Area: 25a² – 35a + 12

(ii) Area: 35y² + 13y – 12

Answers:

(i) Area: 25a² – 35a + 12

Area = Length × Breadth

Therefore, we have to factorise the expression for area.

p + q = -35 and pq = 25 × 12 = 300

By trial and error, we get p = -20 and q = -15.

25a² – 35a + 12

= 25a² – 20a – 15a + 12

= 5a(5a – 4) – 3(5a – 4)

= (5a – 3)(5a – 4)

Therefore, length = 5a – 3 and breath = 5a – 4.

(ii) Area: 35y² + 13y – 12

Area = Length × Breadth

Therefore, we have to factorise the expression for area.

p + q = 13 and pq = 35 × (-12) = -420

By trial and error we get p = -15 and q = 28.

35y² + 13y – 12

= 35y² – 15y + 28y – 12

= 5y(7y – 3) + 4(7y – 3)

= (5y + 4)(7y – 3)

Therefore, length = 5y + 4 and breadth = 7y – 3.

Summary: The possible expressions for the length and breadth of each of the following rectangles of (i) Area: 25a² – 35a + 12 and (ii) Area: 35y² + 13y – 12 are (Length = 5a – 3, Breadth = 5a – 4) and (Length = 5y + 4, Breadth = 7y – 3) respectively.

16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below? 

(i) Volume: 3x² – 12x

(ii) Volume: 12ky² + 8ky –20k

Answers:

(i) Volume: 3x² – 12x

3x² – 12x = 3x(x – 4)

Volume of cuboid = Length × Breadth × Height

Possible expressions are:

Length = 3, breadth = x and height = x – 4.

(ii) Volume: 12ky² + 8ky –20k

12ky² + 8ky –20k = 4k(3y² + 2y – 5)

Now let us factorise 3y² + 2y – 5.

p + q = 2 and pq = 3(-5) = -15.

By trial and error, we get p = 5 and q = -3.

3y² + 2y – 5

= 3y² + (5 – 3)y – 5

= 3y² + 5y – 3y – 5

= y(3y + 5) – 1(3y + 5)

= (y – 1)(3y + 5)

Therefore,

12ky² + 8ky –20k = 4k(y – 1)(3y + 5)

Possible expressions are:

Length = 4k, breadth = y – 1 and height = 3y + 5.

Summary:

The possible expressions for the dimensions of the cuboids whose volume are (i) 3x² – 12x and (ii) 12ky² + 8ky – 20k are 3, x, (x – 4) and 4k, (y – 1), (3y + 5) respectively.

Important Problems from Old NCERT Textbook:

Exercise 2.3 Page 35 (Old Textbook):

1. Find the remainder when x³ + 3x² + 3x + 1 is divided by

(i) x + 1              
(ii) x – 1/2           
(iii) x          
(iv) x + π           
(v) 5 + 2x

Answers:

(i) x + 1             

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

x + 1 = 0

or, x = – 1

p(-1) = (-1)³ + 3(-1)² + 3(-1) + 1 = -1 + 3 – 3 + 1 = 0

Therefore, when x³ + 3x² + 3x + 1 is divided by x + 1the remainder = 0.

(ii) x – 1/2       

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

x – 1/2 = 0

or, x = 1/2

p(1/2) = (1/2)³ + 3(1/2)² + 3(1/2) + 1 = 1/8 + 3/4 + 3/2 + 1 = (1 + 6 + 12 + 8)/8 = 27/8

Therefore, when x³ + 3x² + 3x + 1 is divided by x – 1/2, the remainder is 27/8.

(iii) x

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

The root of x = 0 is 0.

p(0) = (0)³ + 3(0)² + 3(0) +1

= 0 + 0 + 0 + 1

= 1

Therefore, when x³ + 3x² + 3x + 1 is divided by x, the remainder is 1.

(iv) x + π

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

x + π = 0

or, x = – π.

p(-π) = (-π)³ + 3(-π)² + 3(-π) + 1

= -π³ + 3π² – 3π + 1

Therefore, when x³ + 3x² + 3x + 1 is divided by x + π, the remainder is -π³ + 3π² – 3π + 1.

(v) 5 + 2x

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

5 + 2x = 0 or x = -5/2

p(-5/2) = [((-5)/2)³ + 3((-5)/2)² + 3((-5)/2) + 1]

= [((-125)/8) + (75/4) + ((-15)/2) + 1]

= (-125 + 150 – 60 + 8)/8

= (-27)/8

Therefore, when x³ + 3x² + 3x + 1 is divided by 5 + 2x, the remainder is (-27)/8.

Summary: The remainder when x³ + 3x² + 3x + 1 is divided by (i) x + 1, (ii) x – 1/2, (iii) x, (iv) x + π, and (v) 5 + 2x respectively are 0, 27/8, 1, −π³ + 3π² – 3π + 1 and -27/8.

2. Find the remainder when x³ − ax² + 6x − a is divided by x – a.

Answer:

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

x – a = 0

 or, x = a

p(a) = a³ – a(a)² + 6(a) – a

= a³ – a³ + 5a

= 5a Therefore, when x³ − ax² + 6x − a is divided by x – a, the remainder is 5a.

3. Check whether 7 + 3x is a factor of 3x³ + 7x.

Answer:

By remainder theorem, if p(x) is divided by linear polynomial x – a, the remainder is p(a).

7 + 3x = 0

or, x = -7/3

p(-7/3) = 3(-7/3)³ + 7(-7/3)

= (-343)/9 – 49/3

= (-343-49×3)/9

= – 490/9 ≠ 0

Therefore, 7 + 3x is not a factor of 3x³ + 7x since the remainder = – 490/9 ≠ 0.

Extra Questions to Complement Solutions to NCERT Class 9 Mathematics Chapter 2 Polynomials:

(A) Multiple Choice Questions (MCQ):

1. A rectangle has length x units and breadth 4 units. The area of the rectangle is a polynomial of degree:

(A) 1
(B) 2
(C) 0
(D) Not a polynomial

Answer: (A) 1

Area of the rectangle = Length × Breadth = 4x, which is a polynomial of degree 1 (highest power of x is 1).

2. The degree of the polynomial 0 is:

(A) 1
(B) 0
(C) Undefined
(D) Infinity

Answer: (C) Undefined

3. Degree of the polynomial 4x⁴ + 0x³ + 0x⁵ + 5x + 7 is (NCERT Exemplar)

(A) 4
(B) 5
(C) 3
(D) 7

Answer: (A) 4

4x⁴ + 0x³ + 0x⁵ + 5x + 7 = 4x⁴ + 5x + 7 The highest power of x is 4. So, the degree is 4.

4. Which of the following is a polynomial?

(A) 1/x³
(B) √2x³
(C) x – 1/x
(D) √x
Answer: (B) √2x³

The exponents of the terms have to be whole numbers. Therefore, √2×3 is the only polynomial.

5. P(x) = x² + x + 1. Find the value of [P(0)]².

(A) 4
(B) 1
(C) 0
(D) 2

Answer: (B) 1

P(0) = 0² + 0 + 1 = 1 [P(0)]² = P(0) × P(0) = 1 × 1 = 1

6. If x – 1 perfectly divides x² + kx + x + 1, what is the value of k?

(A) -2
(B) -3
(C) 1
(D) -1

Answer: (B) -3

By Remainder Theorem, if x – 1 exactly divides p(x), then p(1) = 0.

p(x) = x² + kx + x + 1

or, p(1) = 1² + k.1 + 1 + 1 = 0 or, k = -3

7. What is the remainder when 2x² – 1 is divided by x?

(A) 1
(B) 2x² – 1
(C) -1
(D) 0

Answer: (C) -1

x = x – 0

Therefore, by Remainder Theorem p(0) = r.

p(x) = 2x² – 1

or, p(0) = – 1 = r

8. The value of 300² – 299² is:

(A) 499
(B) 301
(C) 599
(D) 1

Answer: (C) 599

Using the identity a² – b² = (a + b)(a – b) we get:

300² – 299² = (300 + 299)(300 – 299) = 599.1 = 599

9. Which of the following is a factor of (2x + 1)² – (2x – 1)²?

(A) 9x
(B) 4x
(C) 3x
(D) 10x

Answer: (B) 4x

Using the identity a² – b² = (a + b)(a – b) we get:

(2x + 1)² – (2x – 1)²

= (2x + 1 + 2x – 1)(2x + 1 – 2x + 1)

= 4x × 2

= 8x

4x is a factor of 8x.

10. Which of the following can be expressed as the sum of two cubes:

(A) (3x + 1)(4x² – 2x + 1)
(B) (2x + 1)(4x² – 2x + 1)
(C) (2x + 1)(4x² – 4x + 1)
(D) (x + 1)(4x² – 2x + 1)

Answer: (B) (2x + 1)(4x² – 2x + 1)

We know,

(x + y)(x² – xy + y²) = x³ + y³

Here x = 2x and y = 1

(2x + 1)(4x² – 2x + 1) = 8x³ + 1³ (Sum of two cubes)

11. If x = -y, which of the following is true:

(A) x³ – y³ – 3xy(x – y) = 0
(B) x³ – y³ + 3xy(x – y) = 0
(C) x³ + y³ + 3xy(x + y) = 0
(D) x³ + y³ – 3xy(x – y) = 0

Answer: (C) x³ + y³ + 3xy(x + y) = 0

x = -y

or, x + y = 0

or, (x + y)³ = 0

or, x³ + y³ + 3xy(x + y) = 0

12. The coefficient of x² in the expansion of (2x + 1)³ is:

(A) 12
(B) 6
(C) 9
(D) 3

Answer: (A) 12

(2x + 1)³

= (2x)³ + 3(2x)²(1) + 3(2x)(1)² + 1³

= 8x³ + 12x² + 6x + 1

13. Factorise x² – x – 12:

(A) (x + 1)(x – 12)
(B) (x + 3)(x – 4)
(C) (x – 3)(x – 4)
(D) (x – 3)(x + 4)

Answer: (B) (x + 3)(x – 4)

x² – x – 12

p + q = – 1 and pq = -12

By trial and error we get,

p = – 4 and q = 3

x² – x – 12

= x² +(-4 + 3)x – 12

= x² – 4x + 3x – 12

= x(x – 4) + 3(x – 4) = (x + 3)(x – 4)

14. Find the value of (3x+3y)³/(x+y)³

(A) 9
(B) 8
(C) 27
(D) Undeterminable

Answer: (C) 27

(3x+3y)³/(x+y)³ =[3(x+y)]³/(x+y)³ = 3³ (x+y)³/(x+y)³ = 27

15. Find the value of 1/102³ without actually multiplying:

(A) 1/1000000
(B) 1/1001208
(C) 1/1061208
(D) 1/1041208

102³ = (100 + 2)³ = (100)³ + 3(100)²(2) + 3(100)(2)² + 2³

= 1000000 + 60000 + 1200 + 8

= 1061208

(B) Short Answer Type Questions:

Is x² – 3x + 1 a multiple of x – 1/2?

Answer:

p(x) = x² – 3x + 1

p(1/2) = (1/2)² – 3(1/2) + 1

= 1/4 – 3/2 + 1

= (1-6+4)/4

= (-1)/4

Since p(1/2) ≠ 0, there is a remainder when x² – 3x + 1 is divided by x – 1/2.

We can say that x² – 3x + 1 is not a multiple of x – 1/2.

2. Factorise: p³ + 6 + 12/p³ + 8/p⁶

Answer:

p³ + 6 + 12/p³ + 8/p⁶

= p³ + 3p²(2/p²) + 3p(2/p²)² + (2/p²)³

= (p3 + 2/p²)² [Factorised]

3. Express as the sum of two cubes and factorise: 3√3a³ + 3√3b³

Answer:

3√3a³ + 3√3b³

= (√3a)³ + (√3b)³ (Expressed as the sum of two cubes)

= (√3a + √3b)[(√3a)² – (√3a)(√3b) + (√3b)²]

= (√3a + √3b)(3a² – 3ab + 3b²)

= 3√3 (a + b)(a² – ab + b²) [Factorised]

4. Without finding the cubes, factorise:

(x – y)³ + (y – z)³ + (z – x)³

Answer:

We use identity x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)

Here, x = x – y, y = y – z, z = z – x

Here, (x – y) + (y – z) + (z – x) = 0

Therefore, (x – y)³ + (y – z)³ + (z – x)³ – 3(x – y)(y – z)(z – x) = 0 or, (x – y)³ + (y – z)³ + (z – x)³ = 3(x – y)(y – z)(z – x) (Factorised)

5. Express the following as the sum of two squares:

(p + 1)³ – (p – 1)³

= p³ + 3p²(1) + 3p(1)² + 1³ – (p³ – 3p²(1) + 3p(1)² – 1³)

= p³ + 3p² + 3p + 1 – p³ + 3p² – 3p + 1

= 6p² + 2

= (√6p)² + (√2)² [Sum of two squares]

6. Express the following as a cube:

(1 – x)³ + (1 – y)³ – 3(x + y – 2)(1 – x)(1 – y)

Answer:

(1 – x)³ + (1 – y)³ – 3(x + y – 2)(1 – x)(1 – y)

= (1 – x)³ + (1 – y)³ + 3(1 – x)(1 – y)(2 – x – y)

= (1 – x)³ + (1 – y)³ + 3(1 – x)(1 – y)[(1 – x) + (1 – y)]

We use the identity x³ + y³ + 3xy(x + y) = (x + y)³.

Here, x = 1 – x, y = 1 – y.

(1 – x)³ + (1 – y)³ + 3(1 – x)(1 – y)[(1 – x) + (1 – y)]

= (1 – x + 1 – y)³ = (2 – x – y)³ [Expressed as a cube)

7. Simplify the expression (3x³-24)/(x-2) where x ≠ 2.

Answer:

(3x³-24)/(x-2)

= (3(x³-8))/(x-2)

= (3(x-2)(x²+x.2+ 2²))/(x-2)

= 3(x² + 2x + 4)

8. Simplify the expression: (x²+x-6)/(x²+5x+6) where x≠-2, -3.

Answer:

(x²+x-6)/(x²+5x+6)

For x² + x – 6 we get:

p + q = 1 and pq = -1 × 6

By trial and error we get p = 3, q = -2.

For x² + 5x + 6 we get:

p + q = 5, pq = 1 × 6

By trial and error we get p = 3, q = 2.

(x²+x-6)/(x²+5x+6)

= (x²+(3-2)x-6)/(x²+(3+2)x+6)

= (x²+3x-2x-6)/(x²+3x+2x+6)

= (x(x+3)-2(x+3))/(x(x+3)+2(x+3))

= (x+3)(x-2)/(x+3)(x+2)

= (x-2)/(x+2) (Answer)

9. Find the value of x³ + y³ – 27xy + 8, when x + y = – 9.

Answer:

x³ + y³ – 27xy + 8

= x³ + y³ + 3xy(-9) + 8

= x³ + y³ + 3xy(x + y) + 8 [Since x + y = – 9]

= (x + y)³ + 8

= (-9)³ + 8

= -729 + 8 = -721 (Answer)

10. If y + 1 = x, find 2y³ + 6y² + 6y + 54 in terms of x.

Answer:

2y³ + 6y² + 6y + 54

= 2(y³ + 3y² + 3y + 27)

= 2(y³ + 3y².1 + 3y.1² + 1³ + 26)

= 2(y + 1)³ + 2 × 26

= 2(y + 1)³ + 52

= 2x³ + 52 (Answer)

(C) Long Answer Type Questions:

1. If a + b = 4 and ab = 2, find the value of (1/a + 1/b)³ – 1/a³ – 1/b³ .

Answer:

(1/a + 1/b)³ – 1/a³ – 1/b³ .

= 1/a³ + 1/b³ + 3(1/a)( 1/b)(1/a + 1/b) – 1/a³ – 1/b³

= (3/ab)(1/a + 1/b)

= 3/ab((a + b)/ab)

= (3(a + b))/(a² b² )

Putting a + b = 4 and ab = 2 we get:

(3(a + b))/(a² b²) = (3 × 4 )/4 = 3

Therefore,

(1/a + 1/b)³ – 1/a³ – 1/b³ = 3

2. If x + 1/x = 3, find the value of (x⁶+1+3x⁴+3x²)/x³ .

Answer:

(x⁶+1+3x⁴+3x²)/x³

= x⁶/x³ + 1/x³ +3x⁴/x³ + 3x²/x³

= x³ + 1/x³ + 3x + 3/x

= x³ + 1/x³ + 3×1/x (x + 1/x)

= (x + 1/x)³

= 3³

= 27

3. If x – 1 is a factor of x² – px – p and x – 2 is a factor of x² + qx + 2, find the value of p + q.

Answer:

p(x) = x² – px – p

By remainder theorem,

p(1) = 1² – p(1) – p = 0

or, 2p = 1

or, p = 1/2

q(x) = x² + qx + 2

By remainder theorem,

q(2) = 2² + q(2) + 2 = 0

or, 2q = – 6

or, q = -3

Therefore, p + q = 1/2 – 3 = -5/2

4. Express the following as the sum of squares:

2(x – 1)² + 2(y – 1)² + 2(z – 1)² 2(x – 1)(y – 1) + 2(y – 1)(z – 1) + 2 (z – 1)(x – 1)

Answer:

2(x – 1)² + 2(y – 1)² + 2(z – 1)² + 2(x – 1)(y – 1) + 2(y – 1)(z – 1) + 2 (z – 1)(x – 1)

= (x – 1)² + 2(x – 1)(y – 1) + (y – 1)² + (y – 1)² + 2(y – 1)(z – 1) + (z – 1)² + (z – 1)² + 2 (z – 1)(x – 1) + (x – 1)²

Using identity a² + 2ab + b² = (a + b)² we get:

= ( x – 1 + y – 1)² + (y – 1 + z – 1)² + (z – 1 + x – 1)² = (x + y – 2)² + (y + z – 2)² + (z + x – 2)² [Expressed as the sum of three squares]

(D) Fill in the Blanks:

(a) A polynomial of degree __________ is called a linear polynomial.

(b) A polynomial with three terms is called a _________.

(c) In the polynomial a₀ + a₁x + a₂x², if a₀ = a₁ = a₂ = 0 then the polynomial is a __________ polynomial.

(d) The polynomial x² + xy + z² has __________ variables.

(e) The expression (x – 2)(x² + 5x + 6) has __________ factors.

Answers:

(a) A polynomial of degree 1 is called a linear polynomial.

(b) A polynomial with three terms is called a trinomial.

(c) In the polynomial a₀ + a₁x + a₂x², if a₀ = a₁ = a₂ = 0 then the polynomial is a zero polynomial.

(d) The polynomial x² + xy + z² has three variables.

(e) The expression (x – 2)(x² + 5x + 6) has three factors.

++++++++++++++

Frequently Asked Questions (FAQs) on NCERT Solutions to Class 9 Mathematics Chapter 2 Polynomials: